Anleitung zu Versuch 01: Analyse von Versuchsdaten und Simulationsdaten mit Excel

1.1 Erzeugung von Daten mit LTSPICE

Starten Sie LTSPICE und richten Sie es ein. Tools->Control Panel->Waveforms: Data trace width (Plot thick lines) Tools->Control Panel->Drafting Options: Pen thickness (Plot thick lines) Tools->Color Preferences ->Waveform->Background R,G,B 255,255,255 weiss. Erstellen und simulieren Sie folgende Schaltung. File -> New Schematic Bauelemente plazieren: Edit -> Component->Voltage Edit -> Place GND Edit -> Resistor Edit -> Draw Wire Setzen der Werte Rechts Click auf dem Wert eines Bauteils oder über der Spannungsquelle erlaubt die Eingabe der Werte. Simulation: Simulate->Edit Simulation Cmd DC Sweep: Name of 1st Source: V1; Start value: -2 Stop Value:2 Increment: 0.1 Simulate->Run

Man erzeugt Kurven durch Mausrechtsklick und AddTrace oder durch Mausklick im Schaltplan. Den Schaltplan oder die Kurve können Sie mit

• Tools-> Copy Bitmap to Clipboard

in die Zwischenablage kopieren und dann hier einfügen.

Kopieren Sie hier vom Clipboard ( < Strg > v ) einen Screenshot (< Alt > < Druck > ).

Remove


Dokumentieren Sie die SPICE Netzliste

• Menue View -> SPICE Netlist

Fügen Sie die Netzliste hier ein und ergänzen Sie Kommentare.

Speichern Sie den Schaltplan mit einem geeigneten Namen ab: Gruppe, Name, Kennlinieart. Nun exportieren Sie die Simulationswerte:

• File->Export->I(R1)

1.2. Darstellung der Werte in Excel

1.3. Analyse der Werte

1. Darstellung einer parametrisierten Gleichung
   Als erstes fügen Sie ein Feld für den Parameter R ein und tragen den Wert 300Ω ein.

   	A	B	C
   1	Parameter	Wert	Einheit
   2	R	300	Ω

   In der Wertetabelle erzeugen Sie nun eine neue Spalte mit den Gleichungswerten.

   	A	B	C
   5	v1	I(R1)	I(Gleichung)
   6	-2.00	-1.00E-02	=A6/$B$2

   Dabei fügen Sie die Gleichung =A6/$B$2 in die Zelle C6 ein.
   Die vorangestellten $ Zeichen drücken einen absoluten Bezug aus. Wenn Sie die Zelle kopieren bleibt dieser Wert gleich, während sich der relative Bezug A6 ändert.

   	A	B	C
   25	1.80	9.00E-03	=A25/$B$2
   26	2.00	1.00E-02	=A26/$B$2

2. Regressionsgerade
   Wählen Sie die erste Kurve im Diagramm aus. Mit der rechten Maustaste können Sie das Menü:

   • Trendlinie hinzufügen

   auswählen.
   Da eine lineare Beziehung gegeben ist wählen Sie den Typ

   • linear

   aus. Aktivieren Sie die Option

   • Formel im Diagramm anzeigen und Bestimmtheitsmaß darstellen.

   Das Bestimmtheitsmaß r² gibt die Abweichung der gemessenen oder simulierten Wertepaaren x_ni,y_ni von den geschätzten(berechneten) Wertepaaren x_mi,y_mi an. Im Idealfall ist das Bestimmtheitsmaß 1.
   Das Bestimmtheitsmaß ist definiert [1] als
   \( r^2 = \frac{ \sum{(y_{ni} - \overline{y_m})^2}} { \sum{(y_{mi} - \overline{y_m})^2}} \)
   
   Dokumentieren Sie die Gleichung.
   
   und das Bestimmtheitsmaß
   
   
3. Kurven Fitting
   In der Elektrotechnik sind Gleichungen für das Verhalten von Bauelementen vorgegeben und nur die Parameter müssen bestimmt werden. Als Maß für die Qualität des Kurven Fittings wird die Summe der Fehlerquadrate angenommen. Man bestimmt dabei:

   \( F = \sum{(y_i - f(x_i))^2} \)

   y_i sind die gemessenen Werte und f(x_i) sind die berechneten Werte. Durch geeignete Wahl der Gleichungsparameter kann man den Fehler minimieren (F→0).
   Erstellen Sie eine Spalte mit dem Fehler zwischen den gemessenen Werten und den berechneten Werten.

   	A	B	C	D
   5	v1	I(R1)	I(Gleichung)	Fehlerquadrate
   6	-2.00	-1.00E-02	-0.0666667	=(C6-B6)*(c6-B6)

   Bestimmen Sie den gesamten Fehler aus der Summe der Fehlerquadrate (Zellen A,B 4) und dokumentieren Sie den Fehler.
   Beobachten Sie die Veränderung des Fehlers, wenn Sie den Parameter R ändern. Geben Sie den Fehler für verschiedene Werte R an.
   
   Fügen Sie hier eine Bildschirmkopie des Excelblattes ein:
   Kopieren Sie hier vom Clipboard ( < Strg > v ) einen Screenshot (< Alt > < Druck > ).
   
   Remove
   
   
4. Optional Optimierung
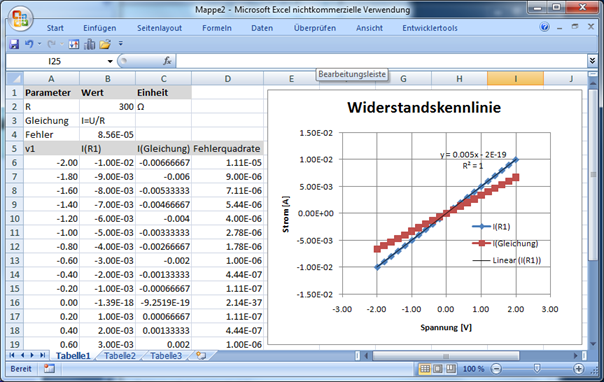
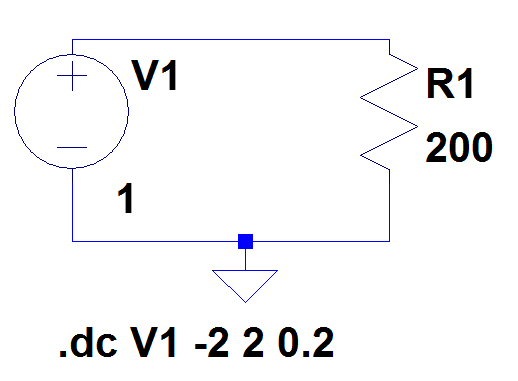
   Man kann in Excel den Parameter R manuell iterativ optimieren, damit die Summe der Fehlerquadrate minimal wird. Dazu braucht man die Information, wie sich bei einer Änderung des Parameters R der Fehler ändert.
   Deshalb fügt man zwei neue Spalten ein:
   In Spalte E berechnet man den Strom wenn R ($B$2) geändert wird 0.999*$B$2.

   	A	B	C	D	E	F
   5	v1	I(R1)	I(Gleichung)	Fehlerquadrate	I(R1*0.999)	Fehler(R1*0.999
   6	-2.00	-1.00E-02	-0.0666667	=(C6-B6)*(C6-B6)	=A6/(0.999*$B$2)	=(E6-B6)*(E6-B6)

   Die neue Fehlersumme wird in Zelle E,F4 mit Namen und Wert eingetragen.
   Der neue Widerstand wird nun in Zelle E,F2 mit Namen und Wert berechnet nach:
   R_neu = R_alt (1-SummeFehler/(SummeFehler-SummeFehlerneu)*0.001) = B2*(1-0.001*B4/(B4-F4))
   
   Beobachten Sie wie viele Schritte Sie brauchen um vom Startwert 300Ω zum Zielwert 200 Ω kommen, indem Sie den neuen Widerstandswert immer wieder in die Zelle B2 kopieren.

Plain

Plain1

Plain2

Info:

Read Data