Elektronik 3

09 MOSFET

Prof. Dr. Jörg Vollrath

08 MOSFET

Video 09 MOSEFT

Länge: 01:06:27

0:0:0 Willkommen

0:0:8 MOSFET Versuch

0:1:8 Gehäuse DIL package

0:3:56 Transistorgleichung

0:6:33 Wurzel des Strome sist eine Geradengleichung

0:10:31 Ausgangskennlinie und λ

0:16:41 Kapazitäten des MOSFETs

0:22:25 Transistorentwicklung

0:28:31 NMOS LTSPICE Modell

0:32:17 Level 1 Modell

0:36:28 Unterschwellspannungsbereich

0:39:34 Transistor als Verstärker

0:43:38 Verstärkerkennlinie

0:49:59 Kleinsignalgleichungen

0:53:16 Wiederholung Diode

0:54:19 MOSFET Kleinsignalgleichung

0:57:5 Steilheit, Übertragungsleitwert gm

1:0:22 Ausgnagsleitwert gd

1:3:53 Zusammenfassung

1:6:56 Beispiel Rechnung Arbeitspunkt

1:10:58 Berechnung UDS

1:12:31 Kleinsignalrechnung

1:14:6 Kleinsignalersatzschaltbild

1:16:14 gm

1:17:9 gd

1:18:47 gd und R

1:20:11 Grösserer Widerstand R

Heute

MOSFET

Kapazitäten
Modelle
Transistorentwicklung
Der MOSFET als Verstärker: Kleinsignalverhalten

Elektronische Schaltungstechnik, Reinhold: Kapitel 6, S. 102-124
Microelectronic, Jaeger: Chapter 4, page: 145-216

Kapazitäten sind in einem MOSFET vorhanden und bestimmen das Frequenzverhalten von Schaltungen.
Sie begrenzen die maximal mögliche Signalfrequenz bei der ein Eingangssignal noch verstärkt werden kann.

Es werden SPICE Modelle vorgestellt, damit man mit Simulationen Rechnungen überprüfen kann.
Dabei muss man beachten, dass ein Modell nur das wiedergeben kann, was auch im Modell abgebildet ist.
Simulieren kann man das Transistorverhalten auch bei sehr grossen Leistungen, bei denen ein reales Bauteil durch thermische Belastung oder hohe Feldstärken schon zerstört werden würde.

Da es auch Schaltungen gibt die im Unterschwellspannungsbereich des Transistors arbeiten wird dieser als Erweiterung der MOSFET Transistorgleichung vorgestellt.

Betrachtet man die Transistorentwicklung zeigt sich eine Leistungssteigerung des Transistors mit immer kleineren Strukturgrößen. Kapazitäten werden kleiner, die Versorgungsspannung nimmt ab, die Bandbreite von Schaltungen nimmt zu und der Leistungsverbrauch bei gleicher Frequenz ab.
Während in den letzten 50 Jahren die Strukturen regelmäßig kleiner wurden, kommt man langsam an eine physikalische Grenze durch die Atomgröße, durch Dotierung, die Leistungsdichte und die Fertigungstoleranzen.

Eine Betrachtung eines einfachen Verstärkers zeigt, dass zwischen Eingangsspannung und Ausgangsspannung eine quadratische Beziehung besteht.
Um das Verständnis und die Rechnung zu erleichtern wird eine Linearisierung der Gleichung in einem Arbeitspunkt durchgeführt. Die Ausgangsspannung hängt dann näherungsweise linear von der Eingangsspannung ab. Es wird ein Kleinsignalersatzschaltbild entwickelt.
Linearisierung ist ein bewährtes Mittel, um nichtlineare Gleichungen näherungsweise zu lösen. Die Linearisierung erfordert immer eine 2 stufige Rechnung. Erst wird ein Arbeitspunkt bestimmt. Dann wird ein Verhalten, zum Beispiel eine Verstärkung, für diesen Arbeitspunkt berechnet.
Lineare Gleichungen helfen beim Verständnis und bei der Optimierung von Schaltungen.

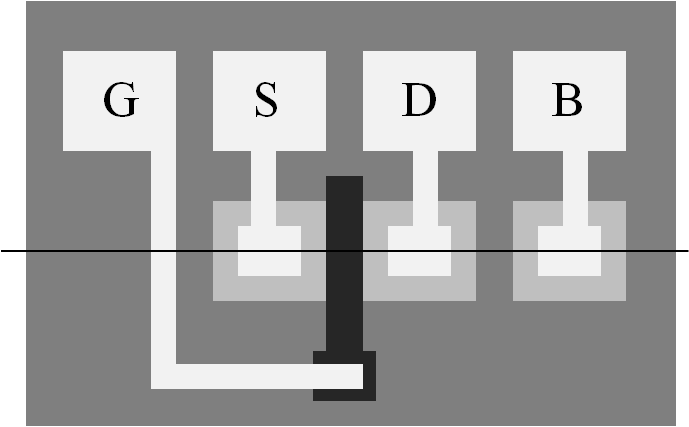
Kapazitäten elektronischer Bauelemente

Limit high-frequency performance of the electronic device they are associated with.
Limit switching speed of circuits in logic applications
Limit frequency at which useful amplification can be obtained in amplifiers.
MOSFET capacitances depend on region of operation and are non-linear functions of voltages at device terminals.

\( C_{GS}= C_{GD} = 0.5 \cdot C_{ox} \)

\( C_{ox}= \epsilon_{ox} \frac{WL}{d_{ox}} \)

W: Kanalweite, L: Kanallänge, d_ox = t_ox: Oxiddicke

NMOSFET SPICE Modell

Typische Werte
\( KP = 20..50 \mu A /V^2 \)
KP = K_N = 2 · β
γ
λ = 0
\( V_{th} = 1V \)
\( \mu_{n}, \mu_{p} = 500 ... 200 \frac{cm^2}{Vs} \)
\( 2 \Phi_{F} = 0.6V \)
\( C_{GD0} = C_{GS0} = 0 F \)
\( C_{GB0} =C_{JSW} = 0 F \)
\( d_{ox} = 100nm \)

LEVEL = 1 einfache Gleichungen

SPICE MOS Modell

.model AO6407 VDMOS(pchan Rg=3 Rd=14m Rs=10m 
+ Vto=-.8 Kp=32 Cgdmax=.5n Cgdmin=.07n Cgs=.9n 
+ Cjo=.26n Is=26p Rb=17m mfg=Alpha_&_Omega 
+ Vds=-20 Ron=34m Qg=13n)

.MODEL N_1u NMOS LEVEL  = 3                  
+ TOX  = 200E-10 NSUB = 1E17    GAMMA = 0.5          
+ PHI  = 0.7     VTO  = 0.8     DELTA = 3.0         
+ UO   = 650     ETA  = 3.0E-6  THETA = 0.1          
+ KP   = 120E-6  VMAX = 1E5     KAPPA = 0.3                
+ RSH  = 0       NFS  = 1E12    TPG   = 1                  
+ XJ   = 500E-9  LD   = 100E-9                 
+ CGDO = 200E-12 CGSO = 200E-12 CGBO  = 1E-10              
+ CJ   = 400E-6  PB   = 1       MJ    = 0.5           
+ CJSW = 300E-12 MJSW = 0.5                                  
*

Weitere Modelle finden sich im Internet:

Baker: 1 µm MOSFET model, 50 nm MOSFET model, cmosedu_models.txt
Sedra Smith Level=1 5 µm, 0.5 µm: sedra_lib.lib
Allen, Holberg Level=3 0.8 µm: Holberg.txt
TSMC 0.25um CMOS MOSFETs (level 3) t14y_tsmc_025_level3.lib from MOSIS .
ALD1101, ALD1102, David A. Johns University of Toronto

CD4007

.model CD4007N NMOS(LEVEL=1 KP=500u VT0=1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)
.model CD4007P PMOS(LEVEL=1 KP=500u VT0=-1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)

ALD1106, ALD1107

.model ALD1106N NMOS(LEVEL=1 KP=0.48m VT0=0.7 LAMBDA=0.018 CGDO=100n CGSO=100n)
.model ALD1107P PMOS(LEVEL=1 KP=0.2m VT0=-0.7 LAMBDA=0.018 CGDO=100n CGSO=100n)

ALD1101, ALD1102

* ALD ALD1101 (NMOS) and ALD 1102 (NMOS) model
* This model was extracted from measurements.
* The model is correct only for W = 1738 um and L = 1 um.
* The device size above doesn't represent the actual device size.

* NMOS hand analysis values: Vtn = 0.71 V; UnCox(W/L) = 4.5 mA/V^2 ; VA = 80 V;
.MODEL ALD1101 NMOS LEVEL = 2 UO = 12.72 VTO = 0.6766 NFS = 1.154E12 TOX = 1E-08 NSUB = 3.892E17 UCRIT = 4.582E05 UEXP = 0.07025 VMAX = 6363 RS = 9.491 RD = 5.659 XJ = 4.787E-09 LD = 0 DELTA = 1E-12 NEFF = 0.8345 NSS = -3.801 CGSO = 1.15E-9 CGDO = 1.15E-9 CGBO = 0 CBD = 0 CBS = 0 CJ = 0 MJ = 0.5 CJSW = 0 MJSW = 0.6057 IS = 1.0E-14 PB = 0.8 FC = 0.5 NEFF=5

* PMOS hand analysis values: Vtn = -0.65 V; UpCox(W/L) = 2.10 mA/V^2 ; VA = -19 V;
.MODEL ALD1102 PMOS LEVEL = 2 UO = 5.536 VTO = -0.6093 NFS = 3.602E12 TOX = 1E-08 NSUB = 4.046E16 UCRIT = 8.118E04 UEXP = 0.1647 VMAX = 1399 RS = 9.249 RD = 38.77 XJ = 4.443E-09 LD = 0 DELTA = 8828 NEFF = 2.145 NSS = -8.793 CGSO = 1.15E-9 CGDO = 1.15E-9 CGBO = 0 CBD = 0 CBS = 0 CJ = 0 MJ = 0.5 CJSW = 0 MJSW = 0.33 IS = 1E-14 PB = 0.8 FC = 0.5

CMOS 1µm models (Holberg)

** Holberg, p 337 Table6.6-1
.model NMOS1 NMOS(LEVEL=1 VT0=0.70 KP = 110U GAMMA = 0.4 LAMBDA = 0.04 PHI = 0.7 MJ = 0.5
+ MJSW = 0.38 CGBO =700P CGSO=220P CGDO = 220P CJ = 770U CJSW = 380P LD = 0.016U TOX= 14N) 
.model PMOS1 PMOS (LEVEL=1 VT0 = -0.70 KP = 50U GAMMA = 0.57 LAMBDA = 0.05 PHI = 0.8 MJ = 0.5
+ MJSW = 0.35 CGBO =700P CGSO=220P CGDO = 220P CJ = 560U CJSW = 350P LD = 0.014U TOX= 14N)

Transistorentwicklung

Transistoren werden immer kleiner
Was bedeutet das für die elektrischen Eigenschaften.

Modelle werden komplizierter
Spannungen werden kleiner
Eingangskapazitäten werden kleiner
Leistungsverbrauch nimmt ab.
Höhere Frequenzen möglich

MOSFETs finden immer mehr Anwendungen

1970 8 \( \mu m \)
1980 2 \( \mu m \)
1990 0.5 \( \mu m \)
2000 130 \( nm \)
2010 40 \( nm \)
2013 22 \( nm \)
2015 14 \( nm \)

Jahr und Strukturgröße

Unterschwellspannungskennlinie

Subthreshold region
Weak Inversion
Übertragungskennlinie
Exponentieller Zusammenhang zwischen Strom und Spannung

Weitere Transistormodelle
LEVEL=3…40

\( I_{DW}=I_{D0} \cdot e^{\frac{U_{GS}-U_{th}}{nU_T}} \left( 1- e^{-\frac{U_{DS}}{U_T}}\right) \)

MOSFET als Verstärker: Das Prinzip

R_D: Bestimmt die Ausgangsspannung Ua
U_a(t)= U_DD-I_DS(t)·R_D
\( I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) \)
Die Eingangsspannung erzeugt eine Stromänderung,
die mit R_D in eine Ausgangsspannung umgesetzt wird.

MOSFET als Verstärker: Die Kennlinie

R_D: Bestimmt die Ausgangsspannung Ua

\( U_{a}= U_{DD} - \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) \cdot R_{D} \)
Die Ausgangsspannung U_a hängt nicht linear mit der Eingangsspannung U_GS zusammen.

Die Eingangsspannung erzeugt eine Stromänderung,
die mit R_D in eine Ausgangsspannung umgesetzt wird.

\( U_{th} = 1 V \), \( V_{DD} = 9 V\), \( \beta = 0.12 mAV^{-2} \),
\( \lambda = 0.01 V^{-1} \), \( R_{Load} = 10 k\Omega \)
Arbeitspunkt: U_GS=2.5V
\( \Delta U_{GS} = 1V (+-0.5V) \)
\( \Delta I_{DS} = 0.5 mA - 0.1 mA = - 0.4 mA \)
\( \Delta U_{DS} = 4 V - 8 V = -4 V \)
Spannngsverstärkung: VU = -4V/1V = -4

Großsignalverhalten und Kleinsignalverhalten

Großsignalverhalten

Kleinsignalverhalten

Kleine Signale
Näherung durch Tangente (Ableitung)

Kleinsignalersatzschaltbild
AC Analysis

Kleinsignalverhalten

Steilheit: g_m

Sättigung

\( g_m = \frac{2 I_{DS}}{U_{GS}-U_{th}} \simeq 2 \sqrt{\beta \cdot IDS} \)

Große Steilheit für großen Strom

Ausgangsleitwert: g_d

\( g_d = \beta \left( U_{GS}-U_{th} \right)^2 \lambda = \frac{I_{DS}\lambda}{1+\lambda U_{DS}} \simeq I_{DS} \lambda \)

Spannungsverstärkung: V_u

\( v_u = \frac{u_{DS}}{u_{GS}} = \frac{- g_m \cdot u_{GS}}{g_d \cdot u_{GS}} = - \frac{g_m}{g_d} \)
\( v_u = - \frac{2 I_{DS}}{(U_{GS}-U_{th}) I_{DS} \lambda} = - \frac{2}{(U_{GS}-U_{th}) \lambda} \)

Quelle Vollrath

MOSFET Elektronik 3 Rückblick, Heute

NFET, PFET
Unterschwellspannungsbereich (Subthreshold region)
Kapazitäten
Transistorentwicklung
Modell
SPICE: spannungsgesteuerte Stromquelle, Dioden, Kapazitäten
Kleinsignal
Steilheit: Stromänderung pro Eingangsspannungsänderung
Ausgangsleitwert

Als Nächstes:

10 MOSFET

Frequenzverhalten
Schalter
Ein realer MOSFET
Bipolartransistor