Elektronik 3

11 MOSFET

Prof. Dr. Jörg Vollrath

10 MOSFET

Video 11 MOSEFT

Länge: 01:06:27

0:0:0 Rückblick und Heute

0:1:18 MOSFET als Schalter

0:5:6 Arbeitsbereich Linearbereich

0:7:45 RDSon

0:13:20 ALD1116 Datenblatt

0:16:39 Features

0:19:20 Absolute maximum ratings

0:20:10 Vt

0:23:16 GIS gm mho=S

0:25:30 Übertragungskennlinie und Ausgangskennlinie

0:30:32 KP = KN = 2 β

0:32:36 λ

0:34:40 CIS = Cox

0:37:28 P Kanal MOSFET Mikroskopbild

0:41:0 PFET auf dem Breadboard

0:43:30 Messschaltung

0:44:42 Datenblatt Kennlinien

0:46:48 Transistorgehäuse und Anschlüsse

0:47:22 Messaufbau

0:49:53 Arbitrary waveform generator AWG Funktionsgenerator

0:51:37 Oszilloskopbild

0:53:15 Mathematikkanal definieren.

0:53:43 xy Darstellung

0:57:10 Ausgangskennlinie

0:58:12 MOSFET Parameterextraktion

1:2:17 Trendlinie und Messung y = IDS x = UGS

1:5:30 JFET low noise, wenig Rauschen

1:10:42 Leistungs-MOSFET Drain unten

Rückblick und Heute

MOSFET:

MOSFET als Verstärker: Spannungsverstärkung, Frequenzgang
MOSFET als Schalter: Ausgangswiderstand

MOSFET Datenblatt
MOSFET Messung
JFET
Leistungs-MOSFET

Elektronische Schaltungstechnik, Reinhold: Kapitel 4, S. 65-95
Microelectronic, Jaeger: Chapter 5, page: 217-284

MOSFET als Schalter

Der MOSFET schaltet den Strom für R_D an oder aus.
In welchem Arbeitsbereich arbeitet der Transistor?
Wie groß ist der Strom durch den Transistor, die Spannung und Verlustleistung im eingeschalteten Zustand?

Verstaerker03.asc

Version 4
SHEET 1 880 680
WIRE 256 80 256 64
WIRE 256 176 256 160
WIRE 256 176 304 176
WIRE 256 192 256 176
WIRE 352 240 256 240
WIRE 208 272 176 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 256 304 256 288
FLAG 256 304 0
FLAG 176 272 UGS
FLAG 304 176 UA
FLAG 256 64 VDD
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMBOL res 240 64 R0
SYMATTR InstName RD
SYMATTR Value ""

MOSFET als Schalter

Der MOSFET schaltet den Strom für R_D an oder aus.
In welchem Arbeitsbereich arbeitet der Transistor?

$U_{DS} \lt U_{GS}-U_{th}$ Linearbereich
R_on

$I_{DS} = \beta \left( 2 \left(U_{GS}-U_{th}\right)U_{DS}-U_{DS}^2\right)$

$R_{on} = R_{DS} = \left[\frac{dI_{DS}}{dU_{DS}}\right]^{-1} = \frac{1}{\beta 2 \left(U_{GS}-U_{th}-U_{DS}\right)}$
Für kleine U_DS gilt:

$R_{on} = \frac{1}{\beta 2 \left(U_{GS}-U_{th}\right)}$

Verstaerker03a.asc

Version 4
SHEET 1 880 680
WIRE 256 80 256 64
WIRE 256 176 256 160
WIRE 256 176 336 176
WIRE 256 192 256 176
WIRE 352 240 256 240
WIRE 208 272 176 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 256 304 256 288
FLAG 256 304 0
FLAG 176 272 UGS
FLAG 336 176 UA
FLAG 256 64 VDD
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMBOL res 240 64 R0
SYMATTR InstName RD
SYMATTR Value ""

MOSFET Model Parameter

NMOS Transistor ALD-1116: Für einen Strom I_DS=10mA finden Sie die Werte für V_thN, K_P,

$\lambda$ , C_GS und C_GD aus dem Datenblatt.

Google Suche: NMOS Transistor ALD-1116
www.aldinc.com/pdf/ALD1106.pdf
Lokale Kopie

T=25°C, V_DS= 5 V
V_thN = 0.7 V
I_DS= 4.8 mA
G_IS= 1.8 mS = g_m
G_OS= 200 uS = g_d
C_ISS=1 pF

$\lambda = \frac{g_d}{I_{DS}} = \frac{G_{OS}}{I_{DS}} = \frac{0.2 mS}{10 mA} = 0.02 V^{-1}$

$K_N$ vom on drain current

$I_{DS(ON)}$ :

$K_N = \frac{2 \cdot I_{DS(ON)}}{\left( U_{GS} - U_{th}\right)^{2}}$

$K_N = \frac{2 \cdot 4.8 mA }{\left( 5 V - 0.7 V \right)^{2}} = 0.5 \frac{mA}{V^{2}}$

$C_{ISS} = C_{GS} + C_{GD} \rightarrow C_{GS} = 1 pF;$

$g_m = 1.8 mS; f_t = \frac{g_m}{2 \pi C_{ISS}} = 300 MHz,v_u = -\frac{G_{IS}}{G_{OS}} = -9$

P-Channel Enhancement-Mode MOSFET Transistors

Part Number	$V(BR)_{DSS}$ Min (V)	$V_{GS}(th)$ (V)	$r_{DS}(on)$ Max $(\Omega)$	$I_D(on)$ Min (mA)	$C_{rss}$ Max(pF)	$t_{ON}$ Typ(ns)
3N163	-40	-2 to -5	250	-5	0.7	18

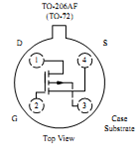
Quelle Datenblatt Quelle Vollrath

P-Channel Enhancement-Mode MOSFET Transistors 3N163

Features

Ultra-Low Input Leakage:
I_GS=0.02 pA Typ.
High Gate Breakdown Voltage: 125 V
Normally Off

Benefits

High Input Impedance Isolation
Minimize Handling ESD Problems
High Off Isolation without Power

Applications

Ultra-High Input Impedance Amplifier
Smoke Detectors
Electrometers
Analog Switching
Digital Switching

Quelle Datenblatt Siliconix 3N163

Datenblatt 3N163

Messaufbau 3N163

Source: GND, Drain: 100 Ω, AWG1, AWG2, Gate: AWG2, AWG1

Übertragungskennlinie

AWG1, Treppe 0..-10V, 50Hz, OSC1DC, VDD, 100 Ω
AWG2, Dreieck 0..-10V,250Hz, OSC3DC, VGS
OSC2DC, VDS Drainspannung, M1 = UOSC1DC - UOSC2DC
Kurve: x:OSC3DC y:M1

Ausgangskennlinie

AWG1, Treppe 0..-10V, 50Hz, OSC1DC, VGS
AWG2, Dreieck 0..-10V,250Hz, OSC3DC, VDD, 100 Ω
OSC2DC, VDS Drainspannung, M1=UDC3-UDC2
Kurve: x:DC2 y:M1

Schwellspannung: -4V
Verstärkung

VDD = -10 V, VGS = -5V+-110 mV, VDS = -1.82V +-440 mV, AV = 4

Messung 3N163

Sägezahn: -8V..0V
Amplitude 4V Offset -4V
Treppe:
Amplitude: 4V Offset: -6V
R=100Ohm, UGS=-6V, IDS=-2mA, UDS = 6V

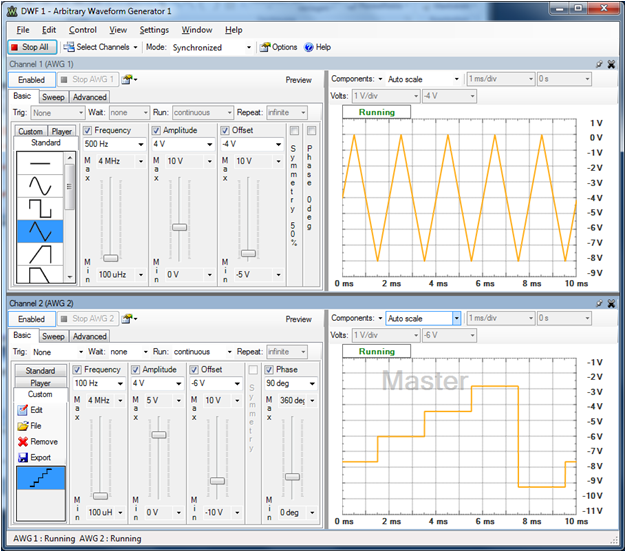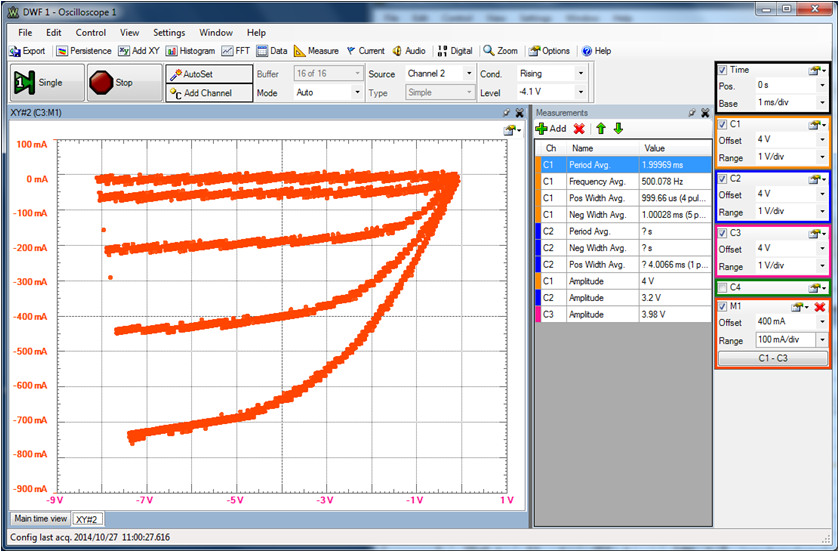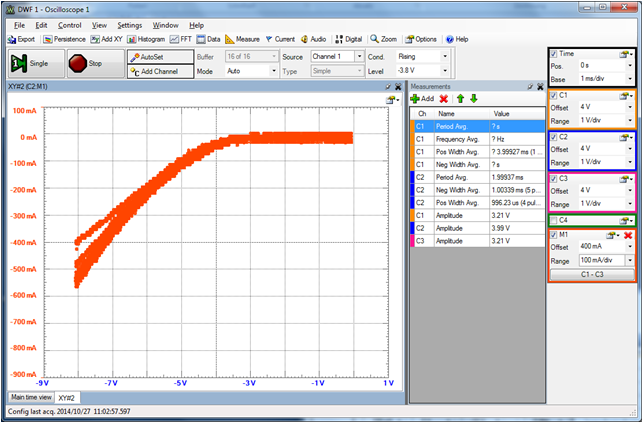
MOSFET Parameterextraktion

$I_{DS}= \cases{ 0 & \text{ für } U_{GS} \leq U_{th} \text{ Sperrbereich } \cr \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) & \text{ für } 0 \leq U_{GS} - U_{th} \lt U_{DS} \text{ Sättigung } \cr \beta \left( 2 \left( U_{GS}-U_{th} \right) U_{DS} - U_{DS}^2 \right) & \text{ für } 0\leq U_{GS} - U_{th} \geq U_{DS} \text{ Triodenbereich } }$

$\beta = \frac{\mu_{n} \epsilon_{ox}}{2d_{ox}} \frac{W}{L} = \frac{1}{2} \mu_{n} C_{ox}^{'} \frac{W}{L} = \frac{1}{2} K_{n}^{'} \frac{W}{L} = \frac{1}{2} K_{n}$

Sättigungsbereich:

$U_{GS} = const$ ;

$U_{DS1}, U_{DS2} \rightarrow \frac{I_{DS1}}{I_{DS2}} \rightarrow \lambda$

$U_{DS} = const$ ;

$U_{GS1}, U_{GS2} \rightarrow \frac{I_{DS1}}{I_{DS2}} \rightarrow U_{th}$

$\beta$

Funktion:

$y = \sqrt{I_{DS}} = \sqrt{\beta} \left( U_{GS} - U_{th} \right) \sqrt{\left( 1 + \lambda U_{DS} \right)}$

$y = \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{GS} - \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{th}$

$x = U_{GS}$ ,

$a = \sqrt{\beta \left( 1 + \lambda U_{DS} \right) }$ ,

$b = - \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{th} = - a \cdot U_{th}$

$y = ax + b$

1. Mathematische Methode:
Bei 2 Messungen bei gleicher Spannung U_GS und unterschiedlicher Spannnung U_DS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme λ.
Bei 2 Messungen bei gleicher Spannung U_DS und unterschiedlicher Spannnung U_GS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme U_th.
β kann man dann aus einer Messung durch einsetzen von I_DS, U_th, λ und U_GS berechnen.
2. Methode durch grafische Interpretation

Bei 2 Messungen bei gleicher Spannung U_GS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme λ. Trägt man die Wurzel des Stromes I_DS über der Gate-Source-Spannung auf ergibt sich eine Geradengleichung.
Aus der Steigung dieser Geraden und dem y-Achsenabschnitt bei x = U_GS0 ergeben sich U_th und bei kleinem λ und Vernachlässigung von λ U_DS gegenüber 1 dann β.

Junction Field-Effect Transistor JFET (SFET Sperrschicht FET)

Ugs [V]	Uds [V]
0	0

Much lower input current and much higher input impedance than the BJT.
In triode region, JFET is a voltage-controlled resistor:

$R_{CH} = \frac{\rho}{t} \frac{L}{W}$

$\rho$ = resistivity of channel
L = channel length
W = channel width between pn junction depletion regions
t = channel depth
Inherently a depletion-mode device

Leistungs MOSFET

Hohe Spannung U_DS

Niedriger R_DSon

DMOS, VMOS, HEXFET

Quelle: Wikipedia

Fragen: MOSFET

Wie sieht der Querschnitt eines MOSFETs aus?
Welche Anschlüsse hat der MOSFET?
Welche Typen von Feldeffekttransistoren gibt es?
Geben Sie die statische Gleichung eines MOSFETs an?
Wie kann man die Schwellspannung beeinflussen?
Wie sieht das Kleinsignalersatzschaltbild aus?

Gleichungen

$I_{DS}= \cases{ 0 & \text{ für } U_{GS} \leq U_{th} \text{ Sperrbereich } \cr \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) & \text{ für } 0 \leq U_{GS} - U_{th} \lt U_{DS} \text{ Sättigung } \cr \beta \left( 2 \left( U_{GS}-U_{th} \right) U_{DS} - U_{DS}^2 \right) & \text{ für } 0\leq U_{GS} - U_{th} \geq U_{DS} \text{ Triodenbereich } }$

$\beta = \frac{\mu_{n} \epsilon_{ox}}{2d_{ox}} \frac{W}{L} = \frac{1}{2} \mu_{n} C_{ox}^{'} \frac{W}{L} = \frac{1}{2} K_{n}^{'} \frac{W}{L} = \frac{1}{2} K_{n}$

$U_{th}= U_{th0} + \gamma \left( \sqrt{U_{SB}+2\phi_F}-\sqrt{2\phi_F}\right)$

$g_m = \frac{2 I_D}{U_{GS}-U_{th}}$

$g_d = \beta \left( U_{GS}-U_{th} \right)^2 \lambda = \frac{I_{DS}\lambda}{1+\lambda U_{DS}} \simeq I_{DS} \lambda$

$\omega_g = \frac{1}{RC}$

R=R_D=1/g_D, C=C_GD

Spannungsverstärkung:

Transitfrequenz: v_u=1

$v_u(0) = -R \cdot g_m = - \frac{g_m}{g_D} = - \frac{2}{ \left(U_{GS}-U_{th}\right) \lambda}$

$\omega_T =\frac{g_m}{C} \sim \frac{U_{GS}-U_{th}}{L^2}$

2020 09 07 Elektronik 3 11 MOSFET Prof. Dr. Joerg Vollrath

Elektronik 3

11 MOSFET

Prof. Dr. Jörg Vollrath

Video 11 MOSEFT

Rückblick und Heute

MOSFET als Schalter

MOSFET als Schalter

MOSFET Model Parameter

P-Channel Enhancement-Mode MOSFET Transistors

P-Channel Enhancement-Mode MOSFET Transistors 3N163

Messaufbau 3N163

Messung 3N163

MOSFET Parameterextraktion

Junction Field-Effect Transistor JFET (SFET Sperrschicht FET)

Leistungs MOSFET

Fragen: MOSFET

Gleichungen

Next