Elektronik 3

24 Rauschen

Prof. Dr. Jörg Vollrath

23 Anwendungen Operationsverstärker

Rückblick und Heute

Ringoszillator
Ladungspumpe
Spannungsregler
Gegenkopplung
Instabilität

Heute: Rauschen

Definition
Widerstandsrauschen
Diodenrauschen
Transistorrauschen
Rauschspannung
Rauschfaktor
SPICE Simulation

Reinhold: Kap. 7; S. 125-131
Jaeger: p. 1204,p. 823

Rauschen

Ein störendes Signal in einem Schaltkreis
Versuchsaufbau

Quelle, Schaltung, Messgerät (Oszilloskop, Spektrum Analysator)

Oszilloskop Messung

Zeit: x-Achse
Amplitude: y-Achse
Überlagerung von verschiedenen Frequenzen

Spektrum Analysator

Frequenz: x-Achse
Leistung (Amplitude):
y-Achse
Angabe: Rauschspannung $\frac{V}{\sqrt{Hz}}$

Eingangsbezogenes Rauschen

Messung am Ausgang
Wie überlagert sich das Rauschen dem Quellsignal?

Verstärkung A

Beispiel

An einem Verstärker mit einer Verstärkung von 100 wird ein weißes Rauschspektrum (konstant über der Frequenz) von Gleichspannung bis 100MHz von

$10 \frac{nV}{\sqrt{Hz}}$ gemessen.
Berechnen Sie die Eingangsrauschspannung.

$U_{onoise}^{2}(f)=(10 \frac{nV}{\sqrt{Hz}})^2 = 100 \cdot 10^{-18} \frac{V^2}{Hz}$

$U_{onoise,rms} = \sqrt{\int_{0}^{100MHz} 100 \cdot 10^{-18} df } V = 100 \mu V$

$U_{inoise,rms} = \frac{U_{onoise,rms}}{A} = 1 \mu V$
Wie groß ist die Spitze-Spitze-Spannung (peak-to-peak)?
Multipliziere den Effektivwert mit 6.

$U_{onoisepp} = 6 \cdot 100 \mu V = 0.6 mV$

Widerstandsrauschen

Statistische Stromschwankung durch thermische Bewegung der Ladungsträger.

Rauschstrom
Rauschspannung

Ersatzspannungsquelle
Ersatzstromquelle

Addition von Quellen:

$U_{r} = \sqrt{ \sum_{i=1}^{n} U_{ri}^{2}}$

$U_{rR}^2 (f) = 4 k T R$

$U_{rR,rms}^2 = \int U_{rR}^2 (f) df = 4 k T R \Delta f$

$U_{rR,rms} = \sqrt{4 k T R \Delta f}$

$I_{rR,rms} = \sqrt{\frac{4 k T \Delta f}{R}}$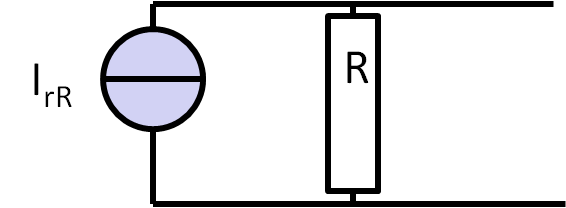

Beispiel: Δ f = 100 MHz
k = 13.8 · 10 ^-24 eV/K
T = 300 K

R [Ω]	1k	100k	1M
U_{r_{(f) [nV Hz^-0.5]}}	4.1	41	129
U_{rms_[mV]}	0.04	0.4	1.2
U_{pp_[mV]}	0.24	2.44	7.7

Beispiel ohmsche Widerstände

Berechnen Sie die effektive eingangs- und ausgangsbezogene Rauschspannung im Bereich bis 1kHz.

Ersatzschaltbild ausgangsbezogene Rauschspannung Parallelschaltung: Stromquellen

$I_{10k}^{2}(f) = \frac{4kT}{R_1} = \frac{4 \cdot 13.8 \cdot 10^{-24} \cdot 300 }{10000} \frac{A^2}{Hz} = 1.66 \cdot 10^{-24} \frac{A^2}{Hz}$

$I_{1k}^{2}(f) = 16.6 \cdot 10^{-24} \frac{A^2}{Hz}$

$I_{10k,rms}^{2} = \int_{0}^{1kHz} I_{10k}^{2}(f) df = 1.66 \cdot 10^{-21} A^2$

$I_{1k,rms}^{2} = 16.6 \cdot 10^{-21} A^2$

$U_{rout,rms} = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{10k,rms}^{2} + I_{1k,rms}^{2}} = 123 nV$

$U_{rin,rms} = 123 nV \frac{R_1 + R_2}{R_2} = 1.35 \mu V$
Alternative Superposition:

$U_{10k}(f) = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{10k}^{2}(f)} = 1.2 \frac{nV}{\sqrt{Hz}}$

$U_{1k}(f) = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{1k}^{2}(f)} = 3.7 \frac{nV}{\sqrt{Hz}}$

NoiseR.asc

Version 4
SHEET 1 880 680
WIRE 80 80 -32 80
WIRE 208 80 160 80
WIRE -32 96 -32 80
WIRE 208 128 208 80
WIRE -32 240 -32 176
WIRE 80 240 -32 240
WIRE 208 240 208 208
WIRE 208 240 80 240
WIRE 80 256 80 240
FLAG 80 256 0
FLAG 208 80 VA
SYMBOL voltage -32 80 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName VIN
SYMATTR Value ""
SYMBOL res 192 112 R0
SYMATTR InstName R2
SYMATTR Value 1k
SYMBOL res 176 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10k
TEXT -64 296 Left 2 !.noise v(VA,0) Vin dec 100 1 100000k
TEXT -56 32 Left 2 !.temp 300

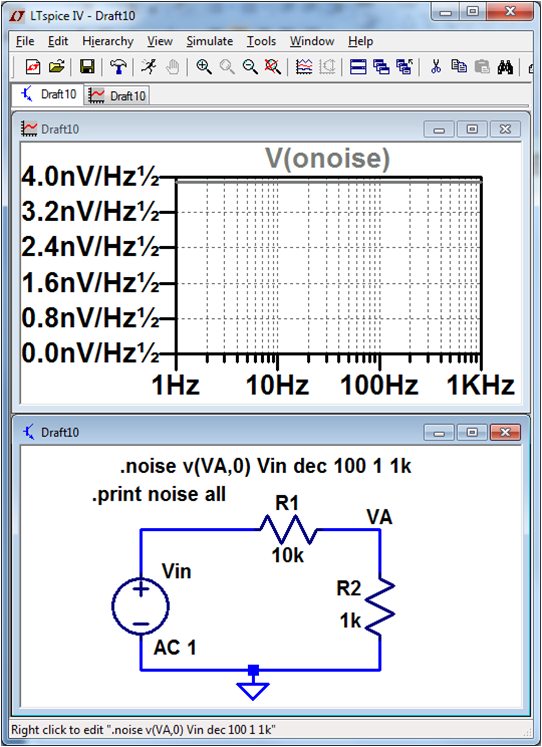
LTSPICE Verifikation

$U_{rout}(f) = 3.81 \frac{nV}{\sqrt{Hz}}$
'Strg' click auf die Beschriftung

$U_{rout, rms} = 122.7 nV$

Nachdenken über die Lösung

Je größer der Widerstand, desto größer die Rauschspannung
Einheiten
Quellenersatzschaltbild
Addition von Rauschspannungen und Strömen

Wurzel der Summe der Quadrate

Effektivwerte

Spannungsteiler um ein Signal auf den Eingangsbereich eines Verstärkers oder AD Wandlers an zu passen.

Beispiel RC Rauschen

Berechnen Sie die effektive ausgangsbezogene Rauschspannung.

$U_{out,noise}(f) = \sqrt{4 k T R } \frac{1}{1 + j \omega R C}$

$U_{out,noise,rms} = \sqrt{ \int_{0}^{f_{3db} \frac{\pi}{2}} U_{out,noise}^2 (f) df}$

$U_{out,noise,rms} = \sqrt{ f_{3db} \frac{\pi}{2} 4kTR}$

$U_{out,noise,rms} = \sqrt{ \frac{1}{2 \pi R C} \frac{\pi}{2} 4kTR} = \sqrt{ \frac{kT}{C} } = 64 \mu V$

NoiseRC.asc

Version 4
SHEET 1 880 680
WIRE 448 80 336 80
WIRE 576 80 528 80
WIRE 336 96 336 80
WIRE 576 144 576 80
WIRE 336 240 336 176
WIRE 448 240 336 240
WIRE 576 240 576 208
WIRE 576 240 448 240
WIRE 448 256 448 240
FLAG 448 256 0
FLAG 576 80 VA1
SYMBOL voltage 336 80 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName VIN
SYMATTR Value ""
SYMBOL res 544 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R4
SYMATTR Value 10k
SYMBOL cap 560 144 R0
SYMATTR InstName C1
SYMATTR Value 1pF
TEXT 272 296 Left 2 !.noise v(VA1,0) Vin dec 100 1 1000MEG
TEXT 360 328 Left 2 !.print noise all

Diodenrauschen

Schrotrauschen (Shot noise)

Ladungsträger überschreiten Grenzflächen (Potenzialbarrieren)
$I_{rDS}(f)=\sqrt{2 q I}$
I Diodenstrom, Arbeitspunktstrom, q Elementarladung

Funkelrauschen (Flicker noise,1/f)
$I_{rDF}(f) = \sqrt{\frac{K_F I^{AF}}{f^{b}}}$

KF, AF und b Materialparameter
Silizium KF=10-16, AF=1, b=1

Thermisches Rauschen $I_{rDR}(f)$

Bahnwiderstände der Diode

Summe
$I_{rD}(f) = \sqrt{2 q I + \frac{K_F I^{AF}}{f^{b}} + I_{rDR}^{2} (f) }$

DiodeR.asc

Version 4
SHEET 1 1492 680
WIRE 96 96 -32 96
WIRE 240 96 176 96
WIRE -32 144 -32 96
WIRE 240 144 240 96
WIRE -32 256 -32 224
WIRE 96 256 -32 256
WIRE 240 256 240 208
WIRE 240 256 96 256
WIRE 96 272 96 256
FLAG 96 272 0
FLAG 240 96 VA
SYMBOL voltage -32 128 R0
WINDOW 3 15 131 Left 0
WINDOW 123 15 103 Left 0
WINDOW 39 0 0 Left 0
SYMATTR InstName Vin
SYMATTR Value 5
SYMATTR Value2 AC 1
SYMBOL res 192 80 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL diode 224 144 R0
SYMATTR InstName D1
SYMATTR Value 1N914x
TEXT -96 -40 Left 0 !.noise v(VA,0) Vin dec 100 1 100MEG
TEXT -96 -8 Left 0 !.model 1N914x D(Is=2.52n Rs=.568 N=1.752 Cjo=4p \n+ KF=1E-16 AF=1 M=.4 tt=20n Iave=200m Vpk=75 \n+ mfg=Motorola type=silicon)

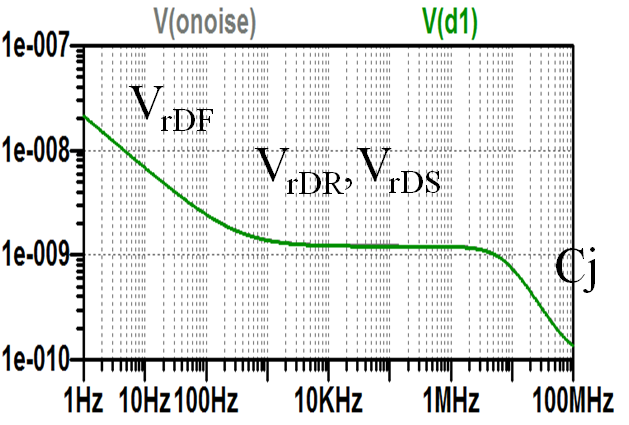
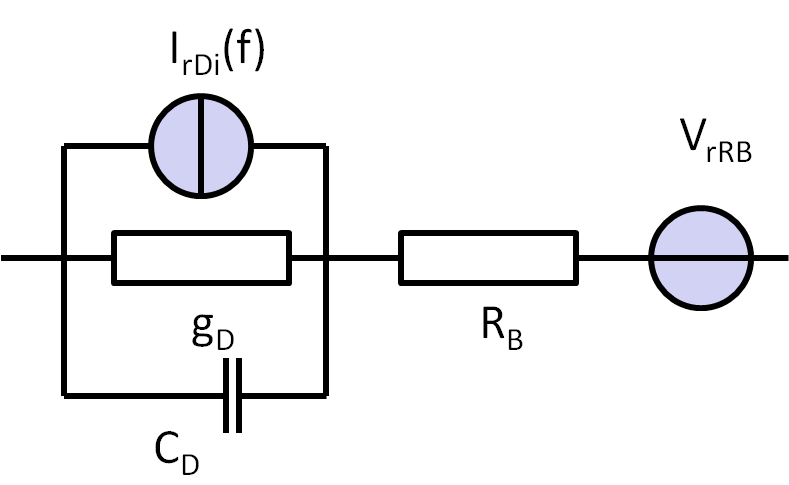
Diodenrauschersatzschaltung

Zwei Quellen:

Strom
$I_{rDi} = \sqrt{2 1 I \Delta f + \frac{K_F I^{AF} \Delta f}{}f^{b}}$
Spannungsquelle für den Bahnwiderstand
$V_{rRB} = \sqrt{4kTR \Delta f}$

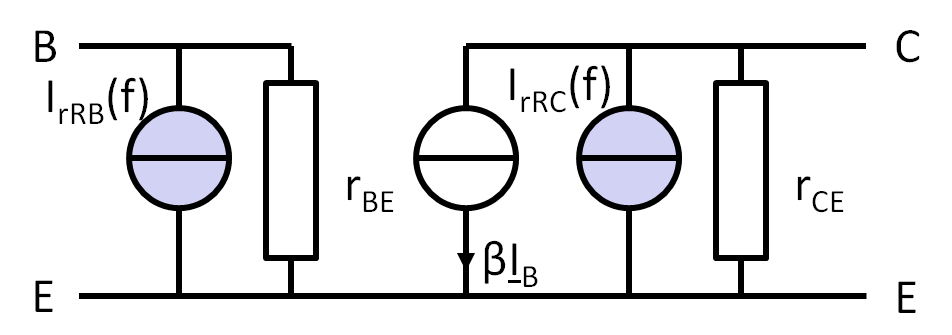
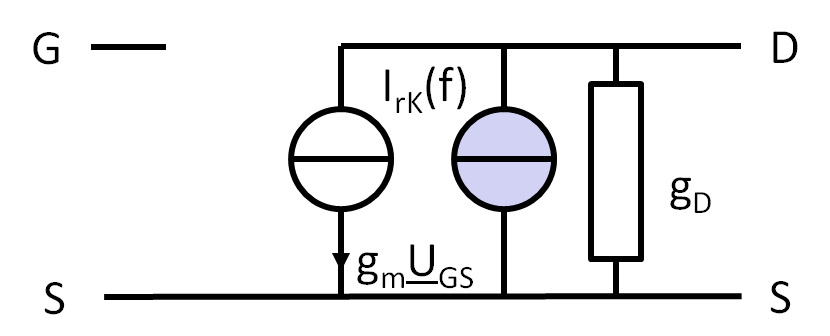
Transistorrauschen

Bipolartransistor: Diode BE, BC
Feldeffekttransistor
- Kanalrauschen I_rK
- 1/f Rauschen IrKF
- Thermisches Kanalrauschen IrKt
- Schrotrauschen Drain-Bulk, Source Bulk

$I_{rK}(f) = \sqrt{I_{rKt}^{2}(f) + I_{rKF}^{2}(f)}$

$I_{rKF}(f) = \sqrt{\frac{K_F I_D^{AF}}{C_{ox} f^b}}$

$I_{rKt}(f) = \sqrt{\frac{8}{3} k T g_m }$

Rauschfaktor

Signal Rausch Abstand

Signal to noise ratio (SNR)
Quotient aus Signalleistung P_s und Rauschleistung P_r

Rauschfaktor, Rauschzahl:
- Verhältnis der Signalrauschabstände von Eingang und Ausgang
Rauschmaß: logarithmierter Rauschfaktor

$SNR = \frac{P_S}{P_r}$

$SNR_{dB} = 10 \cdot log \left( \frac{P_S}{P_r} \right) = 10 \cdot log \left(P_S\right) - 10 \cdot log \left(P_r\right)$

$F = \frac{SNR_E}{SNR_A}$

$F_{dB} = 10 \cdot log \left( F \right)$

Zusammenfassung Rauschen

Spannung oder Strom
Frequenzabhängige Größen: $V/\sqrt{Hz}, A/\sqrt{Hz}$
Effektivwert: $V_{r,RMS} = \sqrt{\int V_{rR}^2(f)df}$
Amplitude größer als Effektivwert
Mehrere Quellen: Wurzel aus der Summe der Quadrate
Umrechnung der Quellen
Widerstand, Diode, Transistor

Thermisches Rauschen: 4kTR
1/f Rauschen, Funkelrauschen: $\frac{K_F I^{AF}}{f^{b}}$
Schrotrauschen: 2qI

Kapazität: Tiefpass, begrenzt Rauschen
Signalrauschverhältnis
Rauschzahl

2020 09 07 Elektronik 3 24 Rauschen Prof. Dr. Joerg Vollrath