Übersicht
|
|
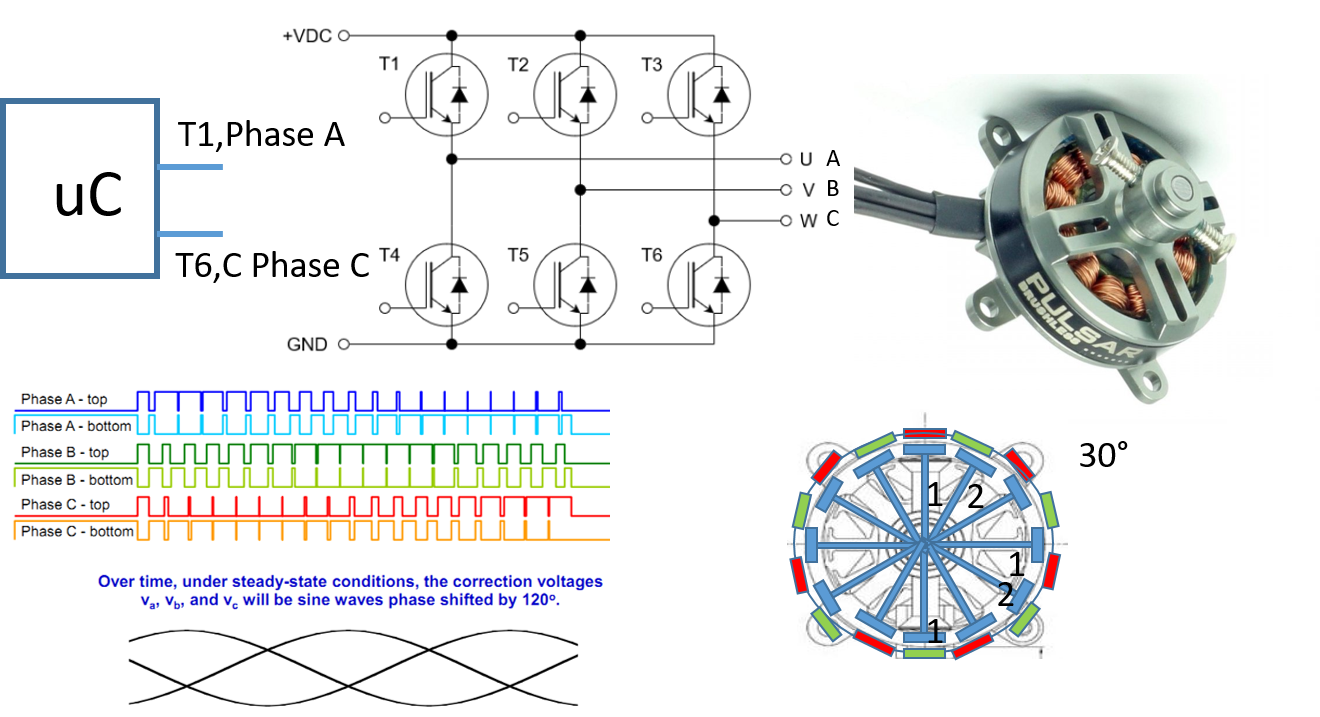
Das Bild zeigt einen Mikroprozessor (uC) der die Leistungstransistoren für die 3 Phasen des Motors ansteuert.
Die Pulsweitenmodulation für die Ansteuerung der Leistungstransistoren zur Sinussignalerzeugung ist abgebildet.
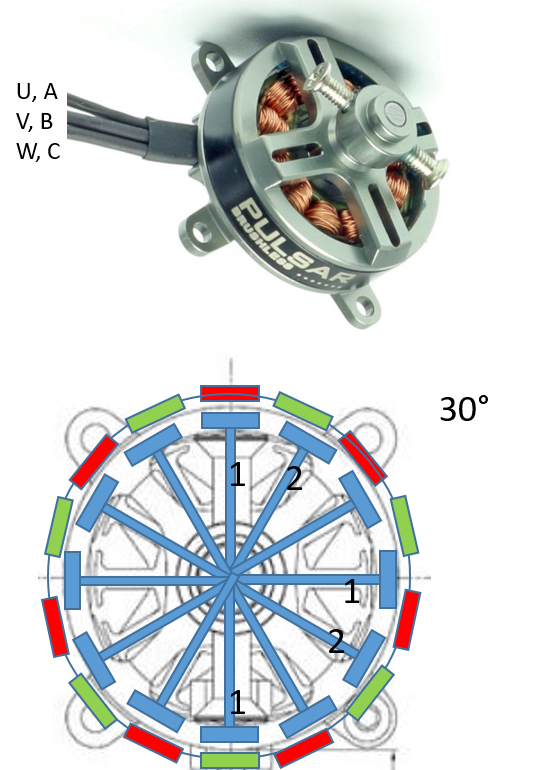
Wie schematisch gezeigt besteht der Motor aus 14 Magneten im Läufer aussen und 12 Wicklungen, zu 3 Phasen verbunden, im Anker.
Mit einem geeigneten LTSPICE Motormodell kann man die Ansteuerung optimieren. Dabei wird eine geeignete Betriebsspannung, Treibertransistoren und eine geregelte Ansteuerung implementiert. Der Motor soll mit möglichst geringer Energie kontinuierlich bei verschiedenen Drehzahlen und Lastwechseln arbeiten.
Motoren
3 PhasenPermanent Magnet Synchronous Motor (PMSM)
|
|
Der Strom in den Phasen A, B, C erzeugt ein magnetisches Feld, das mit den
Permanentmagneten interagiert und zu einem Drehmoment führen kann.
Motorgleichungen

Man sieht ein einphasiges Modell für einen Motor mit elektrischen und
mechanischen Größen. Das Drehmoment und eine Last fehlt hier.
Im Internet findet man Modelle mit einer Phase, für asynchron Motoren ohne Permanentmagnet, ohne Back EMF und transformiert von einem 3-phasigen auf ein 2-phasiges System.
Für eine bestimmte Anwendung muss man ein vorhandenes Modell anpassen.
Im Internet findet man Modelle mit einer Phase, für asynchron Motoren ohne Permanentmagnet, ohne Back EMF und transformiert von einem 3-phasigen auf ein 2-phasiges System.
Für eine bestimmte Anwendung muss man ein vorhandenes Modell anpassen.
Motorgleichungen
|
Strom I und Drehmoment (Torque) \( T = K_f \cdot pp \cdot \left( I_a \cdot cos(\phi) + I_b \cdot cos(\phi + \frac{2 \pi}{3}) + I_c \cdot cos(\phi - \frac{2 \pi}{3}) \right) \) Drehmoment T und Winkelgeschwindigkeit ω (omega, w): \( \omega = J_{inertia} \cdot \int (T - T_{load} - B_{friction} \cdot \omega ) dt \) Winkelgeschwindigkeit ω und Winkel φ (phi): \( \phi = \int \omega dt \) Gegeninduktionsspannungen (Back electromagnetic force): \( V_{ea} = K_f \cdot pp \cdot \omega \cdot cos(\phi) \) \( V_{eb} = K_f \cdot pp \cdot \omega \cdot cos(\phi + \frac{2 \pi}{3}) \) \( V_{ec} = K_f \cdot pp \cdot \omega \cdot cos(\phi - \frac{2 \pi}{3}) \) pp: Polpaare Kf: Back EMF Konstante B: Reibung viscious friction |
Der Strom in den Phasen A, B, C erzeugt ein magnetisches Feld, das mit den
Permanentmagneten interagiert und zu einem Drehmoment führen kann.
Eine Integration wird durch die Kapazitäten durchgeführt.
Die Kapazität Cj modelliert die Trägheit J (Inertia).
Der Widerstand RB modelliert die Reibung (Friction)
Eine zusätzliche Stromquelle B_Load1 kann verschiedene Reibungsarten simulieren.
Die Kapazität C1 berücksichtigt zur Bestimmung von φ die Polpaarzahl.
Für einen Motor muss man folgende Parameter bestimmen:
[] Matlab PMSM parameter identification
[] Electrical equivalent circuit for modelling permanent magnet synchronous motors, Esra Kandemir Beser, 2021
[] Induction 3-phase motor model, Kubov, Sohor, 2013
[] AB-025 Using SPICE To Model DC Motors, precision micro drives
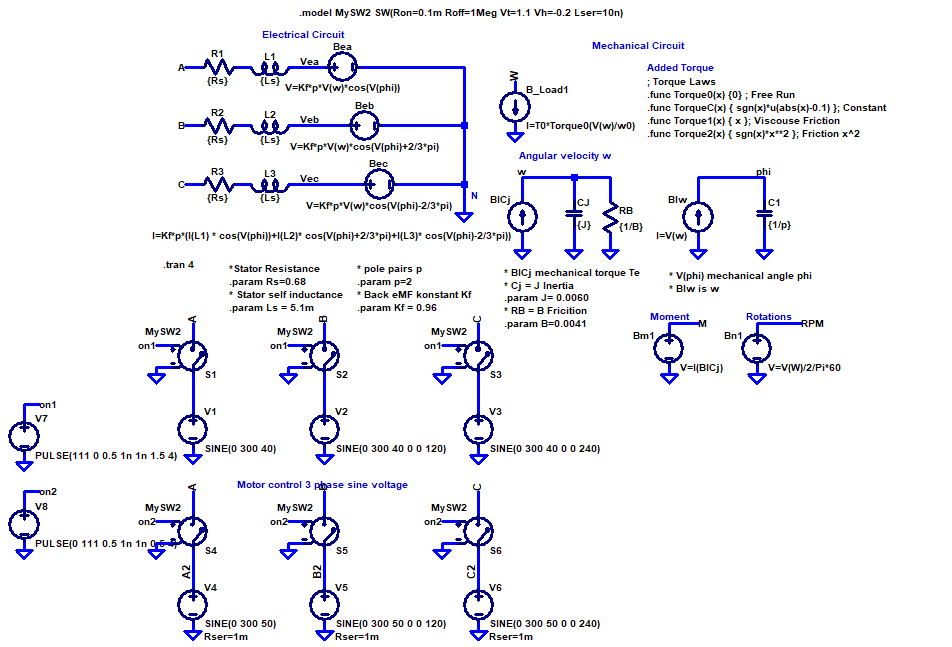
MotorAC_Test.asc
Während einer transienten Simulation über 4s schaut man sich die Ströme I(R1), I(R2),I(R3) an.
Zuerst wird der Motor mit 40 Hz Sinussignal betrieben und dann die Versorgung nach 0.5 s getrennt und der Motor läuft aus (Spanningsquelle V7, on1).
Nach 3 s wird der Motor dann mit 50 Hz Sinussignal betrieben (Spanningsquelle V8, on2).
Eine Integration wird durch die Kapazitäten durchgeführt.
Die Kapazität Cj modelliert die Trägheit J (Inertia).
Der Widerstand RB modelliert die Reibung (Friction)
Eine zusätzliche Stromquelle B_Load1 kann verschiedene Reibungsarten simulieren.
Die Kapazität C1 berücksichtigt zur Bestimmung von φ die Polpaarzahl.
Für einen Motor muss man folgende Parameter bestimmen:
- Poolpaarzahl, maximale Drehzahl, maximale Betriebsspannung, maximaler Strom
- Elektrisch: Rs, Ls
- Elektrisch: Kf
- Reibung und Trägheit
[] Matlab PMSM parameter identification
[] Electrical equivalent circuit for modelling permanent magnet synchronous motors, Esra Kandemir Beser, 2021
[] Induction 3-phase motor model, Kubov, Sohor, 2013
[] AB-025 Using SPICE To Model DC Motors, precision micro drives
Motor with test circuit

MotorAC_Test.asc
Während einer transienten Simulation über 4s schaut man sich die Ströme I(R1), I(R2),I(R3) an.
Zuerst wird der Motor mit 40 Hz Sinussignal betrieben und dann die Versorgung nach 0.5 s getrennt und der Motor läuft aus (Spanningsquelle V7, on1).
Nach 3 s wird der Motor dann mit 50 Hz Sinussignal betrieben (Spanningsquelle V8, on2).
Aufgabe Motorgleichungen
Spannungsversorgung
Es sei ein Motor mit Rs = 0.75 Ω, Ls = 0.05 mH, Kemf = 0.68 Vrms/kRPM, einer Reibung 82.8 nNms und einer Trägheit von 230 nNms2 gegeben.
Wie groß muss die angelegte Spannung sein, damit bei einer Last TL = 0 eine Drehzahl RPM = 10000 rpm/min erreicht werden kann?
Motorvergleich
Es sei ein Motor1 mit Rs1 = 0.75 Ω, Ls1 = 0.05 mH, Kemf1 = 0.68 Vrms/kRPM, einer Reibung1 82.8 nNms und einer Trägheit1 von 230 nNms2 gegeben.
Es sei ein Motor2 mit Rs2 = 3 Ω, Ls2 = 0.2 mH, Kemf2 = 0.5 Vrms/kRPM, einer Reibung2 82.8 nNms und einer Trägheit2 von 230 nNms2 gegeben.
Welcher Motor ist für eine Anwendung von RPM = 5000 und einer Last von TL = 10 Nm besser geeignet?
Motorgleichungen im LTSPICE Model
Die Spannungsquellen V1, V2, V3 erzeugen die Motorsteuerungsspannungen A, B, C.
Jede Motorphase hat ein R{Rs}, L und eine gesteuerten Spannungsquelle (Back EMF).
V = KI · p · ω · cos(φi+(0,120,240°))
p: Polpaar
Rs: Stator Resistance
Ls: Stator inductance
Die Kreisfrequenz ω (angular velocity) wird durch die gesteuerte Stromquelle BICj, Cj, RB und B_Load1 modelliert.
Cj modelliert die Trägheit
RB modelliert die Reibung
B_Load modelliert die Last (.func Torque..)
\( I_{BICj} = K_f \cdot p \cdot \sum_1^3{I_{i} \cdot cos( \phi + \phi_i)} \)
Aus der Kreisfrequenz V(w) wird der Winkel φ mit der Stromquelle BIw und der Kapazität C1 berechnet
Weiterhin wird das Drehmoment M und die Drehzahl RPM modelliert.
Jede Motorphase hat ein R{Rs}, L und eine gesteuerten Spannungsquelle (Back EMF).
V = KI · p · ω · cos(φi+(0,120,240°))
p: Polpaar
Rs: Stator Resistance
Ls: Stator inductance
Die Kreisfrequenz ω (angular velocity) wird durch die gesteuerte Stromquelle BICj, Cj, RB und B_Load1 modelliert.
Cj modelliert die Trägheit
RB modelliert die Reibung
B_Load modelliert die Last (.func Torque..)
\( I_{BICj} = K_f \cdot p \cdot \sum_1^3{I_{i} \cdot cos( \phi + \phi_i)} \)
Aus der Kreisfrequenz V(w) wird der Winkel φ mit der Stromquelle BIw und der Kapazität C1 berechnet
Weiterhin wird das Drehmoment M und die Drehzahl RPM modelliert.
Motor Ansteuerung
|
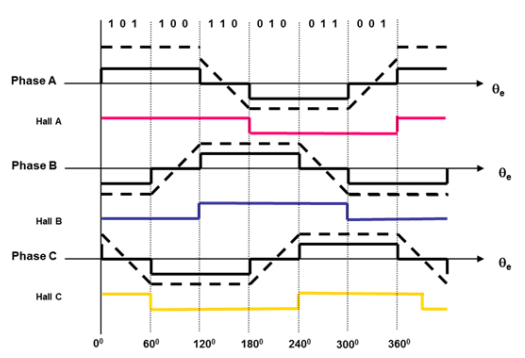
Block Commutation |
|
|
Sine Commutation |
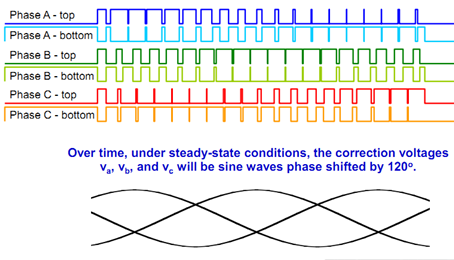
|
Motor Ansteuerung in LTSPICE
|
Die Signale einer PWM Sine Commutation |
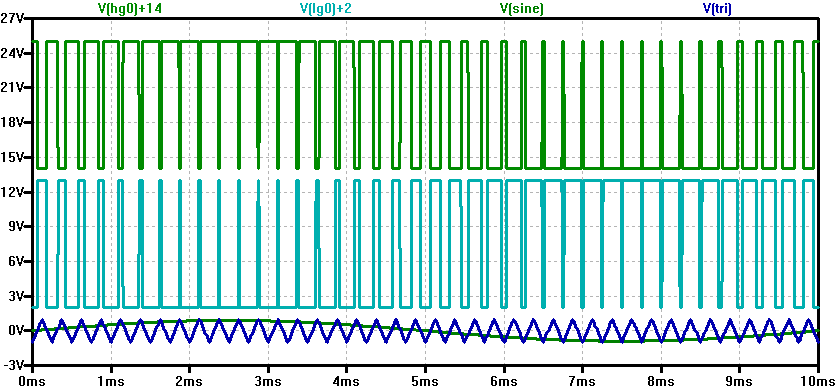
|
|
Schaltkreis mit Spannungsquellen |
SinePWM.asc
Parameter:
m = 0..1 Modulation of PWM
fm: Sine frequency
fc: PWM frequency
Vmax: maximum voltage
Outputs:
High side driver: HG1, HG2, HG3
Low side driver: LG1, LG2, LG3
Motor Ansteuerung (Sine Commutation) mit dem Electronic Explorer
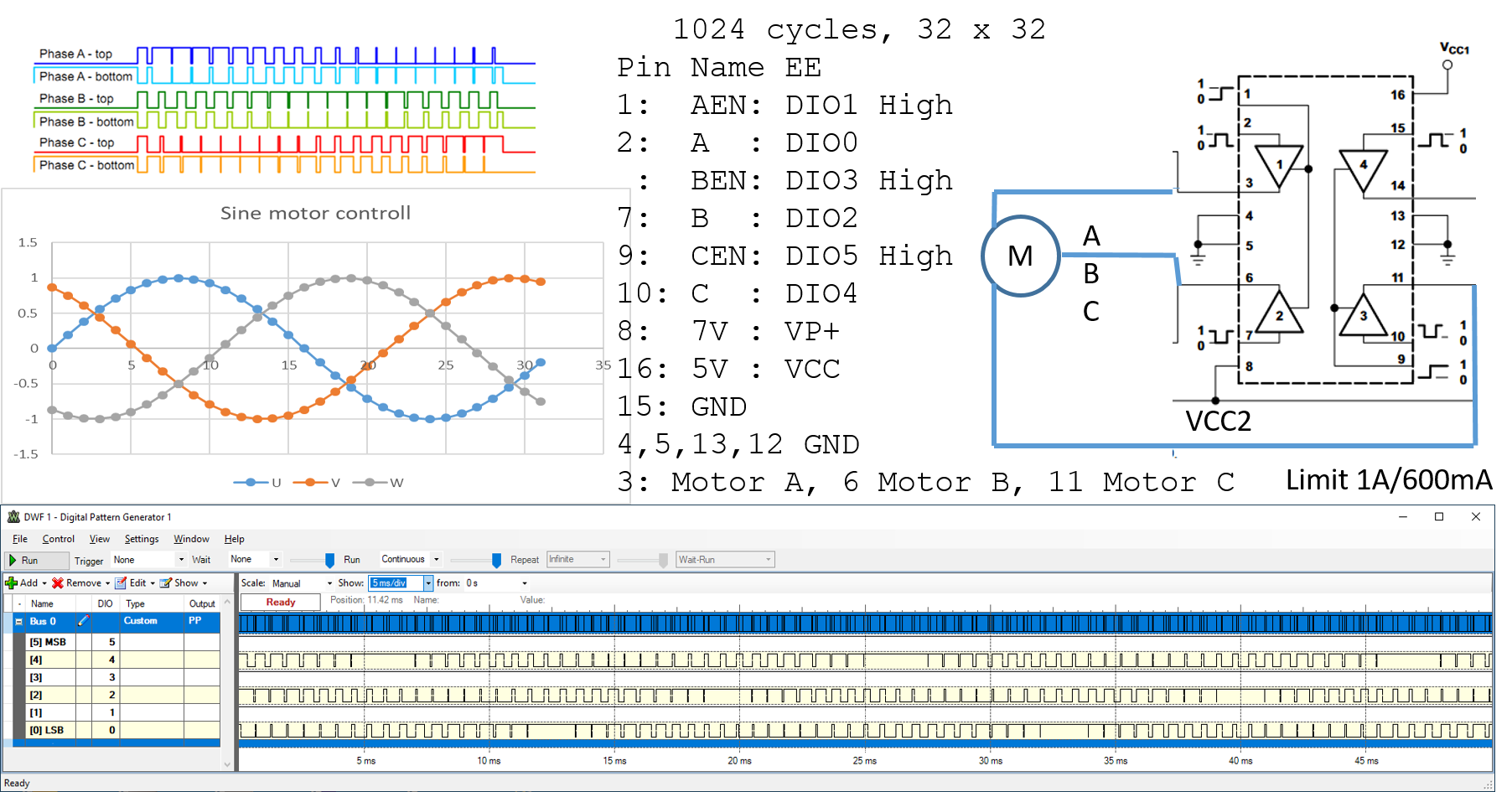
Die Signale einer Sine Commutation
Schaltkreis mit Motor und L293D
Digital Output files with control signals:
Sine CommutationmotorS1.csv
Sine Commutation motorS2.csv
Patterns out
Add, Bus
Make available DI0..DIO5 to selected.
Type: Custom
Output: PP
Edit, Parameters
Import File
Open file
Browse
Motor Ansteuerung (Block Commutation) mit dem Electronic Explorer
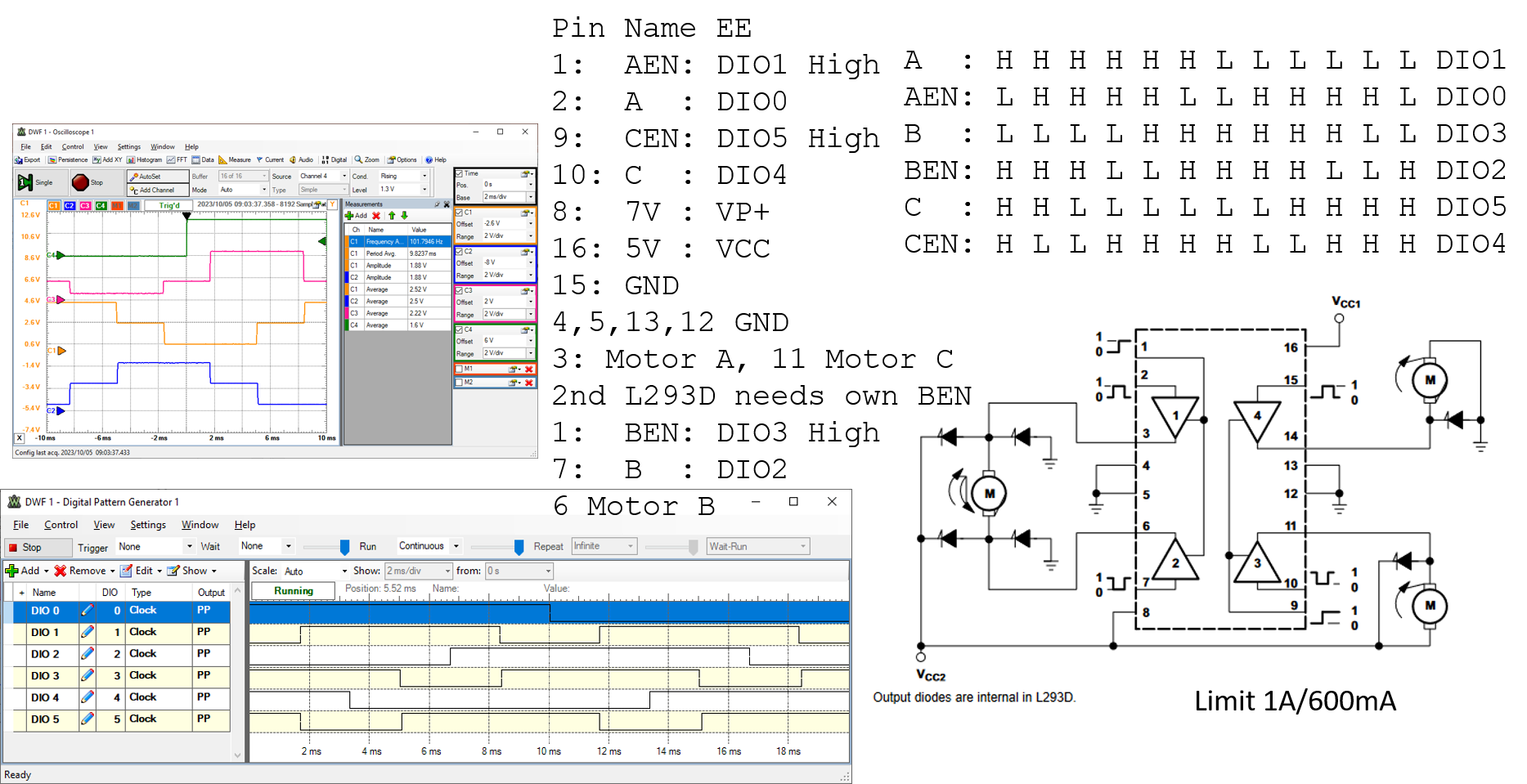
Die Signale einer Block Commutation
Schaltkreis mit Motor und 2 Bausteinen L293D, da man 3 enable Signale benötigt.
Die Signalfrequenz ist niedriger als bei der Sine Commutation.
Digital Output files with control signals:
Block Commutationmotor.csv
Patterns out
Add, Bus
Make available DI0..DIO5 to selected.
Type: Custom
Output: PP
Edit, Parameters
Import File
Open file
Browse
Frequency: 1 kHz
VP+: 6 V (834mA), VCC 5V (50 mA)
Fragen
Messung, Simulation, Schaltungsentwurf
- Wie werden die Parameter (Rs, Ls, Kf, Torque, B, p, J) bestimmt (Simulation, Messung)?
- Welche Spannung, welcher Strom werden für eine gewünschte Drehzahl und ein gewünschtes Drehmoment benötigt?
- Wie fährt man den Motor optimal an bzw. bremst den Motor?
- Wie reagiert der Motor auf Drehzahl und Laständerungen?
- Ändert sich die messbare Induktivität mit dem Winkel, der Position?
- Kann man die Motorposition durch ein elektrisches Prüfsignal bestimmen?
- Welches sind die optimale Frequenz, Spannung und die MOSFETs für die H-Brücke?
Motor Parameterbestimmung:
|
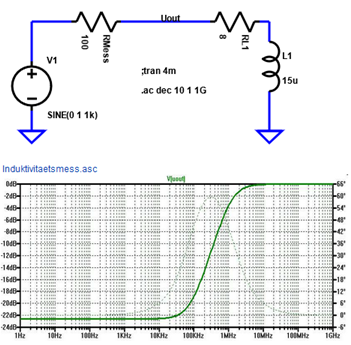 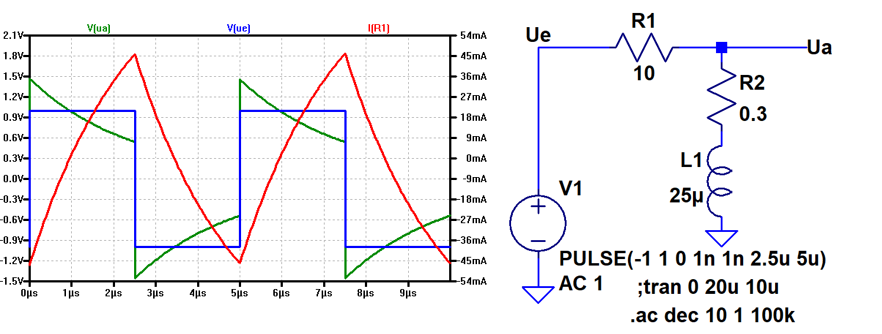 |
Motor Parameterbestimmung Kf, J,
|
 |
In der Simulation wird von 0 s bis 0.5 s eine Frequenz von 40 Hz angelegt (rotes Signal V(on1) für den Schalter), um dann auf 50 Hz zu wechseln V(on2). Ab 1 s sind beide Schalter offen, die abnéhmende Back EMF Spannung ist sichtbar und der Motor wird langsamer, V(w) wird kleiner.
MotorAC_Test.asc
Motor Basic Measurements with Electronic Explorer
|
 |
Motor control evaluation board
|

|
P-NUCLEO-IHM001 STM Motor evaluation kit 80.- Euro 2023
Infineon: iMOTION 2.0 platform
iMOTION controller, power stage (IPM), MCE Wizard and MCE designer
Texas Instruments: TIDM-RM46XDRV8301KIT Three-Phase BLDC / PMSM Motor Drive with High-Performance Microcontrollers Reference Design
Motor profiler
|
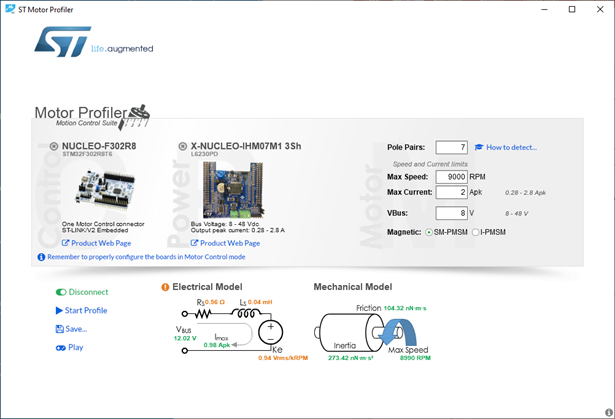
|
Zusammenfassung
- Motoren: DC, 3 Phasen Permanent Magnet Synchronous Motor (PMSM)
- Motorensystem
Elektronische Steuerung: Block commutation, sine H-bridge PWL signal
Systemparameter: Polpaarzahl, Rs, Ls, KEMF, Trägheit (Inertia), Reibung (Friction)
Interessante Größen: Eingangsspannung und -strom, Winkelgeschwindigkeit, Drehzahl, Position, Drehmoment
Erweiterungen: Turn-on voltage, stall, variable inductance - Theorie und Gleichungen
- Simulation mit LTSPICE
Abbildung eines 3 Phasen Systems und mechanischer Größen in ein elektrisches Schaltbild - Messung an einem 3 Phasen Permanent Magnet Synchronous Motor (PMSM)
Electronic Explorer
Evaluation Board (STMicroelectronics)
Todo
To Do:
- LTSPICE: Sine and block commutation circuit and simulation
- LTSPICE: Extract motor parameters from simulation
- LTSPICE: Verify real motor measurement, simulation and theory
- LTSPICE: FOC control and other control schemes (Open source Arduino library, Github)
- LTSPICE: Optimize, DC level, transistors, circuit for a motor application
- Details Electronic Explorer measurements
Digital waveforms, R, L, BackEMF measurement
Different drivers
Measure waveforms on STMicro Evaluation board - Measurement of magnetic field B of motor windings and magnets
- Measurement of absolute position with high frequency sine signal added to control signals
- Implement current measurement on EE Board
- Implement hardware sine (analog voltage in) to PWM
- Use and present drone motor control XXD HW30A 30A ESC
- Limits of a motor simulation: rpm, voltage, torque
Literatur
[1] Texas Instruments Motor Control Compendium 2010[2] Matlab PMSM parameter identification
[3] Electrical equivalent circuit for modelling permanent magnet synchronous motors, Esra Kandemir Beser, 2021
[4] Comparative Modelling and Experimental Verification of a PMSM Drive System, Gullu Boztas, 2022
[5] Induction 3-phase motor model, Kubov, Sohor, 2013
[6] AB-025 Using SPICE To Model DC Motors, precision micro drives
[7] MOTORCONTROLKIT_12V, Infineon
[8] P-NUCLEO-IHM001 STM Motor evaluation kit
[9] STM motor profiler tool
[10] Brushless Motor PULSAR Shocky Pro 2204 | 1800 KV
[11] Drone motor control, XXD HW30A 30A ESC Schematic, Nickson Yap
[12] 3 Phase AC Motor ltWiki ltspice goodies
[13] Github: SimpleFOClibrary
Grundlagen
Beser:
\( T_e - T_L = J \frac{d \omega_m}{dt} + B \cdot \omega_m \)
Te: electromagnetic torque
TL: load torque
J: inertia torque
B: viscious friction coefficient
Magnete: lm = 40 mm, bm = 10mm, hm = 5 mm; B = 170 mT
Kupferwicklung
Draht: DDraht = 0.45 mm inklusive 0.05 mmm Lackdicke
ADraht = 0.159 mm2
Maximale Stromdichte Kupfer: Jmax = 3.58 A mm-2
IDraht,max = ADraht · Jmax = 0.45 A
Spezifischer Widerstand Kupfer bei 20 °C:
ρKupfer = 17.8 nΩm
RDrahtx = 0.14 Ω m-1
Magnetfeld einer Spule:
\( B = \frac{\mu_0 \cdot N \cdot I}{l} \)
Permeabilität µ0 = 1.26E-6 NA-2
l: Länge der Spule
N: Anzahl Windungen
I: Strom
\( L = \frac{\mu_0 \cdot N^2 \cdot A}{l} \)
A: Querschnitt
N: Windungszahl
l: Länge der Spule
Motor development Kits
Texas Instruments
DRV8301-69M-KIT 350.-
DRV8711EVM Stepper Motor 110.-
Infineon
EVAL-IMM101T 70.-
Renesas
RTK0EM0006S01212BJ (RX23T) 360.-
Vergleich Spule und Magnet
|
Mit einem Draht mit einem Durchmesser D=0.45 mm wird ein
Volumen mit einer Grundfläche (Spulenfläche) von
L = 40 mm und B= 10 mm und einer Höhe H=5 mm gefüllt. Bei einem Dauermagneten gleichen Volumens wird ein B = 150 mT gemessen. Wie gross ist das Magnetfeld der Spule? LDraht = 9.68 m NSpule = 121 B = 12.6 mT RSpule = 1.37 Ω Imax = 0.45 A USpule = 0.6 V L = 1.47 mH |

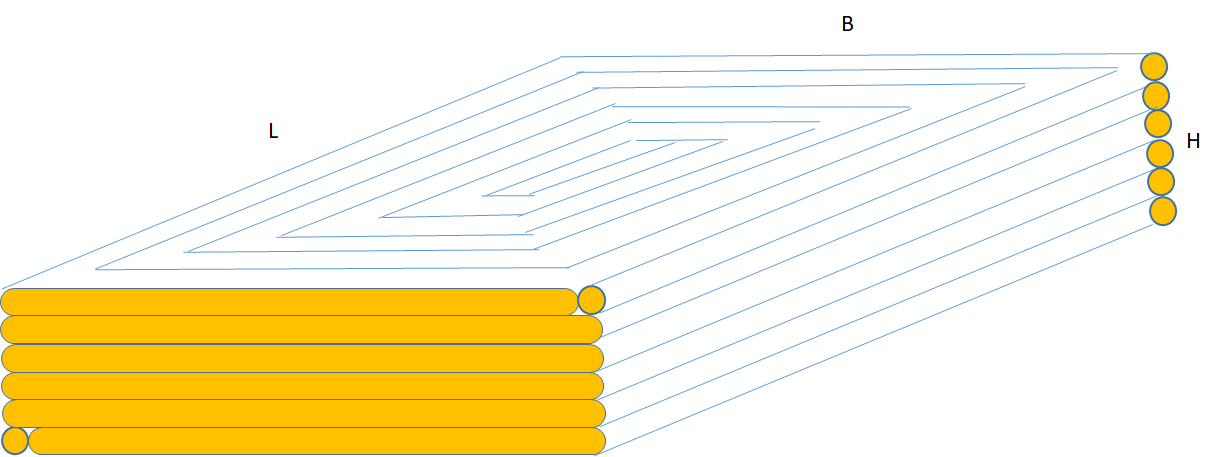
\( B = \frac{\mu_0 \cdot N \cdot I}{l_{Spule}} \) \( L = \frac{\mu_0 \cdot N^2 \cdot A}{l_{Spule}} \) \( R_{Wicklung} = \rho_{Cu} \cdot \frac{l_{Draht}}{A_{Cu}} \) |
Anzahl der Drahtlagen: DL = H/D = 11
Schneckenwindungen füllen die Grundfläche: SW = B/D = 22
Die Windungszahl der Spule ergibt sich dann zu:
N = DL * SW/2 = 121
Die Länge der Spule ist: LSpule = DL * SW * L = 11 * 22 * 40 mm = 9680 mm = 9.68 m
u0 = 1.26E-6 NA-2
Der maximale Strom für diesen Draht ist wie oben berechnet Imax = 0.45 A
Es ergibt sich ein B von:
B = u0 N I / LSpule = 1.26E-6 * 121 * 0.45 / 0.005 T = 1.26E-6 * 10000 T = 12.6 mT
Das Magnetfeld der Spule ist 15 mal kleiner als das Magnetfeld des Dauermagneten.
Kupferwiderstand der Wicklung:
\( R_{Wicklung} = \rho_{Cu} \cdot \frac{l_{Draht}}{A_{Cu}} \)
\( R_{Wicklung} = 0.0178 \frac{\Omega mm^2}{m} \cdot \frac{9.68 m}{0.126 mm^2} = 1.37 \Omega \)
Betriebsspannung der Spule:
\( U = I \cdot R = 0.45 A 1.37 \Omega = 0.62 V \)
Induktivität einer Zylinderspule:
\( L = \frac{\Phi}{I} = \frac{\mu_0 \cdot N^2 \cdot A}{l} = \frac{1.26 \cdot 10^{-6} NA^{-2} \cdot (121)^2 \cdot 0.04 m \cdot 0.01 m}{ 0.005 m} = 1.47 mH\)
Ein dickerer Draht führt zu weniger Windungen mit größerem Querschnitt in einem konstanten Volumen.
Das B Feld bleibt konstant B ∝ N · I
Die Induktivität nimmt mit einem dünnerem Draht und mehr Windungen zu.
L ∝ N2
Der Widerstand nimmt ab und die maximale Gesamtleistung P = U · I bleibt gleich.
Doppelter Drahtquerschnitt, halbe Drahtlänge: R ∝ l/A
Bei kleinerer Spannung wird der maximal zulässige Strom erreicht.
Vermutung: Da eine große Induktivität kein Schaltungstechnisches Problem ist sollte man dünne Drähte verwenden, um eine hohe Versorgungsspannung zu verwenden.
Bei dünnen Drähten ist das Volumenverhältnis Draht zu isolation etwas schlechter.
Es könnte eine Durchschlagsspannung zwischen 2 Windungen erreicht werden (Wicklungsanordnung, länge).
