Elektronik 308a RauschenWiderstandsmessungProf. Dr. Jörg Vollrath08 Rauschen |
"Elektronik/2024_08a_Elektronik3_WiderstandsRauschenMessung.html"
Dieses Dokument zeigt die praktische, preiswerte Umsetzung einer Widerstandsrauschmessung.
Es wird die Theorie des weissen Widerstandsrauschens erläutert, eine Simulation durchgeführt und eine Breadboardschaltung mit einer Batteriespannungsversorgung aufgebaut.
Der Effektivwert des Rauschens kann mit einem True RMS Multimeter oder einem Oszilloskop gemessen werden.
Zur Bestimmung der Verstärkung und Bandbreite der Schaltung muss die Übertragungsfunktion mit einem Signalgenerator und einem Oszilloskop bestimmt werden (Electronic Explorer, ADALM2000, Analog Discovery 2).
Dieses Dokument zeigt die praktische, preiswerte Umsetzung einer Widerstandsrauschmessung.
Es wird die Theorie des weissen Widerstandsrauschens erläutert, eine Simulation durchgeführt und eine Breadboardschaltung mit einer Batteriespannungsversorgung aufgebaut.
Der Effektivwert des Rauschens kann mit einem True RMS Multimeter oder einem Oszilloskop gemessen werden.
Zur Bestimmung der Verstärkung und Bandbreite der Schaltung muss die Übertragungsfunktion mit einem Signalgenerator und einem Oszilloskop bestimmt werden (Electronic Explorer, ADALM2000, Analog Discovery 2).
Überblick
- Herausforderungen einer Widerstandsrauschmessung
- Widerstandsrauschen
- LTSPICE Simulation
- Schaltungsrealisation
- Ergebnisse
- Zusammenfassung
Widerstandsrauschen
 | |
|
Mit einer Verstärkung von vu = 4416 und einer Bandbreite von fbw = 20 kHz konnten bei Widerständen von 10 kΩ..100 kΩ Effektivwerte zwischen 16..30 mV gemessen werden. |
 |
Die Bilder zeigen einen Überblick der Arbeit mit Simulationsschaltplan, Breadboardaufbau,
gemessener Übertragungsfunktion und Zusammenfassung der Messergebnisse.
Der Schaltplan links oben für die Simulation verwendet AWG1 als Spannungsquelle für die Übertragungsfunktion.
Bei einer Rauschsimulation wird dieser Schaltungsteil abgetrennt und nur ein Widerstand mit dem Eingang des Operationsverstärkers Vin verbunden.
Beim praktischen Breadboard Aufbau rechts oben wurden 4 AA Batterien mit VP+ = 3 V und VP- = -3 V zur Spannungsversorgung (schwarzer Kasten rechts) eingesetzt.
Der minimale Rauscheffektivwert der Messung bei kleineren Widerstandswerten lag bei 14 mV.
Die Steigung der Ausgleichsgeraden von 0.0072 mV2 pro Ω
entspricht vu2 = 4 k T fbw R = 0.0069 mV2 R pro Ω in etwa dem erwarteten Wert.
Zur Messung der Verstärkung und des Frequenzganges wurde ein externes Sinus- und Rauschsignal mit einem Spannungsteiler (20 kΩ, 100 Ω) von 50 mV Amplitude auf 250 µV (Faktor 200) heruntergeteilt.
Mit einer Aluminiumabschirmung konnte für 200kΩ ein Schwingen des Ausgangssignals bei grossen Widerstandswerten vermieden werden.
Bei der Verwendung eines doppelten Spannungsteilers von 10kOhm und 100 Ohm, hatte die Übertragungsfunktion zwischen 1 kHz und 10 kHz eine zu kleine Verstärkung (Kapazitäten, Leckstrom).
Größere Verstärkung (10 statt 2) beim Filter führten auch zum Schwingen.
Es fehlen noch Bufferkapazitäten bei der Spannungsversorgung.
Das Oszilloskop des Electronic Explorers wurde mit einer Empfindlichkeit von 100mV/div und einer Zeitbasis von 1ms/div verwendet und der AC RMS Wert abgelesen.
Der Schaltplan links oben für die Simulation verwendet AWG1 als Spannungsquelle für die Übertragungsfunktion.
Bei einer Rauschsimulation wird dieser Schaltungsteil abgetrennt und nur ein Widerstand mit dem Eingang des Operationsverstärkers Vin verbunden.
Beim praktischen Breadboard Aufbau rechts oben wurden 4 AA Batterien mit VP+ = 3 V und VP- = -3 V zur Spannungsversorgung (schwarzer Kasten rechts) eingesetzt.
Der minimale Rauscheffektivwert der Messung bei kleineren Widerstandswerten lag bei 14 mV.
Die Steigung der Ausgleichsgeraden von 0.0072 mV2 pro Ω
entspricht vu2 = 4 k T fbw R = 0.0069 mV2 R pro Ω in etwa dem erwarteten Wert.
Zur Messung der Verstärkung und des Frequenzganges wurde ein externes Sinus- und Rauschsignal mit einem Spannungsteiler (20 kΩ, 100 Ω) von 50 mV Amplitude auf 250 µV (Faktor 200) heruntergeteilt.
Mit einer Aluminiumabschirmung konnte für 200kΩ ein Schwingen des Ausgangssignals bei grossen Widerstandswerten vermieden werden.
Bei der Verwendung eines doppelten Spannungsteilers von 10kOhm und 100 Ohm, hatte die Übertragungsfunktion zwischen 1 kHz und 10 kHz eine zu kleine Verstärkung (Kapazitäten, Leckstrom).
Größere Verstärkung (10 statt 2) beim Filter führten auch zum Schwingen.
Es fehlen noch Bufferkapazitäten bei der Spannungsversorgung.
Das Oszilloskop des Electronic Explorers wurde mit einer Empfindlichkeit von 100mV/div und einer Zeitbasis von 1ms/div verwendet und der AC RMS Wert abgelesen.
Widerstandsrauschen
|
\( U_{rR}^2 (f) = 4 k T R \) \( U_{rR,rms}^2 = 4 k T R \Delta f \) \( U_{rR,rms} = \sqrt{4 k T R \Delta f} \) k = 1.38 · 10 -23 J/K T = 300 K Spannungswerte haben eine Gaussverteilung Vpp = 6.6 Vrms (Cresting factor, Scheitelfaktor) Simulation Rauschen mit FFT in Javascript |
Beispiel: Δ f = 10 kHz
Kann man \( U_{rR,rms}^2 \propto R \) messen |
Temperatur bewirkt als thermische Energie eine Bewegung der Ladungsträger in einem Widerstand und erzeugt eine messbare Spannung.
Dabei gilt die obige Formel für den Effektivwert.
Die Spannng ist abhängig von der Temperatur T, dem Widerstand R und der Bandbreite Δ f.
Bei bekanntem Widerstand, Temperatur und Bandbreite kann man die Boltzmann Konstante bestimmen.
Bei Änderung des Widerstandes oder der Temperatur kann man die Formel für den Rauschspannungseffektivwert bestätigen.
Die Tabelle zeigt typische Größenordnungen von Rauschspannungen, Rauschspannungsdichten und peak to peak Werten im µ V Bereich.
Aufgrund der Gaussverteilung gemessener Spannungswerte ergibt sich der Cresting Faktor von 6.6.
Dazu wurde eine JavaScript Simulation durchgeführt ( Simulation Rauschen mit FFT in Javascript).
Kann man die Eigenschaften von weissen Rauschen mit einer Simulation bestätigen?
1. Versuch
Zufallszahlen erzeugt mit Math.random() 0..1
Erzeugung der FFT und des Histogramms
2. Versuch
Erzeugung der FFT mit zufälliger Phase
Erzeugung der Zeitdaten und des Histogramms.
Gaussverteilung, Vpp = 6.6 Vrms (Cresting factor, Scheitelfaktor)
Spektrum und Noise Density
Ein Spektrum verteilt den Effektivwert auf NFFT einzelne Frequnezen.
Ein Spektrum normiert die Spectral Density mit 1 Hz.
Ae = 20 log(en)
Effektivwert vom Spektrum:
Ae + 20 * log(NFFT/2)
Widerstandsrauschen
|
\( U_{nR} = \sqrt{4 k T R BW} \) \( U_{nR} = 0.128 \frac{nV}{\sqrt{\Omega Hz}}\sqrt{R BW} \) \( BW = \frac{\pi}{2} f_{3dB} \) Es wird die Bandbreite BW eines Tiefpasses mit dem Faktor \( \frac{\pi}{2} \) zu Grunde gelegt. |
Die Grafik zeigt den Zusammenhang und typische Werte von Bandbreite, Widerstand und Rauscheffektivwert.
Ein Widerstand von 1 MOhm hat bei einer Bandbreite von 100 Hz eine
Rauschspannung größer 1 uV.
Thermisches Rauschen und Nyquist-Formel: Messungen (Lokal)
Thermisches Rauschen und Nyquist-Formel: Messungen (Lokal)
| R / Ω | BW / Hz | UnR / V |
| 10 k | 10 k | 1.28 µ |
| 1 M | 10 k | 12.8 µ |
Messschaltung: Operationsverstärkerschaltungsdimensionierung
Die Schaltung soll preisgünstig sein.
Man benötigt einen Verstärker (hohe Verstärkung, mehrere Stufen) mit Bandpass.
Die Eingangsspannungsrauschdichte des Operationsverstärkers muss kleiner als die Widerstandsrauschspannungsdichte sein.
Der Effektivwert soll mit einem Oszilloskop (oder True RMS Multimeter) gemessen werden.
LTSPICE Simulation
Die Simulation bildet die realisierte Schaltung ab.
Links sieht man den Spannungsteiler (R2, R17, R16) zur Bestimmung der Übertragungsfunktion.
Der Operationsverstärker TLC272 wird mit einer Verstärkung von vu1 = 48 und vu2 = 23 in nichtinvertierender Konfiguration verwendet.
Dabei wird die Bandbreite nicht zu sehr reduziert.
Die Widerstandswerte könnten noch reduziert werden, um den Beitrag zum Rauschen zu minimieren.
Der Stromverbrauch der Schaltung würde sich erhöhen.
Danach kommt ein Hochpass (fg = 1.6 kHz) und ein Tiefpass (fg = 16 kHz) mit jeweils einer Verstärkung von vu3 = vu4 = 2.
vu = vu1 · vu2 · vu3 · vu4 = 4416
Man verbindet den Vin1 Ausgang (R16/R17) mit dem Operationsverstärkereingang.
Man stellt V(V1), V(vout1), V(vout2), V(vout3) und V(vout4) dar und bestimmt Verstärkung und Eckfrequenzen.
Ein Widerstand von 100 kΩ ergibt einen Effektivwert am Ausgang (< STR > click auf das Label) von 30 mV.
Ein Widerstand von 10 kΩ ergibt einen Effektivwert am Ausgang (< STR > click auf das Label) von 18.4 mV.
Eine Änderung der Bandbreite auf 100 Hz bis 200kHz ergibt 19.5 mV.
Links sieht man den Spannungsteiler (R2, R17, R16) zur Bestimmung der Übertragungsfunktion.
Der Operationsverstärker TLC272 wird mit einer Verstärkung von vu1 = 48 und vu2 = 23 in nichtinvertierender Konfiguration verwendet.
Dabei wird die Bandbreite nicht zu sehr reduziert.
Die Widerstandswerte könnten noch reduziert werden, um den Beitrag zum Rauschen zu minimieren.
Der Stromverbrauch der Schaltung würde sich erhöhen.
Danach kommt ein Hochpass (fg = 1.6 kHz) und ein Tiefpass (fg = 16 kHz) mit jeweils einer Verstärkung von vu3 = vu4 = 2.
vu = vu1 · vu2 · vu3 · vu4 = 4416
Simulation Übertragungsfunktion (.ac)
.ac im Bereich von 1kHz bis 20 kHz.Man verbindet den Vin1 Ausgang (R16/R17) mit dem Operationsverstärkereingang.
Man stellt V(V1), V(vout1), V(vout2), V(vout3) und V(vout4) dar und bestimmt Verstärkung und Eckfrequenzen.
Simulation Rauschen (.noise)
.noise im Bereich von 1kHz bis 20 kHz.Ein Widerstand von 100 kΩ ergibt einen Effektivwert am Ausgang (< STR > click auf das Label) von 30 mV.
Ein Widerstand von 10 kΩ ergibt einen Effektivwert am Ausgang (< STR > click auf das Label) von 18.4 mV.
Eine Änderung der Bandbreite auf 100 Hz bis 200kHz ergibt 19.5 mV.
Simulationswerte
Tabelle
| R / Ohm | Urms (Uout4) / mV | Uout4pp = 6.6 Uout / mV |
| 100 | 16.4 | 109 |
| 1 000 | 16.6 | 110 |
| 4 700 | 17.4 | 115 |
| 10 000 | 18.4 | 121 |
| 20 000 | 20.1 | 133 |
| 47 000 | 24.2 | 160 |
| 100 000 | 30.6 | 202 |
| 470 000 | 58.3 | 385 |
| 1 000 000 | 83.2 | 549 |
Messaufbau

In einer mit Aluminium ausgekleideten Pappschachtel liegt das Breadboard.
Links ist der Spannungsteiler realisiert. Der erste TLC272 realisiert die ersten 2 Verstärkerstufen. Der zweite TLC272 realisiert Hochpass und Tiefpass.
Das Signal des Widerstandsrauschens darf nach der Verstärkung den Ausgangsspannungsbereich des Operationsverstärkers nicht überschreiten.
vrnoiserms * 6.6 * vu < VB+
\( v_{rnoiserms} = \sqrt{4 k T R fbw} = \sqrt{4 k T 100 k\Omega 20 kHz} = 5.8 \mu V\)
vu = 4461
VB+ = 3 V
169 mV < 3V
Laborgeräte:
Electronic Explorer
Seitenschneider
True RMS Voltmeter (Bild, Bezeichnung)
4x AA Batteriehalter mit Batterien und Mittenanschluss
Teileliste (Verbrauchsmaterial):
Breadboard
Kabelsortiment
2x TLC272
Schaltungswiderstände 1%: 2x 100 Ohm, 12x 10 kOhm, 230 kOhm, 470 kOhm
Messwiderstände: (1 kOhm, 4k7 Ohm,) 10 kOhm, 22 kOhm, 47 kOhm, 100 kOhm, (220 kOhm, 470 kOhm, 1 MOhm)
Filterkondensatoren: 2x 1nF, 2x 10nF
Blockkapazitäten:
Pappschachtel
Aluminiumfolie
Das Breadboard hat Beschriftungen für Zeilen (A..J) und Spalten (0..60), so dass Messpunkte oder externe Verbindungen spezifiziert werden können.
Top+(J33): VP+ (3 V), TOP-(J32): GND, Bottom+(J32): GND, Bottom-(J31): VP- (-3 V)
Signal out Vout4: C22, Vout3: B20, Vout2: B8
Signal in: A4 und Verbindung Draht H0, I9
Test Resistor: Bottom+ und I9

Links ist der Spannungsteiler realisiert. Der erste TLC272 realisiert die ersten 2 Verstärkerstufen. Der zweite TLC272 realisiert Hochpass und Tiefpass.
Das Signal des Widerstandsrauschens darf nach der Verstärkung den Ausgangsspannungsbereich des Operationsverstärkers nicht überschreiten.
vrnoiserms * 6.6 * vu < VB+
\( v_{rnoiserms} = \sqrt{4 k T R fbw} = \sqrt{4 k T 100 k\Omega 20 kHz} = 5.8 \mu V\)
vu = 4461
VB+ = 3 V
169 mV < 3V
Laborgeräte:
Electronic Explorer
Seitenschneider
True RMS Voltmeter (Bild, Bezeichnung)
4x AA Batteriehalter mit Batterien und Mittenanschluss
Teileliste (Verbrauchsmaterial):
Breadboard
Kabelsortiment
2x TLC272
Schaltungswiderstände 1%: 2x 100 Ohm, 12x 10 kOhm, 230 kOhm, 470 kOhm
Messwiderstände: (1 kOhm, 4k7 Ohm,) 10 kOhm, 22 kOhm, 47 kOhm, 100 kOhm, (220 kOhm, 470 kOhm, 1 MOhm)
Filterkondensatoren: 2x 1nF, 2x 10nF
Blockkapazitäten:
Pappschachtel
Aluminiumfolie
Realisierte Schaltung
>Das Breadboard hat Beschriftungen für Zeilen (A..J) und Spalten (0..60), so dass Messpunkte oder externe Verbindungen spezifiziert werden können.
Top+(J33): VP+ (3 V), TOP-(J32): GND, Bottom+(J32): GND, Bottom-(J31): VP- (-3 V)
Signal out Vout4: C22, Vout3: B20, Vout2: B8
Signal in: A4 und Verbindung Draht H0, I9
Test Resistor: Bottom+ und I9

Messungen
- Die Übertragungsfunktion mit einem Eingangssinussignal
liefert Bandbreite und Verstärkung
Da der Funktionsgenerator nur eine minimale Amplitude von 100 mV erlaubt, muss das Eingangssignal heruntergeteilt (:200)werden. - Erzeugung einer Rauschspannung mit dem Funktionsgenerator und Messung des Ausgangseffektivwertes.
- Bestimmung der Frequenz- und Amplitudeneinstellung des Funktionsgenerators
- Bestimmung der Zeitbasis (10ms/div) und der Auflösung (100mV/div) des Oszilloskops
- Messung des Effektivwertes AC RMS verschiedener Widerstände
- Messung der rms Spannung mit einem True RMS Multimeter
- Vergleich von Messung, Simulation und Theorie
Messergebnis Übertragungsfunktion
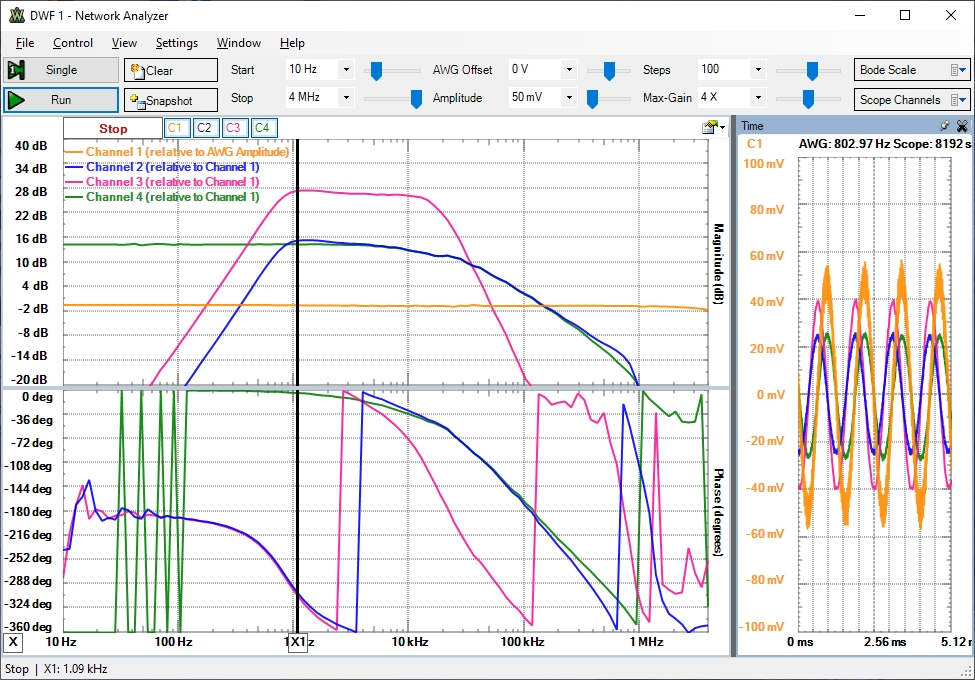
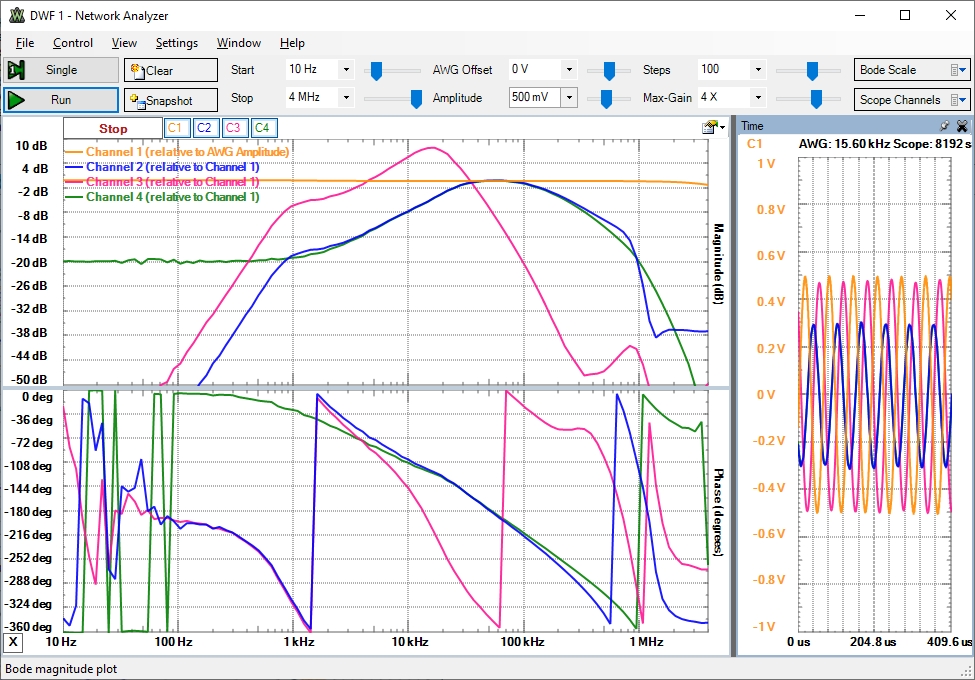
Einfacher Spannungsteiler 20 kOhm, 100 Ohm.
Die Ausgangsspannung wird von der Versorgungsspannung limitiert.

Doppelter Spannungsteiler 10 kOhm, 100 Ohm.
Die Delle in der Übertragungsfunktion zwischen 1 kHz bis 5/10 kHz kommt vom doppelten Spannungsteiler. Parallel zu den Widerständen liegt ein kapazitiver Teiler mit der Eingangskapazität des Operationsverstärkers vor.
Der größte Beitrag der Übertragungsfunktion liegt zwischen 10..15 kHz.
Messergebnis Rauschquelle
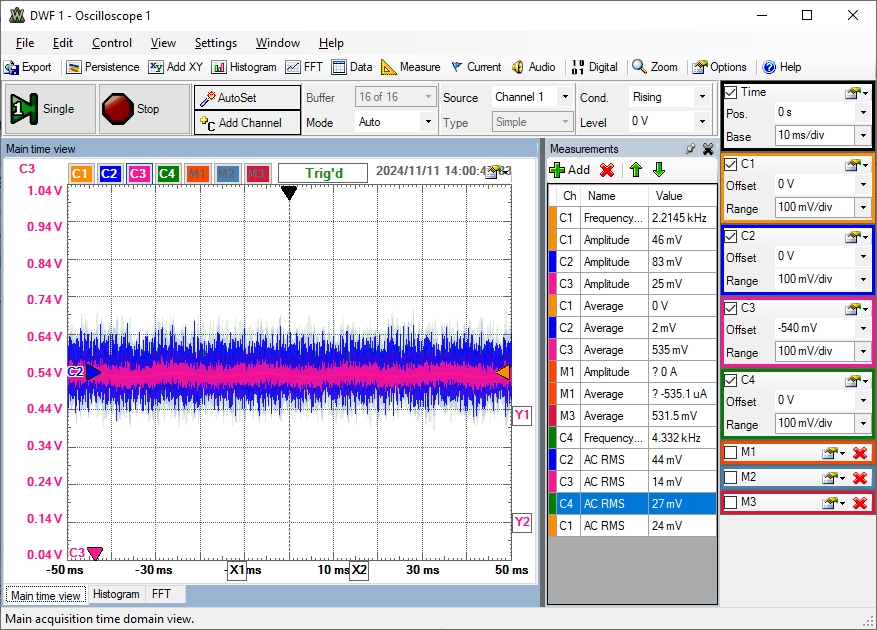 |
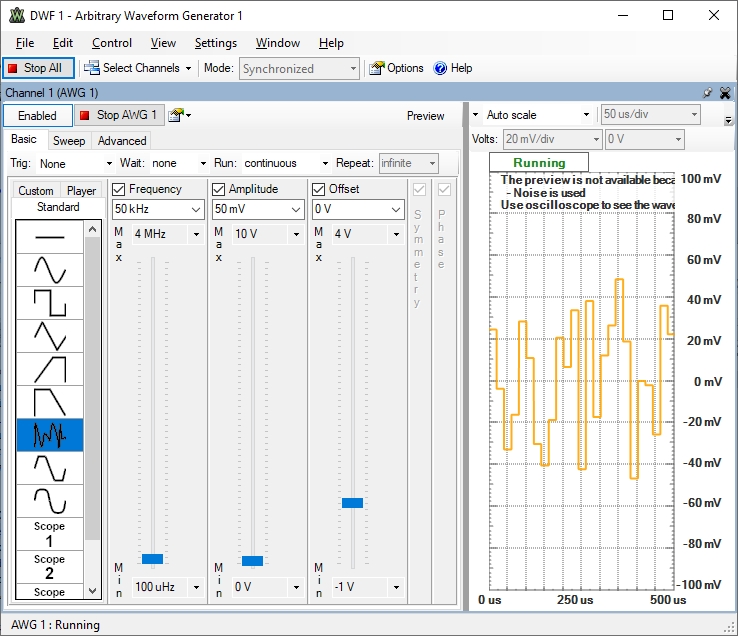 |
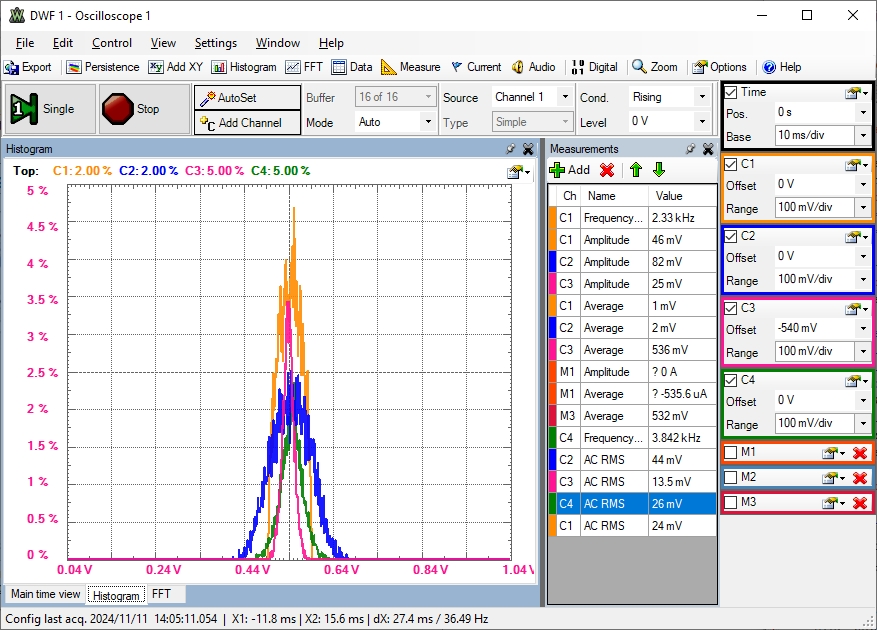
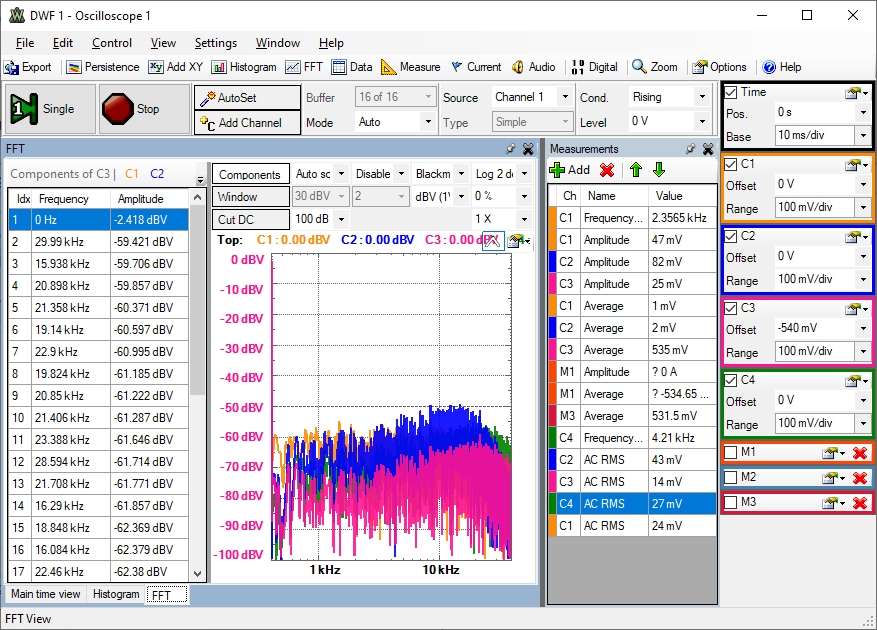
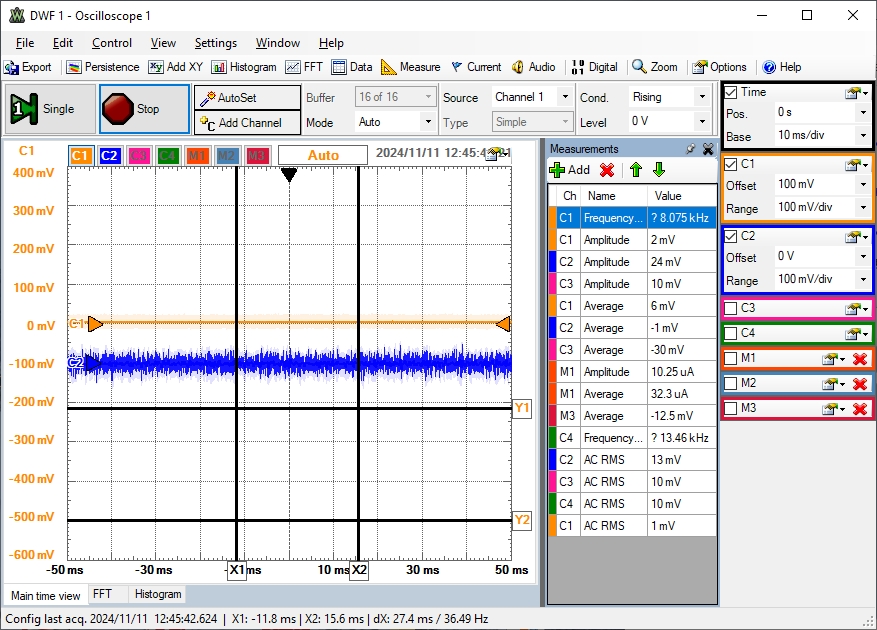
Im Oszilloskopbild (10 ms/div) sieht man die AC Effektivwerte:
C1(Quelle) 24 mV, C3(x48*22) 14 mV, C4 (HP,2) 27 mV, C2(HP,LP,4) 44 mV
100mV
C1(Quelle) 50 mV, C3(x48*22) 26 mV, C4 (HP,2) 54 mV, C2(HP,LP,4) 86 mV
200mV
C1(Quelle) 100 mV, C3(x48*22) 54 mV, C4 (HP,2) 108 mV, C2(HP,LP,4) 170 mV
 |
 |
 |
Messergebnis Oszilloskopbild
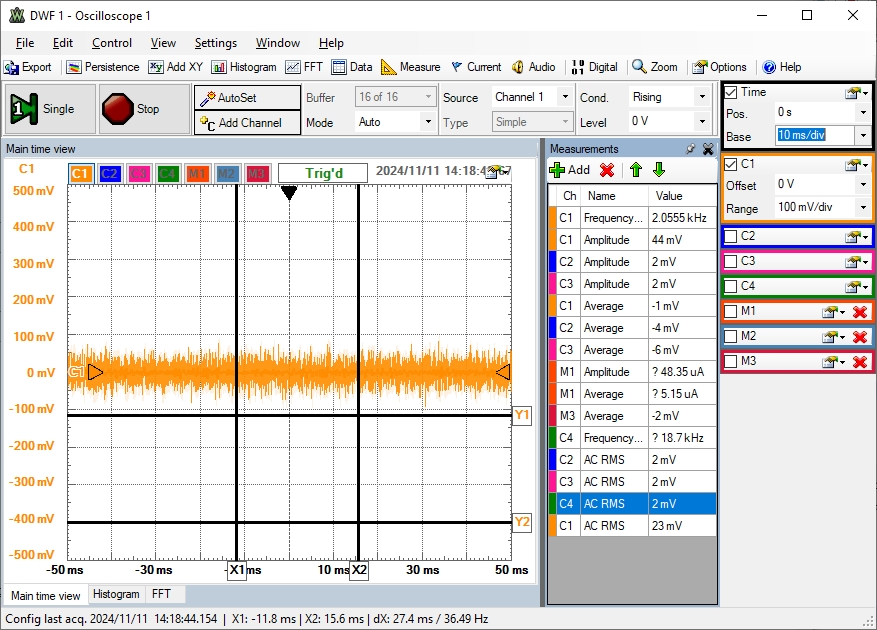
Das Bild zeigt die Messung (C1, Ausgang des Verstärkers) für den 47 kOhm Widerstand mit C1(AC RMS) = 23 mV.
Messwerte
Tabelle und Kurve
| R / Ohm | Urms (Uout4) / mV | Urms2 / mV2 | True RMS meter / mV | |
| 1000 | 14 | 196 | .. | |
| 4700 | 14 | 196 | 14.3 | |
| 10000 | 16 | 256 | 15.3 | |
| 20000 | 18 | 324 | 17.8 | |
| 47000 | 24 | 576 | 25.5 | |
| 100000 | 30 | 900 | 32.5 | geerdetes Gehäuse |
| 100000 | 47 | ohne geerdetes Gehäuse |
Steigung der gemessenen Ausgleichsgeraden:
0.0072 mV2 S = 7.2 10-9 V S
4 k T fbw vu = 6.55 -9 V S
Die Steigung ist in der selben Größenordnung wie der theoretische Wert.
Unterhalb von 1 kOhm ist das Widerstandsrauschsignal zu klein
und man misst das Rauschen der Schaltung.
Oberhalb von 100 kOhm schwingt die Schaltung und man bekommt am Ausgang nur die maximalen Spannungen.
Mit der geerdeten Alufolie als Abschirmung setzt das Schwingen erst oberhalb von 200 kOhm ein.

Agilent U1233A True RMS Multimeter
Oberhalb von 100 kOhm schwingt die Schaltung und man bekommt am Ausgang nur die maximalen Spannungen.
Mit der geerdeten Alufolie als Abschirmung setzt das Schwingen erst oberhalb von 200 kOhm ein.

Agilent U1233A True RMS Multimeter
Zusammenfassung Widerstandsrauschmessung
- Theorie, Simulation und Messung passen gut zusammen
- Der Rauschmessbereich ist von
Rmin = 10k bis Rmax 100k,
und Vnoisemin = 13.5 nV/Hz0.5 bis Vnoisemax = 41 nV/Hz0.5
eingeschränkt - Den Effektivwert am Ausgang kann man auch mit einem True RMS Multimeter messen
Weitere Untersuchungen
Quellen:
Thermisches Rauschen und Nyquist-Formel: Messungen (Lokal)
- Messung der Operationsverstärkereingangsrauschspannung
- Ausweitung des Messbereichs von 10 kOhm..100 kOhm zu 100 Ohm.. 1 MOhm
- Vergrößerung der Gesamtverstärkung
- Verkleinerung der Widerstandswerte der Rückkoppelung
- Messung der Temperaturabhängigkeit
- Veränderung der Bandbreite
- Vergleich Spannungsquelle Batterie versus Spannungsgenerator
- Einfluss von Bufferkapazitäten
Quellen:
Thermisches Rauschen und Nyquist-Formel: Messungen (Lokal)