Grundlagen Elektrotechnik 2
05 Komplexe Darstellung sinusförmiger Wechselgrößen
Prof. Dr. Jörg Vollrath
Rückblick und Heute
LTSPICE
- Programmeinrichtung, Schaltungselemente, Analysearten
- Simulation, Auswertung, Parameter, Netzliste
Heute:
- Lernmethoden
- Sinusgrößen unterschiedlicher Frequenz
- Überlagerung von Sinusgrößen
- Zeigerdarstellung
Sinusgrößen unterschiedlicher Frequenz
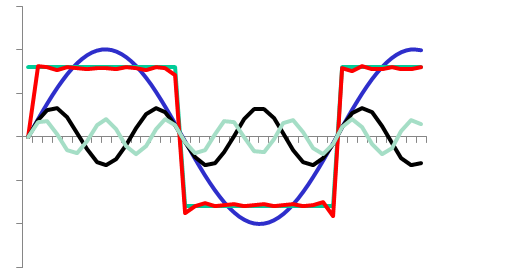
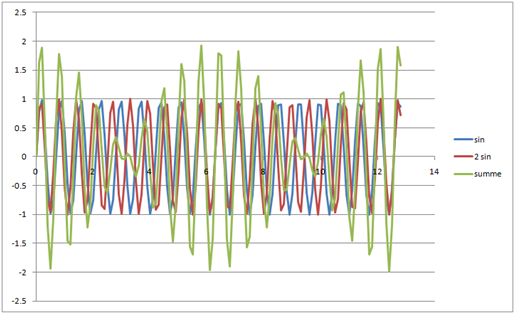
\( u(t) = \hat{u}_1 cos(\omega_1 t + \phi_{u1})
+ \hat{u}_2 cos(\omega_2 t + \phi_{u2} ) \)
|
|
Überlagerung von Sinusgrößen gleicher Frequenz
\( u(t) = u_1 (t) + u_2 (t) \)
| \( u(t) = \hat{u} cos ( \omega t \phi_u ) \) | \( u(t) = \hat{u}_1 cos ( \omega t \phi_{u1} ) + \hat{u}_2 cos ( \omega t \phi_{u2} ) \) |
\( u(t) = \hat{u} ( cos \phi_u cos \omega t - sin \phi_u sin \omega t ) \)
\( u(t) = \hat{u}_1 ( cos \omega t cos \phi_{u1} - sin \phi_{u1} sin \omega t ) + \hat{u}_2 ( cos \omega t cos \phi_{u2} - sin \phi_{u2} sin \omega t ) \)
\( u(t) = ( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} ) cos \omega t ) - ( \hat{u}_1 sin \phi_{u1} ) sin \omega t ) \)
Koeffizientenvergleich für \( sin \omega t \) und \( cos \omega t \) :
(1) \( \hat{u} cos \phi_u = \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \)
(2) \( \hat{u} sin \phi_u = \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \)
Bestimmung des Winkels aus dem Quotienten \( \frac{(1)}{(2)} \):
\( \frac{\hat{u} sin \phi_u}{\hat{u} cos \phi_u} = \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}} \)
\( \phi_u = arctan \left( \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}} \right) \)
Bestimmung der Amplitude aus \( (1)^2 + (2)^2 \)
\( \left( \hat{u} cos \phi_u \right)^{2} + \left( \hat{u} sin \phi_u \right)^{2} = \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2} \)
\( \hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2} } \)
\( \hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1}\right)^{2} + \left( \hat{u}_2 cos \phi_{u2} \right)^{2} + 2 \hat{u}_1 cos \phi_{u1} \hat{u}_2 cos \phi_{u2} + \left( \hat{u}_1 sin \phi_{u1} \right)^{2} + \left( \hat{u}_2 sin \phi_{u2} \right)^{2} + 2 \hat{u}_1 sin \phi_{u1} \hat{u}_2 sin \phi_{u2} } \)
\( sin^{2} \phi + cos^{2} \phi = 1 \)
\( cos \alpha cos \beta + sin \alpha sin \beta = cos ( \alpha - \beta) \)
\( \hat{u} = \sqrt{ \left( \hat{u}_1 \right)^{2} + \left( \hat{u}_2 \right)^{2} + 2 \hat{u}_1 \hat{u}_2 cos(\phi_{u2} - \phi_{u1}) } \)
Beispiel: Überlagerung von Sinusgrößen gleicher Frequenz
Zwei Quellen mit sinusförmiger Quellenspannung gleicher Frequenz sind in Reihe geschaltet.
\( \hat{u}_{q1} = 50 V; \phi_{u1} = 80°; f_1 = 50 Hz; \) \( \phi = \frac{80°}{180°} \cdot \pi = 1.3298 \)
\( \hat{u}_{q2} = 30 V; \phi_{u2} = 15°; f_2 = 50Hz; \)
Simulieren Sie mit SPICE und berechnen Sie die Amplitude und den Nullphasenwinkel der Klemmenspannung und zeichnen Sie die Liniendiagramme sämtlicher Spannungen. \( \hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2} } \)
\( \hat{u} = \sqrt{ \left( 37.66 V \right)^{2} + \left( 57 V \right)^{2} } = 63.5 V \)
\( \phi_u = arctan \left( \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}} \right) = 50.92° \)
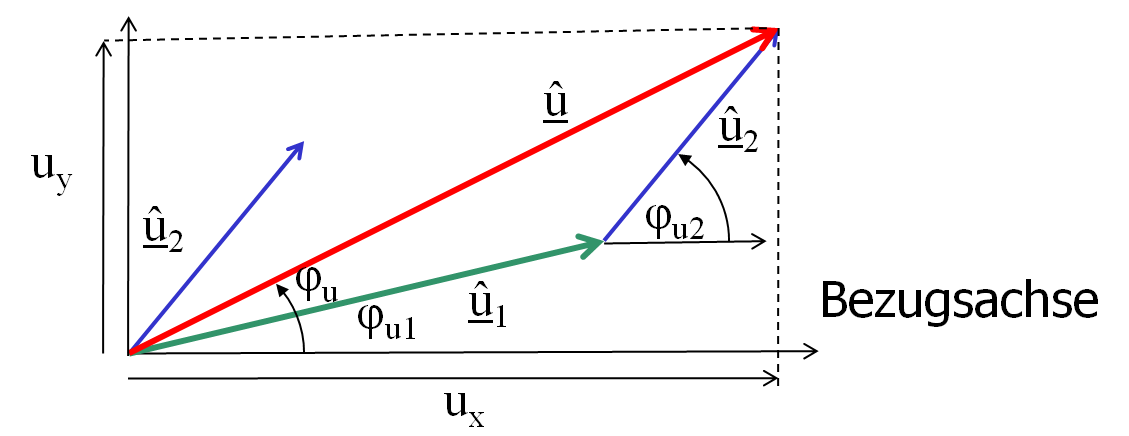
Zeigerdarstellung

|
Addition im Zeigerdiagramm
- Normierung
Eine Spannung(Strom) wird mit einem Skalierungsfaktor in eine Länge(cm) umgerechnet, damit alle Größen bei der Zeichnung auf ein Blatt passen. - Der erste Zeiger wird angetragen.
- Bei einer Addition wird der Anfang(Fuß) des nächsten Zeigers an das Ende(Spitze) des ersten Zeigers angesetzt.
- Bei einer Subtraktion wird die Richtung des Zeiger der subtrahiert wird umgedreht.
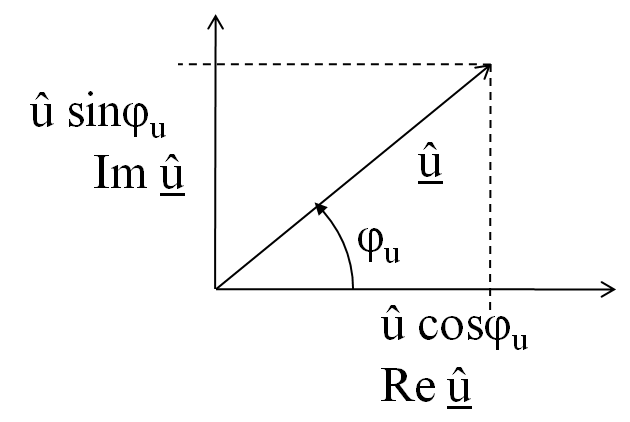
Komplexe Symbole
|
|