- Übersicht Grundlagen der Elektrotechnik 2
Prof. Dr.-Ing. Jörg Vollrath
Dies ist eine Vorlesung mit 4 SWS. 27 Vorlesungen a 90 Minuten.Grundlagen Elektrotechnik 2 (56 WS)
|
- Vorlesung Grundlagen der Elektrotechnik 2
16.03.2026
Kenngrößen: Periodizität, Frequenz f, Periodendauer T, Amplitude \( \hat{u} \)
\( f = \frac{1}{T} \)
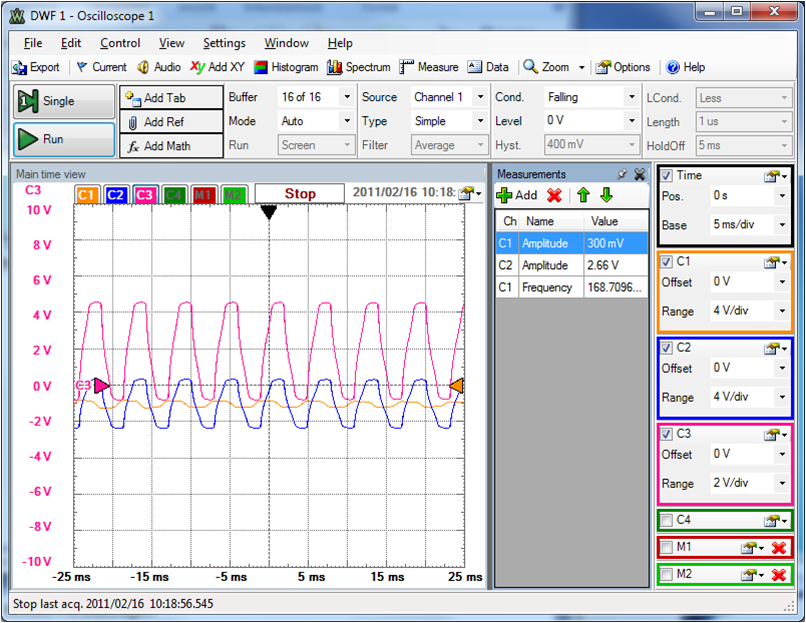
01. Wechselgrößen
Anwendungen: Ton, Generator, OszilloskopKenngrößen: Periodizität, Frequenz f, Periodendauer T, Amplitude \( \hat{u} \)
\( f = \frac{1}{T} \)
17.03.2026
\( \overline{u} = \frac{1}{T} \int_0^T u(t) dt \) \( U = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt} \) Geradengleichung
\( y = a x + b = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) + y_1 \)
02a. Wechselgrößen
Gleichwert, Effektivwert, Leistung\( \overline{u} = \frac{1}{T} \int_0^T u(t) dt \) \( U = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt} \) Geradengleichung
\( y = a x + b = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) + y_1 \)

18.03.2026
Numerische Integration (Excel, C, JavaScript)
\( \int_{0}^{T} f(t) dt = \frac{T}{n} \sum_{i=1}^{n} y_i (t_i) \)
Video:
Buch:
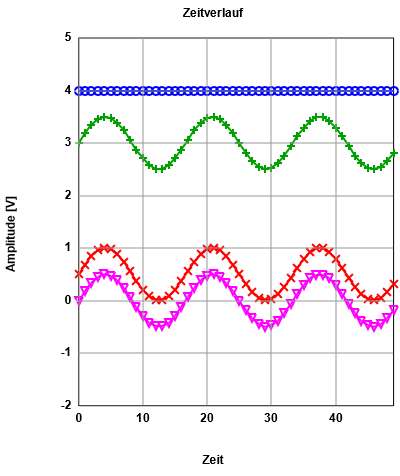
02b. Wechselgrößen
Mischgrößen, Kenngrößen Geradengleichung, IntegralrechnungNumerische Integration (Excel, C, JavaScript)
\( \int_{0}^{T} f(t) dt = \frac{T}{n} \sum_{i=1}^{n} y_i (t_i) \)
Video:
Buch:
23.03.2026
\( U(t) = \hat{u} sin(\omega t + \phi) \)
\( \omega = 2 \pi f \)
Formfaktor, Gleichrichtwert
Leiterschleife, Rechtecksignal
Buch:
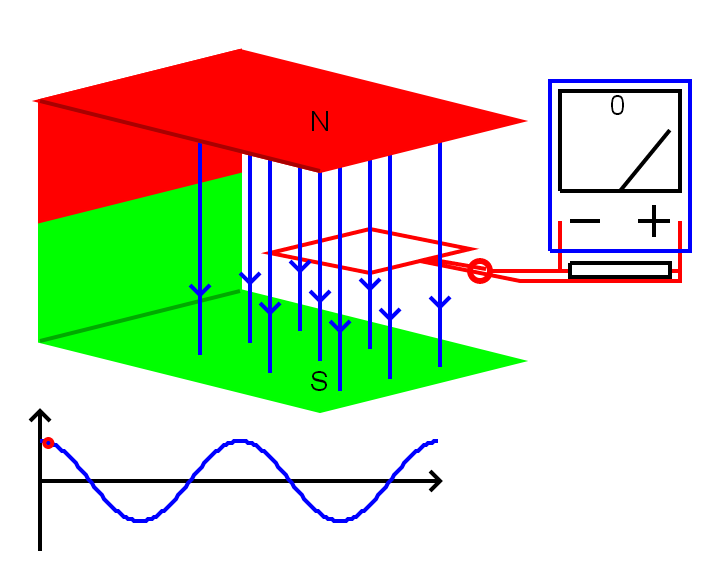
03a. Sinusförmige Wechselgrößen
Laborgeräte, Formel, Kreisfrequenz ω\( U(t) = \hat{u} sin(\omega t + \phi) \)
\( \omega = 2 \pi f \)
Formfaktor, Gleichrichtwert
Leiterschleife, Rechtecksignal
Buch:

24.03.2026
\( \overline{u} = 0 \) \( \overline{|u(t)|} = \frac{2 \hat{u}}{\pi} \) \( U = \frac{\hat{u}}{\sqrt{2}} = 0.7 \hat{u} \)
03b. Sinusförmige Wechselgrößen
Gleichwert, Gleichrichtwert, Effektivwert\( \overline{u} = 0 \) \( \overline{|u(t)|} = \frac{2 \hat{u}}{\pi} \) \( U = \frac{\hat{u}}{\sqrt{2}} = 0.7 \hat{u} \)
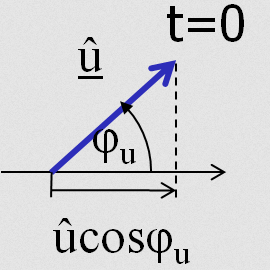
30.03.2026
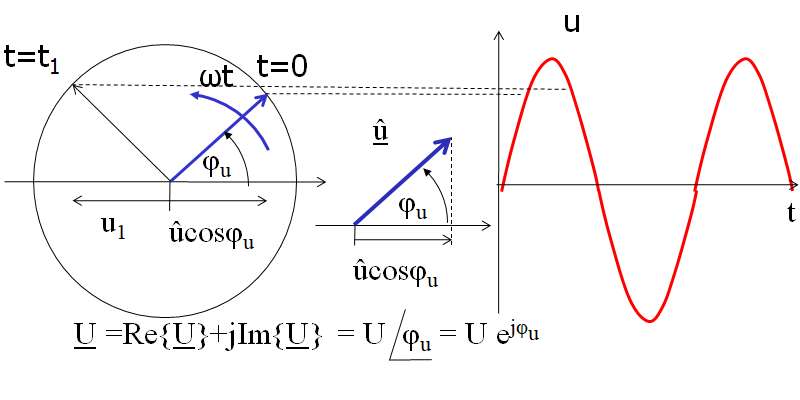
\( \underline{U} = U cos(\phi) + j U sin(\phi) = U e^{j \phi} \)
R-Form und P-Form
Video:
Buch:
05. Komplexe Darstellung
Zeigerdarstellung\( \underline{U} = U cos(\phi) + j U sin(\phi) = U e^{j \phi} \)
R-Form und P-Form
Video:
Buch:
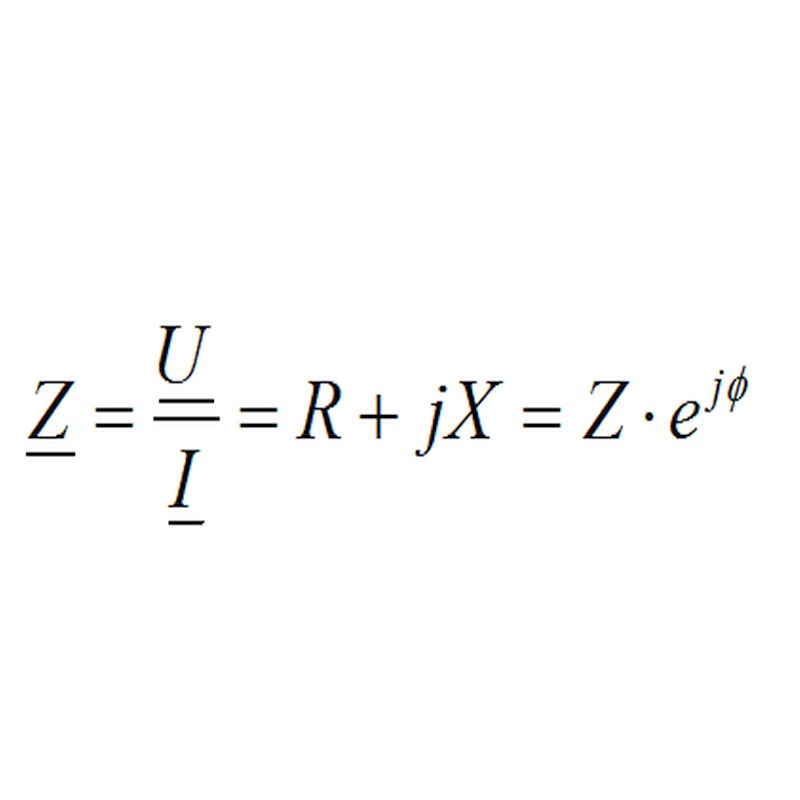
31.03.2026
\( \underline{Z} = \frac{\underline{U}}{\underline{I}} = R + jX = Z \cdot e^{j\phi} \)
Buch:
01.04.2026 Übung 1a: Effektivwert, LTSPICE
06. Komplexe Lineare Zweipole
Wirkwiderstand, Blindwiderstand\( \underline{Z} = \frac{\underline{U}}{\underline{I}} = R + jX = Z \cdot e^{j\phi} \)
Buch:
01.04.2026 Übung 1a: Effektivwert, LTSPICE
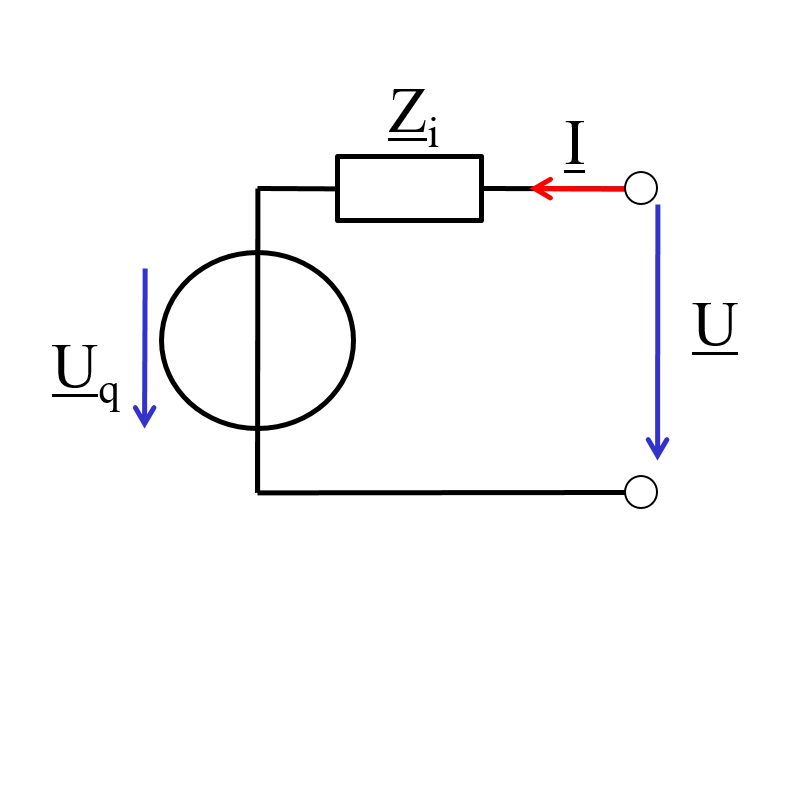
07.04.2026
\( \underline{U}_L = \underline{I}_K \cdot \underline{Z}_i \)
08.04.2026 Übung 1b: Effektivwert, LTSPICE
07. Ersatzquellen
Leerlaufspannung, Kurzschlußstrom, Innenwiderstand\( \underline{U}_L = \underline{I}_K \cdot \underline{Z}_i \)
08.04.2026 Übung 1b: Effektivwert, LTSPICE
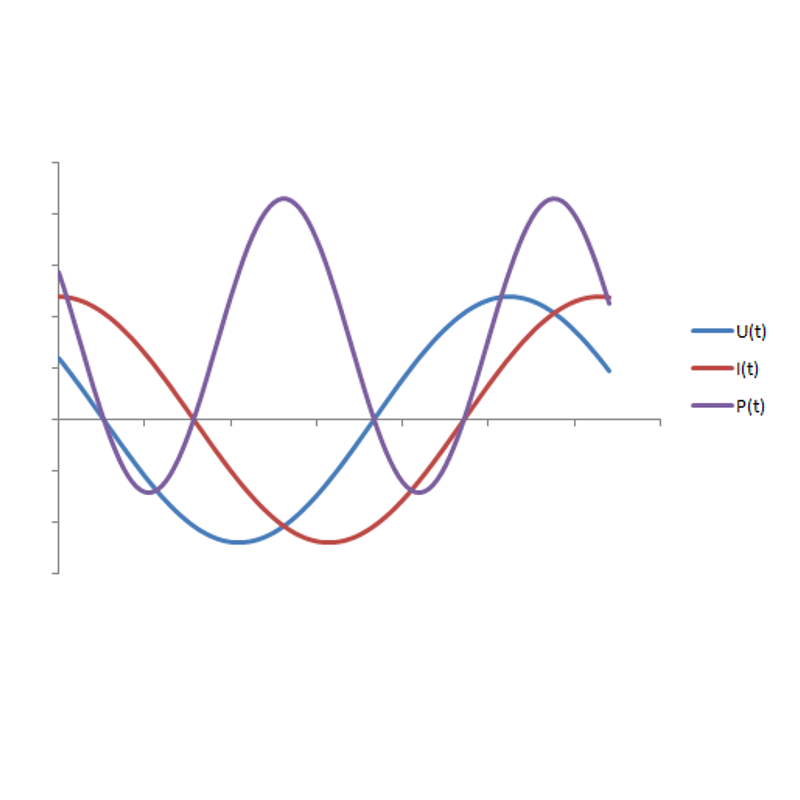
13.04.2026
\( \underline{S} = \underline{U} \cdot \underline{I}^* = P + j Q\)
Video:
Buch:
Start: Versuch P1 Zylinderspule
08. Leistung
Komplexe Leistung\( \underline{S} = \underline{U} \cdot \underline{I}^* = P + j Q\)
Video:
Buch:
Start: Versuch P1 Zylinderspule

14.04.2026
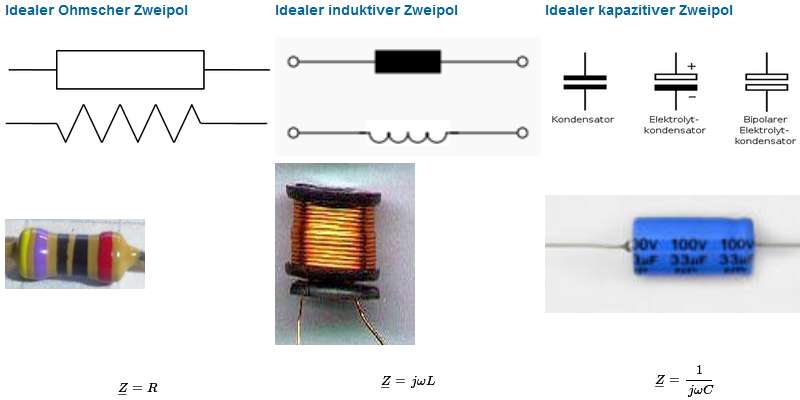
\( C = \frac{I dt}{d U} \) \( U = L \frac{dI}{dt} \)
Komplexer Widerstand und Leitwert
\( \underline{Z}_C = \frac{1}{j \omega C} = \frac{1}{\underline{Y}_C}\) \( \underline{Z}_L = j \omega L \)
15.04.2026 Übung 2a: Leistung, Quelle und Last
09. Kapazität und Induktivität
Differentialgleichung\( C = \frac{I dt}{d U} \) \( U = L \frac{dI}{dt} \)
Komplexer Widerstand und Leitwert
\( \underline{Z}_C = \frac{1}{j \omega C} = \frac{1}{\underline{Y}_C}\) \( \underline{Z}_L = j \omega L \)
15.04.2026 Übung 2a: Leistung, Quelle und Last
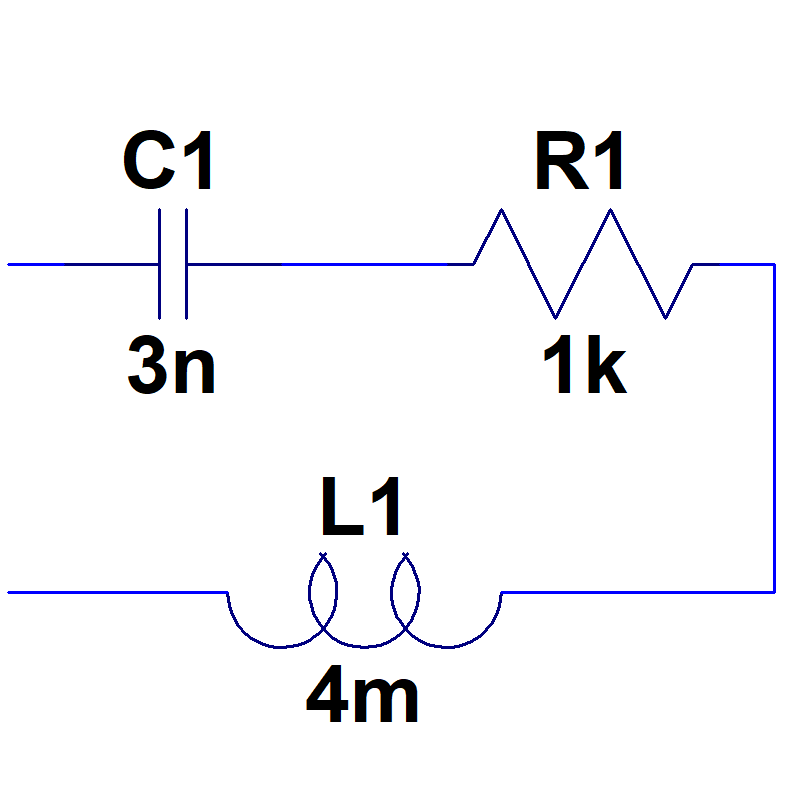
20.04.2026
\( \underline{Z} = \sum{\underline{Z}_i} \)
Stromgleichung des Spannungsteilers
\( \underline{I} = \frac{\underline{U}_1}{\underline{Z}_1} = \frac{\underline{U}}{\underline{Z}} \)
10. Reihenschaltung
Summe der komplexen Widerstände\( \underline{Z} = \sum{\underline{Z}_i} \)
Stromgleichung des Spannungsteilers
\( \underline{I} = \frac{\underline{U}_1}{\underline{Z}_1} = \frac{\underline{U}}{\underline{Z}} \)
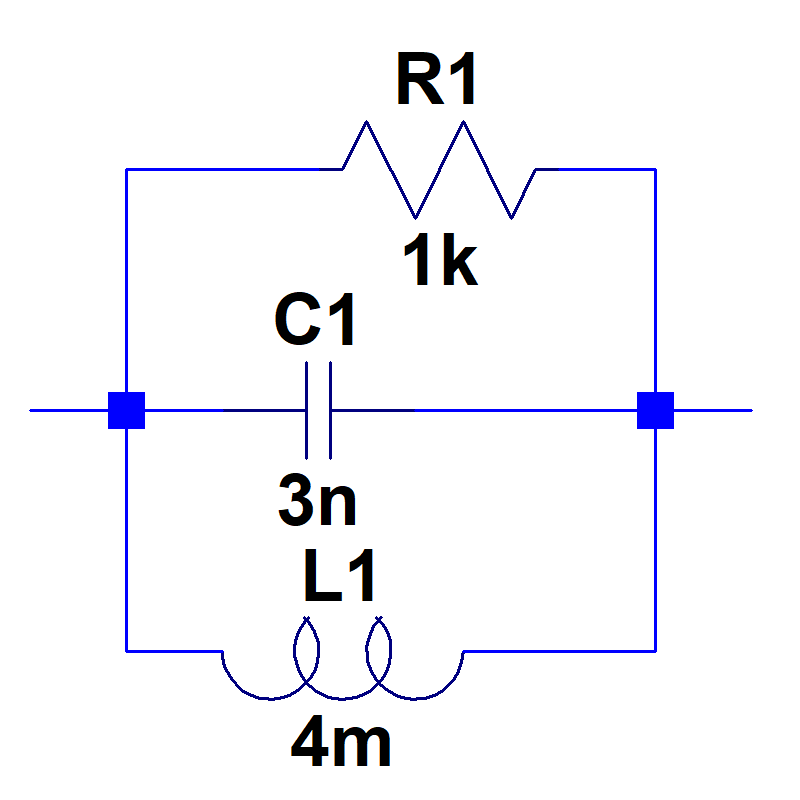
21.04.2026
\( \underline{Y} = \sum{\underline{Y}_i} = G + j B \)
21.04.2026 Übung 2b: Leistung, Quelle und Last
Video:
Buch:
11. Parallel
Summe der komplexen Leitwerte\( \underline{Y} = \sum{\underline{Y}_i} = G + j B \)
21.04.2026 Übung 2b: Leistung, Quelle und Last
Video:
Buch:
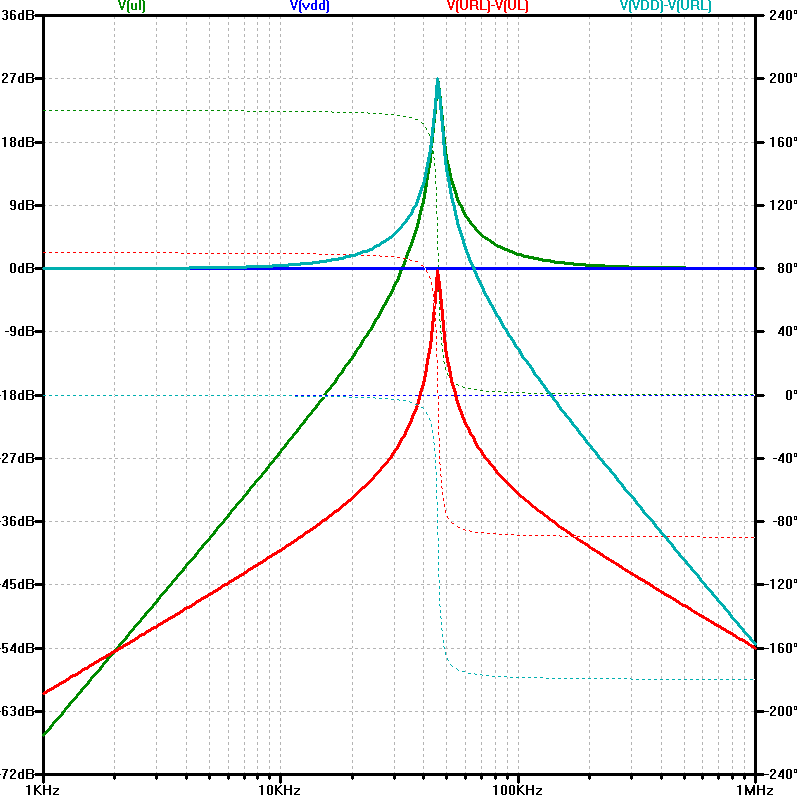
27.04.2026
Spannungsüberhöhung
\( K_U = \frac{U_C (w_r)}{U (w_r)} = \frac{U_L (w_r)}{U (w_r)} \)
Video:
Buch:
12. Resonanz
\( Im\{\underline{Z}\} = 0 \)Spannungsüberhöhung
\( K_U = \frac{U_C (w_r)}{U (w_r)} = \frac{U_L (w_r)}{U (w_r)} \)
Video:
Buch:
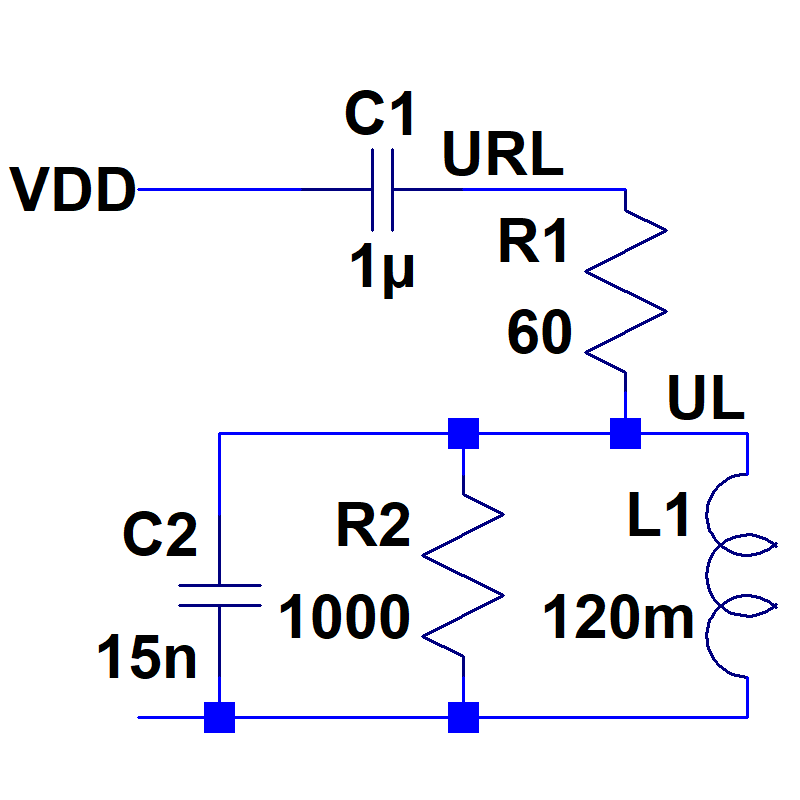
28.04.2026
29.04.2026 Übung 3
Video:
Start Versuch P2: Wechselstromschaltungen
13. Schwingkreis
Der Imaginärteil des gesamten komplexen Widerstands oder Leitwertes ist Null29.04.2026 Übung 3
Video:
Start Versuch P2: Wechselstromschaltungen
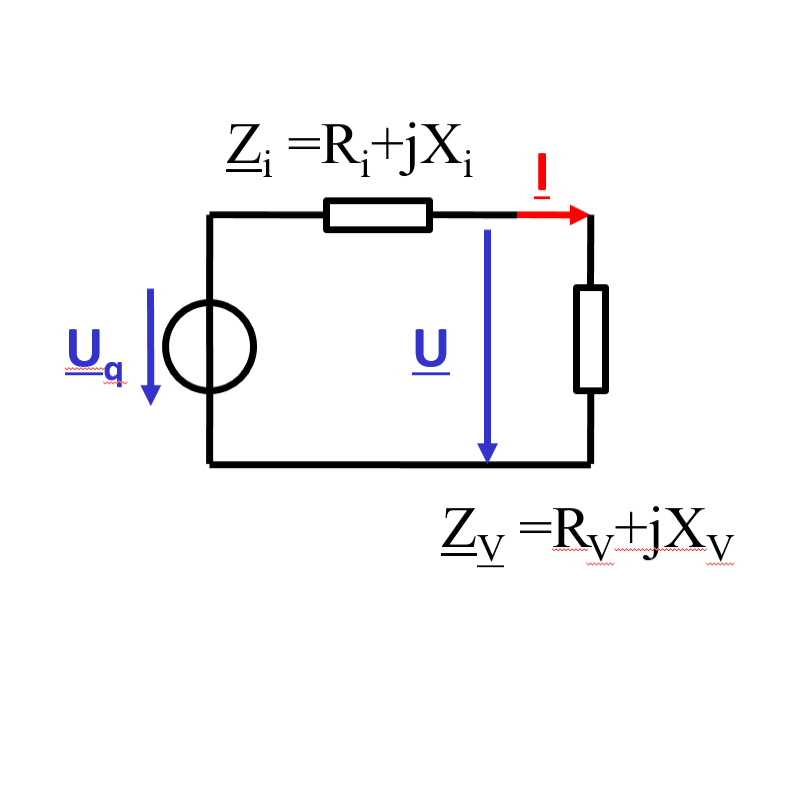
4.05.2026
Maximale Leistung:
\( P_{max} = \frac{U_q^2}{4 \cdot R_i} \)
Buch:
Video:
14. Leistungsanpassung
Ri = RL, Xi = ±XLMaximale Leistung:
\( P_{max} = \frac{U_q^2}{4 \cdot R_i} \)
Buch:
Video:
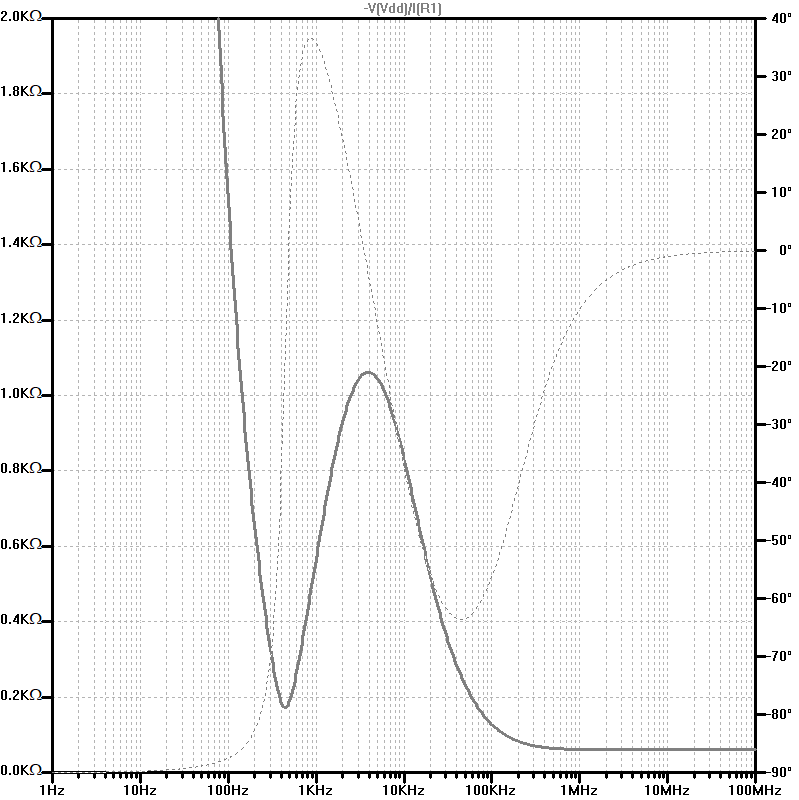
5.05.2026
\( \underline{z}(\Omega) = \frac{\underline{z}(\omega)}{R_{Bez}} \) Normierung: RBezug, \( \omega_{Bez} = \frac{\omega}{\Omega} \)
15. Unterschiedliche Frequenzen
Der frequenzabhängie normierte Widerstand\( \underline{z}(\Omega) = \frac{\underline{z}(\omega)}{R_{Bez}} \) Normierung: RBezug, \( \omega_{Bez} = \frac{\omega}{\Omega} \)
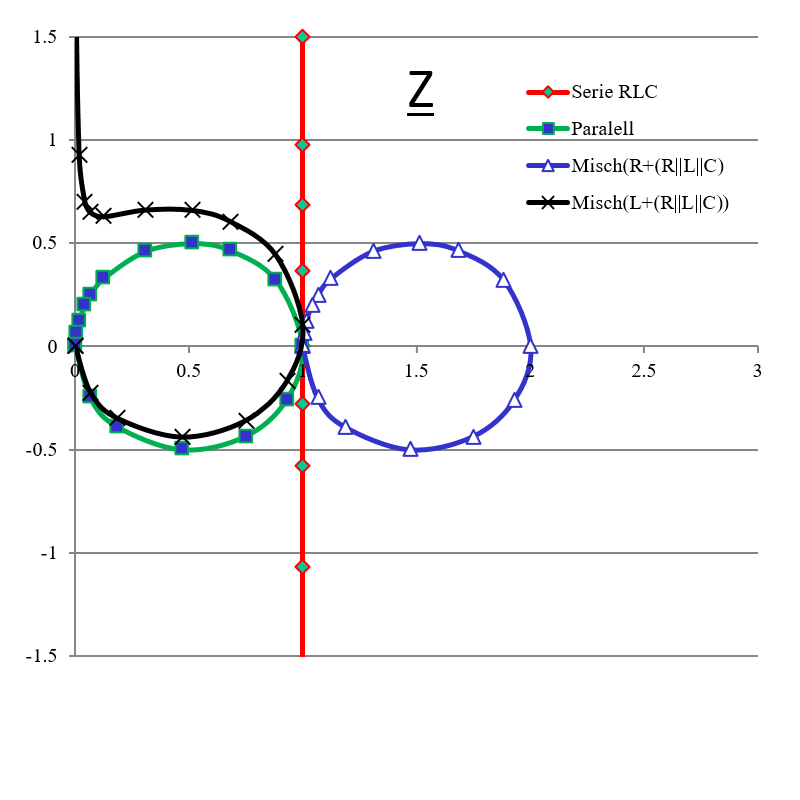
11.05.2026
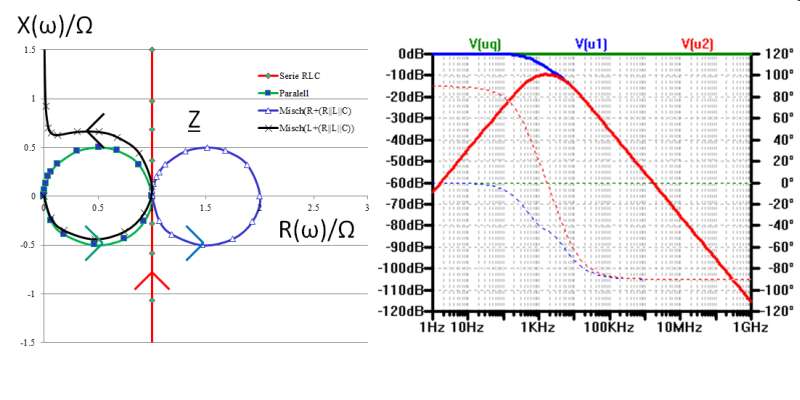
\( Re\{\underline{Z} (j\omega) \}, Im\{\underline{Z} (j\omega) \} \)
LTspice: AC Analyse
y-Achsen Skalierung
Nyquist plot
Video:
16. Ortskurven
Grafische Darstellung des Widerstandes\( Re\{\underline{Z} (j\omega) \}, Im\{\underline{Z} (j\omega) \} \)
LTspice: AC Analyse
y-Achsen Skalierung
Nyquist plot
Video:
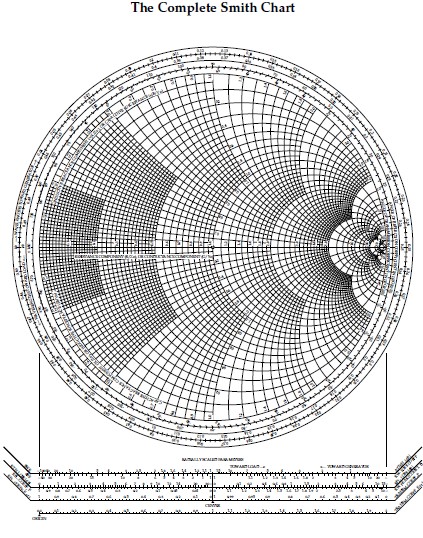
12.05.2026
\( \underline{W} (\underline{z}) = \frac{\underline{z}}{1 + \underline{z}} \)
Start Versuch P3: Oszilloskop
13.05.2026 Übung 4a: Komplexer Widerstand, Ortskurve, Bodediagramm
Buch:
17. Smith Chart
S-Parameter Analyzer, Moebiustransformation, Übertragungssysteme\( \underline{W} (\underline{z}) = \frac{\underline{z}}{1 + \underline{z}} \)
Start Versuch P3: Oszilloskop
13.05.2026 Übung 4a: Komplexer Widerstand, Ortskurve, Bodediagramm
Buch:
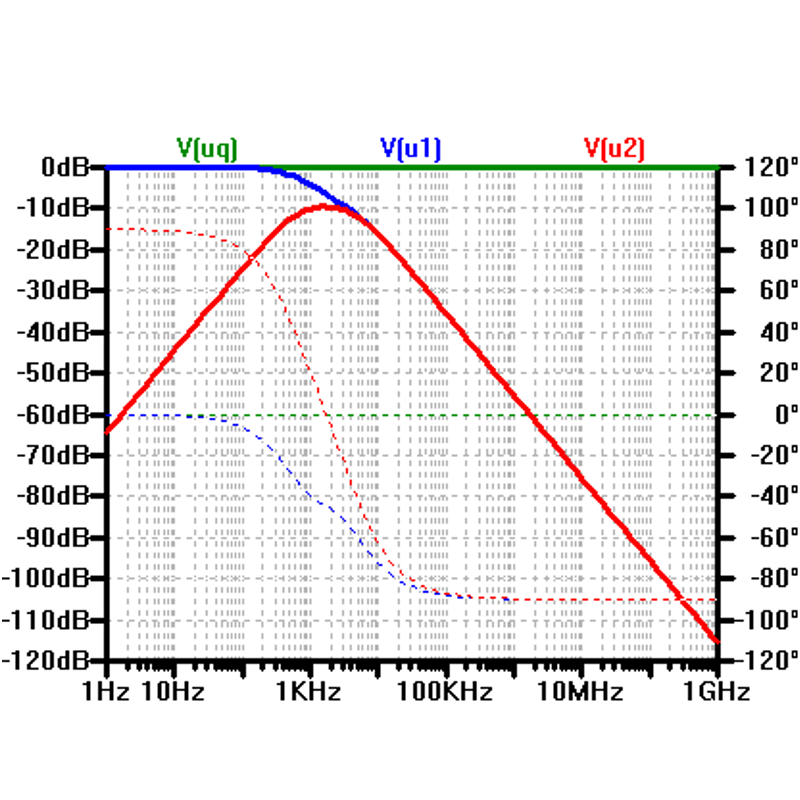
18.05.2026
Nullstellen Sn
Polstellen Sp
\( \underline{T} (j \omega) = \frac{\underline{U}_2 (j \omega)}{\underline{U}_1 (j \omega)} = K \frac{(j\omega - S_{N1})... } {(j\omega - S_{P1})...}\)
Ein Frequenzabhängiges Verhältnis von Spannung (Strom) wird untersucht.
Das Maß in Dezibel:
\( A(j \omega ) = 20 log | \underline{T} (j\omega)| \)
18a. Bodediagramm (1)
Komplexe Übertragungsfunktion:Nullstellen Sn
Polstellen Sp
\( \underline{T} (j \omega) = \frac{\underline{U}_2 (j \omega)}{\underline{U}_1 (j \omega)} = K \frac{(j\omega - S_{N1})... } {(j\omega - S_{P1})...}\)
Ein Frequenzabhängiges Verhältnis von Spannung (Strom) wird untersucht.
Das Maß in Dezibel:
\( A(j \omega ) = 20 log | \underline{T} (j\omega)| \)

19.05.2026
20.05.2026 Übung 4b: Komplexer Widerstand, Ortskurve, Bodediagramm
18b. Bodediagramm (2)
\( \underline{T} (j \omega) = \frac{\underline{U}_2 (j \omega)}{\underline{U}_1 (j \omega)} = K \frac{(j\omega - S_{N1})... } {(j\omega - S_{P1})...}\)20.05.2026 Übung 4b: Komplexer Widerstand, Ortskurve, Bodediagramm
01.06.2026
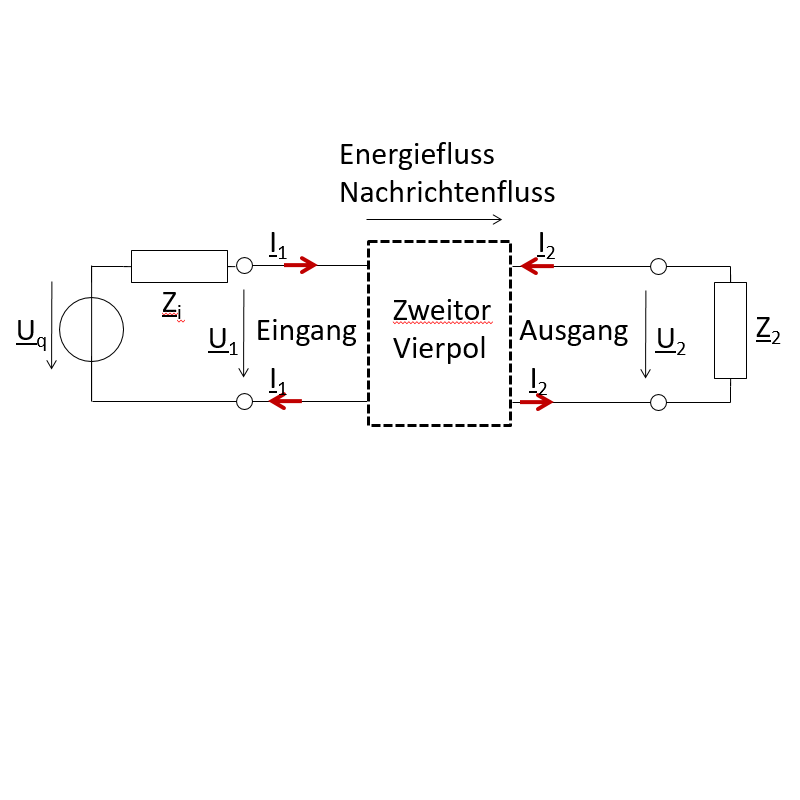
\( \underline{Z}_{ij} = \left. \frac{\underline{U}_{i}}{\underline{I}_{j}} \right\vert_{\underline{I}_{!j} = 0} \)
19. Vierpole
Eine Schaltung kann aus Vierpolen bestehen, die mit Matrizen beschrieben werden.\( \underline{Z}_{ij} = \left. \frac{\underline{U}_{i}}{\underline{I}_{j}} \right\vert_{\underline{I}_{!j} = 0} \)
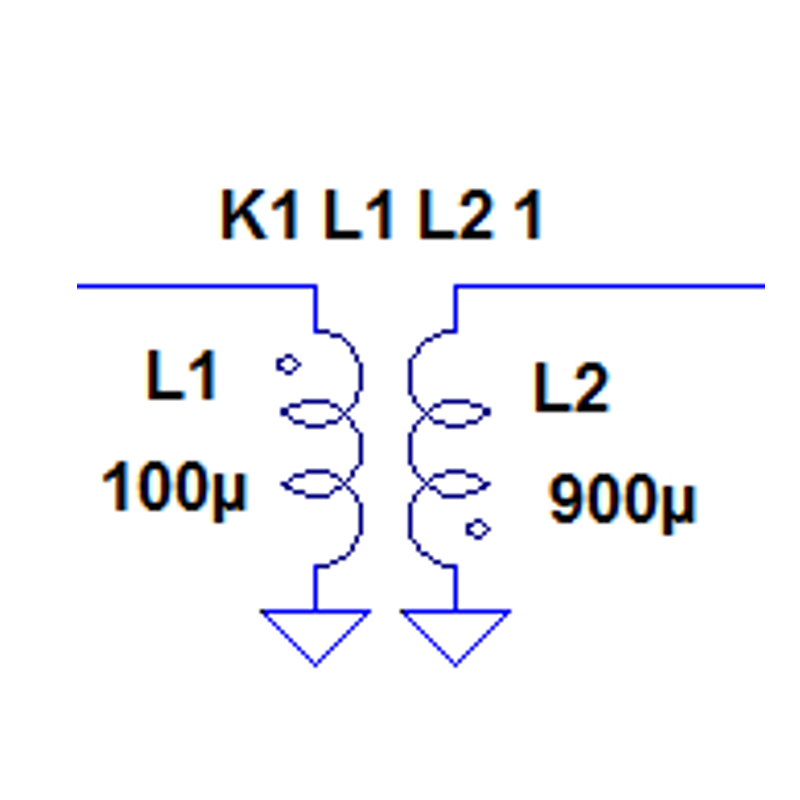
02.06.2026
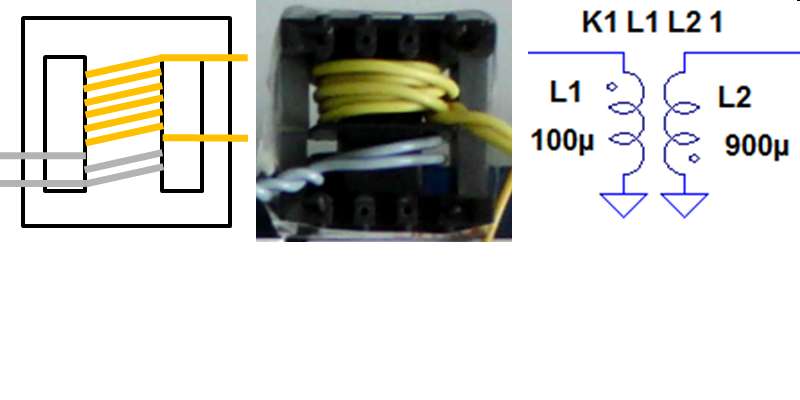
\( ü = \frac{U_1}{U_2} = \frac{N_1}{N_2} \) \( \underline{Z}_1 = ü^2 \underline{Z}_2 \)
\( M^2 = L_1 L_2 \) \( k = \frac{M}{\sqrt{L_1 L_2}} \)
3.06.2026 Übung 5a: Bodediagramm
23. Transformator
Übertragungsverhältnis ü und Widerstandstransformation:\( ü = \frac{U_1}{U_2} = \frac{N_1}{N_2} \) \( \underline{Z}_1 = ü^2 \underline{Z}_2 \)
\( M^2 = L_1 L_2 \) \( k = \frac{M}{\sqrt{L_1 L_2}} \)
3.06.2026 Übung 5a: Bodediagramm
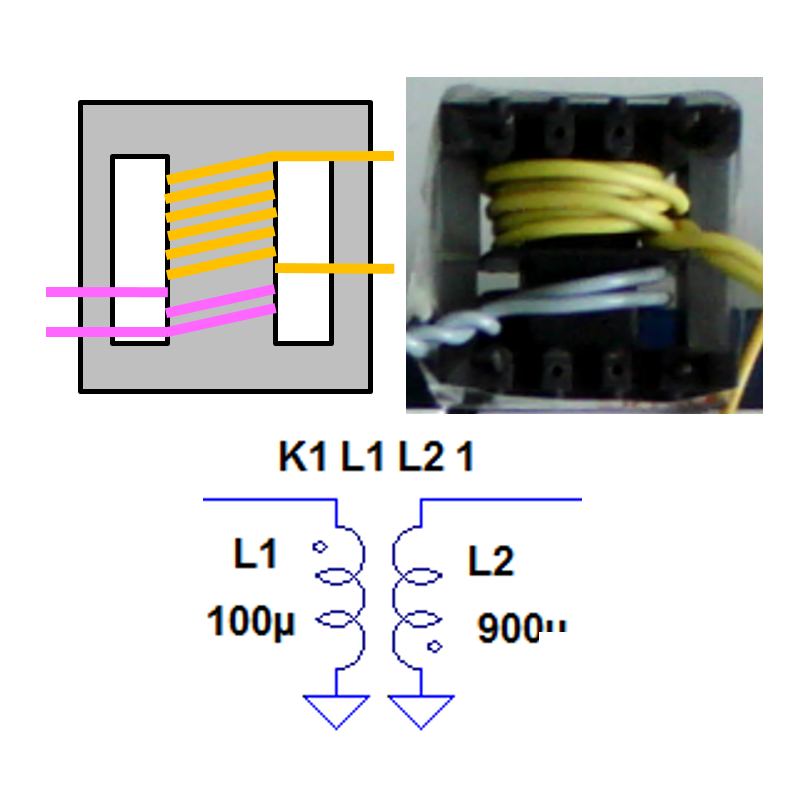
8.06.2026
Streuinduktivität
Eisenverluste
Ersatzschaltbilder
Leerlauf- und Kurzschlussmessung
Start Versuch 4: Transformator
24. Transformator
HauptinduktivitätStreuinduktivität
Eisenverluste
Ersatzschaltbilder
Leerlauf- und Kurzschlussmessung
Start Versuch 4: Transformator
9.06.2026
Ordnungszahl
10.06.2026 Übung 5b: Bodediagramm
Video:
Buch:
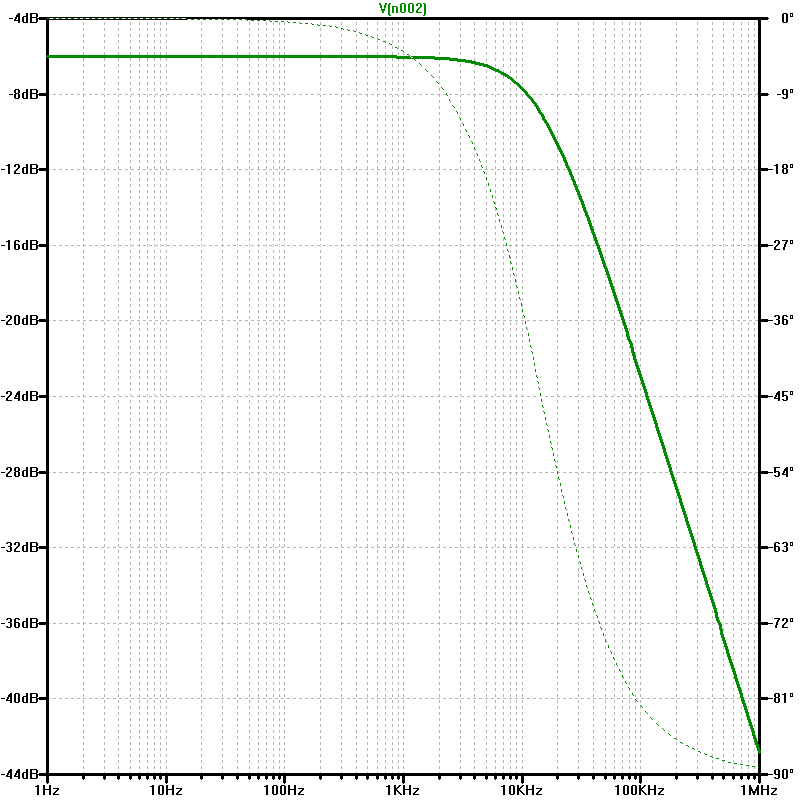
20. Filter
Grenzfrequenz oder EckfrequenzOrdnungszahl
10.06.2026 Übung 5b: Bodediagramm
Video:
Buch:
15.06.2026
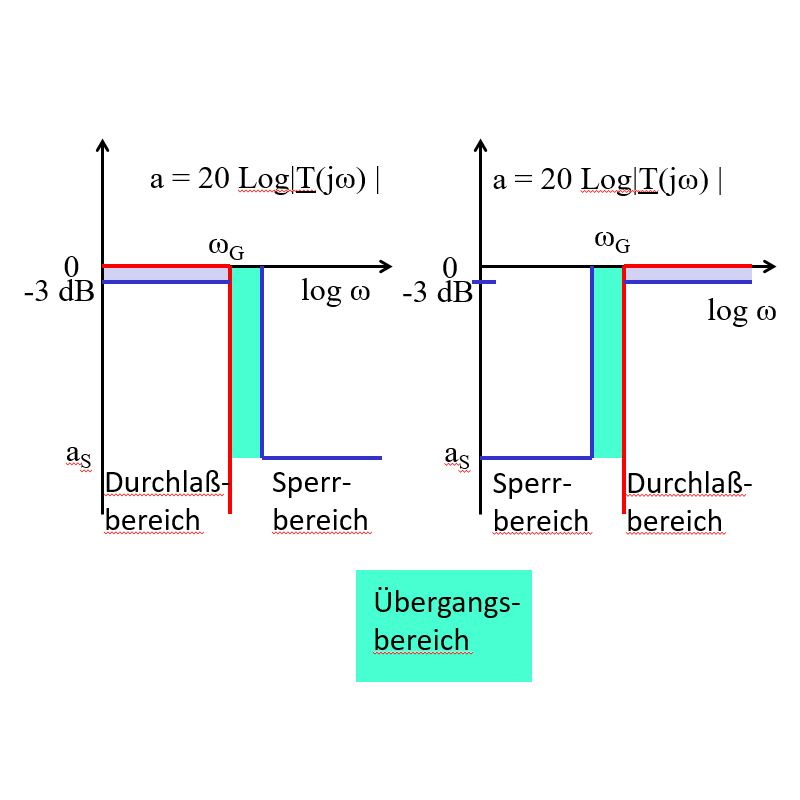
High pass, low pass
Video:
Buch:
21. Hochpass, Tiefpass
\( \underline{T}_H = \frac{j\omega}{j\omega - S_{P1}} \) \( \underline{T}_L = \frac{1}{j\omega - S_{P1}} \)High pass, low pass
Video:
Buch:
16.06.2026
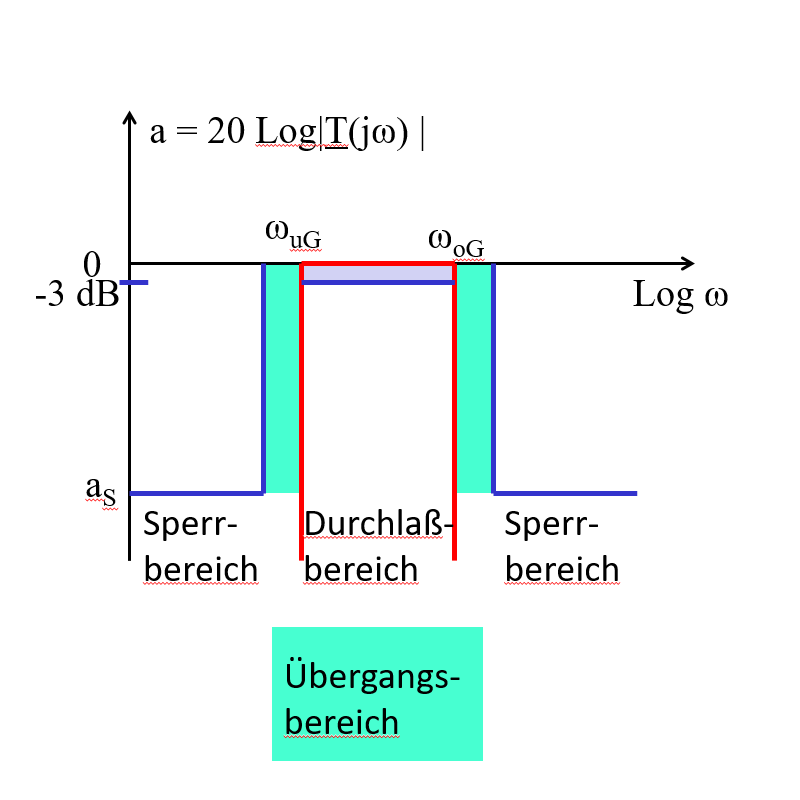
Bandsperre: 2 Nullstellen, 2 Pole
Güte
Video:
Buch:
22. Bandpass, Bandsperre
Bandpass: 1 Nullstelle, 2 PoleBandsperre: 2 Nullstellen, 2 Pole
Güte
Video:
Buch:
22.06.2026
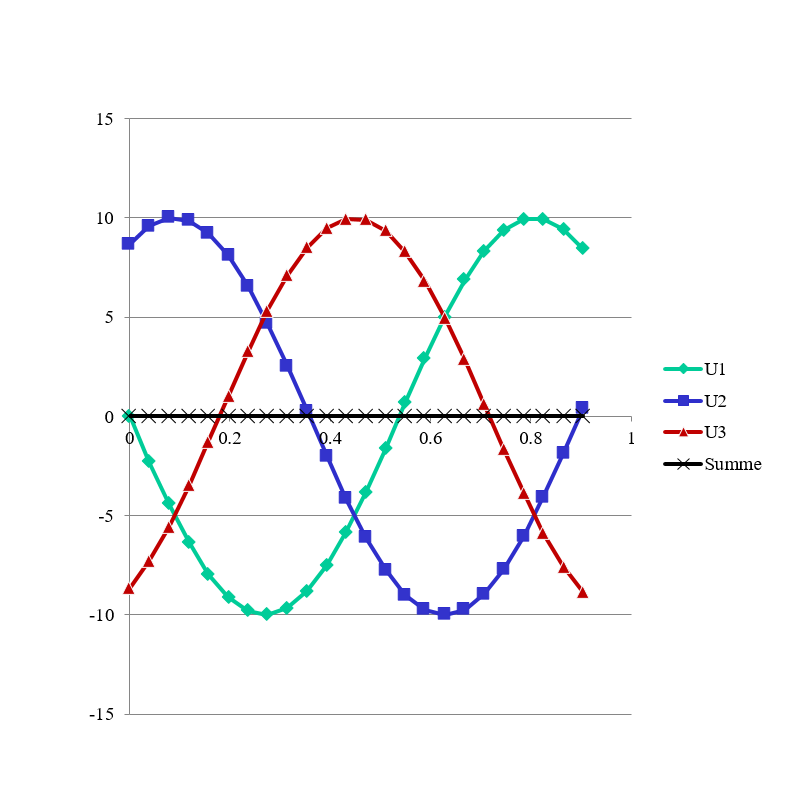
3 Phasen, dφ = 120°
Aussenleiterspannung: \( \underline{U}_{12} = \sqrt{3} U \underline{/30°} \)
Symmetrische Betrachtung
Drehstromgenerator, BLDC Motor
25.06.2025 Übung 6:
25. Drehstrom
Strangspannung (Sternspannung):3 Phasen, dφ = 120°
Aussenleiterspannung: \( \underline{U}_{12} = \sqrt{3} U \underline{/30°} \)
Symmetrische Betrachtung
Drehstromgenerator, BLDC Motor
25.06.2025 Übung 6:

6.7.2026
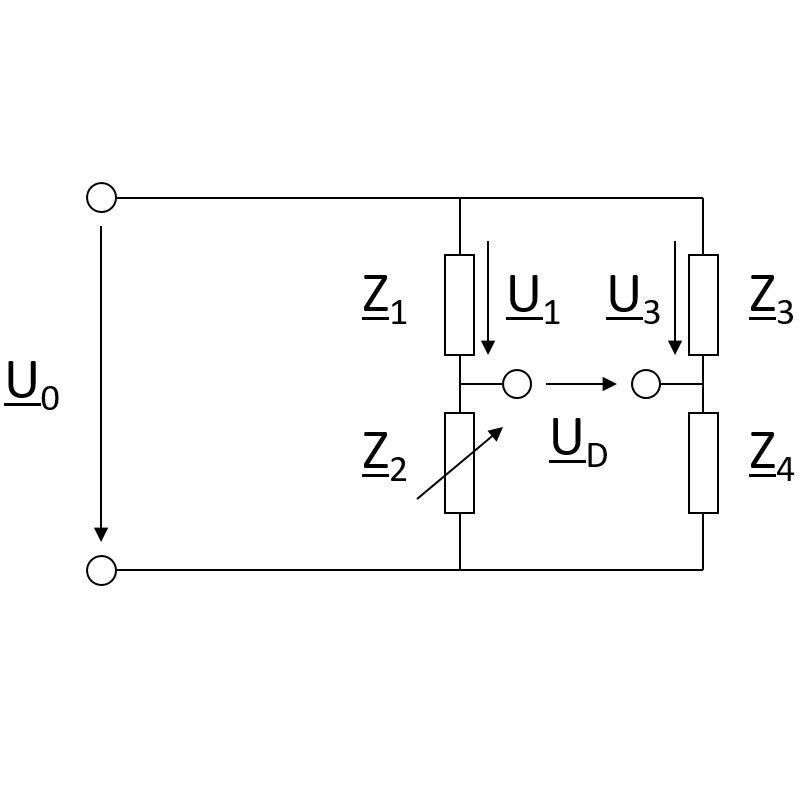
Quellenumwandlung, komplexe Leistung
Komplexer Widerstand, Resonanz, Spannungsüberhöhung, Ortskurve
Übertragungsfunktion, Filter
Bodediagramm, Filter
27. Testklausur
Wechselgrößen, Gleichwert, EffektivwertQuellenumwandlung, komplexe Leistung
Komplexer Widerstand, Resonanz, Spannungsüberhöhung, Ortskurve
Übertragungsfunktion, Filter
Bodediagramm, Filter
- Übung Grundlagen der Elektrotechnik 2
- Breadboard Demos und LTSPICE Simulations
Breadboard Demos
| Allzwecklabor ADALM2000, EEBench, Digilent Discovery | 02 Gleichwert und Effektivwert |
| Wechselspannungsmessung Dynamotaschenlampe | 01 Wechselgrößen |
| Lautsprecherweiche | 01 Wechselgrößen |
| U, I von R, L und C | 09 Kapazitäten und Induktivitäten |
| Schwingkreis Demo und Simulation | 12 Resonanz |
| Übertragungsfunktion Demo und Simulation | 18 Bode Diagram |
| Tiefpass Demo und Simulation | 20 Filter |
| Reihenschwingkreis Demo und Simulation | 22 Bandpass |
| Drehstrom am Drohnen BLDC Motor | 25 Drehstrom |
LTSPICE Simulations
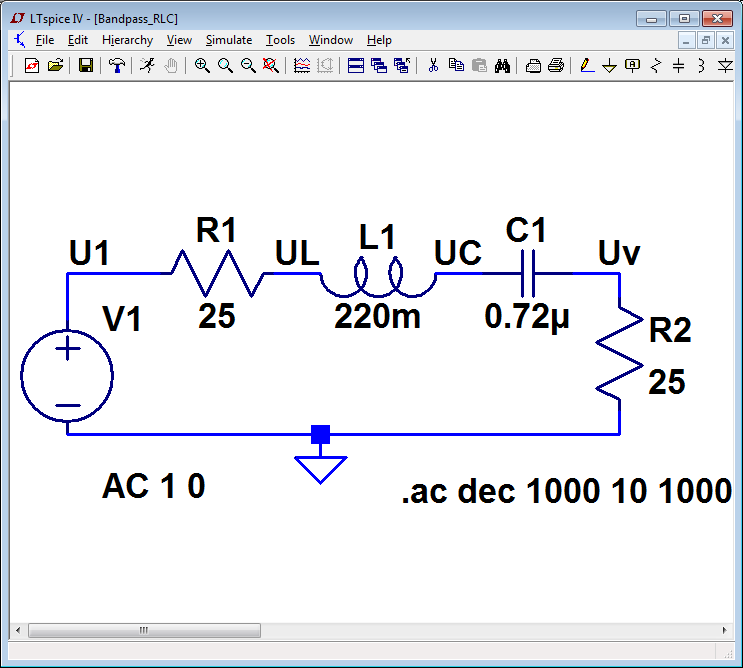
| Übertragungsfunktion (AC) einer RLCR Schaltung | 01 Wechselgrößen |
| Start LTSPICE mit einem Spannungsteiler | SPICE |
| Messung der Übertragungsfunktion einer Induktivität Lautsprecher |
SPICE |
| Ersatzquelle | 07 Ersatzquellen |
| Test Ersatzquelle | 07 Ersatzquellen |
| Test Ersatzquelle und Leistung | 07 Ersatzquellen |
| Test Ersatzquelle | 10 Reihenschaltung |
| Induktivitätsmessung Rechnung | 10 Reihenschaltung |
| Test komplexer Widerstand | 11 Parallelschaltung |
| Parallelschaltung | 11 Parallelschaltung |
| Parallelschaltung | 11 Parallelschaltung |
| Widerstandstransformation und Resonanz | 13 Schwingkreis |
| Mehrere Resonanzfrequenzen | 13 Schwingkreis |
| Ersatzquelle für mehrere Quellen | 14 Leistungsanpassung |
| Widerstandsfunktion | 15 Frequenzen |
| Ortskurve | 15 Frequenzen |
| Test Ortskurve | 16 Ortskurven |
| Li-Ion Akku Ortskurve | 16 Ortskurven |
| Bode Diagram LR | 18 Bode Diagram |
| Bode Diagram RRC | 18 Bode Diagram |
| Bode Diagram CRRL | 18 Bode Diagram |
| Hochpass | 21 Hochpass und Tiefpass |
| RC Verstärker | 21 Hochpass und Tiefpass |
| Elementarer Bandpass | 22 Bandpass |
| Bandsperre und Bandpass | 22 Bandpass |
| Bandsperre | 22 Bandpass |
| Tiefpass 2ter Ordnung | 22 Bandpass |
| Active Filter | 22 Bandpass |
| ESB Transformator | 23 Transformator |
| SPICE Transformator | 24 Transformator |
References
Grundlagen Elektrotechnik, Hochschule Karlsruhe