Interface Electronics

08 ADC architectures and sampling

Prof. Dr. Jörg Vollrath

Review and Overview

Sample/track and hold circuit

• kt/C noise
• Maximum resistance of RC low pass
• Clock jitter
• Switch charge injection and clock feedthrough

Track and hold sampling

Vout tracks Vin for half a cycle while the switch is closed. Then the switch is opened and Vout held constant. Ideally the switch is closed for a very short time and the input voltage instantly transfered to the output. It is a RC low pass circuit.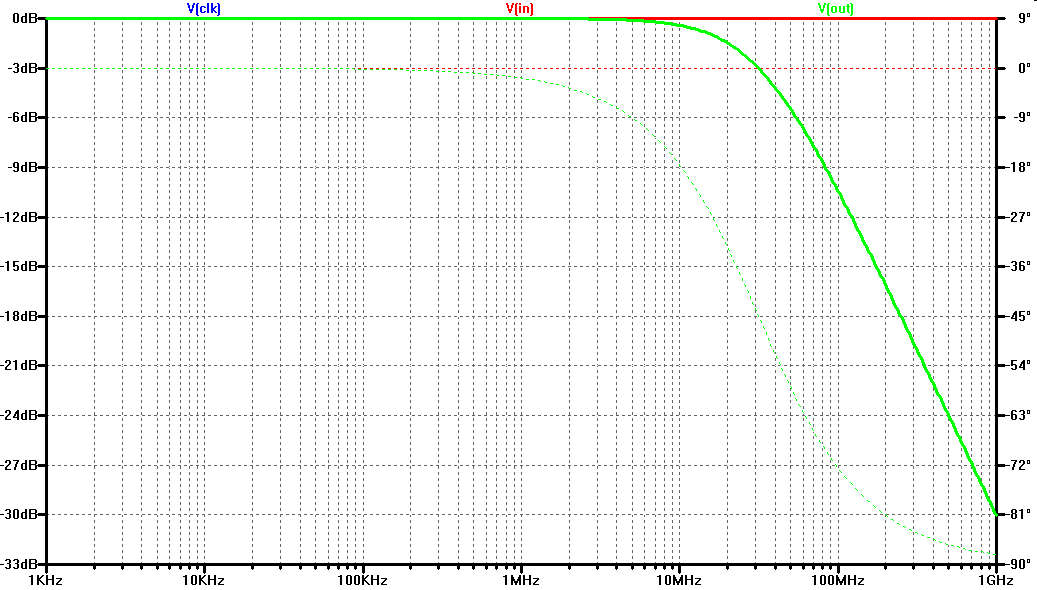

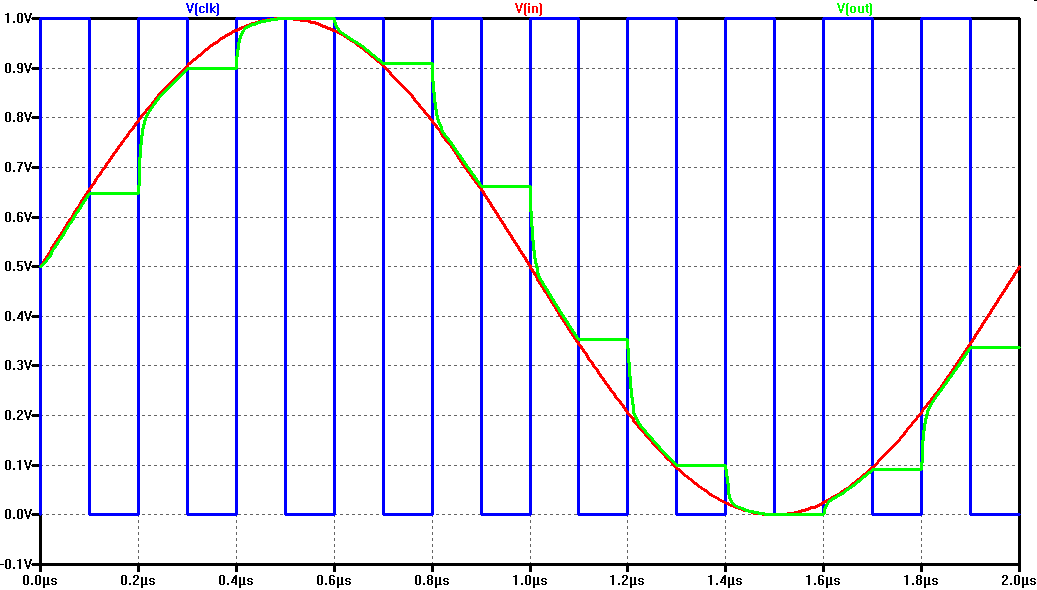
sample_hold_1.asc Nachgeladener SPICE Text Nachgeladener SPICE Text

Output voltage noise of a RC circuit

A resistor has a thermal noise density function of: \( V_{rR} \left( f \right) = \sqrt{4 \cdot k \cdot T \cdot R} \) T: absolute temperature k: Boltzman constant The rms output voltage noise can be calculated. The voltage divider gives the output voltage noise density: \( V_{out,noise} \left( f \right) = \sqrt{4 \cdot k \cdot T \cdot R} \frac{1}{1 + j \omega R C} \) The rms value can be calculated by integration over frequency as: \( V_{out,noise,rms} = \sqrt{ \int_0^{f_{3dB}\frac{\pi}{2}} V_{out,noise}^2 \left( f \right) df} \) \( V_{out,noise,rms} = \sqrt{ f_{3dB} \frac{\pi}{2} 4 k T R }\) \( V_{out,noise,rms} = \sqrt{ \frac{1}{2 \pi R C} \frac{\pi}{2} 4 k T R } = \sqrt{\frac{kT}{C}} \) Noise depends only on capacitance. For C = 1 pF and R = 10kΩ this gives 64 μV. As a rule of thumb peak to peak noise can be calculated with a factor of 6. 64 μ Vrms = 384 μ Vpp Reference: LTC signal chain seminar 2012, Noise

RC circuit: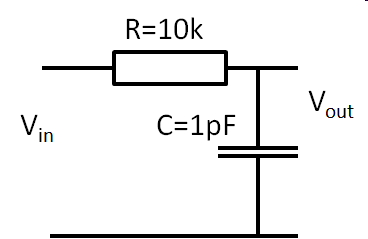 Equivalent noise circuit: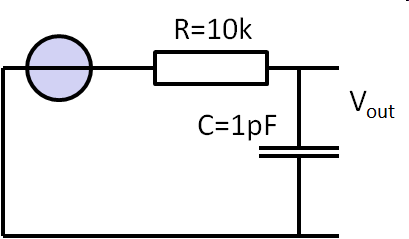

Sampling Network kt/C Noise

Quantization noise \( \approx \frac{LSB^2}{12} \) should be smaller than thermal noise: \( \frac{k_B \cdot T}{C} \) Giving: \( C \leq 12 \cdot k_B \cdot T \cdot LSB^2 \) \( C = 12 \cdot k_B \cdot T \cdot \frac{2^{2 \cdot N}}{V_{FS}^2} \)

Required C as a function of data converter resolution: N C(VFS= 3.3 V) C(VFS= 1 V) C(VFS= 0.5 V) Factor 0.1 1 4 Factor 8 0.3 fF 3 fF 12 fF 1/256 12 80 fF 0.8 pF 2.4 pF 1 16 20.6 pF 206 pF 824 pF 256 20 5.28 nF 52.8 nF 211.2 nF 65 k 24 1.35 μF 13.5 μF 54 μF 16 M

RC network time constant

C is determined by the thermal noise.
What maximum R can be tolerated for a RC network in a data converter?
The output voltage of a switched RC network is:
\( V_{out} = V_{in} \left( 1 - e^{- \frac{t}{\tau}}\right) \)
\( \tau = R \cdot C \)
The time t is limited by the sampling frequency \( f_s \). The maximum time is \( t = \frac{1}{2 \cdot f_S} \)
For a data converter the absolute difference between final value and current value has to be smaller than LSB.
\( | V_{out} - V_{in} | \lt LSB \)
\( V_{in} e^{- \frac{t}{\tau}} \lt LSB = \frac{V_{ref}}{2^{N}} \)
Worst case is \( V_{in} = V_{ref} \)

RC network time constant

\( e^{- \frac{t}{\tau}} \lt \frac{1}{2^{N}} \) \( \frac{t}{\tau} \gt ln\left(2^{N}\right) \) \( \frac{t}{R \cdot C} \gt N \cdot ln\left( 2 \right) \) The time t is limited by the sampling frequency \( f_s \). The maximum time is \( t = \frac{1}{2 \cdot f_S} \) \( R \lt \frac{1}{2 \cdot f_s \cdot C \cdot N \cdot ln\left( 2 \right)} \approx \frac{0.72}{N \cdot f_s \cdot C} \) The corner frequency of the RC circuit is: \( f_c = \frac{1}{2 \pi R \cdot C} = 0.22 \cdot N \cdot f_s \) A digital filter can correct this error.

Required R with VFS = 1 V as a function of data converter frequency: N R(fS = 1 MHz) R(fS = 100 MHz) R(fS = 1 GHz) Factor C * N 8 30 MΩ 300 kΩ 30 kΩ 256 * 4 12 75 kΩ 750 Ω 75 Ω 1 * 1 16 218 Ω 2.18 Ω 0.218 Ω 1/256 * 1/4 20 0.68 Ω 1/65k * 1/16

Transistor as a switch

Pass gate: NMOSFET VDD - Vth >> Vin otherwise Ron depends on Vin Transfer gate: NMOSFET parallel to PMOSFET Need CLK and /CLK with timing matching

Clock jitter

Effect of clock jitter on sampling of a sine signal: V(t) = A sin(ω t ) = A sin( 2 π fsig t ) A: Amplitude fsig: sine signal frequency Calculate the maximum difference of the voltage level with a jitter dt. The maximum slope of the signal is: V'(t) = A 2 π fsig sin( 2 π fsig t ) V'(t) = A 2 π fsig The voltage difference &Delta V = A 2 π fsig dt should be smaller than 0.5 LSB A 2 π fsig dt < 0.5 LSB The amplitude is: A = 2N - 1 LSB The maximum signal frequency is: \( f_{sig,max} = \frac{f_{sample}}{2} \) This gives for dt: \( dt < \frac{LSB}{2 \cdot A \cdot 2 \pi \cdot f_{sig,max}} \) \( dt < \frac{LSB}{2 \cdot 2^{N-1} LSB \cdot 2 \cdot \pi \cdot \frac{f_{sample}}{2}} \) \( dt < \frac{1}{ 2^{N} \cdot \pi \cdot f_{sample}} \)

Number of Bits N fsample td 12 1 GHz 0.0777 ps 12 10 MHz 7.77 ps 16 10 MHz 0.486 ps

Clock jitter

If the clock jitter is uncorrelated to the input signal it gives white noise.

Charge coupling and clock feed through

Overlap capacitance coupling Channel charge Source drain conduction Charge injection compensation switch (/CLK)

Sample and hold maximum performance

MOSFET switch: R and C are scaling Low leakage Small C, small R: checkerboard transistor