Processing math: 1%

Sigma delta ( $\Sigma \Delta$ ) analog to digital converter (ADC)

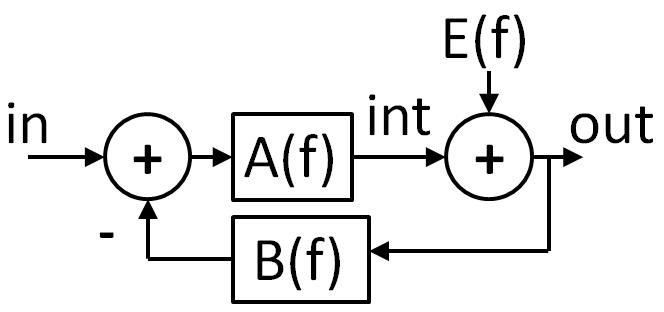
$\Sigma \Delta$ analog to digital converter (ADC) integrates (sigma) the difference (delta) between the input signal and an analog value generated by the current digital output code.
It is an oversampling ADC where the sample frequency

$f_{sampleIn}$ (clock frequency) is much higher than the bandwidth

$f_{bw}$ of interest.
The oversampling ratio OSR is defined as:

$OSR = \frac{f_{sampleIn}}{f_{sampleOut}}$

$f_{bw} = \frac{f_{sampleOut}}{2}$
A digital filter is used to downsample the digital output stream, increasing the number of bits and filtering out noise.

$\Sigma \Delta$ ADCs can be of different order, active using operational amplifiers or switched capacitor circuits and passive.
There are also cascaded (MASH)

$\Sigma \Delta$ ADCs to prevent instability.

Objectives:
1. Provide high level no cost JavaScript models in this web page.
2. Provide working LTSPICE transistor level models for simulation.
3. Provide simple low cost analog circuits with FPGA data processing for real experiments and measurement.

First Order $\Sigma \Delta$ ADC

A block diagram of a first order sigma delta ADC is shown here:

SigmaDelta.asc

Version 4
SHEET 1 1168 680
WIRE 0 128 -32 128
WIRE 112 128 96 128
WIRE 160 128 112 128
WIRE 256 128 240 128
WIRE 320 128 256 128
WIRE 464 144 432 144
WIRE 496 144 464 144
WIRE 48 176 48 160
WIRE 320 176 240 176
WIRE 48 304 48 176
WIRE 112 304 48 304
WIRE 192 304 112 304
WIRE 464 304 464 144
WIRE 464 304 320 304
FLAG -32 128 In
IOPIN -32 128 In
FLAG 496 144 Out
FLAG 112 128 S
FLAG 256 128 INT
FLAG 112 304 D
FLAG 240 176 CMP
SYMBOL sumR 48 128 R0
WINDOW 0 0 -40 Invisible 2
SYMATTR InstName X1
SYMBOL intRC 192 128 R0
SYMATTR InstName X2
SYMBOL Diffamp 384 144 R0
SYMATTR InstName X3
SYMBOL DAC1Bit 288 304 M0
SYMATTR InstName X4
TEXT 560 56 Left 2 !.global VDD CE RSTb CLK\nVCLK CLK 0 PULSE(0 1 0 0.1n 0.1n 100n 200n)\nVIN IN 0  SINE( 0.55 0.4 5798.33984375)\n*VIN IN 0 DC 0.45\nVDD VDD 0 DC 1\nVCMP CMP 0 DC 0.5\nVRST RSTb 0 DC 1\nVCE CE 0 DC 1\n.tran 0 3.2808m 4u\n* 100ns * 4 * 4096 (punkte fft) = 3.2768ms trans\n* 19 Perioden => 1/3.2768m*19 = 5798.33984375
TEXT -112 32 Left 2 !.include cmosedu_models.txt
TEXT -104 352 Left 2 !.options plotwinsize=0

On the left the difference of V(in) and V(D) is integrated and then compared with V(CMP). The comparator operates with the clock frequency and gives for each clock cycle a new value.
A simple passive first order sigma delta converter uses resistors and capacitances.

SigmaDeltaRC.asc

Version 4
SHEET 1 1168 680
WIRE 0 128 -32 128
WIRE 160 128 80 128
WIRE 272 128 160 128
WIRE 320 128 272 128
WIRE 464 144 432 144
WIRE 496 144 464 144
WIRE 80 160 80 128
WIRE 864 160 832 160
WIRE 976 160 944 160
WIRE 1040 160 976 160
WIRE 320 176 288 176
WIRE 160 208 160 192
WIRE 976 240 976 224
WIRE 80 304 80 240
WIRE 128 304 80 304
WIRE 352 304 128 304
WIRE 464 304 464 144
WIRE 464 304 416 304
FLAG -32 128 In
IOPIN -32 128 In
FLAG 496 144 Out
FLAG 272 128 INT
FLAG 128 304 ND
FLAG 288 176 CMP
FLAG 160 208 0
FLAG 976 240 0
FLAG 832 160 Out
FLAG 1040 160 out1
SYMBOL Diffamp 384 144 R0
SYMATTR InstName X3
SYMBOL cap 144 128 R0
SYMATTR InstName C1
SYMATTR Value 10p
SYMBOL res 64 144 R0
SYMATTR InstName R1
SYMATTR Value 200k
SYMBOL res 96 112 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 200k
SYMBOL INVx 384 304 M0
SYMATTR InstName X1
SYMBOL res 960 144 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R3
SYMATTR Value 200k
SYMBOL cap 960 160 R0
SYMATTR InstName C2
SYMATTR Value 10p
TEXT 560 48 Left 2 !.global VDD CE RSTb CLK\nVCLK CLK 0 PULSE(0 1 0 0.1n 0.1n 100n 200n)\nVIN IN 0  SINE( 0.55 0.4 5798.33984375)\n*VIN IN 0 DC 0.5\nVDD VDD 0 DC 1\nVCMP CMP 0 DC 0.5\nVRST RSTb 0 DC 1\nVCE CE 0 DC 1\n.tran 0 3.2808m 4u\n* 100ns * 4 * 4096 (punkte fft) = 3.2768ms trans\n* 19 Perioden => 1/3.2768m*19 = 5798.33984375
TEXT -72 64 Left 2 !.include cmosedu_models.txt
TEXT -88 328 Left 2 !.options plotwinsize=0

The voltage V(INT n+1) at clock cycle n+1 is:

$V_{int n+1} = V_{int n} + \frac{\delta t}{C} \left( \frac{ V_{not(Dout)} - V_{int n}}{R} + \frac{V_{in} - V_{int n}}{R} \right)$

$V_{int n+1} = V_{int n} + \frac{\delta t}{C \cdot R} \left( V_{not(Dout)} + V_{in} - 2 \cdot V_{int n} \right)$

$\delta t$ is the period of the clock.

$V_{Dout}$ in a real logic circuit is 0V or VDD.

A current is charging the capacitance.
An active sigma delta converter limits the swing of V(INT):

$V_{int n+1} = V_{int n} + \frac{\delta t}{C \cdot R} \left( V_{not(Dout)} + V_{in} - 2 \cdot V_{CMP} \right)$
A passive sigma delta converter can limit the swing of Vint with a small

$\frac{\delta t}{C \cdot R}$ These equations are implemented in JavaScript for simulation on this website.

The general signal and noise transfer function can be calculated:

$V_{out}(f) = \left( V_{in}(f) - B(f) V_{out}(f) \right) A(f) + E(f)$

$V_{out}(f) = V_{in}(f) A(f) - B(f) V_{out}(f) A(f) + E(f)$

$V_{out}(f) \left( 1 + B(f) A(f) \right) = V_{in}(f) A(f) + E(f)$

$V_{out}(f) = V_{in}(f) \frac{A(f)}{1 + B(f) A(f)} + E(f) \frac{1}{1 + B(f) A(f)}$
For a passive first order sigma delta modulator:

$\frac{v_{in} - v_{int}}{R} + \frac{-v_{out} - v_{int}}{R} = i_{int}$

$v_{in} - v_{int} - v_{out} - v_{int} = i_{int} R$

$v_{in} - v_{out} - 2 \cdot v_{int} = i_{int} R$

$v_{in} - v_{out} = i_{int} R + 2 \cdot v_{int}$

$i_{int} = v_{int} j \omega C$

$v_{int} = \frac{v_{in}-v_{out}}{j \omega C R + 2}$
Comparing this with the general signal and noise transfer function gives:

$B(f) = 1$

$A(f) = \frac{1}{j \omega C R + 2}$

$V_{out}(f) = V_{in} \frac{1}{j \omega C R + 3} + E(f) \frac{j \omega C R + 2}{j \omega C R + 3}$

$V_{out}(f) = \frac{V_{in}}{C R} \frac{1}{j \omega + \frac{3}{R C}} + E(f) \frac{j \omega + \frac{2}{R C}}{j \omega + \frac{3}{R C}}$

Bandwidth

$\frac{1}{\delta t} = f_{CLK}$ is the sampling frequency.
The low pass corner frequency f_3dB should be higher than

$\frac{f_{CLK}}{2 OSR} \lt f_{3dB}$ to prevent signal loss.

$f_{3dB} = \frac{1}{2 \dot \pi C R} \leq \frac{f_{CLK}}{2}$ to limit aliasing from higher frequencies. The low pass corner frequency is even smaller for oversampling.

$\frac{2 \pi}{2 OSR} \lt \frac{\delta t}{C \cdot R}$ .

To prevent gain error from the signal transfer function

$\frac{1}{| j \omega + 1 |} \gt (1 - 0.5 \frac{LSB}{V_{ref}} )$

$\frac{1}{| j \omega + 1 |} \gt (1 - \frac{1}{2^{N+1}} )$

$\frac{1}{\sqrt{ \omega^{2} + 1 }} \gt (1 - \frac{1}{2^{N+1}} )$

$\frac{1}{(1 - \frac{1}{2^{N+1}} )^2} \gt \omega^{2} + 1$

$\omega^{2} \lt \frac{1}{(1 - \frac{1}{2^{N+1}} )^2} - 1$

$\omega^{2} \lt \frac{1 - 1 + \frac{1}{2^N}- \frac{1}{2^{2N+2}}}{(1 - \frac{1}{2^{N+1}} )^2}$

$\omega^{2} \lt \frac{\frac{1}{2^N} \left( 1 - \frac{1}{2^{N+2}} \right) }{(1 - \frac{1}{2^{N+1}} )^2} \approx \frac{1}{2^N}$

$\omega \lt \frac{1}{2^\frac{N}{2}}$

Number of Bits	f_bw/f_gRC	OSR	f_gRC/f_bw	$\frac{\delta t}{C \cdot R} >$
1	0.88	1.5	1.1	3
4	0.25	6	3.9	2.1
8	0.065	38	16	1.33
12	0.015	240	64	0.835
16	0.0039	1521	256	0.53
20	0.00097	9660	1024	0.335
24	0.00024	61330	4096	0.21

$f_{gRC} > 2^\frac{N}{2} f_{bw} = \frac{2^\frac{N}{2}}{2 \cdot OSR} f_{sample}$ Otherwise there is a gain error for f_gRC.

$\frac{\delta t}{C \cdot R} = \frac{2 \pi f_{gRC}}{ f_{sample}} \gt \pi \frac{2^{\frac{N}{2}} }{OSR}$

Real circuit voltage limitations

The voltage V(INT) has to remain between V_DD and 0 V and centers around

$V(CMP) = \frac{VDD}{2}$ .

$0 \lt V_{CMP} + \frac{\delta t}{C \cdot R} \left( V_{not(Dout)} + V_{in} - 2 \cdot V_{CMP} \right) \lt VDD$

$0 \lt \frac{V_{DD}}{2} + \frac{\delta t}{C \cdot R} \left( V_{not(Dout)} + V_{in} - V_{DD} \right) \lt VDD$
mit

$V_{not(Dout)} + V_{in} = 0$ or

$2 \cdot VDD$

$\frac{\delta t}{C \cdot R} \lt \frac{1}{2}$

Summary R, C limitations

The internal voltage level has to stay between 0 V and V_DD.

$\frac{\delta t}{C \cdot R} = \frac{1}{f_{sample} \cdot C \cdot R} \lt \frac{1}{2}$
The input voltage swing for the comparator has to be above a certain minimum voltage

$\frac{V_{DD}}{gain}$ .

$v_{swing} = \frac{\delta t}{C \cdot R} V_{DD} > \frac{V_{DD}}{gain}$
The input low pass corner frequency has to be larger than the bandwidth.

$f_{bw} = \frac{1}{2 \pi C \cdot R} > \frac{f_{sample}}{2 OSR}$

$\frac{dt}{ C \cdot R} > \frac{2 \pi}{2 OSR}$

Example of first order sigma delta ADC

Compare voltage V(CMP) = 0.5 V
Type of sigma delta converter:
Factor

$0.1 \leq \frac{\delta t}{C \cdot R} \leq 0.5$ :
Minimum: 0.1 gives 0.1/2*VDD maximum step size of Vref = 1 V
Maximum: 0.5 makes sure Vint stays between 0 V and Vref = 1 V
Input voltage V(IN) [V] from 0..1:

Simulate sigma delta ADC

Time	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
V(INT)	0.5	0.46	0.62	0.58	0.54	0.5	0.66	0.62	0.58	0.54	0.5	0.66	0.62	0.58	0.54	0.5	0.66	0.62	0.58	0.54	0.5	0.66	0.62	0.58
V(OUT)	1	0	1	1	1	0	1	1	1	1	0	1	1	1	1	0	1	1	1	1	0	1	1	1
V(D)	0	1	0	0	0	1	0	0	0	0	1	0	0	0	0	1	0	0	0	0	1	0	0	0

The resistors and the capacitor form a lowpass.
The corner frequency of the low pass should be greater than the bandwidth of interest.

Bitstream

The following table shows typical code sequences and transition voltages Vt from one code sequence to the next for a passive 1st order sigma delta modulator with different factors

$\frac{\delta t}{C \cdot R} \leq 1$ of 0.2, 0.3, 0.1 affecting linearity.

Code	Vt(0.2) [V]	Vt(0.3) [V]	Vt(0.1) [V]
00000000...	0	0	0
00010001...	0.097	0.04	0.17
001001001..	0.183	0.11	0.27
01010101...	0.375	0.29	0.45
011011011..	0.7	0.75	0.68
01110111...	0.84	0.91	0.79
11111111...	1	1	1

A DC input creates low frequency tones which can be in the band of interest. To increase the number of bits while reducing the data rate a digital filter can be used.

Digital Filter

The simplest filter is an averaging filter. For sigma delta converters sinc filters and downsampling are used.

A ramp of the input voltage can be used to analyze the bit stream.
In this example a sinc1, sinc2 and sinc3 filter can be applied for several oversampling rates [6].
The JavaScript filter code can be found in the source code (function gen_simRamp) of this page.
The Histogramm should have an average value of 20.
Pulse duty cycle: %
Overshoot: %

Filter type: Output integer mapped to maximum SNR, ENOB 1st order sigma delta
Oversampling rate and (theoretical increase in number of bits for 1st order sigma delta):
Bit reduction:

Simulate ramp function and histogramm

A first order sigma delta converter gives a signal to noise ratio of:

$SNR = 6.02 \cdot N + 1.76 - 20 log \frac{2 \pi R C f_s}{\sqrt{12}} + 30 \log OSR$ (0, Baker, 6.17)
For

$R C f_s = 1$ this gives:

$SNR = 6.02 \cdot N + 1.76 - 5.17 + 30 \log OSR$
For

$R C f_s = 4.4, \frac{1}{R C f_s} = 0.22$ this gives:

$SNR = 6.02 \cdot N + 1.76 - 18.06 + 30 \log OSR$ (0, Baker, 6.18)
The increased resolution for oversampling is

$N_{inc} = \frac{ 30 log OSR - 5.17}{6.02}$
or

$OSR = 10^\frac{N_{inc} \cdot 6.02 + 5.17}{30}$

Doubling the oversampling rate OSR gives 1.48 more Bits:

$N_{inc} = \frac{ 30 log 2}{6.02} = 1.48$

To realize this increased resolution the order of the sinc filter has to be one more than the order of the delta sigma modulator. (6, TI)

A Sinc2 filter has the following schematic with 2 integrators and 2 differentiators:

The width W of the registers has to be adjusted accordingly to the gain: (6, TI)

$W = 1 + K \cdot log_2 OSR$
K is the order of the filter.

Example:
16 Bit resolution needs SNR = 97 dB and gives OSR = 1521.
The width of registers has to be

$W = 1 + 2 \cdot log_2 1521 \rightarrow 23$

VHDL code for 24 bit wide 2nd order SINC2 filter. [6, Texas Instruments]

VHDL code for 24 bit wide 2nd order SINC2 filter according to the block diagram above. (6, Texas Instruments)

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.std_logic_arith.all;
  
entity SINC2 is 
   generic(
      B: natural:=24 -- number of bits
   );
   port(RES, DIN, CLK, FSCLK, FBWCLK : in std_logic; 
        DOUT : out std_logic_vector(B downto 0)); 
end SINC2; 

architecture RTL of SINC2 is 
  signal DX : std_logic_vector(B downto 0); 
  signal DX1 : std_logic_vector(B-1 downto 0); 
  signal D0, D1, D2, D3 : std_logic_vector(B downto 0); 
  signal C0, C1, C2, C3 : std_logic_vector(B downto 0); 
begin 
   process(CLK, FSCLK, RES) 
   begin 
      if RES = '1' then 
         C1 <= (others => '0'); 
         C3 <= (others => '0'); 
      elsif CLK'event and CLK = '1' and FSCLK = '1' then 
         C1 <= C0; 
         C3 <= C2; 
      end if; 
   end process;
	DX1 <= (others => '0');
   DX <= DX1 & DIN;	
   C0 <= unsigned(DX) + unsigned(C1);
   C2 <= unsigned(C1) + unsigned(C3);
   
   process(RES, CLK, FBWCLK) 
   begin 
      if RES = '1' then 
         D0 <= (others => '0'); 
         D1 <= (others => '0'); 
         D3 <= (others => '0'); 
      elsif CLK'event and CLK = '1' and FBWCLK = '1' then 
         D0 <= C2; 
         D1 <= D0; 
         D3 <= D2; 
      end if; 
   end process; 
   D2 <= unsigned(D0) - unsigned(D1); 
   DOUT <= unsigned(D2) - unsigned(D3); 
 
end RTL;

Bitsequence filter example

FFT spectrum

A FFT spectrum of an ADC shows the noise transfer function and signal to noise ratio.
1) FFT of 1 bit stream: Signal and noise transfer function
2) FFT of stream after decimation
The filter needs some time to initialize.
Calculate total power of noise and signal and compare FFTs.

Effect of bleeding can be seen with number of periods non integer.

An droop compensating FIR Filter [ http://www.cypress.com/file/123171/download ] with a function:

$output(i) = \frac{-1}{K -2} input(i) + \frac{K}{K -2} input(i-1) + \frac{-1}{K -2} input(i-2)$
can be activated.
This filter function can be implemented in an FPGA employing shift, add, subtract (using 2s complement) and multiply. Fractions are normalized with the word width of the signal. K values can be taken from the link above.

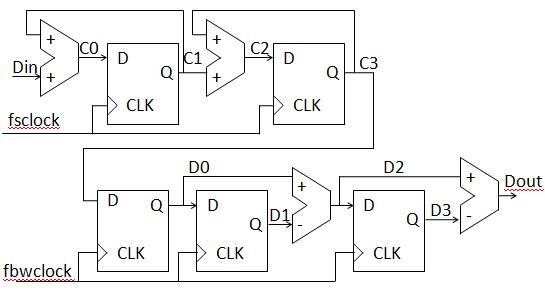
K values	up to Fs/16	up to Fs/8	up to Fs/4
sinc1	25.6573	24.65659	21.04096
sinc1 error +/- dB	0.00017	0.0027	0.045
sinc2	13.79721	13.20875	11.12903
sinc2 error +/- dB	0.0004	0.0064	0.104
sinc3	9.843906	9.393567	7.835116
sinc3 error +/- dB	0.0007	0.011	0.177

Using a non prime number (40) as number of periods shows non random quantization noise distribution.
Setting the number of periods to 0 shows the transfer function of the filter.
Setting the number of periods to a negative value between -1 and 0 generates a DC value. Example: -0.615

FFT curve1: FFT curve2:
Number of periods (integer prime number): Possible values: 0, 3, 4.5, 7, 40, 43, 509, 1009, 1523, 1999
Oversampling rate:
Number of FFT points:
Bit width of filter:
Filter coefficient K:

Windowing for curve 1:

Simulate sine function into sigma delta ADC

Sinc1 Signal: -9.03 dB, Noise peak: -43 dB Total Noise: -26 dB Signal to Noise: 17dB
1 Bit Signal: -8.91 dB, Noise peak: -28 dB Total Noise: -9 dB Signal to Noise: 0dB
Duration of calculation: 21 ms = 0 min
Duration1 of calculation: 4 ms = 0 min

Curve 1					Curve 2
Frequency	Signal magnitude dB	Total noise magnitude dB	SNR dB	ENOB	Frequency	Signal magnitude dB	Total noise magnitude dB	SNR dB	ENOB
0	-6.02	-11.96	5.94	0.69	0	-6.11	-9.03	2.92	0.19
3	-12.04	-29.25	17.21	2.57	3	-11.92	-12.17	0.25	-0.25
366	-46.11	-29.34	-16.77	-3.08	110	-30.53	-12.23	-18.3	-3.33
376	-46.87	-29.41	-17.46	-3.19	500	-30.98	-12.29	-18.69	-3.4
342	-47.19	-29.49	-17.7	-3.23	366	-31.3	-12.34	-18.96	-3.44
496	-47.26	-29.56	-17.7	-3.23	424	-31.4	-12.4	-19	-3.45
418	-47.47	-29.63	-17.84	-3.26	490	-31.94	-12.44	-19.5	-3.53
454	-47.77	-29.7	-18.07	-3.29	298	-32.09	-12.49	-19.6	-3.55
350	-47.93	-29.76	-18.17	-3.31	187	-32.1	-12.54	-19.56	-3.54
453	-48.03	-29.83	-18.2	-3.32	94	-32.36	-12.59	-19.77	-3.58
380	-48.15	-29.89	-18.26	-3.33	230	-32.63	-12.63	-20	-3.61

Droop filter function

To investigate the transfer function levels at some frequencies are shown here in tabular form.
Select Number of periods: 0 to see the transfer function.
The transfer functio with FIR will show less droop at higher frequencies.

For the first and 2nd curve the level at different points are calculated

Level (frequency)	Magnitude	Bits curve 1	Magnitude 2	Bits curve 2
A(2) [dB]	-93.677		-37.572
A(32) [dB]	-63.897	-4.899	-29.871	-0.513
A(64) [dB]	-74.037	-3.103	-44.781	0.826
A(128) [dB]	-54.905	-6.423	-29.769	-0.541
A(256) [dB]	-53.555	-6.65	-32.24	0.239
A(511) [dB]	-49.314	-7.36	-35.242	1.7

Results:

1st order passive sigma delta modulator FFT results.
SNR = 6.02 NBit dB + 1.76 dB + 30 · log(OSR)
Signal to noise ratio (SNR) in dB

OSR	30 log(OSR) dB	SINC1	SINC2	SINC3	Number of points FFT, register width W
4	18	11	17	18	Valid, FFT 1024, 16 Bit
8	27	17	25	27	Valid, FFT 1024, 16 Bit
32	45	29	40	42	Valid, FFT 1024, 16 Bit
256	72	47	63	64	Valid, FFT 1024, 30 Bit
512	81	53	71	72	Valid, FFT 1024, 30 Bit
2048	99	65	86	87	Valid, FFT 1024, 40 Bit

FFT 256k, Bit width 30, oversampling 32, Duration 2 min
FFT 256k, Bit width 30, oversampling 512, Duration 7 min
FFT 1M, Bit width 30, oversampling 512, Duration 27 min

An OSR = 256 can give 10 Bit.
An FPGA running at 100 MHz can sample 44kHz audio and gives an OSR = 2048 and 14 Bit with a 1st order sigma delta modulator and a sinc2 filter.

Table with required register width W = 1 + K log2 OSR for different OSRs and sinc filters.

OSR	SINC1	SINC2	SINC3
4	3	5	7
8	4	7	10
32	6	11	16
256	9	17	25
512	10	19	28
2048	12	23	34
16k	15	29	43

Summary

The influence of the R and C of a first order sigma delta converter for correct functionality to avoid saturation at the input of the integrator can be studied.

Digital sinc filters are presented in VHDL code and as simulation.
A ramp test giving a histogram for these filters can be generated showing big errors.
Typical output bit sequences are presented before and after filtering and decimation.
Spectral test varying filter width, FFT points and filters can be studied.
Usage of non integer number of periods show bleeding in the FFT.
Limitations of small filter width and influence of filter on the transfer characteristics can be seen.
Droop of the sinc filter has to be compensated by an additional FIR filter or is limiting the usable bandwidth.

An FPGA running at 100 MHz can sample 44kHz audio and gives an OSR = 2048 and 14 Bit with a 1st order sigma delta modulator and a sinc2 filter.
Doubling the oversampling rate OSR can give 1.48 more Bits.

Open Question:
Changing dt/R/C shows no change in SNR in the simulation.

References

[0] CMOS Mixed-Signal Circuit Design, R. Jacob Baker "http://cmosedu.com/cmos2/book2.htm"
[1] Analog Devices Sigma Delta converter simulation "http://www.analog.com/en/design-center/interactive-design-tools/sigma-delta-adc-tutorial.html"
[2] Demystifying Delta-Sigma ADCs "https://www.maximintegrated.com/en/app-notes/index.mvp/id/1870"
[3] Wikipedia Delta-sigma modulation https://en.wikipedia.org/wiki/Delta-sigma_modulation
[4] Texas Instruments http://www.ti.com/lit/an/slyt423/slyt423.pdf
[5] Nuts and Bolts of the Delta-Sigma Converter, Texas Instruments, https://www.youtube.com/watch?v=oVti3b4rqQA
[6] Combining the ADS1202 with an FPGA Digital Filter for Current Measurement in Motor Control Applications, Texas Instruments, VHDL code
[7] Wikipedia Window function
Window function - Wikipedia

Version 4
SymbolType BLOCK
LINE Normal -32 0 -48 0
LINE Normal 16 0 -15 0
LINE Normal 0 16 0 -16
LINE Normal 32 0 48 0
LINE Normal 0 32 0 48
LINE Normal -32 0 -39 -9
LINE Normal -39 8 -32 0
LINE Normal 0 32 -8 40
LINE Normal 7 39 0 32
LINE Normal -16 40 -48 40
LINE Normal -56 -16 -56 -48
LINE Normal -38 -32 -72 -32
CIRCLE Normal 32 32 -32 -32
WINDOW 0 0 -40 Bottom 2
PIN 0 48 NONE 8
PINATTR PinName Inm
PINATTR SpiceOrder 1
PIN -48 0 NONE 8
PINATTR PinName Inp
PINATTR SpiceOrder 2
PIN 48 0 NONE 8
PINATTR PinName Out
PINATTR SpiceOrder 3

Version 4
SymbolType BLOCK
LINE Normal -32 47 -32 -48
LINE Normal 48 0 -32 47
LINE Normal -32 -48 48 0
TEXT -16 -2 Left 2 Int
WINDOW 0 0 -49 Bottom 2
PIN -32 0 NONE 8
PINATTR PinName in
PINATTR SpiceOrder 1
PIN 48 0 NONE 8
PINATTR PinName out
PINATTR SpiceOrder 2

Version 4
SymbolType BLOCK
LINE Normal -25 -16 -57 -16
LINE Normal -41 -1 -41 -33
LINE Normal -26 32 -58 32
LINE Normal -64 -64 48 0
LINE Normal -64 64 -64 -64
LINE Normal 48 0 -64 64
WINDOW 0 32 -40 Bottom 2
PIN -64 32 NONE 8
PINATTR PinName M
PINATTR SpiceOrder 1
PIN -64 -16 NONE 8
PINATTR PinName P
PINATTR SpiceOrder 2
PIN 48 0 NONE 8
PINATTR PinName Y
PINATTR SpiceOrder 3

Version 4
SymbolType BLOCK
LINE Normal -32 48 -32 -49
LINE Normal 66 48 -32 48
LINE Normal 97 0 66 48
LINE Normal 64 -48 97 0
LINE Normal -32 -48 64 -48
TEXT -2 1 Left 2 DAC
WINDOW 0 0 -80 Bottom 2
PIN -32 0 NONE 8
PINATTR PinName D
PINATTR SpiceOrder 1
PIN 96 0 NONE 8
PINATTR PinName Q
PINATTR SpiceOrder 2

Version 4
SymbolType BLOCK
LINE Normal -31 -15 9 1
LINE Normal -31 17 9 1
LINE Normal -31 17 -31 -15
LINE Normal 25 1 33 1
CIRCLE Normal 25 9 9 -7
WINDOW 0 0 -24 Bottom 0
PIN -32 0 NONE 8
PINATTR PinName A
PINATTR SpiceOrder 1
PIN 32 0 NONE 8
PINATTR PinName Y
PINATTR SpiceOrder 2

Code	Average 1st order Integrator	2nd order Integrator	2nd order Differentiator Decimation 4	3rd order Integrator
0000 0000	0,0,0,0 0,0,0,0	0,0,0,0, 0,0,0,0	0, 0	0,0,0,0, 0,0,0,0
0001 0001	0,0,0,1 1,1,1,2	0,0,0,1, 2,3,4,6	1, 5	0,0,0,1, 3,6,10,16
0010 0010	0,0,1,1 1,1,2,2	0,0,1,2, 3,4,6,8	2, 4	0,0,1,3, 6,10,12,20
0011 0011	0,0,1,2 2,2,3,4	0,0,1,3, 5,7,10,14	3, 11	0,0,1,4, 9,16,26,40
0100 0100	0,1,1,1 1,2,2,2	0,1,2,3, 4,6,8,10	3, 7	0,1,3,6, 10,16,24,34
0101 0101	0,1,1,2 2,3,3,4	0,1,2,4, 6,9,12,16	4, 12	0,1,3,7, 13,22,34,50
0110 0110	0,1,2,2 2,3,4,4	0,1,3,5, 7,10,14,18	5, 13	0,1,4,9, 16,26,40,58
0111 0111	0,1,2,3 3,4,5,6	0,1,3,6, 9,13,18,24	6, 18	0,1,4,10, 19,32,50,74
1000 1000	1,1,1,1 2,2,2,2	1,2,3,4, 6,8,10,12	4, 8	1,3,6,10, 16,24,34,46
1001 1001	1,1,1,2 3,3,3,4	1,2,3,5, 8,11,14,18	5, 13	1,3,6,11, 19,30,44,62
1010 1010	1,1,2,2 3,3,4,4	1,2,4,6, 9,12,16,20	6, 14	1,3,7,13, 22,34,50,70
1011 1011	1,1,2,3 4,4,5,6	1,2,4,7, 11,15,20,26	7, 19	1,3,7,14, 25,40,60,86
1100 1100	1,2,2,2 3,4,4,4	1,3,5,7, 10,14,18,22	7, 15	1,4,9,16, 26,40,58,80
1101 1101	1,2,2,3 4,5,5,6	1,3,5,8, 12,17,22,28	8, 20	1,4,9,17, 29,46,68,96
1110 1110	1,2,3,3 4,5,6,6	1,3,6,9, 13,18,24,30	9, 21	1,4,10,19, 32,50,74,104
1111 1111	1,2,3,4, 5,6,7,8	1,3,6,10, 15,21,28,36	10, 26	1,4,10,20, 35,56,84,120

Sigma delta ( \Sigma \Delta \Sigma \Delta ) analog to digital converter (ADC)

First Order \Sigma \Delta \Sigma \Delta ADC