Test for 4 Bit ADC and DAC
|
A 4 Bit ADC and DAC test can be simulated in LTSPICE. The files were downloaded and LTSpice simulation was started. The output file size can be limited by using the .save dialog option. A voltage source was added with a ramp from 0 V to 1 V with a rise time of 655µs. The picture shows a ramp input voltage and the DAC ramp output voltage over time 16 steps can be seen. With a measurement statement the voltage level were extracted.
The following code has been used for measurement, .Measure TRAN V0000 FINDV(Vout) AT= 20u .Measure TRAN V0001 FINDV(Vout) AT= 60u .Measure TRAN V0002 FINDV(Vout) AT= 100u .Measure TRAN V0003 FINDV(Vout) AT= 140u .Measure TRAN V0004 FINDV(Vout) AT= 180u .Measure TRAN V0005 FINDV(Vout) AT= 220u .Measure TRAN V0006 FINDV(Vout) AT= 260u .Measure TRAN V0007 FINDV(Vout) AT= 300u .Measure TRAN V0008 FINDV(Vout) AT= 340u .Measure TRAN V0009 FINDV(Vout) AT= 380u .Measure TRAN V0010 FINDV(Vout) AT= 420u .Measure TRAN V0011 FINDV(Vout) AT= 460u .Measure TRAN V0012 FINDV(Vout) AT= 500u .Measure TRAN V0013 FINDV(Vout) AT= 540u .Measure TRAN V0014 FINDV(Vout) AT= 580u .Measure TRAN V0015 FINDV(Vout) AT= 620u No error in the voltage level can be seen.It is an ideal ADC and DAC.  |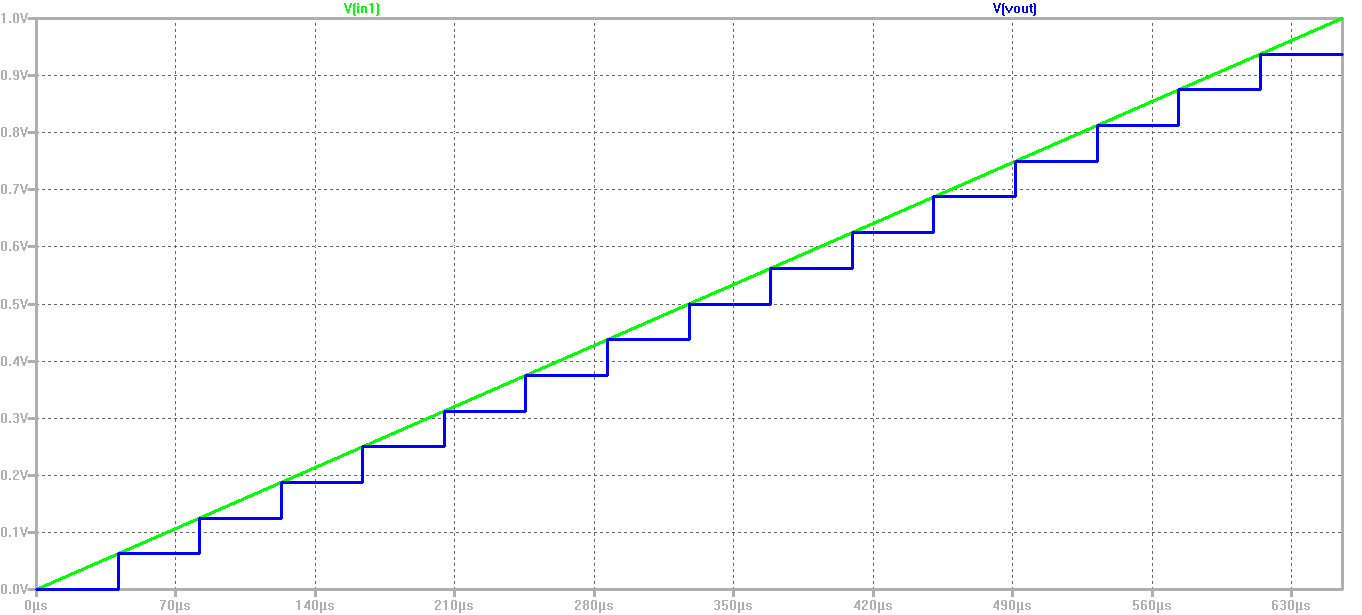
LTSPICE schematics
|
Here it is a schematic of 3 bit DAC after simulating this model we have calculated DNL and INL. From DNL and INL we know how a DAC will behave.
For this calculation we need LSB, In our case LSB is 0.5 LSB= (V(111)-V(000))/(2^3)-1 To get the DNL I have used this formula given below, DNL(n)=(V(n)-V(n-1)-LSB)/LSB As we know LSB is calculated using the initial and the end code, so the sum of all DNL should be zero. The formula for the INL calculation is, INL(n)=(Vout(n)-Videal(n))/LSB Since the INL is calculated using the first and last code: INL(000) = 0; INL(111) = 0; The Output graph and result of calculation is given below:   |