Elektronik 302 HalbleiterProf. Dr. Jörg Vollrath01 SPICE Schaltungssimulation |
Video der 2. Vorlesung
|
Länge: 01:06:27 |
0:0:0 Tiefpass, LTSPICE 0:1:5 LTSPICE verifizieren einer Rechnung 0:2:50 Knotennamen Ua, Ue 0:3:25 Spannungsquelle platzieren 0:5:35 Simulation Spannungen und Ströme .op 0:7:15 Erwartungen an das Ergebnis 0:7:45 .dc DC sweep Spannungsvariation 0:8:15 Netzliste 0:9:5 Ergebnisgrafik, Kurven hinzufügen 0:10:20 Kontextsensitive Menues 0:10:44 Zeitsimulation .tran Transientenanalyse 0:12:36 Einschalten, Einschwingen 0:13:20 Einschalten, stationärer Zustand, Ausschalten, Aus 0:14:35 Cursorablesung 0:16:10 Add Trace mit einer mathematischer Funktion 0:17:24 Niedrigere Frequenz und Phasenverschiebung 0:18:45 Übertragungsfunktion AC-Simulation 0:20:27 Grafische Darstellung mit Maß und Phase 0:21:25 dB Umrechnung, Betrag, 20 log |UA/UE| 0:24:8 Grosse Werte omega -20 dB pro Dekade (Faktor 10 in der Frequenz) 0:25:43 Analyse der grafischen Darstellung Betrag und Phase 0:27:53 SPICE Folien 0:28:53 SPICE Programme 0:30:13 Herunterladen der Schaltungen 0:31:51 Spannungsquellenverlauf über eine Textdatei 0:32:48 Messwerte (Zeit, Amplitude, Spannungswert) in LTSPICE extrahieren .MEAS 0:35:3 Warum simulieren wir und rechnen nicht nur? 0:36:48 Halbleiter und Mitschrift 0:36:48 Lineare und nichtlineare Bauelemente 0:38:17 Diodenkennlinie 0:39:2 Messschaltung, Simulation 0:40:0 Idee und Schaltung 0:40:47 Das Steckbrett 0:41:17 Schaltplan und Schaltungsaufbau 0:44:7 Beispielberechnung Widerstand eines Kupferdrahtes 0:46:37 Gruppenarbeit Start 0:46:37 Leitfähigkeit 0:48:32 Einheiten 0:49:2 Abschätzung ohne Taschenrechner im Kopf 0:50:0 Ergebnisdiskussion 0:51:52 Werkstofftabelle 0:53:39 Halbleiter im Periodensystem 0:55:2 Bandlücke 0:57:22 Eigenleitungsdichte 0:59:12 Siliziumatome im Halbleiter 1:1:37 Spezifische elektrische Leitfähigkeit eines Halbleiters 1:2:47 Eigenleitungsdichte Formel 1:4:22 Massenwirkungsgesetz 1:4:52 Grafische Darstellung der Eigenleitungsdichte |
Rückblick
- Organisation
- LTSPICE
- Heruntergeladen?
- Im Rechnerraum ausprobiert?
- Arbeitspunkt
- Zeitliche Simulation
- Bauteile
- Spannungsquelle
- Masse
- Widerstand
- Kapazität
- Buch oder Skript
Was haben Sie sich das letzte Mal notiert?
Was war wichtig?
Was sind die 3 wichtigen Einstellungen beim Oszilloskop?
Was ist eine Übertragungsfunktion?
Was sind aktive und passive Bauelemente?
Was war wichtig?
Was sind die 3 wichtigen Einstellungen beim Oszilloskop?
Was ist eine Übertragungsfunktion?
Was sind aktive und passive Bauelemente?
Motivation Halbleiter und Diode
|
|
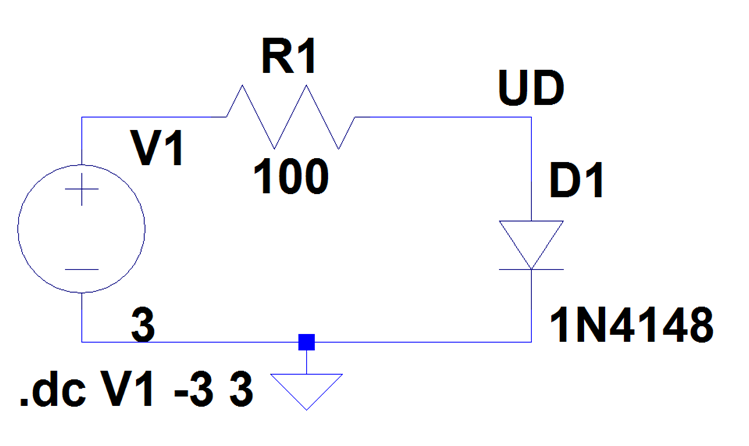
Warum gibt es lineare und nichtlineare Bauelemente?
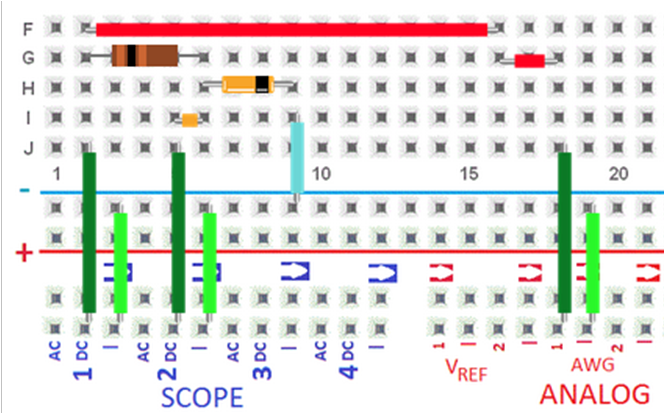
Hier wird eine Messung mit dem Electronic Explorer gezeigt, wie sie auch im Praktikum durchgeführt wird.
Eine Anleitung zur Bedienung des Electronic Explorers finden Sie hier .
Welches sind die 3 wichtigsten Einstellmöglichkeiten des Oszilloskops?
x-Achse: Zeit, time; y-Achse: range, offset; Trigger: Kanal, Flanke, Pegel, channel, edge, level
Der Signalgenerator mit einer Dreiecksspannung wird als Quelle verwendet.
Mit einem Widerstand wird der Strom gemesssen.
Am Oszilloskop wird zur Bestimmung des Stromes die Mathematikfunktion M1 = (C1 - C2) / R aktiviert.
Mit der x-y Darstellung kann man die statische Kennlinie I(U) = M1(C2) darstellen.
Man sieht die Nichtlinearität der Kennlinie.
Hier wird eine Messung mit dem Electronic Explorer gezeigt, wie sie auch im Praktikum durchgeführt wird.
Eine Anleitung zur Bedienung des Electronic Explorers finden Sie hier .
Welches sind die 3 wichtigsten Einstellmöglichkeiten des Oszilloskops?
x-Achse: Zeit, time; y-Achse: range, offset; Trigger: Kanal, Flanke, Pegel, channel, edge, level
Der Signalgenerator mit einer Dreiecksspannung wird als Quelle verwendet.
Mit einem Widerstand wird der Strom gemesssen.
Am Oszilloskop wird zur Bestimmung des Stromes die Mathematikfunktion M1 = (C1 - C2) / R aktiviert.
Mit der x-y Darstellung kann man die statische Kennlinie I(U) = M1(C2) darstellen.
Man sieht die Nichtlinearität der Kennlinie.
Ziele
- Welche elektrische Werkstoffe gibt es?
- spezifischen Widerstand
- elektrische Leitfähigkeit
- Welche Werkstoffe werden in elektrischen Geräten verwendet?
- Was ist der Unterschied zwischen Leitern, Halbleitern und Isolatoren?
- Wie viele Atome und freie Ladungsträger sind in Leitern, Halbleitern und Isolatoren vorhanden?
- Wie berechnet man den spezifischen Widerstand und die elektrische Leitfähigkeit?
Elektronische Schaltungstechnik, Reinhold: Kapitel 1, S. 13-21
Microelectronic, Jaeger: Chapter 2, page: 42-70
Elektrischer Leiter, Halbleiter, Isolatoren
(Conductor, Semiconductor, Isolator)
Spezifischer Widerstand und Leitfähigkeit
\( \left[\kappa\right]= \frac{1}{\Omega m} = \frac{S}{m} \frac{A}{V m} \) |
|
Werkstoffe (Wikipedia)
| Stoff | Symbol | Dichte [g/cm3] | Elektrische Leitfähigkeit A/(Vm) | Kategorie |
| Gold | Au | 19.32 | \( 45.5·10^6 \) | Leiter \( \rho \lt 10^{-3}\Omega cm \) |
| Silber | Ag | 10.49 | \( 61.35·10^6 \) | |
| Platin | Pt | 21.54 | \( 9.43·10^6 \) | |
| Aluminium | AL | 2.7 | \( 37.7·10^6 \) | |
| Kupfer | Cu | 8.92 | \( 59.1·10^6 \) | |
| Stahl | Fe | 7.874 | \( 10·10^6 \) | |
| Kohlenstoff/Graphit | C | 2.1..2.3 | \( 5·10^2..3·10^6 \) | |
| Germanium | Ge | 5.323 | 2.1 | Halbleiter \( 10^{-3} \Omega cm \lt \rho \lt 10^5 \Omega cm \) |
| Silizium | Si | 2.336 | \( 1·10^{3} \) | |
| Galliumarsenid | GaAs | 5.31 | 5000 | |
| Pertinax Epoxidharz | 1.35 | \( 1·10^{-11} \) | Isolatoren \( 10^5 \Omega cm \lt \rho \) | |
| Glas | \( SiO_2 \) | \( 1·10^{-13}\) | ||
| SiliziumNitrid | \( Si_3N_4 \) | 3.35 | \( 1·10^{-10} \) | |
| Polystyrol | PS | \( 1·10^{-16} \) |
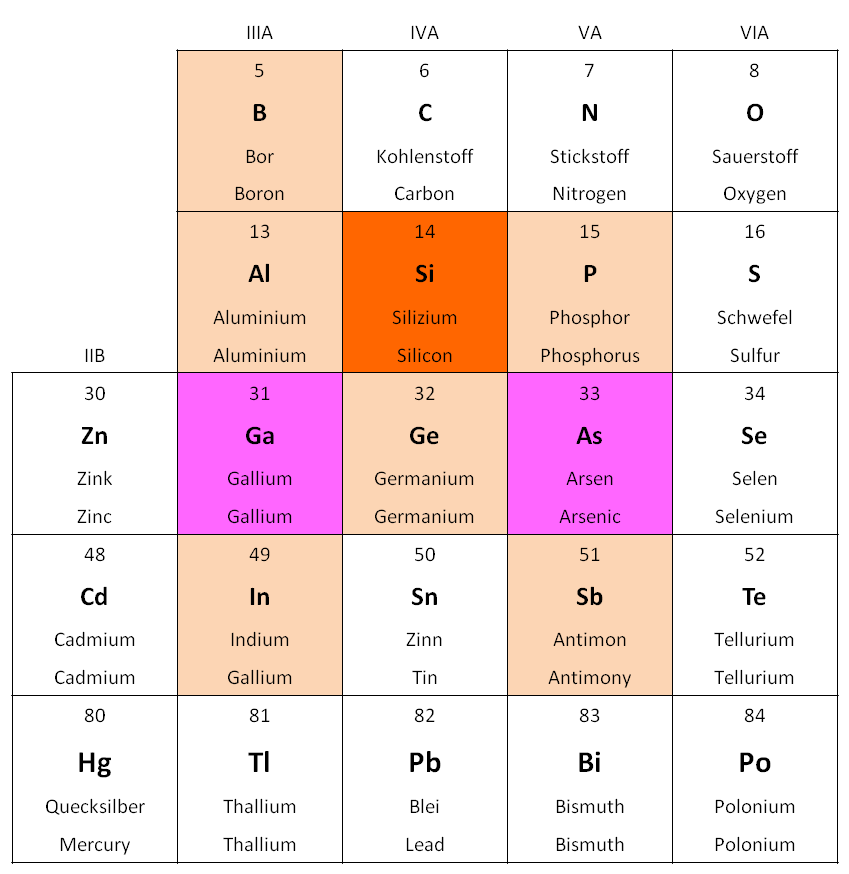
Halbleiter im Periodensystem
|
|
Anwendungen von Halbleiterwerkstoffen
| Anwendung/Bauelemente | Halbleiterwerkstoffe |
| Diode, Transistor, integrierter Schaltkreis | Ge, Si, GaAs |
| Dehnungsmessstreifen | Ge, Si |
| NTC-Widerstand | Si, Ge, GaAs |
| LED, Display | SiC, GaP, GaAs, InAs, InSb |
| Laserdiode | GaAs, InAs, InSb |
| Fotoelement, Solarzelle, LDR | Si, GaAs, CdS, CdSe |
| Hallgenerator, Feldplatte | InSb, InAs |
http://www.elektronik-kompendium.de/sites/grd/0112071.htm
Atome und freie Ladungsträger
| Einheit | Si | Ge | GaAs | |
| Atome je Volumeneinheit | cm-3 | 4.99·1022 | 4.42·1022 | 4.43·1022 |
| Bandabstand Wg | eV | 1.11 | 0.67 | 1.43 |
| Eigenleitungsdichte ni bei 300K | cm-3 | 1.5·1010 | 2.3·1013 | 1.3·106 |
In einem Würfel mit einer Kantenlänge von 1 cm sind 4.99·1022 cm-3 Atome.
Das sind grob gerechnet 40 Millionen Atome entlang einer Kante.
Heutzutage werden integrierte Halbleiter mit einer Strukturgröße von 10 nm hergestellt.
Auf einer Länge von 10 nm sitzen dann 40 Atome.
Die Eigenleitungsdichte ist sehr stark temperaturabhängig.
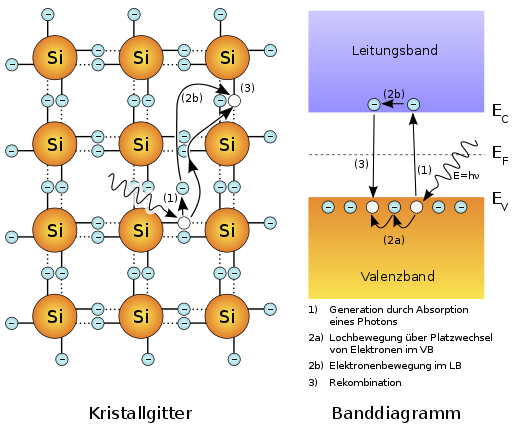
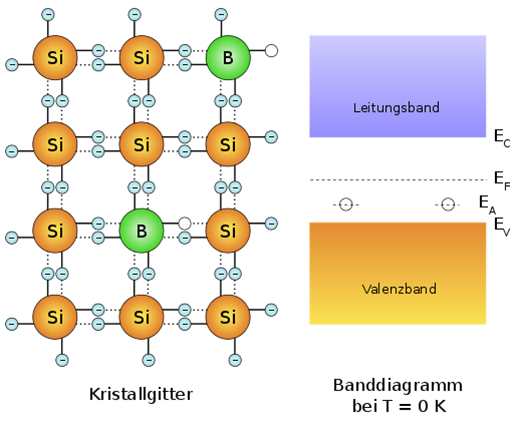
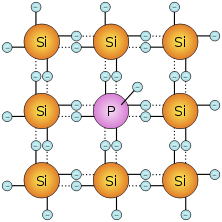
Die Bilder rechts dienen zur stark vereinfachten Veranschaulichung eines Halbleiters.
Im Bild des Kristallgitters wird das wirkliche 3 dimensionale Gitter 2 dimensional gezeichnet, damit man sieht, dass jedes Siliziumatom mit 4 anderen Siliziumatomen eine Bindung eingeht, um 8 Elektronen auf der äußeren Schale zu haben.
Thermische Energie kann ein Elektron aus der Bindung befreien und führt zu beweglichen Elektronen und beweglichen Löchern.
Ein abstrakteres Modell ist das Bändermodell rechts daneben, in dem verschiedene Energieniveaus betrachtet werden.
Das sind grob gerechnet 40 Millionen Atome entlang einer Kante.
Heutzutage werden integrierte Halbleiter mit einer Strukturgröße von 10 nm hergestellt.
Auf einer Länge von 10 nm sitzen dann 40 Atome.
Die Eigenleitungsdichte ist sehr stark temperaturabhängig.
Die Bilder rechts dienen zur stark vereinfachten Veranschaulichung eines Halbleiters.
Im Bild des Kristallgitters wird das wirkliche 3 dimensionale Gitter 2 dimensional gezeichnet, damit man sieht, dass jedes Siliziumatom mit 4 anderen Siliziumatomen eine Bindung eingeht, um 8 Elektronen auf der äußeren Schale zu haben.
Thermische Energie kann ein Elektron aus der Bindung befreien und führt zu beweglichen Elektronen und beweglichen Löchern.
Ein abstrakteres Modell ist das Bändermodell rechts daneben, in dem verschiedene Energieniveaus betrachtet werden.
Modell Leitfähigkeit
- Elektronen und Löcher dienen dem Ladungstransport bei Halbleitern.
- Spezifische elektrische Leitfähigkeit ? \( \kappa \) (kappa)
- \( \kappa = e \mu_n n + e \mu_p p \)
- n,p Anzahl der freien Ladungsträger
- n Elektronen, p Löcher
- \( \mu_n, \mu_p \) Beweglichkeit
- \( \mu_n, \mu_p \) Beweglichkeit
- Die Beweglichkeit ist abhängig von der Kristallstruktur und dem Material.
Eigenleitungsdichte (intrinsic carrier density)
- Die Temperaturabhängigkeit der Eigenleitungsdichte ergibt sich nach der Fermi-Dirac-Statistik: \( n_i^2=B·T^3·exp^{-\frac{W_g}{kT}} \)
- Wg: Bandabstand
- ni0:Eigenleitungsdichte bei T0
- k: Boltzmannkonstante 8.62·10-5 eV/K
- Einheit: Anzahl pro cm3: cm-3
- Massenwirkungsgesetz \( n_i^2=n·p \)
Intrinsic Carrier Concentration
|
Temperature from 500 K (1000/500 = 2) to 200 K (1000/200 = 5). |
|
Die Anzahl freier Ladungsträger ist stark temperaturabhängig.
Statistischer Process: Generation und Rekombination.
Materialgrößen: Lebensdauer, Diffusionslänge
Bändermodell
|
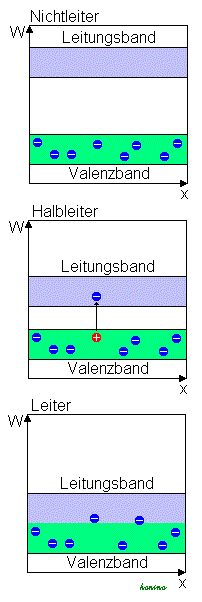 Quelle: Wikipedia Bändermodell |
Rückblick
- Neue Begriffe?
- Welche Halbleiter gibt es?
- Was sind Eigenschaften von Halbleitern?
- Wie wird die Eigenleitungsdichte berechnet?
- Was sind Leitungs- und Valenzband?
Wichtige Eigenschaften: Formelsammlung
| Einheit | Si | Ge | GaAs | |
| Atome je Volumeneinheit | cm-3 | 4.99·1022 | 4.42·1022 | 4.43·1022 |
| Bandabstand Wg | eV | 1.11 | 0.67 | 1.43 |
| Eigenleitungsdichte ni bei 300K | cm-3 | 1.5·1010 | 2.3·1013 | 1.3·106 |
| B | K-3cm-6 | 1.08·1031 | 2.31·1030 | 1.27·1029 |
- Widerstand \( R=\frac{\rho l}{A}=\frac{l}{\kappa \cdot A}=\frac{l}{e(\mu_n n + \mu_p p) \cdot A} \)
- Spezifische elektrische Leitfähigkeit ? \( \kappa \) (kappa)
- Eigenleitungsdichte ni: ni = n0 = p0
- Massenwirkungsgesetz: ni2 = n· p