Elektronik 3

03 Halbleiter

Prof. Dr. Jörg Vollrath

02 Halbleiter

Video der 3. Vorlesung

Länge: 00:47:15

0:0:0 Rückblick

0:2:26 Dotierung

0:4:34 Aktivierung der Dotierstoffatome

0:4:34 Alle Störstellen sind ionisiert

0:6:39 Bändermodell

0:8:37 Beispiel Elektronen- und Löcherdichte

0:10:34 Überlagerung von Dotierstoffen

0:14:52 Lösungsdiskussion

0:16:14 Spezifische Leitfähigkeit

0:18:4 Ladungsträgerbeweglichkeit

0:21:24 Leitfahigkeit Beispiel

0:24:43 Zeitabschätzung

0:26:25 Umrechnungen cm, mm, um, nm

0:27:35 Vernachlässigbare Größen

0:29:40 Nachdenken über die Lösung

0:31:40 Übungsaufgaben

0:32:50 Realistische Werte der Aufgabe?

0:34:5 Ladungsträgertransport Drift, Diffusion

0:38:15 Generation und Rekombination

0:40:17 Differentialgleichungen des Halbleiters

0:41:50 Bauteilsimulator

0:43:35 MOS Transistor

0:45:50 Reflexion der Ihnhalte

0:46:50 Wichtige Gleichungen

Rückblick

Wie gross ist die spezifische Leitfähigkeit von Si, Ge, GaAs?
Was ist ein n-Typ (Elektronen), p-Typ (Löcher), direkter, indirekter Halbleiter?
Dotierung (Einbringen von Fremdatomen)
$\mu_n, \mu_p$ Beweglichkeit
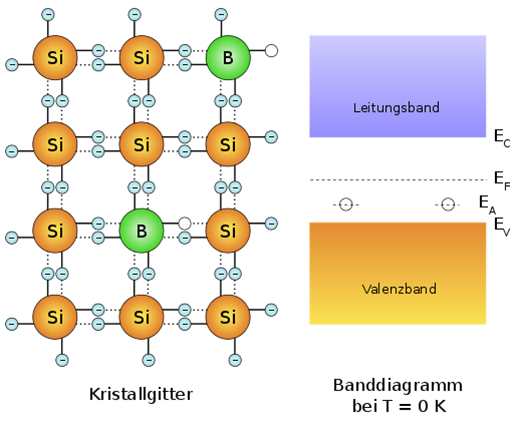
Bandlücke, Bandgap, Bandabstand (0.6..1.5eV), Bänderdiagramm/modell, Leitungsband, Valenzband
Eigenleitungsdichte (intrinsic carrier density), Elektronendichte, Löcherdichte
Massenwirkungsgesetz
Die Anzahl freier Ladungsträger ist stark temperaturabhängig.
In einem Halbleiter gibt es statistische Prozesse: Generation und Rekombination.
Materialgrößen: Lebensdauer, Diffusionslänge
Atome je Volumeneinheit 4..5·10²² cm^-3
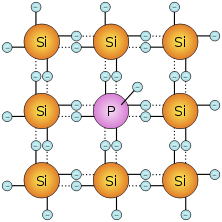
Dotierung

Dotierung

Dotierung nennt man das Einbringen von Fremdatomen
Akzeptorband

3 wertiges Element
Frei bewegliche Löcher

Donatorband

5 wertiges Element
Frei bewegliche Elektronen

Störstellenerschöpfung

Alle Störstellen ionisiert.
p-Halbleiter

p=N_A=N_A^-

n-Halbleiter

n=N_D=N_D⁺

Raumtemperatur
Normalfall

Quelle Wikipedia Defektelektron Dotierung

Dotierung

Störstellenreserve

Niedrige Temperatur T<70K
p+

Bilder schematisch:

Anzahl der Fremdatome sehr hoch
Dotierungskonzentration:
1·10¹⁴cm^-3.. 1·10²¹cm^-3

Beispiel:

3 dimensionaler Kristall Silizium:
Dotierung: 1·10¹⁸cm^-3 Phosphor
Siliziumatome: 4.99 ·10²²cm^-3
1 Phosphoratom auf 50000 Siliziumatome

Was passiert, wenn N_A und N_D vorhanden sind?

Quelle Wikipedia Defektelektron Dotierung

Beispiel

Ein Si-Halbleiter ist mit 1·10¹⁸cm^-3 Bor und 4 ·10¹⁷cm^-3 Phosphor dotiert. Wie groß ist die Löcherdichte und Elektronendichte bei Raumtemperatur und Störstellenerschöpfung?

N_A = 1·10¹⁸cm^-3
N_D = 4 ·10¹⁷cm^-3
N_D < N_A
Störstellenerschöpfung:
p = N_A - N_D = 1·10¹⁸cm^-3 - 4 ·10¹⁷cm^-3 = 6 ·10¹⁷cm^-3
Massenwirkungsgesetz:

$n_i^2=n·p$

$n = \frac{n_i^2}{p} =\frac{1.5·10^{10}cm^{-3} · 1.5·10^{10}cm^{-3}}{6 ·10^{17}cm^{-3}} = 375cm^{-3}$

Ladungsträgerbeweglichkeit
Mobility in Doped Semiconductors

Mobility:

$\mu_n = 92 + \frac{1270}{1+\left( \frac{N_T}{1.3 \cdot 10^{17}} \right)^{0.91}}$

$\mu_p = 48 + \frac{447}{1+\left( \frac{N_T}{6.3 \cdot 10^{16}} \right)^{0.76}}$

Beispiel:Leitfähigkeit

Auf einem Siliziumchip sind integrierte Widerstände mit einer Phosphordotierung von

$4·10^{17}cm^{-3}$ realisiert. Die Widerstände sind

$20 \mu m$ lang,

$4 \mu m$ breit und

$2 \mu m$ tief.
Berechnen sie den spezifischen Widerstand , den spezifischen Leitwert und den Widerstand des dotierten Gebietes bei Raumtemperatur.

$\mu_p= 190 cm^2V^{-1}s^{-1}, \mu_n=460cm^2V^{-1}s^{-1}$

$n=N_D= 4·10^{17}cm^{-3}$

$n_i^2=n·p$

$p=\frac{n_i^2}{n}=\frac{1.5·10^{10}cm^{-3}1.5·10^{10}cm^{-3}}{4·10^{17}cm^{-3}}=563cm^{-3}$

$\kappa = e \mu_n n + e \mu_p p = 29.4 \Omega^{-1}cm^{-1}$

$\rho = \frac{1}{\kappa} = 0.034 \Omega cm$

$R=\frac{\rho l}{A}=\frac{l}{\kappa A} = \frac{l}{e (\mu_n n + \mu_p p)A }$

$R=\frac{20·10^{-4}cm}{1.6·10^{-19}C (460cm^2V^{-1}s^{-1}4·10^{17}cm^{-3} + 200cm^2V^{-1}s^{-1}563cm^{-3})4·10^{-4}cm·2·10^{-4}cm}$

$R = 849 \Omega$

Beispiel:Nachdenken über die Lösung

Dotierung:

$4·10^{17}cm^{-3}$
Geometrie:

$20 \mu m$ lang,

$4 \mu m$ breit und

$2 \mu m$ tief
Beweglichkeit und Einheit:

$\mu_p= 190 cm^2V^{-1}s^{-1}, \mu_n=460cm^2V^{-1}s^{-1}$
Der Anteil der Minoritäten an der Leitfähigkeit ist vernachlässigbar.
µ_n n >> µ_p p

Ergebnis: 849 Ω

Ladungsträgertransport

Ein elektrisches Feld bewegt Ladungsträger:
Feldstrom, Driftstrom (Drift current)
Eindimensionale Stromdichte für Elektronen

$j_n^{drift} = Q_n v_n = (-q·n)(-\mu_nE)$

$j_n^{drift} = qn\mu_nE$

$[A/cm^2]$

$j_T^{drift} = j_n + j_p = q(n\mu_n + p\mu_p)E$
This defines electrical conductivity:

$\sigma = q(n \mu_n + p \mu_p) (\Omega cm)^{-1}$
Resistivity

$\rho$ is the reciprocal of conductivity:

$\rho = \frac{1}{\sigma} (\Omega cm)$

Ein Konzentrationsgradient bewegt Ladungsträger
Diffusionsstromdichte (diffusion current)

$j_n^{diff} = q D_n\frac{\delta n}{\delta x}$

$[A/cm^2]$
Quelle Jaeger Blalock Microelectronic

Was bedeuten die Gleichungen?
Wie kann man Sie physikalisch interpretieren

Ladungsträgergeneration und Rekombination

Mechanismen für die Elektronen-Loch-Paarbildung

Thermische Generation G_th
Leckstrom

Fotogeneration G_Ph
Solarzelle, Photozelle

Stoßionisation G_av
Durchbruch, Ausfall elektronische Bauteile

$G = G_{th}+ G_{Ph} + G_{av}$

$G_{th}=-R=\frac{n_i^2-np}{\tau_p(n+n_1)+\tau_n(p+p1)}$

$\tau_n, \tau_p,$ Elektronenlebensdauer

Ladungsträgerkontinuität

$\frac{\delta J_p}{\delta x} = - q \left(\frac{\delta p(x)}{\delta t}-G\right)$

$\frac{\delta J_n}{\delta x} = q \left(\frac{\delta n(x)}{\delta t}-G\right)$

Kontinuitätsgleichung

Zeitabhängigkeit $\delta t$

Differentialgleichungen für Halbleiter

Variablen I, U ( $\Psi$ ,E) abhängig von n, p

Beschreibung des elektrischen Verhaltens

Poissongleichung: U, E

$\frac{d(\epsilon_H E)}{dx} = \rho = q(N_D^+-N_A^-+p-n)$

Kontinuitätsgleichung

$\frac{\delta J_p}{\delta x} = - q \left(\frac{\delta p(x)}{\delta t}-G\right)$

$j_p = q\mu_p p \left(E - V_T \frac{1}{p}\frac{\delta p}{\delta x} \right)$

$\frac{\delta J_n}{\delta x} = q \left(\frac{\delta n(x)}{\delta t}-G\right)$

$j_n = q\mu_n n \left( E + V_T \frac{1}{n}\frac{\delta n}{\delta x} \right)$

$J =J_n+J_p$

Analytische Lösung für Sonderfälle, Numerische Lösung

Die Poissongleichung verbindet Ladung und elektrisches Feld.
Die Kontinuitätsgleichung führen eine örtliche Stromdichtenänderung auf eine zetiliche Änderung der Ladungsträgerkonzentraztion zurück.
Die Stromdichte wird von dem Driftstrom und Diffusionsstrom bestimmt.

Device Simulator

Numerische Lösung der Gleichungen

Ladungsträgerkonzentration
Ströme
Potential

SILVACO: PISCES
Synopsys: Sentaurus
Selberherr: MINIMOS
GNU Archimedes
TCAD and Device Simulation

PISCES Device Simulator Download

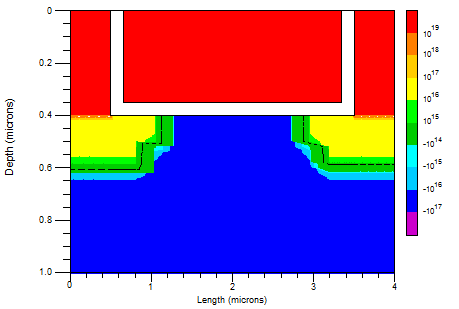Quelle: PISCES Transistor Simulation displayed with postmini

Zusammenfassung und Ausblick

Formulieren Sie Fragen und Antworten zu folgenden Begriffen

Halbleiter

Spezifischer Widerstand

Anzahl Ladungsträger, Beweglichkeit

Bändermodell
Dotierung:

Akzeptoren (Löcher)
Donatoren (Elektronen)

Strom

Diffusionsstrom: Konzentrationsgradient
Driftstrom: Elektrisches Feld

Welche englischen Begriffe haben Sie gelernt?

Weiter mit:

Der pn-Übergang, die Diode

Elektronische Schaltungstechnik, Reinhold: Kapitel 3, S. 41-64
Microelectronic, Jaeger: Chapter 3, page: 75-133

Wichtige Gleichungen: Ergänzen Sie!

Widerstand

Spezifische elektrische Leitfähigkeit? (kappa)

Eigenleitungsdichte n_i:

Massenwirkungsgesetz:

Elektronen- und Löcherkonzentration im dotierten Halbleiter:

Widerstand

$R=\frac{\rho l}{A}=\frac{l}{\kappa A} = \frac{l}{e (\mu_n n + \mu_p p)A }$

Spezifische elektrische Leitfähigkeit? (kappa)

$\kappa = e \mu_n n + e \mu_p p$

$[ \Omega^{-1}cm^{-1} ]$

Eigenleitungsdichte n_i:

_i

₀

Massenwirkungsgesetz:

${n_{i}}^{2} = n \cdot p$

Dotierter Halbleiter:

_D

_A

_D

Nächste Vorlesung

04 Diode

2020 09 07 Elektronik 3 03 Halbleiter Prof. Dr. Joerg Vollrath

Elektronik 3

03 Halbleiter

Prof. Dr. Jörg Vollrath

Video der 3. Vorlesung

Rückblick

Dotierung

Dotierung

Beispiel

Ladungsträgerbeweglichkeit Mobility in Doped Semiconductors

Beispiel:Leitfähigkeit

Beispiel:Nachdenken über die Lösung

Ladungsträgertransport

Ladungsträgergeneration und Rekombination

Differentialgleichungen für Halbleiter

Device Simulator

Zusammenfassung und Ausblick

Wichtige Gleichungen: Ergänzen Sie!

Nächste Vorlesung

Ladungsträgerbeweglichkeit
Mobility in Doped Semiconductors