Elektronik 3

05 Diode

Prof. Dr. Jörg Vollrath

04 Diode: Der pn Übergang

Video der 5. Vorlesung

Länge: 00:42:10

0:0:46 Datenblatt

0:0:46 Datenblatt einer Diode

0:2:51 Forward Characteristic

0:3:46 Temperaturabhängigkeit

0:5:6 Diodencharakteristik

0:5:48 Reale Diode

0:6:41 SPICE Diodenmodell

0:8:53 SPICE .model Dioden Anweisung

0:13:42 Bestimmung der Parameter einer Diode

0:15:20 I=(U2-U1)/R

0:15:56 Strommessung mit einem Widerstand

0:18:13 Strommessbereich

0:20:26 Versuch 2 Diode

0:24:31 Sperrbereich

0:25:27 Sperrbereich, Sperrstrom

0:27:46 Bestimmung n im Durchlassbereich

0:32:32 Vereinfachung auf ID = IS exp(U/n(UT))

0:34:11 Berechnung RS mit grossen Strömen

0:40:48 Diodenarten Schaltsymbole

0:42:36 LTSPICE Diodennetzliste

0:43:20 Simulationsergebnis Diodenkennlinien

0:46:47 Lineare Darstellung der Simulationsergebnisse

0:48:6 Berechnung von Diodenspannungen

0:50:6 Lösung

0:54:16 RS Diskussion: Weglassen oder nicht?

0:55:46 10 fA, 1 mA

0:58:13 Ladungsspeicherung in der Sperrschicht

1:1:34 Ladungsspeicherung im Durchlassbereich

1:3:24 Auschalten einer Dioden

1:5:49 Reverse current der Diode beim Abschalten

1:8:4 Einschalten, ausschalten, ladungsträger

1:8:44 Diodengleichungen

1:9:48 0

Rückblick und Ausblick

Differentialgleichungen

Poisson: U,E (n,p, N_A, N_D)
Transportgleichung: J_n,J_p, (E, dn/dx, dp/dx)

Was ist eine Raumladungszone?
Welche Gleichungen werden benötigt um das Strom Spannungsverhalten eines Halbleiters zu beschreiben?
Wie lautet die Diodengleichung?
Wie wird die Weite der Raumladungszone d_S berechnet?
Diffusionsspannung: U_D
Temperaturspannung: U_T =kT/q=0.025V

Heute:

Strom-Spannungskennlinie, Diodenmessung, SPICE Modell, Kapazitäten
Ersatzschaltbilder, Kleinsignalverhalten, Temperaturmessung

Kennlinienparameter

Flussspannung U_F0
Schleusenspannung

Relativ willkürliche Definition
$U_{F0} =U_F |_{I=0.05 I_{max}}$

Maximal zulässiger Durchlassstrom I_max

Erwärmung des Bauelements, Verlustleistung

Sättigungsstrom I_S
Durchbruchsspannung U_BR

Bei der Durchbruchsspannung kommt es zu einer lawinenartigen Generation von Ladungsträgern in der Sperrschicht.
Lawinendurchbruch

Datenblatt

1N4001 ... 1N4007, 1N4007-1300
Silizium Gleichrichter
Nennstrom 1A
Periodische Spitzensperrspannung 50..2000V
Durchlassspannung V_F<1.1V

Bild einer realen Diode

Quelle: Vollrath
Ein Strich markiert die Richtung. Man kann das Diodensymbol auf der Platine erkennen.
Datenblatt 1N400x

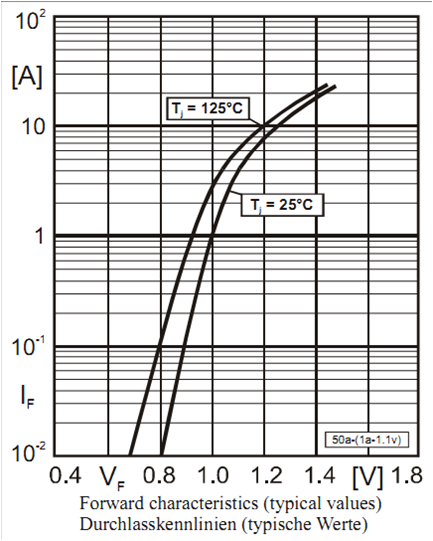Quelle: Datrenblatt

SPICE Diodenmodell

.model 1N914 D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=20n Iave=200m Vpk=75 mfg=Motorola type=silicon)

DC Simulation

Is Saturation current
Rs Series Resistance
N Emission Coefficient
BV, IBV Breakdown voltage

AC, Transient Simulation

Cjo Zero bias junction capacitance
M Grading coefficient
Tt Transit time

Iave Current rating
Vpk Peak voltage rating
Type LED, zener, silicon, Shottky
Mfg Hersteller

$I_D = I_S\left( e^{\frac{q (U - I_D * R_S )}{nkT}}-1\right)$

DiodeModel.asc

Version 4
SHEET 1 880 680
WIRE 16 32 16 0
WIRE 144 112 16 112
WIRE 16 128 16 112
WIRE 144 144 144 112
WIRE 16 240 16 208
WIRE 144 240 144 208
WIRE 144 240 16 240
WIRE 16 272 16 240
SYMBOL res 0 16 R0
SYMATTR InstName RS
SYMATTR Value ""
SYMBOL current 16 128 R0
SYMATTR InstName BI
SYMATTR Value ID=F(VD)
SYMBOL cap 128 144 R0
WINDOW 0 -68 -52 Left 2
SYMATTR InstName C=Cj+CD
SYMATTR Value ""

Quelle: Vollrath

Bestimmung der Parameter der Diodengleichung

Es sollen von einer Diode Is, n und Rs bestimmt werden.

3 Unbekannte, 3 Gleichungen

Der Strom wird mit einem Widerstand gemessen.
Welche Widerstandswerte werden benötigt?

Das Spannungsmessgerät hat eine begrenzte Auflösung: 20mV
Die maximale Spannung der Spannungsversorgung beträgt 10V

$I = \frac{U}{R} = \frac{UOSC2 - UOSC1}{R1}$

R [ $\Omega$ ]	I_min	I_max
10
100
1k
1M

R [ $\Omega$ ]	I_min	I_max
10	2 mA	1 A
100	0.2 mA	100 mA
1k	20 $\mu$ A	10 mA
1M	20 nA	10 $\mu$ A

DiodeR1.asc

Version 4
SHEET 1 880 680
WIRE 176 80 80 80
WIRE 288 80 256 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 OSC1
FLAG 80 80 OSC2
SYMBOL voltage 80 112 R0
SYMATTR InstName V1
SYMATTR Value 1
SYMBOL res 272 64 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1

1M

$\Omega$ ist der Eingangswiderstand des Multimeters/Oszilloskops.

Beispiel: Diodenmessung

An einer idealen Diode mit einem Serienwiderstand RS werden folgende Messungen gemacht.

In welchen Arbeitsbereichen befindet sich die Diode bei den Messungen 1..4?
Bestimmen Sie näherungsweise Is, n und den Serienwiderstand RS. (UT=0.025V)

Messung	1	2	3	4
V_Diode	-2 V	0.5 V	1.4 V	1.6 V
I_Diode	-0.3 nA	11 uA	400 mA	600 mA
Arbeitsbereich

Messung 1:

$I_S = 0.3 nA$ Sättigungsstrom, Sperrstrom
Messung 2:

$I = I_S \left( e^{\frac{U}{n U_T}} \right)$

$n = \frac{U}{ U_T ln \left( \frac{I}{I_S} +1 \right)} = \frac{0.5 V}{ 0.025 V ln \left( \frac{11 \mu A}{0.3 nA} +1 \right)} = 1.9$
Messung 3 und 4:

$U_{Diode3} = n U_T ln \left( \frac{I}{I_S} + 1 \right)$

$= 1.9 \cdot 0.025 V ln \left( \frac{0.4}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_3 - U_{Diode3}}{I_3} = 1 \Omega$

$U_{Diode4} = 1.9 \cdot 0.025 V ln \left( \frac{0.6}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_4 - U_{Diode4}}{I_4} = 0.97 \Omega$

$R_S = \frac{ \Delta U}{ \Delta I} = \frac{U_4 - U_3}{I_4 - I_3} = \frac{0.2 V}{200 mA} = 1 \Omega$

Diodensymbole (LTSPICE) und Gleichung

Vorwärtsbetrieb

$I_D = I_S \left( e^{\frac{q U}{n k T}} - 1 \right)$
Durchbruch

$U_D < BV$

$I_D = - I_S \left( e^{- \frac{q (U+BV)}{n k T}} - 1 + \frac{q BV}{k T} \right)$

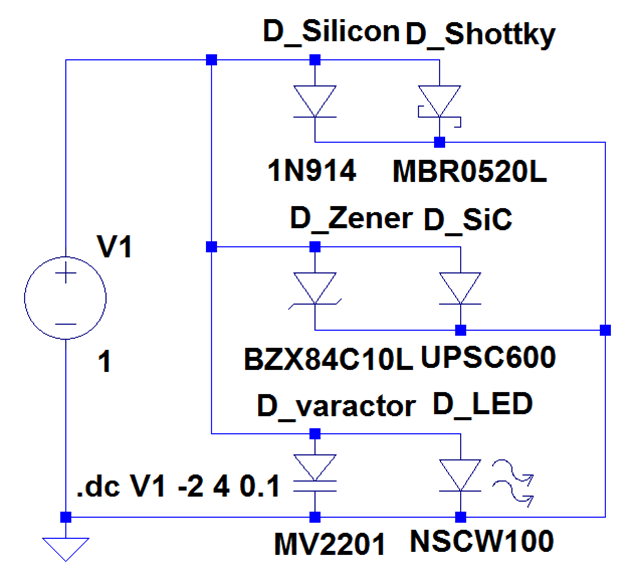Quelle: Vollrath

Dioden_arten_01.asc

Version 4
SHEET 1 880 680
WIRE -320 -128 -432 -128
WIRE -240 -128 -320 -128
WIRE -144 -128 -240 -128
WIRE -144 -64 -240 -64
WIRE -16 -64 -144 -64
WIRE -432 16 -432 -128
WIRE -320 16 -320 -128
WIRE -240 16 -320 16
WIRE -128 16 -240 16
WIRE -128 80 -240 80
WIRE -16 80 -16 -64
WIRE -16 80 -128 80
WIRE -320 160 -320 16
WIRE -240 160 -320 160
WIRE -128 160 -240 160
WIRE -432 224 -432 96
WIRE -240 224 -432 224
WIRE -128 224 -240 224
WIRE -16 224 -16 80
WIRE -16 224 -128 224
WIRE -432 240 -432 224
FLAG -432 240 0
SYMBOL diode -256 -128 R0
WINDOW 0 -24 -22 Left 0
WINDOW 3 -21 85 Left 0
SYMATTR InstName D_Silicon
SYMATTR Value 1N914
SYMBOL schottky -160 -128 R0
WINDOW 0 -10 -20 Left 0
WINDOW 3 -20 86 Left 0
SYMATTR InstName D_Shottky
SYMATTR Value MBR0520L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL zener -256 16 R0
WINDOW 0 -3 -22 Left 0
WINDOW 3 -39 87 Left 0
SYMATTR InstName D_Zener
SYMATTR Value BZX84C10L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL diode -144 16 R0
WINDOW 0 -12 -21 Left 0
WINDOW 3 -15 85 Left 0
SYMATTR InstName D_SiC
SYMATTR Value UPSC600
SYMBOL varactor -256 160 R0
WINDOW 0 -29 -22 Left 0
WINDOW 3 -16 85 Left 0
SYMATTR InstName D_varactor
SYMATTR Value MV2201
SYMATTR Type diode
SYMBOL LED -144 160 R0
WINDOW 0 -5 -23 Left 0
WINDOW 3 -23 83 Left 0
SYMATTR InstName D_LED
SYMATTR Value NSCW100
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL voltage -432 0 R0
SYMATTR InstName V1
SYMATTR Value 1
TEXT -424 200 Left 0 !.dc V1 -2 4 0.1

Dioden in LTSPICE

Netzliste (netlist)
* \Elek3_WS2011\LTSPICE\Dioden_arten_01.asc
D_Silicon N001 0 1N914
D_Shottky N001 0 MBR0520L
D_Zener N001 0 BZX84C10L
D_SiC N001 0 UPSC600
D_varactor N001 0 MV2201
D_LED N001 0 NSCW100
V1 N001 0 1
.model D D
.lib c:\lib\cmp\standard.dio
.dc V1 -2 4 0.1
.backanno
.end
Dioden fangen in der Netzliste mit dem Buchstaben D an.
Es gibt eine Bibliothek (library) standard.dio mit Bauteileigenschaften.

Quelle: Vollrath

Dioden Kennlinie logarithmisch in LTSPICE

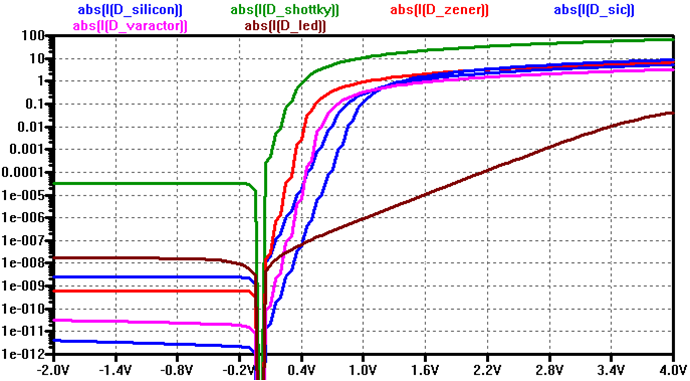
Quelle: Vollrath

	Silizium	Shottky	Zener	SiC	Varaktor	LED
I_s (A)	2.25n	31.7u	0.6n	2p	1.36p	16.9n
n	1.752	0.78	1	1.5	1	6.79

Dioden Kennlinie linear in LTSPICE

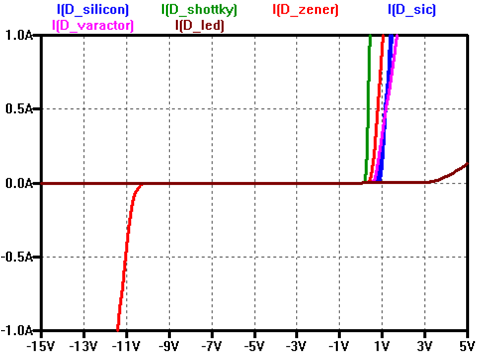
Quelle: Vollrath

Beispiel: Diodenspannung

Berechnen Sie die Diodenspannung für eine Siliziumdiode mit I_s=0.1fA, wenn bei Raumtemperatur ein Strom von 300

$\mu$ A fließt?
Wie groß ist die Diodenspannung für I_s=10fA?
Wie groß ist die Diodenspannung bei einem Strom von 1mA?
V_T = 25mV, n = 1

$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

$U_1 = n V_T ln \left( 1+\frac{I_D}{I_S} \right) = 0.025 ln \left( 1+\frac{3·10^{-4}A}{10^{-16}A} \right) = 0.718V$

$U_2 = n V_T ln \left( 1+\frac{I_D}{I_S} \right) = 0.025 ln \left( 1+\frac{10·10^{-15}A}{10^{-14}A} \right) = 0.603V$

$U_3 = n V_T ln \left( 1+\frac{I_D}{I_S} \right) = 0.025 ln \left( 1+\frac{10^{-3}A}{10^{-16}A} \right) = 0.748V$

Beispiel: Diodensättigungsstrom

An einer Siliziumdiode liegt bei 50°C eine Spannung von 0.736V an und es fließt ein Strom von 2.5mA. Wie groß ist der Sättigungsstrom?

T=(273+50)K=323 K

$V_T = \frac{kT}{q} = \frac{1.38·10^{-23}J/K·323K}{1.6·10^{-19}C} = 27.9mV$

$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

$I_S=\frac{I_D}{e^{\frac{U}{nV_T}}-1} =\frac{2.5mA}{e^{\frac{0.736V}{0.0279V}}-1} = 8.74·10^{-15}A=8.74fA$

Ladungsspeicherung in der Sperrschicht

Sperrschichtkapazität (Junction Capacitance)

C_S, C_J

Abrupter pn-Übergang

$Q_S = q A N_D x_n = - q A N_A x_p$

$d_s = x_n + x_p$

$C_{j0}$ : Diodenkapazität bei 0V

$C_S = A \sqrt{\frac{q \epsilon_H N_A N_D}{2 (N_A+N_D)(U_D-U)}} = \frac{\epsilon_H A}{d_S}$

$C_S = C_J = \frac{C_{J0}}{\sqrt{1-\frac{U}{U_D}}}$

Ladungsspeicherung im Durchlassbereich

Kontinuitätsgleichung

$\tau_D \frac{dI}{dt} = C_D \frac{dU}{dt}$
Diffusionskapazität

$C_D = \frac{d(Q_n+Q_p)}{dU} = \tau_D \frac{I}{U_T}$

Schaltverhalten: Einschalten und Ausschalten

DiodeSchalt.asc

Version 4
SHEET 1 1356 680
WIRE 48 64 32 64
WIRE 128 64 48 64
WIRE 240 64 208 64
WIRE 256 64 240 64
WIRE 32 96 32 64
WIRE 256 96 256 64
WIRE 32 192 32 176
WIRE 144 192 32 192
WIRE 256 192 256 160
WIRE 256 192 144 192
WIRE 144 208 144 192
FLAG 144 208 0
FLAG 48 64 U1
FLAG 240 64 UD
SYMBOL voltage 32 80 R0
WINDOW 3 -50 169 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value PULSE(-2 2 0.1u 1n 1n 0.05u 0.1u)
SYMATTR InstName V1
SYMBOL res 224 48 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL diode 240 96 R0
SYMATTR InstName D1
SYMATTR Value 1N4148X
TEXT -24 280 Left 2 !.tran 0 0.4u 0 0.00001u
TEXT -32 312 Left 2 !.model 1N4148X D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=40n \n+ Iave=200m Vpk=75 mfg=Motorola type=silicon)
TEXT -32 368 Left 2 !;dc V1 -3 3 0.1

SPICE Simulation
t_d Aufladung der Diffusionskapazität
Stationärer Strom I₁

$\tau_S = \tau_D ln\left( 1- \frac{I_1}{I_2} \right)$
t_S Speicherzeit: Entladung der Diffusionskapazität
t_f Abfallzeit t_f ~ C_S(R_V+R_B)

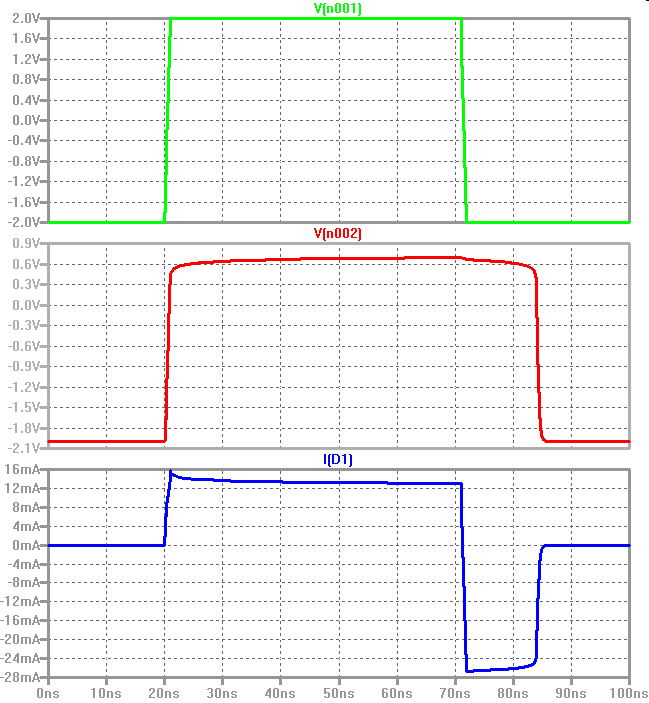td Stromspitze Einschalten, ts konstanter Gegenstrom, tf Abfall des Gegenstroms

Schaltverhalten: Messung

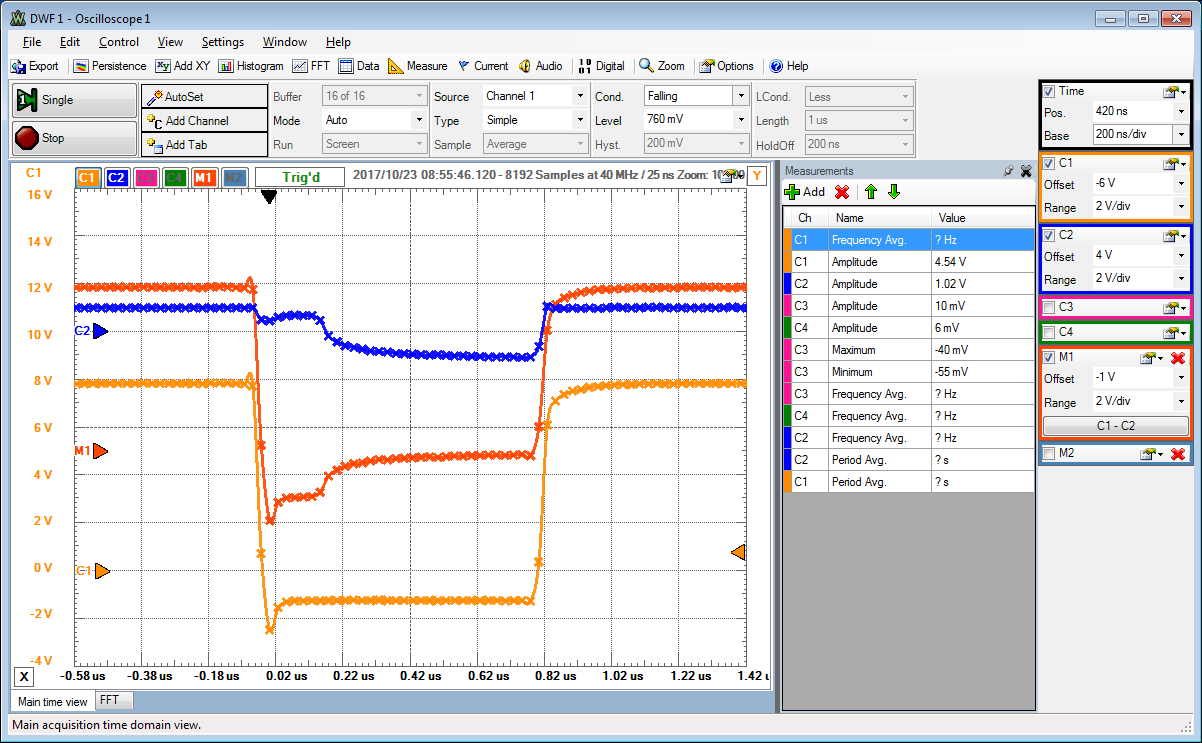
Mittlere Diode aus dem Diodenversuch.
Kleinster Widerstand 100 Ω am Ende des Sockels.
C1 zeigt das Rechteckeingansgsignal zwischen +8 V und -2 V mit einer Frequenz von 500kHz.
C2 zeigt die Diodenspannung.
Ohne eine Speicherladung im pn Übergang, sollte der Strom (M1) durch die Diode bei Sperrspannung sofort Null werden.
Da gespeicherte Ladung vorhanden ist, sieht man noch einen Stromfluss.
Dieses Verhalten entspricht einem Kapazitätsverhalten, man spricht von der Diffusionskapazität.

Diodengleichungen

Symbol

Diode_Symbol.asc

Version 4
SHEET 1 880 680
WIRE -32 48 -144 48
WIRE 144 48 32 48
SYMBOL diode 32 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D1
SYMATTR Value ""
TEXT 64 72 Left 2 !Anode
TEXT -144 72 Left 2 !Kathode

Diodenstrom

$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

Temperaturspannung

$V_T = \frac{kT}{q}$

$( V_T(RT)= 25mV )$

Diffusionsspannung U_D
(Built-in potential)

$U_D = \frac{kT}{q} ln\left(\frac{N_A N_D }{n_i^2} \right)$

Sperrschichtausdehnung (Raumladungszonen)

$d_S = \sqrt{\frac{2 \epsilon_H (U_D-U) \left(N_A + N_D \right)}{q N_A N_D}}$

Sperrschichtkapazität

$C_S = A \sqrt{\frac{q \epsilon_H N_A N_D}{2 (N_A+N_D)(U_D-U)}} = \frac{\epsilon_H A}{d_S}$

$C_S = C_J = \frac{C_{J0}}{\sqrt{1-\frac{U}{U_D}}}$

Diffusionskapazität

$C_D = \frac{d(Q_n+Q_p)}{dU} = \tau_D \frac{I}{U_T}$

Nächste Vorlesung:

Ersatzschaltbilder
Temperaturverhalten

06 Diode

2020 09 07 Elektronik 3 05 Diode Prof. Dr. Joerg Vollrath

Elektronik 3

05 Diode

Prof. Dr. Jörg Vollrath

Video der 5. Vorlesung

Rückblick und Ausblick

Kennlinienparameter

Datenblatt

SPICE Diodenmodell

Bestimmung der Parameter der Diodengleichung

Beispiel: Diodenmessung

Diodensymbole (LTSPICE) und Gleichung

Dioden in LTSPICE

Dioden Kennlinie logarithmisch in LTSPICE

Dioden Kennlinie linear in LTSPICE

Beispiel: Diodenspannung

Beispiel: Diodensättigungsstrom

Ladungsspeicherung in der Sperrschicht

Ladungsspeicherung im Durchlassbereich

Schaltverhalten: Einschalten und Ausschalten

Schaltverhalten: Messung

Diodengleichungen

Nächste Vorlesung: