Elektronik 3

06 Diode

Prof. Dr. Jörg Vollrath

Previous: Dioden Kennlinien

Video der 6. Vorlesung

Länge: 00:42:10

0:00:00 Diode

0:00:23 Rückblick Diode

0:02:50 Ersatzschaltbilder

0:05:38 Berechnung einer Diodenschaltung

0:09:06 Grafische Näherungslösung

0:09:58 Widerstandslastgerade

0:12:59 Rechnung einer Näherungslösung

0:14:54 Kleinsignalbetrachtung

0:16:08 Kleinsignalwiderstand

0:23:14 Ersatzschaltbild der Diode

0:26:03 Flussrichtung, Sperrrichtung

0:27:34 Z-Diode zur Spannungsbegrenzung

0:28:34 UI Kennlinie der Z-Diode

0:31:18 Ersatzschaltbild Z-Diode

0:32:39 Simulation LTSPICE

0:34:39 Z-Diode Beispiel

0:39:38 Quellenumwandlung

0:42:02 Superpositionsansatz

0:43:32 Spannungsteiler

0:47:02 Superposition

0:48:02 Quellenumwandlung

0:51:02 Temperaturmessung mit einer Diode

0:54:43 VPTAT Schaltkreis

0:55:39 Rechenansatz

0:57:42 UDiode Formel

0:59:37 Berechnung eines Wertes

0:59:37 Ergebnis

0:59:39 Ergebnis

0:59:39 MathNotepad

1:01:50 Temperatursensor MAX1617

1:05:44

Veranstaltungen

	12.11.2019 - 15.11.2019 PRODUCTRONICA Weltleitmesse für innovative Elektronikfertigung, München
	10.11.2020 - 13.11.2020 electronica 2018 Components / Systems / Applications München
	25.2. - 27.2.2020 embedded world, Conference Nürnberg, Germany
	Allgäuer Hochschulmesse, April 2020 Kempten

Rückblick und Heute

Diode

Messung, Kennlinie, LTSPICE, Diodenarten
Dynamisches Verhalten: Kapazitäten

Schaltungen und Rechnungen mit Dioden

Ersatzschaltbilder,Kleinsignalverhalten
Schaltverhalten
Temperaturverhalten

Diodenschaltungen

Einweggleichrichter
Graetzschaltung
Villardschaltung
Freilaufdioden
Spannungsstabilisierung

Diodenarten

Z-Dioden, Shottky, pin-Dioden, Kapazitätsdioden, Tunneldioden

Elektronische Schaltungstechnik, Reinhold: Kapitel 3, S. 41-64
Microelectronic, Jaeger: Chapter 3, page: 75-133

Ersatzschaltbilder

Warum benötigt man Ersatzschaltbilder?
Was sind Ersatzschaltbilder?
Wie kann man Ersatzschaltbilder klassifizieren?

Ein elektrisches Bauteil wird mit Hilfe von linearen Elementen: gesteuerten Quellen, Schaltern, Widerständen, Kapazitäten und Induktivitäten modelliert.
Schaltungen mit linearen Bauelementen kann man berechnen.

Kleinsignalersatzschaltbild

Was passiert bei kleinen Spannungs oder Stromänderungen um einen festen Arbeitspunkt?
Diodenspannung 1V
überlagertes Signal 10mV

Großsignalersatzschaltbild

Wie kann man die Diodengleichung durch ideale Bauteile annähern?

Ersatzschaltbild und Kleinsignalverhalten

Ein Widerstand R = 10

$\Omega$ und eine Diode sind in Reihe an einer Spannungsquelle V1 = 1 V angeschlossen.
Der Strom I soll berechnet werden?

$I = I_S\left( e^{\frac{q (V_1 - I * R )}{nkT}}-1\right)$
Dies ist eine nichtlineare Gleichung.
Die Lösung der Gleichung kann nur iterativ durch Ausprobieren erfolgen.

Näherungslösungen:

Grosssignalberechnung
Kleinsignalberechnung

Diode_Messaufbau.asc

Version 4
SHEET 1 880 680
WIRE 144 80 80 80
WIRE 288 80 224 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 SCOPE1DC
FLAG 80 80 SCOPE2DC
SYMBOL voltage 80 112 R0
SYMATTR InstName VAWG1
SYMATTR Value 1
SYMBOL res 240 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1
SYMATTR Value 1N914
TEXT 40 296 Left 2 !.dc VAWG1 0.2 1.0 0.05

Berechnung einer Diodenschaltung: Graphische Lösung

Graphische Lösung:

Was passiert wenn nur die Diode vorhanden wäre?
Wie groß ist der Strom durch den Widerstand bei verschiedenen Diodenspannungen?
Widerstandslastkennline
Wenn 0V an der Diode anliegt fliesst der maximale Strom

$I = \frac{1 V}{ 10 \Omega} = 100 mA$ .
Wenn 1V an der Diode anliegt fliesst kein Strom I = 0.
Zwischen diesen 2 Punkten ist die Kennlinie linear, da der Widerstand ein lineares Bauelement ist. Das Ohmsche Gesetz gilt.

Man kann nun den Arbeitspunkt der Schaltung aus dem Schnittpunkt der Kurven bestimmen.

$U_{Diode} = 0.75 V$ und

$I = 25 mA$

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Die Diodenkennlinie ist sehr steil.
Was passiert, wenn als Diodenspannung 0.7 V angenommen wird?
Dies entspricht einer Spannungsquelle von 0.7 V.

Diodenspannung	Strom
0.7 V	20 mA
0.75 V	25 mA
0.8 V	30 mA

Die Abweichungen zur graphischen Lösung sind gering.
Je größer die Spannung und der Widerstand sind, desto geringer ist die Abweichung.

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Was passiert mit dem Strom, wenn sich die Spannung V1 geringfügig ändert?

Man ersetzt die nichtlineare Diodenkennlinie durch eine Tangente im Arbeitspunkt.
Man ersetzt die Diode durch einen Widerstand.

$r_D = \frac{ \Delta U}{ \Delta I} = \frac{1}{\frac{\delta I}{ \delta U}} = \frac{1}{\frac{\delta I_S \left( e^{\frac{U}{n U_T}} -1 \right)}{ \delta U}}$

$r_D = \frac{1}{\frac{ I_S \left( e^{\frac{U}{n U_T}}\right)}{ n U_T}} = \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}}\right) }$

$r_D \approx \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}} - 1 \right) } = \frac{n U_T}{I_{Diode}} = 1 \Omega$

Man kann nun die Stromänderung der Schaltung im Arbeitspunkt mit der Spannungsteilerregel bestimmen.

$\Delta I = \Delta U \cdot \frac{ r_D}{ R + r_D}$

$\Delta I = 0.2 V \cdot \frac{ 1 \Omega }{ 10 \Omega + 1 \Omega} =0.018 mA$

Ersatzschaltbilder

Grosssignalersatzschaltbild:

Diode_GESB.asc

Version 4
SHEET 1 880 680
WIRE 48 144 0 144
WIRE 128 144 96 144
WIRE 224 144 208 144
SYMBOL voltage 112 144 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 -32 56 VBottom 2
SYMATTR InstName V1
SYMATTR Value 0.7 V
LINE Normal 96 144 48 112

Schalter mit Spannungsquelle (0.7 V)

Kleinsignalersatzschaltbild:

Diode_KESB.asc

Version 4
SHEET 1 880 680
WIRE 336 144 304 144
WIRE 448 144 416 144
SYMBOL res 432 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RD
SYMATTR Value ""

Widerstand

$r_D \approx \frac{n U_T}{I_{Diode}}$

Temperaturverhalten der Diode

Sperrstrom und Durchlassstrom steigen mit der Temperatur.

$I_D = I_S \left( e^{\frac{U}{nU_T}} -1 \right)$

$I_S \sim n_i^2 =B·T^3·exp^{-\frac{W_g}{kT}}$

$V_T \sim T$
Die dargestellte Kennlinie hat für positive Werte eine andere y Achsenskala als für negative Werte.

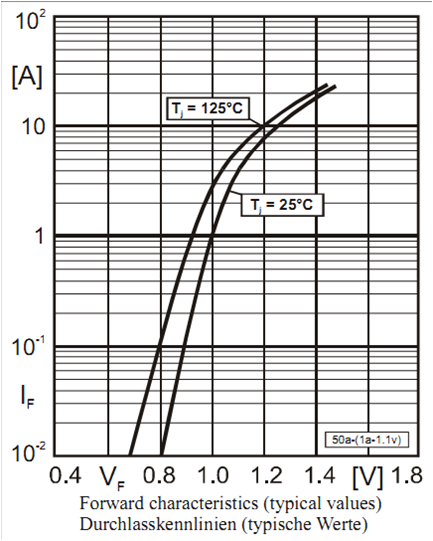Quelle: Datenblatt

Beim automatischen Testen von integrierten Schaltkreisen könen die Schutzdioden an den Pins zur Messung der Testtemperatur benutzt werden. Bei einem konstanten Strom wird die Spannung gemessen.
Dadurch wird sichergestellt, dass man wirklich die Solltemperatur für den Test erreicht hat.

Temperaturmessung mit Diode

Es soll untersucht werden ob die Spannung V_PTAT der folgenden Schaltung direkt proportional zur Temperatur ist.

$k = 8.62·10^{-5} eV/K = 1.38·10^{-23}J/K$
(PTAT: proportional to absolute temperature)
Es werden zwei gleiche Dioden mit den folgenden Strömen verwendet:

$I_{D1} =100 \mu A$ ,

$I_{D2} =10 \mu A$
Wie groß ist die Spannung V_PTAT bei T=195K?
Um wieviel mV ändert sich die Spannung bei 1°C Temperaturänderung?

Temperaturabhängigkeit von Diodenströme

$I_{D1} =100 \mu A$ ,

$I_{D2} =10 \mu A$

$I_{D} = I_S \left( e^{\frac{qU}{kT}}-1\right) \approx I_S e^{\frac{qU}{kT}}$

$U = \frac{kT}{q} ln \left( \frac{I_D}{I_S} \right)$

$V_{PTAT} = U_{D1}-U_{D2}=\frac{kT}{q} ln \left( \frac{I_{D1}}{I_{D2}} \right) = \frac{195 K 8.62 \cdot 10^{-5} eV/K}{q} = 38.9mV$

$\frac{\Delta V_{PTAT}}{\Delta T} = \frac{k}{q} ln \left( \frac{I_{D1}}{I_{D2}} \right) = 0.2 mV/K$

Diode_VPTAT.asc

Version 4
SHEET 1 880 680
WIRE 240 32 96 32
WIRE 96 48 96 32
WIRE 240 48 240 32
WIRE 96 160 96 128
WIRE 128 160 96 160
WIRE 240 160 240 128
WIRE 240 160 208 160
WIRE 96 192 96 160
WIRE 240 192 240 160
WIRE 96 288 96 256
WIRE 160 288 96 288
WIRE 240 288 240 256
WIRE 240 288 160 288
WIRE 160 304 160 288
FLAG 160 304 0
SYMBOL current 96 48 R0
SYMATTR InstName I1
SYMATTR Value ID1
SYMBOL current 240 48 R0
SYMATTR InstName I2
SYMATTR Value ID2
SYMBOL diode 80 192 R0
WINDOW 0 23 1 Left 2
SYMATTR InstName D1
SYMATTR Value ""
SYMBOL diode 224 192 R0
SYMATTR InstName D2
SYMATTR Value ""
TEXT 128 160 Left 2 ;VPTAT

MAX1617 Temperatursensor

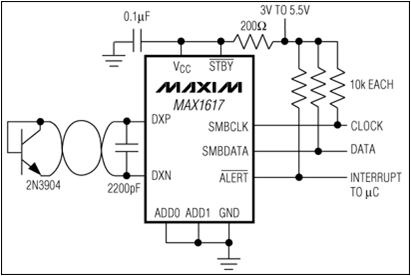Quelle: Datenblatt

Quelle: Datenblatt

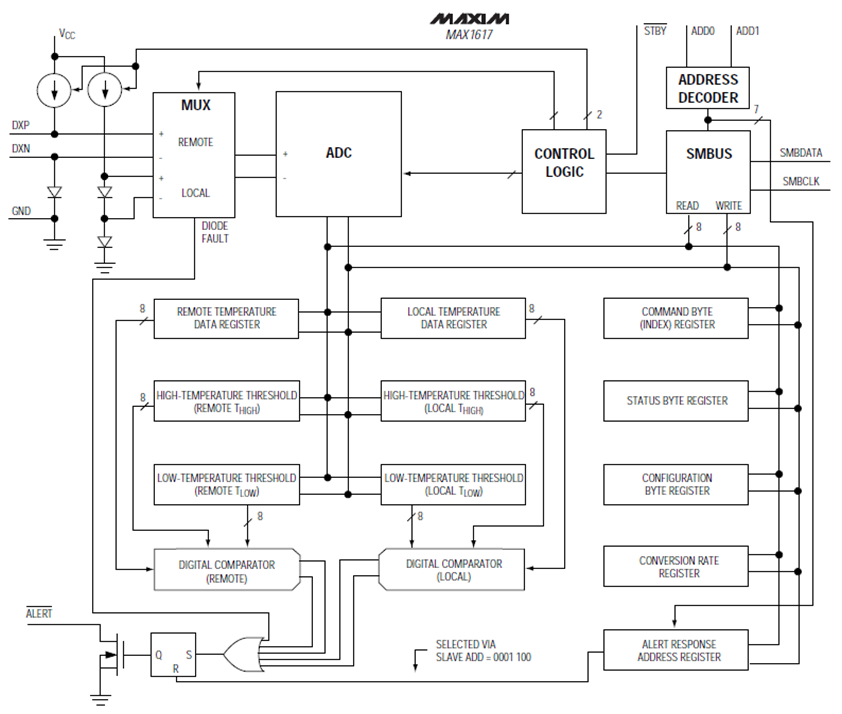Quelle: Datenblatt

2020 09 07 Elektronik 3 06 Diode Prof. Dr. Joerg Vollrath Index

Elektronik 3

06 Diode

Prof. Dr. Jörg Vollrath

Video der 6. Vorlesung

Veranstaltungen

Rückblick und Heute

Ersatzschaltbilder

Ersatzschaltbild und Kleinsignalverhalten

Berechnung einer Diodenschaltung: Graphische Lösung

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Ersatzschaltbilder

Temperaturverhalten der Diode

Temperaturmessung mit Diode

MAX1617 Temperatursensor

Next: