Elektronik 3 14 Verstärkergrundschaltungen Prof. Dr. Jörg Vollrath 13 Stromspiegel

Rückblick und Heute

Stromspiegel

Verstärker
Arbeitspunktberechnung
Zeichnen des Kleinsignalersatzschaltbildes
Berechnung der Spannungsverstärkung

MOSFET oder Bipolartransistor als Verstärker

• Eingangs- und Ausgangsbeschaltung
• Arbeitspunkt: U_BE, U_GS
• Ausgangsstrom: I_DS, I_CE
• Optimierung von Verstärkereigenschaften
• Verstärkung
• Eingangsspannungsbereich
• Ausgangsspannungsbereich
• Leistungsverbrauch
• Frequenzgang

Verstärker Grundschaltungen: Schaltbild

a) Widerstandslast       b) Diodenlast       c) Stromquellenlast       d) Inverter      
Man sieht einen Verstärker mit verschiedenen Lasten:
Widerstand, Transistordiodenschaltung, Stromquellenlast, Inverter
Mit der Widerstandslast und der Diodenlast lassen sich nur kleine Verstärkungen realisieren.
Mit der Stromquellenlast läßt sich eine höhere Verstärkung mit einem vorgegebenen Strom (einer vorgegebenen Leistung) erreichen.
Ein Verstärker mit einer hohen Verstärkung hat einen kleinen Eingangsspannungsbereich.
Die Versorgungsspannung und das Transistorverhalten begrenzen den Ausgangsspannungsbereich.
\( \Delta U_A = v_u \Delta U_E \)
Δ U_A: Ausgangsspannungsbereich
Δ U_E: Eingangsspannungsbereich
v_u: Spannungsverstärkung
Aus Kostengründen oder Leistungsfähigkeit kann es sein, dass man kein Operationsverstärker zur Verfügung hat und eine der Schaltungen verwenden muss.
Bei allen Schaltungen muss sich das Eingangssignal um einen Arbeitspunkt, hier 5 V, bewegen.
Durch Einführen einer negativen Spannung anstatt Masse (0 V), lässt sich der Arbeitspunkt zu 0 V verschieben. Dann ist das Verhalten des Verstärkers aber immer noch sehr stark Versorgugsspannugsabhängig.
Für die Verstärkung von Wechselspannungen kann man den Arbeitsbereiches durch Widerstände festlegen und die Wechselspannung mit einem Kondensator dazu addieren.

Verstärker Grundschaltungen: Kennlinie

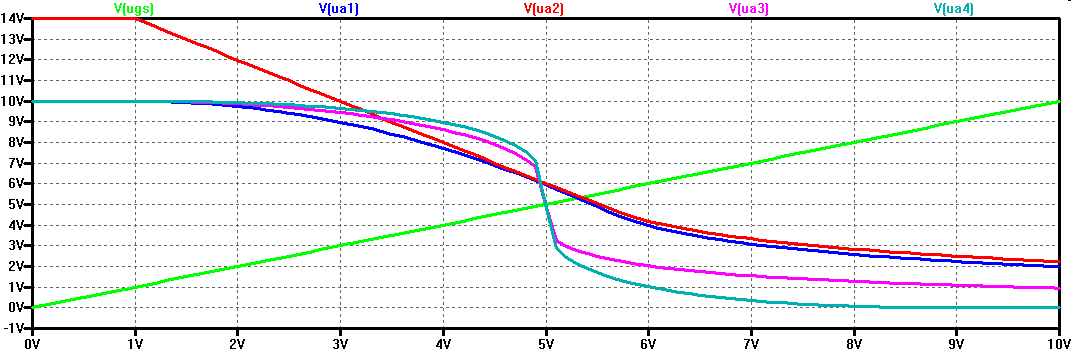
Die DC Kennlinie zeigt das Grosssignalübertragungsverhalten.
Die Steigung der Kurven gibt die mögliche Spannungsverstärkung an.
Die Schaltungen mit der Stromquelle als Last und der Inverter haben die größte Spannungsverstärkung.
Dies kann man mit einer AC Simulation in dB darstellen.
Nur wenn die Gate Sourcespannung sich um 5V bewegt, wirken die Schaltungen als Verstärker.

Verstärker Grundschaltungen: Arbeitspunkt

Durch einen Kondensator wird der Wechselspannunganteil des Eingangssignals zum Gate des Transistor geführt.
Ein Gleichanteil am Gate des Transistors bestimmt den Arbeitspunkt. Dieser wird entweder mit einem Spannungsteiler erzeugt oder durch einen Rückkopplungswiderstand.
Mit einem Widerstand in Serie zum Eingangskondensator kann man die Spannungsverstärkung verkleinern.

Schaltungsanalyse

• Arbeitspunkt (DC)
• C: Unterbrechung
• Spannungsteiler, Stromgleichung, Spannungsgleichung: I_DS, V_GS
• Kleinsignalanalyse
• Superposition: DC Spannungsquellen sind ein Kurzschluss.
• Kapazitäten: Kurzschluss
• Berechnung der Verstärkung (Spannung/Strom)
• Berechnung der Übertragungsfunktion (Frequenzverhalten) mit Kapazitäten

MOSFET Sourceschaltung: Kleinsignalersatzschaltbild 1

Kleinsignalersatzschaltbild Kapazität -> Kurzschluss Induktivität -> Unterbrechung Spannungsversorgung -> Kurzschluss (nach Masse) Eingangs- und Ausgangswiderstand Spannungs- und Stromverstärkung

MOSFET Sourceschaltung: Kleinsignalersatzschaltbild 2

Kleinsignalersatzschaltbild Kapazität -> Kurzschluss Induktivität -> Unterbrechung Spannungsversorgung -> Kurzschluss (nach Masse) Eingangs- und Ausgangswiderstand Spannungs- und Stromverstärkung

Eingangswiderstand	\( r_e = R7 + R_{1} || R_2 \)	Spannungsverstärkung	\( v_u = - g_m\left(r_{D} || R_5 || R_3 \right) \)
Ausgangswiderstand	\( r_a = r_{D} || R_5 || R_3 \)	Stromverstärkung	\( v_i = - g_m \cdot R_{1} || R_2 \)

MOSFET Sourceschaltung SPICE Simulation

NMOS \( KP = 500 \mu AV^{-2} \), \( V_{T0} = 1 V = U_{Th} \) \( V_{DD} = 10 V \), \( \lambda = 0.0167V^{-1} \) Die Größenordnung (kΩ) von R1 und R2 wird durch die Anforderung an den Eingangswiderstand bestimmt. R1 und R2 dürfen nicht zu groß gewählt werden, da Werte größer 1M \( \Omega \) nicht erhältlich sind und Leckströme die Spannung VG bestimmen könnten. Die Spannungsverstärkung wird durch den Übertragungsleitwert ( \( g_{m} \), \( V_{GS} - V_{Th} \) ) und den Ausgangsleitwert ( R5, \( \lambda \) ) festgelegt. Arbeitspunkt, Grosssignal: \( V_{G} = V_{DD} \frac{R_{2}}{R_{2}+R_{1}} = 10 V \frac{ 125 k \Omega}{625 k \Omega} = 2 V \) \( R_{e} = \frac{R_{2} \cdot R_{1}}{R_{2} + R_{1}} = 100 k \Omega \) \( I_{DS} = \frac{K_{N}}{2} \left( V_{GS}- V_{Thn} \right)^{2} = 250\mu A \) \( V_{D} = V_{DD} - R_{5} \cdot I_{DS} = 5V \) Verstärkung, Kleinsignal: Das Eingangssignal V1 wird durch den Spannungsteiler aus R7 und Re verkleinert. \( v_{g} = v_{1} \frac{100 k \Omega}{100 k \Omega + 1 k \Omega} = 0.99 \) Die Spannungsverstärkung der Sourceschaltung ist: \( I_{DS} = \frac{K_{N}}{2} \left( V_{GS}- V_{Thn} \right)^{2} \left( 1 + \lambda V_{DS} \right) \) \( v_{u} = - g_{m} \cdot r_{a} \) \( g_{m} = \frac{2 I_{DS}}{U_{GS}-U_{Th}} = 500 \frac{ \mu A}{V} \) \( r_{a} = r_{DS} || R_{5} || R_{3}= \frac{1}{I_{DS} \lambda} || R_{5} || R_{3} \) \( r_{a} = 240 k \Omega || 20 k \Omega || 100 k \Omega = 15.6 k \Omega \) \( v_{u} = - 500 \frac{ \mu A}{V} \cdot 15.6 k \Omega = 7.79 \) \( A_{V} = 20 log( v_{u} ) = 17.8 dB \) 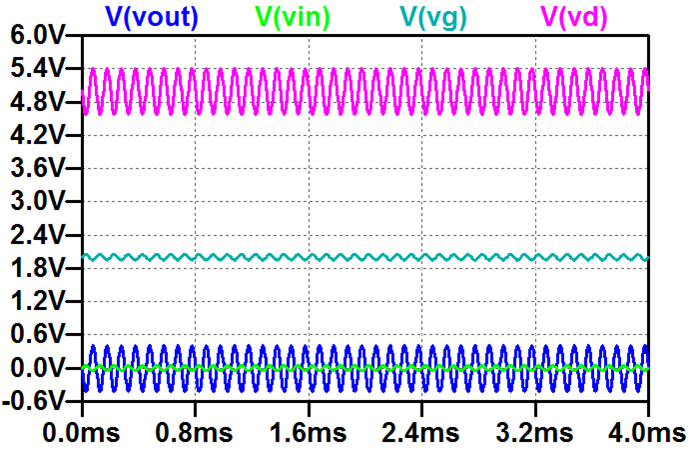Quelle: Vollrath Quelle: Vollrath

Quelle: MOSFET_Sourceschaltung_01.asc

MOSFET Sourceschaltung in SPICE: Grenzfrequenz

Transistormodellparameter:
CGDO = 200 nF/ µm ergibt ohne W,L Angabe (W,L default = 100 µm) C = 20 pF.
Transitfrequenz:
\( f_{t} = \frac{g_{m}}{2 \pi C} \)
\( g_{m} = \frac{2 I_{DS}}{V_{GS} - V_{Th}} = 0.5 mS \)
\( f_{t} = \frac{g_{m}}{2 \pi C} \) = 4 MHz
Grenzfrequenz:
\( f_{g} = \frac{1}{2 \pi R C} = \frac{1}{2 \pi 15.6 k \Omega \cdot 20 pF} = 511 kHz \)

Fragen

Warum erreichen wir nicht die Spannungsverstärkung des Transistors?
\( v_{u} = - \frac{2}{\lambda(V_{GS}-V_{Th})}\)
Wie kann ich die Spannungsverstärkung erhöhen?
Kann es besser sein, wenn die Verstärkung durch externe Widerstände bestimmt wird?
Warum ist ein niedriger Ausgangswiderstand der Verstärkerstufe wichtig?

Grundschaltungen

MOSFET Sourceschaltung in SPICE
(1) Die Spannungen an Gate, Drain, Source, Eingang, Ausgang
(2) Einstellung des Arbeitspunkts mit Widerständen,
(3) Eingangs- und Ausgangssignal werden kapazitiv gekoppelt
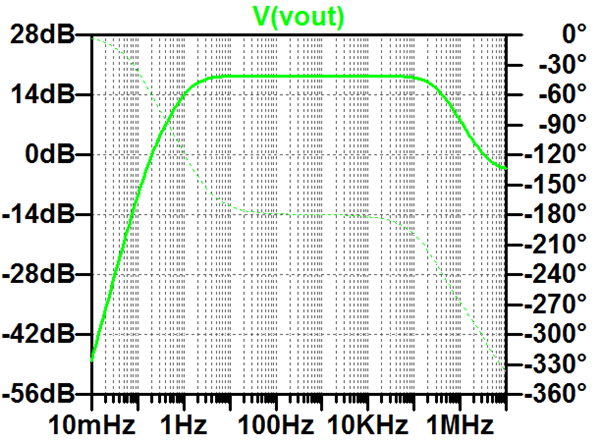
Verstärkung in dB:
\( A_{v} = 20 log \left(\frac{u_a}{u_e}\right) \)
Frequenzgang: Amplitude (dB) und Phase über der logarithmischen Frequenz

MOSFET: Sourceschaltung, Drainschaltung (Sourcefollower), Gateschaltung
Bipolartransistor: Emitterschaltung, Kollektorschaltung, Basisschaltung

Wie sehen diese Schaltungen aus und welche Eigenschaften haben sie?

Arbeitspunkteinstellung (Q point)

MOSFET Drain-Sourcestrom oder Kollektorstrom wählen RD: Ausgangssignal Spannungsbereich ausschöpfen \( R_D \cdot I_D = \frac{V_{DD}-U_{DSmin}}{2} = \frac{V_{DD}-\left(U_{GSmin}-U_{th}\right)}{2} \)	Bipolartransistor \( R_C \cdot I_C = \frac{V_{DD}-U_{BE}}{2} \)
R1,R2: Gate Source Spannung \( U_{GS} = V_{DD} \cdot \frac{R_2}{R_1 + R_2} \)	Basisstrom \( I_{R2} = 2..10I_B \)
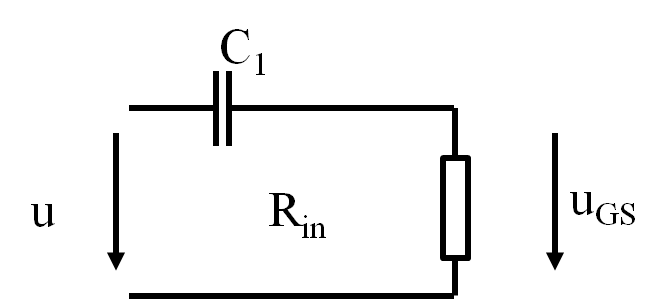
C1,C2: Entkopplung, Hochpass \( f_{gu} = \frac{1}{2 \pi \cdot C_1 R_{in}} \)	Quelle: Vollrath

Einfluss der Signalquelle auf die Verstärkung

Innenwiderstand Spannungsteiler Ri,Re: \( u_e=\frac{u_q}{1+\frac{R_i}{R_e}} \) Verringerte Spannungsverstärkung Stromteiler Ri,Re: \( i_e=\frac{i_q}{1+\frac{R_e}{R_i}} \) Verringerte Stromverstärkung

\( v_u^{'}=\frac{v_u}{1+\frac{R_i}{R_e}} \) \( v_i^{'}=\frac{v_i}{1+\frac{R_e}{R_i}} \)

Zusammenfassung

Das Verhalten der Verstärkerschaltung ergibt sich aus dem Zusammenspiel von:
Transistor
Arbeitspunktbeschaltung
Quelle und
Last

Dabei verschlechtert sich das Verstärkerverhalten.
Das Kleinsignalersatzschaltbild erlaubt es, die Eigenschaften der Verstärkerschaltung zu berechnen.
Widerstände werden zusammengefasst.
Spannungen und Ströme der Quellen mit Last werden berechnet.
Man rechnet von links nach rechts, von der Quelle zur Last.

Beispiel: Arbeitspunkt einer Transistorschaltung

\( Kn = 250 \mu A V^{-2}, Kp = 100 \mu A V^{-2}, \) \( V_{TN} = 0.6 V, V_{TP} = -0.5 V, V_{DD} = 5V , \lambda = 0.001 V^{-1}. \) Bestimmen Sie die Spannungen \( V_{A} \) und \( V_{B} \) und den Strom \( I_{DSM1} \). Transistorgleichung in der Sättigung Knotengleichung PFET: Absolutwerte \( \frac{K_{P}}{2} \left( \left|V_{GS3}\right|- |V_{Thp}| \right)^{2} = \frac{K_{N}}{2} \left( V_{GS2}- V_{Thn} \right)^{2} = \frac{K_{N}}{2} \left( V_{GS1}- V_{Thn} \right)^{2} \) \( V_{DD} = |V_{GS3}| + V{GS2} + V_{GS} \) \( V_{A} = V_{GS1} \), \( V_{B} = 2 \cdot V_{A} \) \( \frac{K_{P}}{2} \left( V_{DD} - 2 \cdot V_{A} - | V_{Thp}| \right)^{2} = \frac{K_{N}}{2} \left( V_{A}- V_{Thn} \right)^{2} \) \( V_{DD} - 2 \cdot V_{A} - | V_{Thp}| = \sqrt{ \frac{K_{N}}{K_{P}}} \left( V_{A}- V_{Thn} \right) \) \( V_{A} \left( \sqrt{ \frac{K_{N}}{K_{P}}} + 2 \right) = V_{DD} - | V_{Thp}| + \sqrt{ \frac{K_{N}}{K_{P}} } V_{Thn} \) \( V_{A} = \frac{V_{DD} - | V_{Thp}| + \sqrt{ \frac{K_{N}}{K_{P}} } V_{Thn}} { \sqrt{ \frac{K_{N}}{K_{P}}} + 2} = 1.52 V \) \( V_{B} = 2 \cdot V_{A} = 3.04 V \), \( I_{DS} = \frac{K_{N}}{2} \left( V_{A}- V_{Thn} \right)^{2} = 106\mu A \)

Quelle: WS2011_Aufgabe_3.asc

Nächstes Mal:

15 Verstärker