Elektronik 315 VerstärkergrundschaltungenProf. Dr. Jörg Vollrath14 Verstärker |
Video 15 Verstärkerschaltungen
|
Länge: 01:08:17 |
0:1:4 Verstärker Grundschaltungen 0:3:5 Diodenlast 0:3:44 Transistorlast 0:4:17 Inverter 0:5:45 Verstärker mit Diodenlast 0:7:46 Kondensator Kurzschluss 0:10:31 PFET Drain und Gate Verbunden 0:13:4 Spannungsverstärkung 0:16:1 Beispiel rechnen 0:18:48 Werkzeuge 0:24:33 IDS M1, M2, M3 0:28:5 VB = 2 VA 0:29:5 Zuerst fehlerhaft: Richtg 1/2 VB 0:31:38 Berechnung VB Korrektur 0:32:44 VB = 3.04V 0:36:50 Anlaoge Schaltungstechnik 0:39:25 Millerkapazität, Äquivalenter entkoppelter Schaltkreis 0:42:49 Cin 0:48:56 Praktische Durchführung im Praktikum 0:50:5 Widerstände zwischen Ein- und Ausgang werden transformiert 0:52:45 Drainschaltung, Sourcefollower 0:57:29 Kaskodenschaltung mit Gateschaltung 1:0:54 Simulationsergebnis 1:3:45 Gateschaltung 1:4:15 Zusammenfassung |
Rückblick und Heute
- Verstärker
- Sourceschaltung
- NF-Kleinsignalverhalten, Frequenzgang, Arbeitspunkt
- Heute:
- Grundschaltungen
- Vergleich der Grundschaltungen
- Millerkapazität
Reinhold: 177, 179, 212
Jaeger: 886-890,1160-1161, 1184
Verstärker Grundschaltungen
Version 4 SHEET 1 1196 708 WIRE 416 112 384 112 WIRE 448 112 416 112 WIRE 768 112 736 112 WIRE 800 112 768 112 WIRE -416 128 -560 128 WIRE -384 128 -416 128 WIRE -352 128 -384 128 WIRE 0 128 -144 128 WIRE 32 128 0 128 WIRE 64 128 32 128 WIRE -560 144 -560 128 WIRE -416 144 -416 128 WIRE -144 144 -144 128 WIRE 448 160 448 112 WIRE 448 160 384 160 WIRE 800 160 800 112 WIRE 800 160 736 160 WIRE 64 176 64 128 WIRE 64 176 0 176 WIRE 336 192 320 192 WIRE 688 192 608 192 WIRE -48 208 -64 208 WIRE -416 240 -416 224 WIRE -320 240 -416 240 WIRE -64 240 -64 208 WIRE 0 240 0 224 WIRE 0 240 -64 240 WIRE 96 240 0 240 WIRE 384 240 384 208 WIRE 384 240 336 240 WIRE 480 240 384 240 WIRE 608 240 608 192 WIRE 736 240 736 208 WIRE 736 240 688 240 WIRE 848 240 736 240 WIRE -560 256 -560 224 WIRE -560 256 -576 256 WIRE -496 256 -560 256 WIRE -144 256 -144 224 WIRE -144 256 -160 256 WIRE -80 256 -144 256 WIRE -560 272 -560 256 WIRE -144 272 -144 256 WIRE -336 288 -416 288 WIRE 80 288 0 288 WIRE 464 288 384 288 WIRE 816 288 736 288 WIRE -496 320 -496 256 WIRE -464 320 -496 320 WIRE -80 320 -80 256 WIRE -48 320 -80 320 WIRE 256 320 256 240 WIRE 256 320 240 320 WIRE 336 320 256 320 WIRE 608 320 608 240 WIRE 608 320 592 320 WIRE 688 320 608 320 WIRE -416 352 -416 336 WIRE -416 352 -560 352 WIRE -336 352 -336 288 WIRE -336 352 -416 352 WIRE 0 352 0 336 WIRE 0 352 -144 352 WIRE 80 352 80 288 WIRE 80 352 0 352 WIRE 384 352 384 336 WIRE 464 352 464 288 WIRE 464 352 384 352 WIRE 736 352 736 336 WIRE 816 352 816 288 WIRE 816 352 736 352 WIRE -416 368 -416 352 WIRE 0 368 0 352 WIRE 384 368 384 352 WIRE 736 368 736 352 FLAG 384 368 0 FLAG 320 192 VBIAS FLAG 480 240 UA3 FLAG 176 320 UGS FLAG 416 112 VDDB FLAG 736 368 0 FLAG 848 240 UA4 FLAG 544 320 UGS FLAG 768 112 VDDC FLAG -416 368 0 FLAG -320 240 UA1 FLAG -384 128 VDD FLAG 0 368 0 FLAG 96 240 UA2 FLAG 32 128 VDDA FLAG -224 256 UGS FLAG -640 256 UGS SYMBOL nmos4 336 240 R0 SYMATTR InstName MN1 SYMBOL pmos4 336 112 R0 SYMATTR InstName M1 SYMBOL nmos4 688 240 R0 SYMATTR InstName MN2 SYMBOL pmos4 688 112 R0 WINDOW 3 60 72 Left 2 SYMATTR InstName M2 SYMBOL nmos4 -464 240 R0 SYMATTR InstName MN3 SYMBOL nmos4 -48 240 R0 SYMATTR InstName MN4 SYMATTR Value2 m=4 SYMBOL pmos4 -48 128 R0 SYMATTR InstName M4 SYMATTR Value2 m=1 SYMBOL res -432 128 R0 SYMATTR InstName R1 SYMATTR Value 1k SYMBOL cap 608 304 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C1 SYMATTR Value 1� SYMBOL res 704 224 R90 WINDOW 0 -4 58 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R2 SYMATTR Value 100k SYMBOL res 352 224 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R3 SYMATTR Value 100k SYMBOL cap 240 304 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C2 SYMATTR Value 1� SYMBOL res -160 128 R0 SYMATTR InstName R4 SYMATTR Value 200k SYMBOL res -160 256 R0 SYMATTR InstName R5 SYMATTR Value 100k SYMBOL cap -160 240 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C3 SYMATTR Value 1� SYMBOL res -576 128 R0 SYMATTR InstName R6 SYMATTR Value 100k SYMBOL res -576 256 R0 SYMATTR InstName R7 SYMATTR Value 100k SYMBOL cap -576 240 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C4 SYMATTR Value 1� TEXT -376 24 Left 2 !.model NMOS NMOS(LEVEL=1 KP=500u VT0=1 LAMBDA=0.002 CGSO=1n CGBO=2n CGDO=200n)\n.model PMOS PMOS(LEVEL=1 KP=500u VT0=-1 LAMBDA=0.002 CGSO=1n CGBO=2n CGDO=200n) TEXT -408 408 Left 2 !;tran 0 2.2u 0.2u TEXT -112 408 Left 2 !.ac oct 10 100 100000k TEXT -496 88 Left 2 !VDD VDD 0 10 TEXT 128 96 Left 2 !VBIAS VBIAS 0 DC 7 TEXT -312 88 Left 2 !VE UGS 0 SINE(5 0.1 10000k) AC 1 TEXT 184 408 Left 2 !;dc VE 0 10 0.1 TEXT 496 96 Left 2 !VDDA VDDA 0 10 TEXT 496 128 Left 2 !VDDB VDDB 0 10 TEXT 496 160 Left 2 !VDDC VDDC 0 10Durch einen Kondensator wird der Wechselspannunganteil des Eingangssignals zum Gate des Transistor geführt.
Ein Gleichanteil am Gate des Transistors bestimmt den Arbeitspunkt. Dieser wird entweder mit einem Spannungsteiler erzeugt oder durch einen Rückkopplungswiderstand.
Mit einem Widerstand in Serie zum Eingangskondensator kann man die Spannungsverstärkung verkleinern.
Verstärker Grundschaltungen mit Diodenlast
Version 4 SHEET 1 1196 708 WIRE 0 128 -144 128 WIRE 32 128 0 128 WIRE 64 128 32 128 WIRE -144 144 -144 128 WIRE 64 176 64 128 WIRE 64 176 0 176 WIRE -48 208 -64 208 WIRE -64 240 -64 208 WIRE 0 240 0 224 WIRE 0 240 -64 240 WIRE 96 240 0 240 WIRE -144 256 -144 224 WIRE -144 256 -160 256 WIRE -80 256 -144 256 WIRE -144 272 -144 256 WIRE 80 288 0 288 WIRE -80 320 -80 256 WIRE -48 320 -80 320 WIRE 0 352 0 336 WIRE 0 352 -144 352 WIRE 80 352 80 288 WIRE 80 352 0 352 WIRE 0 368 0 352 FLAG 0 368 0 FLAG 96 240 UA2 FLAG 32 128 VDDA FLAG -224 256 UGS SYMBOL nmos4 -48 240 R0 SYMATTR InstName MN4 SYMATTR Value2 m=4 SYMBOL pmos4 -48 128 R0 SYMATTR InstName M4 SYMATTR Value2 m=1 SYMBOL res -160 128 R0 SYMATTR InstName R4 SYMATTR Value 200k SYMBOL res -160 256 R0 SYMATTR InstName R5 SYMATTR Value 100k SYMBOL cap -160 240 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C3 SYMATTR Value 1� TEXT -368 -8 Left 2 !.model NMOS NMOS(LEVEL=1 KP=500u VT0=1 \n+ LAMBDA=0.002 CGSO=200n CGBO=2n CGDO=200n)\n.model PMOS PMOS(LEVEL=1 KP=500u VT0=-1 \n+ LAMBDA=0.002 CGSO=200n CGBO=2n CGDO=200n) TEXT -352 320 Left 2 !;tran 0 2.2u 0.2u TEXT -360 384 Left 2 !.ac oct 10 100 100000k TEXT -368 104 Left 2 !VE UGS 0 SINE(5 0.1 10000k) AC 1 TEXT -368 352 Left 2 !;dc VE 0 10 0.1 TEXT -344 144 Left 2 !VDDA VDDA 0 10 |
Version 4
SHEET 1 880 680
WIRE -32 128 -64 128
WIRE 64 128 -32 128
WIRE 336 128 144 128
WIRE 384 128 336 128
WIRE 432 128 384 128
WIRE 480 128 432 128
WIRE 144 160 144 128
WIRE 336 160 336 128
WIRE 432 160 432 128
WIRE -32 208 -32 128
WIRE 64 208 64 128
WIRE -32 320 -32 288
WIRE 64 320 64 288
WIRE 64 320 -32 320
WIRE 144 320 144 240
WIRE 144 320 64 320
WIRE 336 320 336 240
WIRE 336 320 144 320
WIRE 432 320 432 240
WIRE 432 320 336 320
WIRE 336 336 336 320
FLAG 336 336 0
FLAG -64 128 UGS
IOPIN -64 128 In
FLAG 64 128 UGS
FLAG 384 128 VDS
FLAG 480 128 UA2
IOPIN 480 128 Out
SYMBOL res 48 192 R0
SYMATTR InstName R5
SYMATTR Value 100k
SYMBOL res -48 192 R0
SYMATTR InstName R4
SYMATTR Value 200k
SYMBOL res 416 144 R0
SYMATTR InstName RMP
SYMATTR Value {rmp}
SYMBOL res 320 144 R0
SYMATTR InstName RDN
SYMATTR Value 100k
SYMBOL bi 144 160 R0
SYMATTR InstName B1
SYMATTR Value I={gmn} * V(UGS)
TEXT -40 72 Left 2 !.param gmn=2m rmp=10k
TEXT -120 352 Left 2 !VGS UGS 0 SINE(0 0.5 100k) AC 1
TEXT -120 384 Left 2 !.tran 50u
|
1/gmp ist normalerweise kleiner als Rdp.
Durch das Größenverhältnis (Stromverhältnis, β )der Transistoren lässt sich die Verstärkung festlegen.
Mit dieser Schaltung lässt sich nur eine niedrige Verstärkung realisieren (< 10).
Kleinsignalbetrachtung:
v_u = \frac{u_a}{u_e} = - \frac{u_e \cdot g_{mn4} \cdot \frac{1}{g_{dn4} + g_{mp4}}}{u_e} = - \frac{ g_{mn4} }{g_{dn4} + g_{mp4}} \approx - \frac{ g_{mn4} }{g_{mp4}}
Großsignalbetrachtung:
I_{DS} = \beta_{n4} \left( U_{GSN4} - U_{thn} \right)^2 = \beta_{p4} \left( U_{GSP4} - U_{thp} \right)^2
\sqrt{\frac{\beta_{n4}}{\beta_{p4}}} \left( U_{E} - U_{thn} \right) = \left( U_{DD} - U_{A} - U_{thp} \right)
U_{A} = U_{DD} - U_{thp} + \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{thn} - \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{E}
v_u = \frac{u_a}{u_e} = - \frac{u_e \cdot g_{mn4} \cdot \frac{1}{g_{dn4} + g_{mp4}}}{u_e} = - \frac{ g_{mn4} }{g_{dn4} + g_{mp4}} \approx - \frac{ g_{mn4} }{g_{mp4}}
Großsignalbetrachtung:
I_{DS} = \beta_{n4} \left( U_{GSN4} - U_{thn} \right)^2 = \beta_{p4} \left( U_{GSP4} - U_{thp} \right)^2
\sqrt{\frac{\beta_{n4}}{\beta_{p4}}} \left( U_{E} - U_{thn} \right) = \left( U_{DD} - U_{A} - U_{thp} \right)
U_{A} = U_{DD} - U_{thp} + \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{thn} - \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{E}
Verstärker Grundschaltungen mit aktiver Last
Version 4 SHEET 1 1196 708 WIRE 416 112 384 112 WIRE 448 112 416 112 WIRE 448 160 448 112 WIRE 448 160 384 160 WIRE 336 192 320 192 WIRE 384 240 384 208 WIRE 384 240 336 240 WIRE 480 240 384 240 WIRE 464 288 384 288 WIRE 256 320 256 240 WIRE 256 320 240 320 WIRE 336 320 256 320 WIRE 384 352 384 336 WIRE 464 352 464 288 WIRE 464 352 384 352 WIRE 384 368 384 352 FLAG 384 368 0 FLAG 320 192 VBIAS FLAG 480 240 UA3 FLAG 176 320 UGS FLAG 416 112 VDDB SYMBOL nmos4 336 240 R0 SYMATTR InstName MN1 SYMBOL pmos4 336 112 R0 SYMATTR InstName M1 SYMBOL res 352 224 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R3 SYMATTR Value 100k SYMBOL cap 240 304 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C2 SYMATTR Value 1� TEXT 80 -40 Left 2 !.model NMOS NMOS(LEVEL=1 KP=500u VT0=1 \n+LAMBDA=0.002 CGSO=1n CGBO=2n CGDO=200n)\n.model PMOS PMOS(LEVEL=1 KP=500u VT0=-1 \n+LAMBDA=0.002 CGSO=1n CGBO=2n CGDO=200n) TEXT 72 208 Left 2 !;tran 0 2.2u 0.2u TEXT 112 376 Left 2 !.ac oct 10 100 100000k TEXT 80 104 Left 2 !VBIAS VBIAS 0 DC 7 TEXT 80 72 Left 2 !VE UGS 0 SINE(5 0.1 10000k) AC 1 TEXT 80 176 Left 2 !;dc VE 0 10 0.1 TEXT 88 136 Left 2 !VDDB VDDB 0 10 |
Version 4
SHEET 1 880 680
WIRE -32 128 -64 128
WIRE 16 128 -32 128
WIRE 144 128 96 128
WIRE 336 128 144 128
WIRE 384 128 336 128
WIRE 432 128 384 128
WIRE 480 128 432 128
WIRE 144 160 144 128
WIRE 336 160 336 128
WIRE 432 160 432 128
WIRE 144 320 144 240
WIRE 336 320 336 240
WIRE 336 320 144 320
WIRE 432 320 432 240
WIRE 432 320 336 320
WIRE 336 336 336 320
FLAG 336 336 0
FLAG -64 128 UGS
IOPIN -64 128 In
FLAG -32 128 UGS
FLAG 384 128 VDS
FLAG 480 128 UA2
IOPIN 480 128 Out
SYMBOL res 112 112 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R5
SYMATTR Value 100k
SYMBOL res 416 144 R0
SYMATTR InstName RDP
SYMATTR Value {rdp}
SYMBOL res 320 144 R0
SYMATTR InstName RDN
SYMATTR Value 100k
SYMBOL bi 144 160 R0
SYMATTR InstName B1
SYMATTR Value I={gmn} * V(UGS)
TEXT -40 72 Left 2 !.param gmn=2m rdp=100k
TEXT -120 352 Left 2 !VGS UGS 0 SINE(0 0.5 100k) AC 1
TEXT -120 384 Left 2 !.tran 50u
|
Es ist gdp wirksam. Es werden größere Verstärkungen erzielt.
Kleinsignalbetrachtung:
v_u = \frac{u_a}{u_e} = - \frac{u_e \cdot g_{mn4} \cdot \frac{1}{g_{dn4} + g_{dp4}}}{u_e} = - \frac{ g_{mn4} }{g_{dn4} + g_{dp4}}
v_u = \frac{u_a}{u_e} = - \frac{u_e \cdot g_{mn4} \cdot \frac{1}{g_{dn4} + g_{dp4}}}{u_e} = - \frac{ g_{mn4} }{g_{dn4} + g_{dp4}}
Analoge Schaltungstechnik
- Aufteilung in Blöcke
- Arbeitspunkt
- Kleinsignalersatzschaltbild
- Reihenschaltung, Parallelschaltung, Kettenschaltung
- Schrittweises Zusammenfassen
- Vierpolparameter
- Quelle, Innenwiderstand, Lastwiderstand
- Verstärkung, Eingangswiderstand, Ausgangswiderstand
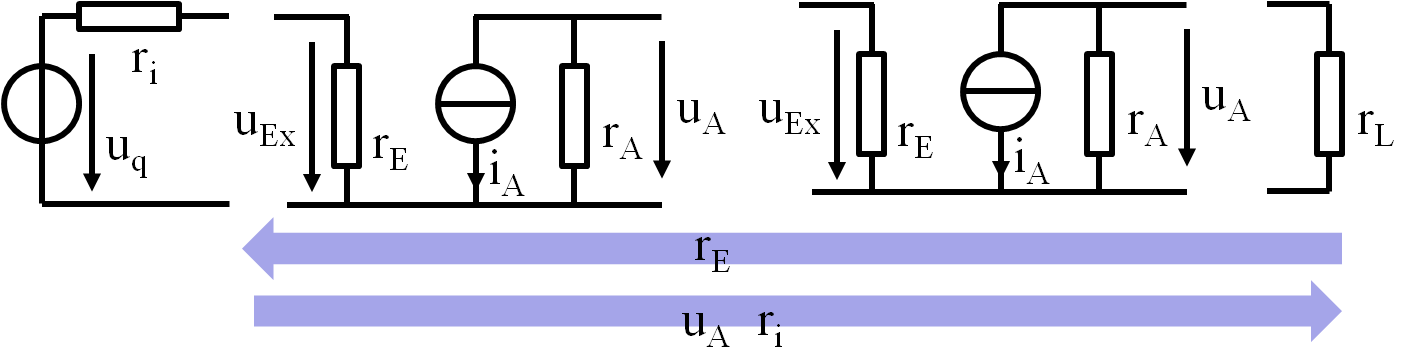
In der analogen Schaltugnstechnik versucht man möglichst einfache Schaltungen
durch Aneinanderreihung von realen Quellen und Lasten aufzubauen.
Das erleichtert die Rechnung und das Verständnis der Schaltungen.
Komplexe Widerstände die Eingang (Gate) und Ausgang (Drain) verbinden, verhindern eine solche einfache Analyse.
Deshalb versucht man diese Elemente durch äquivalente Elemente nur am Eingang und am Ausgang zu ersetzen.
In der folgenden Folie wird das für eine Kapazität durchgeführt.
Das erleichtert die Rechnung und das Verständnis der Schaltungen.
Komplexe Widerstände die Eingang (Gate) und Ausgang (Drain) verbinden, verhindern eine solche einfache Analyse.
Deshalb versucht man diese Elemente durch äquivalente Elemente nur am Eingang und am Ausgang zu ersetzen.
In der folgenden Folie wird das für eine Kapazität durchgeführt.
Frequenzeigenschaften und Millerkapazität
|
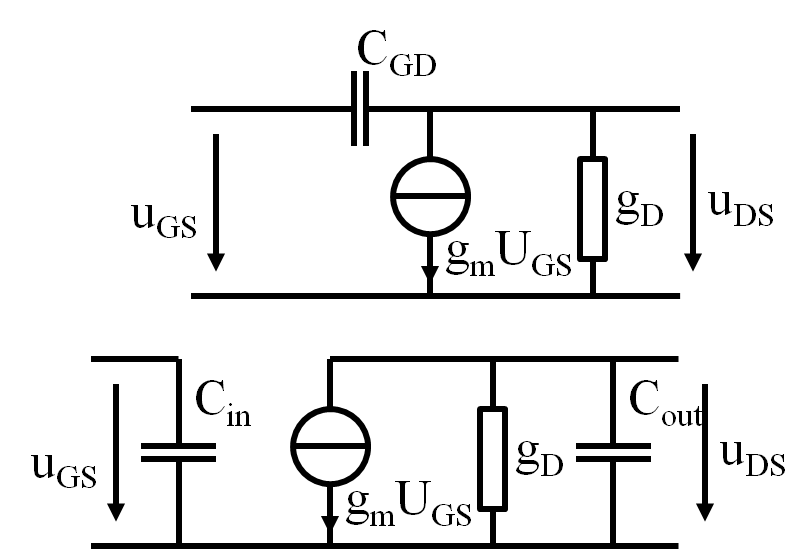
Für eine einfacherer Betrachtung möchte man die Kapazität CGD durch eine
äquivalente Eingangskapazität Cin und Ausgangskapazität Cout ersetzen. j \omega C_{in} = \frac{\underline{I}_{in}}{\underline{U}_{in}} = \frac{\left( \underline{U}_{in} + \frac{g_m \underline{U}_{in}}{g_D}\right) j \omega C_{GD}}{\underline{U}_{in}} C_{in} = \left( 1 + \frac{g_m}{g_D} \right) C_{GD} = \left( 1 + |v_{u}| \right) C_{GD} C_{out} = C_{GD} Die äquivalente Kapazität C_{in} ist viel größer als C_{GD} . MillereffektDiese Kapazität begrenzt die maximale Frequenz bei der noch eine Verstärkung erzielt werden kann. |
|
U_{in} = I_{in} \left( \frac{1}{j \omega C_{GD}} + \frac{1}{g_{D}} \right) - U_{in} \cdot \frac{g_{m}}{g_{d}}
U_{in} \left( 1 + \frac{g_{m}}{g_{d}} \right) = I_{in} \left( \frac{1}{j \omega C_{GD}} + \frac{1}{g_{D}} \right)
\frac{ U_{in}}{I_{in}} = \frac{ \frac{1}{j \omega C_{GD}} + \frac{1}{g_{D}} }{ 1 + \frac{g_{m}}{g_{d}} } = \frac{1}{j \omega C_{GD} \left( 1 + \frac{g_{m}}{g_{d}} \right) } + \frac{1}{ g_{D} \left( 1 + \frac{g_{m}}{g_{d}} \right) }
Drainschaltung, Sourcefollower
Ausgang an der Source
KESB Ersatzschaltbild Eingangswiderstand, Ausgangswiderstand Verstärkung Diese Schaltung wird als Spannungsregler eingesetzt. |
Version 4 SHEET 1 880 680 WIRE 160 0 80 0 WIRE 240 0 160 0 WIRE 80 16 80 0 WIRE 240 32 240 0 WIRE 80 112 80 96 WIRE 160 112 80 112 WIRE 192 112 160 112 WIRE -112 144 -144 144 WIRE -16 144 -32 144 WIRE 80 144 80 112 WIRE 80 144 48 144 WIRE 240 144 240 128 WIRE 240 176 240 144 WIRE 272 176 240 176 WIRE -144 208 -144 144 WIRE 80 224 80 144 WIRE 240 224 240 176 WIRE 240 336 240 304 WIRE -144 352 -144 288 WIRE 80 352 80 304 FLAG 80 352 0 FLAG 240 336 0 FLAG 160 0 VDD IOPIN 160 0 In FLAG -144 352 0 FLAG -144 144 Vin IOPIN -144 144 In FLAG 160 112 VG FLAG 272 176 Vout IOPIN 272 176 Out FLAG 240 144 VS SYMBOL nmos 192 32 R0 SYMATTR InstName M1 SYMATTR Value NMOS1 SYMBOL res 64 208 R0 SYMATTR InstName R2 SYMATTR Value 500k SYMBOL res 64 0 R0 SYMATTR InstName R1 SYMATTR Value 100k SYMBOL res 224 208 R0 WINDOW 3 56 96 VLeft 2 SYMATTR Value 10k SYMATTR InstName R3 SYMBOL cap 48 128 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C3 SYMATTR Value 1� SYMBOL res -16 128 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R7 SYMATTR Value 1k SYMBOL voltage -144 192 R0 WINDOW 123 24 132 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 0 SYMATTR InstName V1 SYMATTR Value SINE(0 0.05 10k) TEXT -224 -128 Left 2 !.model NMOS1 NMOS(LEVEL=1 W=0.1m L=0.1m KP=500u\n+ VT0=1 LAMBDA=0.0167 CGSO=1n CGBO=1n CGDO=200n)\nVDD VDD 0 10 TEXT -232 -8 Left 2 !;tran 0 4m 0 TEXT -232 24 Left 2 !.ac dec 10 1 100MEG |
Drainschaltung Arbeitspunkt
V_{out} = I_{DS} \cdot R_{3} V_{DS} > V_{GS}-V_{Th} SättigungI_{DS} = \beta \left( V_{GS} - V_{Th} \right)^{2} I_{DS} = \beta \left( V_{G} - V_{out} - V_{Th} \right)^{2} V_{out} = \beta \left( V_{G} - V_{out} - V_{Th} \right)^{2} \cdot R_{3} V_{out} = \beta \cdot R_{3} \left( \left( V_{G} - V_{Th} \right)^{2} - 2 \left( V_{G} - V_{Th} \right) V_{out} + V_{out}^{2} \right) V_{out}^{2} - 2 \cdot V_{out} \left( \left( V_{G} - V_{Th} \right) + \frac{1}{2 \cdot \beta \cdot R_{3}} \right) + \left( V_{G} - V_{Th} \right)^{2} = 0
Drainschaltung Arbeitspunkt
\left( V_{out} - \left( V_{G} - V_{Th} \right) - \frac{1}{2 \cdot \beta \cdot R_{3}} \right)^{2} - \left( \left( V_{G} - V_{Th} \right) + \frac{1}{2 \cdot \beta \cdot R_{3}} \right)^{2} + \left( V_{G} - V_{Th} \right)^{2} = 0 \left( V_{out} - \left( V_{G} - V_{Th} \right) - \frac{1}{2 \cdot \beta \cdot R_{3}} \right)^{2} = 2 \frac{V_{G} - V_{Th}}{2 \cdot \beta \cdot R_{3}} + \frac{1}{\left( 2 \cdot \beta \cdot R_{3} \right)^{2} } V_{out} = \left( V_{G} - V_{Th} \right) + \frac{1}{2 \cdot \beta \cdot R_{3}} \pm \sqrt{ \frac{V_{G} - V_{Th}}{ \beta \cdot R_{3}} + \frac{1}{\left( 2 \cdot \beta \cdot R_{3} \right)^{2} }} Positives Vorzeichen kann nicht sein. V_{out} \approx \left( V_{G} - V_{Th} \right)Drainschaltung KESB
Version 4 SHEET 1 880 680 WIRE -80 144 -144 144 WIRE 80 144 0 144 WIRE 176 144 80 144 WIRE 400 144 288 144 WIRE 560 144 400 144 WIRE 656 144 560 144 WIRE 688 144 656 144 WIRE -144 208 -144 144 WIRE 560 208 560 144 WIRE 80 224 80 144 WIRE 176 224 176 144 WIRE 288 224 288 144 WIRE 656 224 656 144 WIRE 80 336 80 304 WIRE 176 336 176 304 WIRE 176 336 80 336 WIRE 288 336 288 304 WIRE 288 336 176 336 WIRE 560 336 560 288 WIRE 560 336 288 336 WIRE 656 336 656 304 WIRE 656 336 560 336 WIRE -144 352 -144 288 WIRE 80 352 80 336 FLAG 80 352 0 FLAG -144 352 0 FLAG -144 144 Vin IOPIN -144 144 In FLAG 176 144 VG FLAG 688 144 Vout IOPIN 688 144 Out FLAG 400 144 VS SYMBOL res 64 208 R0 SYMATTR InstName R2 SYMATTR Value 500k SYMBOL res 160 208 R0 SYMATTR InstName R1 SYMATTR Value 100k SYMBOL res 640 208 R0 WINDOW 3 37 78 Left 2 SYMATTR Value 100 SYMATTR InstName R3 SYMBOL res 16 128 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R7 SYMATTR Value 1k SYMBOL voltage -144 192 R0 WINDOW 123 24 132 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 0 SYMATTR InstName V1 SYMATTR Value SINE(0 0.05 10k) SYMBOL bi 288 224 R0 SYMATTR InstName B1 SYMATTR Value I=- gm*(V(VG)-V(VS)) SYMBOL res 544 192 R0 WINDOW 3 37 78 Left 2 SYMATTR Value 10k SYMATTR InstName RD TEXT -104 360 Left 2 !.tran 0 4m 0 TEXT -112 392 Left 2 !;ac dec 10 1 100MEG TEXT 280 368 Left 2 !.Param gm=100m TEXT 208 120 Left 2 ;VGS LINE Normal 272 144 192 144 LINE Normal 256 128 272 144 LINE Normal 272 144 256 160
|
Verstärkung u_{out} = g_{m} \cdot \left( u_{G} - u_{out} \right) \cdot \left( r_{D} || R_{3} \right) u_{out} \left( 1 + g_{m} \cdot \left( r_{D} || R_{3} \right) \right) = g_{m} \cdot u_{G} \cdot \left( r_{D} || R_{3} \right) \frac{ u_{out}}{u_{G}} = \frac{ g_{m} \cdot \left( r_{D} || R_{3} \right)} { 1 + g_{m} \cdot \left( r_{D} || R_{3} \right) } | \frac{ u_{out}}{u_{G}} = \frac{ 1} { \frac{1}{g_{m} \cdot \left( r_{D} || R_{3} \right)} + 1 } g_{m} \cdot \left( r_{D} || R_{3} \right) >> 1 \frac{ u_{out}}{u_{G}} \approx 1 |
