Elektronik 318 Mehrstufige VerstärkerProf. Dr. Jörg Vollrath17 Differenzverstärker |
Video 18 Endstufen
|
Länge: 1:27:20 |
0:00:20 Versuchsdurchführung Schaltungsaufbau 0:03:22 Verbindungsliste start 0:12:15 Plazierung der Baulemente 0:15:00 Widerstand falsch gesetzt 0:16:32 Erwartungen an Messwerte 0:16:45 Rechnung Verstärkerschaltung 0:18:25 Oszilloskop DC Eingang 0:20:00 Average Gleichanteil, Amplitude Wechselanteil 0:23:07 Der mehrstufige Verstärker 0:25:43 Beispiel 0:26:38 Zerlegung der Schaltung 0:28:43 2.Stufe 0:29:43 Endstufe 0:37:30 Aktive Last 0:43:03 Schaltbild eines Operationsverstärkers TLC272 0:47:16 Ausgangsstufen, A-Betrieb, Sourcefollower 0:50:18 Wirkungsgrad 0:55:43 Klassifizierung Class A 0:58:29 Wirkungsgrad n = 25% 0:59:58 Ausgangssignal 1:06:23 Wirkungsgrad 25%, Simulation in LTSPICE 1:08:43 Class-B Verstärker n = 79% 1:15:44 LTSPICE Simulation 1:18:43 Plateau 1:21:30 AB-Betrieb 1:23:08 Simulation B-Betrieb |
Rückblick und Heute
- Differenzverstärker
- 2 Eingänge, Gleichspannungsverstärkung
- Heute:
- Mehrstufige Verstärkerstufen
- Operationsverstärker
- Ausgangsstufen, Leistung
- Klasse: A
- Klasse: AB
- (Klasse: D)
- Spannungsverstärkung
- Eigenschaften
Mehrstufiger Verstärker Beispiel
|
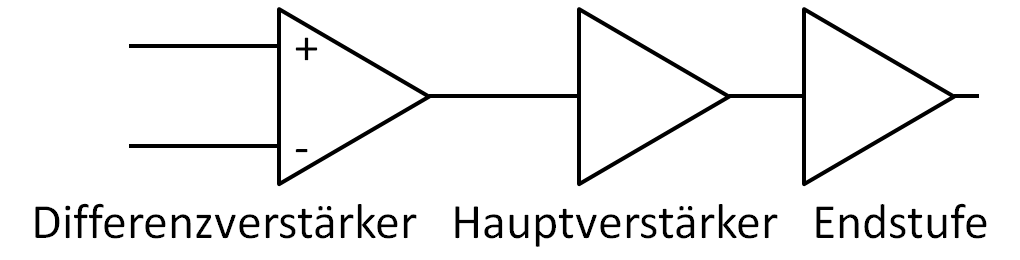
M8: Stromquelle, Strombank 3 Stufen Differenzverstärker: M1, M2,M3, M4 Sourceschaltung: M5, M10 Ausgangsstufe: Typ: AB M6, M7 (Drainschaltung) Transistorgrößen W/L, KN=W/L·KN‘ Eingangswiderstand: \infty Verstärkung v_{d} = v_{u1} \cdot v_{u2} \cdot v_{u3} v_{u3} = 1 |
Version 4 SHEET 1 1356 680 WIRE 416 -32 192 -32 WIRE 512 -32 416 -32 WIRE 592 -32 512 -32 WIRE 656 -32 592 -32 WIRE 864 -32 656 -32 WIRE 912 -32 864 -32 WIRE 1072 -32 912 -32 WIRE 192 -16 192 -32 WIRE 416 -16 416 -32 WIRE 416 -16 368 -16 WIRE 592 -16 592 -32 WIRE 912 16 912 -32 WIRE 912 16 864 16 WIRE 1072 16 1072 -32 WIRE 368 32 368 -16 WIRE 416 32 368 32 WIRE 656 32 656 -32 WIRE 656 32 592 32 WIRE 816 48 800 48 WIRE 496 64 464 64 WIRE 544 64 496 64 WIRE 1104 64 1072 64 WIRE 416 96 416 80 WIRE 496 96 496 64 WIRE 496 96 416 96 WIRE 592 96 592 80 WIRE 672 96 592 96 WIRE 800 96 800 48 WIRE 800 96 672 96 WIRE 864 96 864 64 WIRE 912 96 864 96 WIRE 928 96 912 96 WIRE 1024 96 928 96 WIRE 416 112 416 96 WIRE 592 112 592 96 WIRE 1104 112 1104 64 WIRE 1104 112 1072 112 WIRE 864 144 848 144 WIRE 432 160 416 160 WIRE 592 160 576 160 WIRE 1072 160 1072 112 WIRE 1136 160 1072 160 WIRE 928 176 928 96 WIRE 928 176 912 176 WIRE 368 192 352 192 WIRE 656 192 640 192 WIRE 1072 192 1072 160 WIRE 1136 192 1072 192 WIRE 432 208 432 160 WIRE 432 208 416 208 WIRE 576 208 576 160 WIRE 592 208 576 208 WIRE 848 224 848 144 WIRE 864 224 864 192 WIRE 864 224 848 224 WIRE 912 224 864 224 WIRE 944 224 912 224 WIRE 192 240 192 64 WIRE 208 240 192 240 WIRE 272 240 208 240 WIRE 864 240 864 224 WIRE 1136 240 1136 192 WIRE 1136 240 1072 240 WIRE 208 256 208 240 WIRE 416 256 416 208 WIRE 480 256 416 256 WIRE 512 256 480 256 WIRE 592 256 592 208 WIRE 592 256 512 256 WIRE 944 272 944 224 WIRE 1024 272 944 272 WIRE 880 288 864 288 WIRE 208 304 192 304 WIRE 496 304 480 304 WIRE 816 320 672 320 WIRE 272 336 272 240 WIRE 272 336 256 336 WIRE 368 336 272 336 WIRE 432 336 368 336 WIRE 864 352 864 336 WIRE 880 352 880 288 WIRE 880 352 864 352 WIRE 368 368 368 336 WIRE 672 368 672 320 WIRE 672 368 368 368 WIRE 192 384 192 304 WIRE 208 384 208 352 WIRE 208 384 192 384 WIRE 480 384 480 352 WIRE 480 384 208 384 WIRE 496 384 496 304 WIRE 496 384 480 384 WIRE 864 384 864 352 WIRE 864 384 496 384 WIRE 1072 384 1072 288 WIRE 1072 384 864 384 WIRE 480 400 480 384 FLAG 480 400 0 FLAG 512 -32 VDD IOPIN 512 -32 In FLAG 352 192 VA IOPIN 352 192 In FLAG 656 192 VB IOPIN 656 192 In FLAG 512 256 Vlow FLAG 368 336 Vref FLAG 496 64 OutA FLAG 672 96 OutB FLAG 1136 160 Out IOPIN 1136 160 Out FLAG 912 96 OutC1 FLAG 912 224 OutC2 SYMBOL nmos4 368 112 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M1 SYMATTR Value2 l=1u w=20u SYMBOL pmos4 464 -16 M0 SYMATTR InstName M3 SYMATTR Value CD4007P SYMATTR Value2 l=1u w=50u SYMBOL pmos4 544 -16 R0 WINDOW 3 56 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M4 SYMATTR Value2 l=1u w=50u SYMBOL nmos4 432 256 R0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M9 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 640 112 M0 WINDOW 3 -77 121 Left 2 SYMATTR Value CD4007N SYMATTR InstName M2 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 256 256 M0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M8 SYMATTR Value2 l=1u w=10u SYMBOL current 192 -16 R0 SYMATTR InstName I1 SYMATTR Value 500� SYMBOL pmos4 816 -32 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M5 SYMATTR Value2 l=1u w=99u SYMBOL nmos4 912 96 M0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M11 SYMATTR Value2 l=1u w=5u SYMBOL nmos4 816 240 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M10 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 1024 16 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M6 SYMATTR Value2 l=1u w=10u SYMBOL pmos4 1024 192 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M7 SYMATTR Value2 l=1u w=25u TEXT 160 -160 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u VT0=1.5 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=400u VT0=-1.5 LAMBDA=0.018 CGDO=400n) TEXT 224 416 Left 2 !VB VB 0 5\nVDD VDD 0 10\nV1 VA 0 SINE(5 0.00001 10k) AC 1 TEXT 632 464 Left 2 !.tran 0 0.5m 0 TEXT 632 424 Left 2 !;ac oct 10 1 1MEG TEXT 576 -88 Left 2 ;Mehrstufiger Verstaerker TEXT 128 248 Left 2 ;10\n1 TEXT 408 288 Left 2 ;20\n1 TEXT 344 136 Left 2 ;20\n1 TEXT 640 136 Left 2 ;20\n1 TEXT 464 0 Left 2 ;50\n1 TEXT 520 0 Left 2 ;50\n1 TEXT 792 0 Left 2 ;100\n1 TEXT 1000 48 Left 2 ;10\n1 TEXT 1000 216 Left 2 ;25\n1 TEXT 784 272 Left 2 ;20\n1 TEXT 936 128 Left 2 ;5\n1 LINE Normal 288 384 288 384 LINE Normal 288 384 288 384 LINE Normal 288 400 288 400 LINE Normal 288 400 288 400 LINE Normal 752 -64 752 -64 LINE Normal 736 400 736 -48 1 LINE Normal 976 400 976 -48 1 LINE Normal 288 400 288 -48 1  |
Mehrstufiger Verstärker Beispiel
Version 4 SHEET 1 1396 680 WIRE 416 -32 192 -32 WIRE 512 -32 416 -32 WIRE 592 -32 512 -32 WIRE 656 -32 592 -32 WIRE 864 -32 656 -32 WIRE 912 -32 864 -32 WIRE 1072 -32 912 -32 WIRE 192 -16 192 -32 WIRE 416 -16 416 -32 WIRE 416 -16 368 -16 WIRE 592 -16 592 -32 WIRE 912 16 912 -32 WIRE 912 16 864 16 WIRE 1072 16 1072 -32 WIRE 368 32 368 -16 WIRE 416 32 368 32 WIRE 656 32 656 -32 WIRE 656 32 592 32 WIRE 816 48 800 48 WIRE 496 64 464 64 WIRE 544 64 496 64 WIRE 1104 64 1072 64 WIRE 416 96 416 80 WIRE 496 96 496 64 WIRE 496 96 416 96 WIRE 592 96 592 80 WIRE 672 96 592 96 WIRE 800 96 800 48 WIRE 800 96 672 96 WIRE 864 96 864 64 WIRE 912 96 864 96 WIRE 928 96 912 96 WIRE 1024 96 928 96 WIRE 416 112 416 96 WIRE 592 112 592 96 WIRE 1104 112 1104 64 WIRE 1104 112 1072 112 WIRE 864 144 848 144 WIRE 432 160 416 160 WIRE 592 160 576 160 WIRE 1072 160 1072 112 WIRE 1200 160 1072 160 WIRE 1216 160 1200 160 WIRE 928 176 928 96 WIRE 928 176 912 176 WIRE 368 192 336 192 WIRE 656 192 640 192 WIRE 1072 192 1072 160 WIRE 1136 192 1072 192 WIRE 432 208 432 160 WIRE 432 208 416 208 WIRE 576 208 576 160 WIRE 592 208 576 208 WIRE 848 224 848 144 WIRE 864 224 864 192 WIRE 864 224 848 224 WIRE 912 224 864 224 WIRE 944 224 912 224 WIRE 192 240 192 64 WIRE 208 240 192 240 WIRE 272 240 208 240 WIRE 864 240 864 224 WIRE 1136 240 1136 192 WIRE 1136 240 1072 240 WIRE 208 256 208 240 WIRE 416 256 416 208 WIRE 480 256 416 256 WIRE 512 256 480 256 WIRE 592 256 592 208 WIRE 592 256 512 256 WIRE 944 272 944 224 WIRE 1024 272 944 272 WIRE 1200 272 1200 160 WIRE 880 288 864 288 WIRE 208 304 192 304 WIRE 496 304 480 304 WIRE 816 320 672 320 WIRE 272 336 272 240 WIRE 272 336 256 336 WIRE 368 336 272 336 WIRE 432 336 368 336 WIRE 864 352 864 336 WIRE 880 352 880 288 WIRE 880 352 864 352 WIRE 368 368 368 336 WIRE 672 368 672 320 WIRE 672 368 368 368 WIRE 1200 368 1200 352 WIRE 192 384 192 304 WIRE 208 384 208 352 WIRE 208 384 192 384 WIRE 480 384 480 352 WIRE 480 384 208 384 WIRE 496 384 496 304 WIRE 496 384 480 384 WIRE 864 384 864 352 WIRE 864 384 496 384 WIRE 1072 384 1072 288 WIRE 1072 384 864 384 WIRE 480 400 480 384 FLAG 480 400 0 FLAG 512 -32 VDD IOPIN 512 -32 In FLAG 336 192 VA IOPIN 336 192 In FLAG 656 192 VB IOPIN 656 192 In FLAG 512 256 Vlow FLAG 368 336 Vref FLAG 496 64 OutA FLAG 672 96 OutB FLAG 1216 160 Out IOPIN 1216 160 Out FLAG 912 96 OutC1 FLAG 912 224 OutC2 FLAG 1200 368 Vmid SYMBOL nmos4 368 112 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M1 SYMATTR Value2 l=1u w=20u SYMBOL pmos4 464 -16 M0 SYMATTR InstName M3 SYMATTR Value CD4007P SYMATTR Value2 l=1u w=50u SYMBOL pmos4 544 -16 R0 WINDOW 3 56 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M4 SYMATTR Value2 l=1u w=50u SYMBOL nmos4 432 256 R0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M9 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 640 112 M0 WINDOW 3 -77 121 Left 2 SYMATTR Value CD4007N SYMATTR InstName M2 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 256 256 M0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M8 SYMATTR Value2 l=1u w=10u SYMBOL current 192 -16 R0 SYMATTR InstName I1 SYMATTR Value 500� SYMBOL pmos4 816 -32 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M5 SYMATTR Value2 l=1u w=99u SYMBOL nmos4 912 96 M0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M11 SYMATTR Value2 l=10u w=1u SYMBOL nmos4 816 240 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M10 SYMATTR Value2 l=1u w=20u SYMBOL nmos4 1024 16 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M6 SYMATTR Value2 l=1u w=10u SYMBOL pmos4 1024 192 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M7 SYMATTR Value2 l=1u w=25u SYMBOL res 1184 256 R0 SYMATTR InstName R1 SYMATTR Value 100 TEXT 160 -160 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u VT0=1.5 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=400u VT0=-1.5 LAMBDA=0.018 CGDO=400n) TEXT 224 416 Left 2 !VB VB 0 5\nVDD VDD 0 10\nVMID VMID 0 DC 5\nV1 VA 0 SINE(5 0.00002 10k) AC 1 TEXT 632 464 Left 2 !.tran 0 0.5m 0 TEXT 632 424 Left 2 !;ac oct 10 1 1MEG TEXT 576 -88 Left 2 ;Mehrstufiger Verstaerker TEXT 128 248 Left 2 ;10\n1 TEXT 408 288 Left 2 ;20\n1 TEXT 344 136 Left 2 ;20\n1 TEXT 640 136 Left 2 ;20\n1 TEXT 464 0 Left 2 ;50\n1 TEXT 520 0 Left 2 ;50\n1 TEXT 768 0 Left 2 ;100\n1 TEXT 1000 48 Left 2 ;10\n1 TEXT 1000 216 Left 2 ;25\n1 TEXT 784 272 Left 2 ;20\n1 TEXT 936 128 Left 2 ;1\n10 LINE Normal 288 384 288 384 LINE Normal 288 384 288 384 LINE Normal 288 400 288 400 LINE Normal 288 400 288 400 LINE Normal 752 -64 752 -64 LINE Normal 736 400 736 -48 1 LINE Normal 976 400 976 -48 1 LINE Normal 288 400 288 -48 1
|
VDD = 10 V, I1 = 500 µA,
Kpn' = 1 mAV-2,
Kpp' = 400 µAV-2,
VThn = 1.5 V, VThp = -1.5 V,
λ = 0.018 V-1 Bestimmen Sie die Gegentaktspannungsverstärkung. Im Schaltbild sind an den Transistoren die Weiten und Längen angegeben. M2 hat ein W/L-Verhältnis von 20/1. Kpn' und Kpp' müssen mit diesem Verhältnis multipliziert werden.
Arbeitspunkt: g_m, r_o
Spannungsverstärkung v_{D} = - g_{M2} \cdot \left( r_{DS2} || r_{DS4} \right) v_{u2} = - g_{M5} \cdot \left( r_{DS5} || \left( r_{DS10} + \frac{1}{g_{m11}} \right) \right)
Ausgangswiderstand
Drainschaltung R_o = \frac{1}{g_{m6}+g_{m7}} Für gm benötigt man den Strom IDS bzw. die Spannung UGS V_{GS6} = \frac{1}{2} V_{GS11} = \frac{1}{2} V_{DS11} V_{GS11} = V_{Thn} + \sqrt{\frac{2 I_{DS11}}{K_{pp11}^{'} \cdot \frac{W}{L}}} = 1.5 V + \sqrt{\frac{2 \cdot 200 \mu A \cdot 10}{1 mA}} = 1.5 V + 0.63 V = 3.5 V
g_{m} = \frac{2 \cdot I_{DS}}{V_{GS} - V_{Thn}}
= \frac{2 \cdot I_{DS}}{\sqrt{\frac{2 \cdot I_{DS} \cdot L}{K_{pn}^{'} \cdot W}}}
= \sqrt{2 \cdot \frac{W}{L} \cdot K_{pn}^{'} \cdot I_{DS}}
r_{DS}= \frac{1}{\lambda \cdot I_{DS}}
g_{m2} = \sqrt{2 \cdot 20 \cdot 1 mAV^{-2} \cdot 0.5 mA} = 4.47 mS
r_{DS2} = r_{DS4} = \frac{1}{0.018V^{-1} \cdot 0.5 mA} = 111 k \Omega v_{D} = - 4.47 mS \cdot 55.5 k \Omega = - 248 r_{DS5} = r_{DS11} = r_{DS10} = \frac{1}{0.018V^{-1} \cdot 1 mA} = 56 k \Omega g_{m5} = \sqrt{2 \cdot 100 \cdot 400 \mu AV^{-2} \cdot 1 mA} = 8.9 mS g_{m11} = \sqrt{2 \cdot \frac{1}{10} \cdot 1000 \mu AV^{-2} \cdot 1 mA} = 0.45 mS r_{m11} = 2236 \Omega r = r_{DS5} || ( r_{m11} + r_{DS10} ) = 28.3 k \Omega v_{u2} = - 8.9 mS \cdot 28.3 k \Omega = - 252 v = v_{D} \cdot v_{u2} = 248 \cdot 252 = 62574 A_v = 20 log( 62574) dB = 95.9 dB |
Ausgangsstufen, Leistungsendstufen A-Betrieb
|
Version 4 SHEET 1 1356 680 WIRE 496 64 208 64 WIRE 496 80 496 64 WIRE 512 128 496 128 WIRE 448 160 304 160 WIRE 208 192 208 64 WIRE 304 192 304 160 WIRE 496 208 496 176 WIRE 512 208 512 128 WIRE 512 208 496 208 WIRE 640 208 512 208 WIRE 656 208 640 208 WIRE 640 224 640 208 WIRE 512 240 512 208 WIRE 208 320 208 272 WIRE 304 320 304 272 WIRE 640 320 640 304 WIRE 512 336 512 320 WIRE 512 336 480 336 FLAG 496 64 VDD FLAG 304 320 0 FLAG 656 208 OUT2 IOPIN 656 208 Out FLAG 640 320 0 FLAG 208 320 0 FLAG 480 336 VSS SYMBOL voltage 304 176 R0 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V1 SYMATTR Value SINE(0 10 5k) SYMBOL nmos4 448 80 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M1 SYMATTR Value2 l=1u w=10000u SYMBOL res 624 208 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL voltage 208 176 R0 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V2 SYMATTR Value 10 SYMBOL current 512 240 R0 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName I1 SYMATTR Value 100m TEXT 592 80 Left 2 !.tran 0 1m 0 TEXT 408 112 Left 2 ;10\n1 TEXT 192 -16 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u\n+ VT0=0.0 LAMBDA=0.018 CGDO=400n) TEXT 184 40 Left 2 !VSS VSS 0 -10 |
Man spricht von A-Betrieb, wenn die Ausgangsspannung vom Transistor
nur in eine Richtung verändert werden kann (pull).
Ausgangsstufen, Leistungsendstufen A-Betrieb
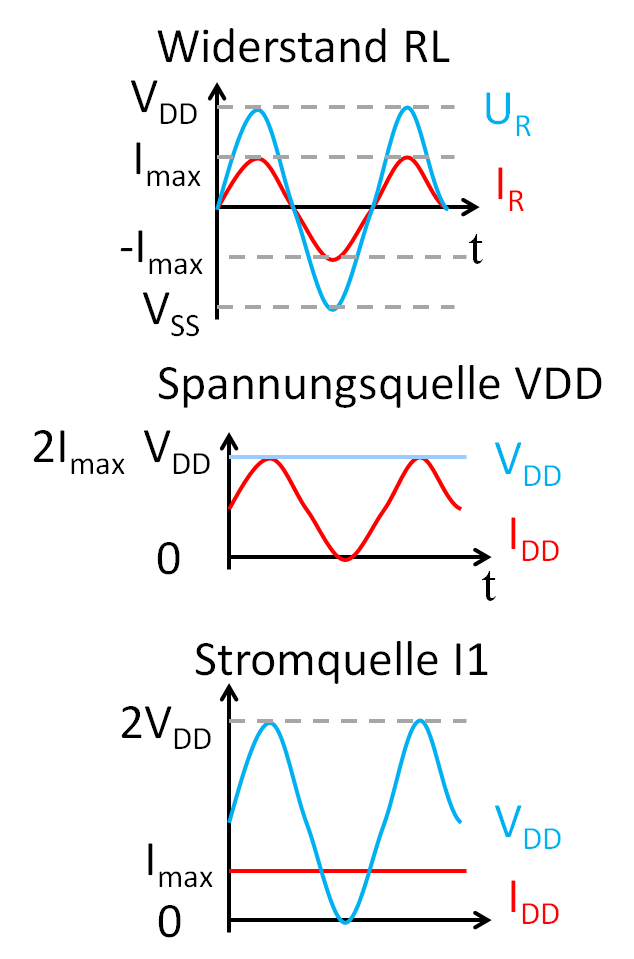
Leistung am WiderstandP_{RL} = \frac{V_{DD} \cdot I_{max}}{2} Leistung an der Spannungsquelle VDDP_{VDD} = \frac{1}{T} \int_0^{T} \left( V_{DD} \cdot \left( I_{max} + I_{max} \cdot sin( \omega t ) \right) \right) dt P_{VDD} = V_{DD} \cdot I_{max} Leistung an der Stromquelle I1P_{I1} = \frac{1}{T} \int_0^{T} \left( \left( V_{DD} + V_{DD} \cdot sin( \omega t ) \right) \cdot I_{1} \right) dt P_{VDD} = V_{DD} \cdot I_{max} Wirkungsgrad\eta = \frac{P_{RL}}{ P_{I1} + P_{VDD}} = \frac{\frac{V_{DD} \cdot I_{max}}{2}}{V_{DD} \cdot I_{max} + V_{DD} \cdot I_{max}} = \frac{1}{4} = 25 \% |
|
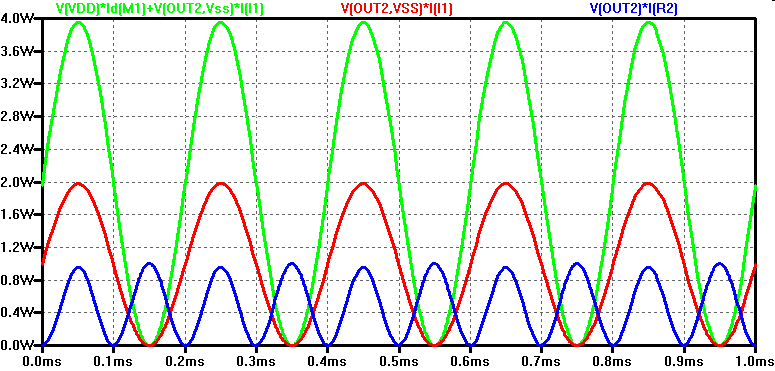
Ausgangsstufen, Leistungsendstufen A-Betrieb
|
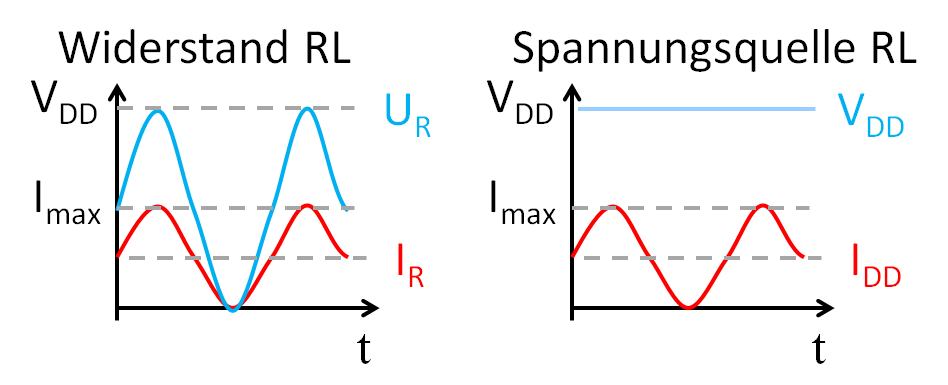
Wechselsignalleistung an R P_{R \sim} = \frac{\frac{V_{DD}}{2} \cdot \frac{I_{max}}{2}}{2} = \frac{V_{DD} \cdot I_{max}}{8} Amplituden VDD/2 und Imax/2, Wechselspannung \sqrt{2} Gesamtleistung P_{G} = \frac{1}{T} \int_0^{T} V_{DD} \cdot (\frac{I_{max}}{2} + \frac{I_{max}}{2} sin(\omega t) ) dt P_{G} = \frac{VDD \cdot Imax}{2} Wirkungsgrad \eta = \frac{P_{R \sim}}{P_{G}} = \frac{2}{8} = 0.25\% |
Version 4 SHEET 1 1356 680 WIRE 496 64 208 64 WIRE 496 80 496 64 WIRE 512 128 496 128 WIRE 448 160 304 160 WIRE 208 192 208 64 WIRE 304 192 304 160 WIRE 496 208 496 176 WIRE 512 208 512 128 WIRE 512 208 496 208 WIRE 512 224 512 208 WIRE 528 224 512 224 WIRE 512 240 512 224 WIRE 208 320 208 272 WIRE 304 320 304 272 WIRE 512 336 512 320 FLAG 496 64 VDD FLAG 304 320 0 FLAG 528 224 OUT2 IOPIN 528 224 Out FLAG 512 336 0 FLAG 208 320 0 SYMBOL voltage 304 176 R0 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V1 SYMATTR Value SINE(5 5 5k) SYMBOL nmos4 448 80 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M1 SYMATTR Value2 l=1u w=10000u SYMBOL res 496 224 R0 SYMATTR InstName RL SYMATTR Value 100 SYMBOL voltage 208 176 R0 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V2 SYMATTR Value 10 TEXT 592 80 Left 2 !.tran 0 1m 0 TEXT 408 112 Left 2 ;10\n1 TEXT 192 -16 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u\n+ VT0=0.0 LAMBDA=0.018 CGDO=400n) 
|
Ausgangsstufen, Leistungsendstufen B-Betrieb
P_{VDD} = \frac{1}{T} \int_0^{T/2} V_{DD} \frac{V_{DD}}{R_{L}} sin( \frac{2 \pi}{T} t) dt P_{VDD} = \frac{1}{T} [ - \frac{V_{DD}^2 T}{2 \pi \cdot R_{L}} cos( \frac{2 \pi}{T} t)]_{0}^{T/2} P_{VDD} = \frac{1}{T} \frac{V_{DD}^2}{R_{L}} \frac{T}{\pi} = \frac{V_{DD}^2}{\pi R_{L}} P_{VDD} = P_{VSS} P_{G} = P_{VSS} + P_{VDD} = \frac{2 \cdot V_{DD}^2}{\pi R_{L}} \eta = \frac{P_{\sin}}{P_{G}} = \frac{\frac{V_{DD}^{2}}{2 \cdot R_{L}}}{\frac{2 \cdot V_{DD}^2}{\pi R_{L}}} = \frac{\pi}{4} = 0.79 = 79 \% |
Version 4 SHEET 1 1808 680 WIRE 912 0 864 0 WIRE 1040 0 912 0 WIRE 1072 0 1040 0 WIRE 1072 16 1072 0 WIRE 912 48 912 0 WIRE 912 48 864 48 WIRE 1104 64 1072 64 WIRE 816 80 768 80 WIRE 1024 96 944 96 WIRE 1104 112 1104 64 WIRE 1104 112 1072 112 WIRE 1072 128 1072 112 WIRE 1200 128 1072 128 WIRE 1216 128 1200 128 WIRE 864 144 864 96 WIRE 944 144 944 96 WIRE 944 144 864 144 WIRE 1072 160 1072 128 WIRE 1136 160 1072 160 WIRE 864 176 864 144 WIRE 1200 192 1200 128 WIRE 1136 208 1136 160 WIRE 1136 208 1072 208 WIRE 944 240 944 144 WIRE 1024 240 944 240 WIRE 1200 288 1200 272 WIRE 864 304 864 256 WIRE 1024 304 864 304 WIRE 1072 304 1072 256 WIRE 1072 304 1024 304 FLAG 1040 0 VDD FLAG 1216 128 Out IOPIN 1216 128 Out FLAG 864 144 OutC1 FLAG 768 80 VA IOPIN 768 80 In FLAG 1200 288 0 FLAG 1024 304 VSS SYMBOL current 864 176 R0 SYMATTR InstName I1 SYMATTR Value 1m SYMBOL pmos4 816 0 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M5 SYMATTR Value2 l=1u w=99u SYMBOL nmos4 1024 16 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M6 SYMATTR Value2 l=1u w=150u SYMBOL pmos4 1024 160 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M7 SYMATTR Value2 l=1u w=250u SYMBOL res 1184 176 R0 SYMATTR InstName RL SYMATTR Value 100 TEXT 744 -168 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u \n+ VT0=0.5 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=400u \n+ VT0=-0.5 LAMBDA=0.018 CGDO=400n) TEXT 744 336 Left 2 !VDD VDD 0 5\nVSS VSS 0 -5\nV1 VA 0 SINE(4.284 0.008 10k) AC 1 TEXT 1072 344 Left 2 !.tran 0 0.5m 0 TEXT 832 -48 Left 2 ;Class B Verstaerker TEXT 792 32 Left 2 ;100\n1 TEXT 1000 48 Left 2 ;10\n1 TEXT 1000 184 Left 2 ;25\n1 LINE Normal 976 320 976 -16 1 |
Ausgangsstufen, Leistungsendstufen AB-Betrieb
|
Version 4 SHEET 1 1808 680 WIRE 912 -32 864 -32 WIRE 1072 -32 912 -32 WIRE 912 16 912 -32 WIRE 912 16 864 16 WIRE 1072 16 1072 -32 WIRE 816 48 800 48 WIRE 1104 64 1072 64 WIRE 800 96 800 48 WIRE 800 96 752 96 WIRE 864 96 864 64 WIRE 912 96 864 96 WIRE 928 96 912 96 WIRE 1024 96 928 96 WIRE 1104 112 1104 64 WIRE 1104 112 1072 112 WIRE 864 144 848 144 WIRE 1072 160 1072 112 WIRE 1200 160 1072 160 WIRE 1216 160 1200 160 WIRE 928 176 928 96 WIRE 928 176 912 176 WIRE 1072 192 1072 160 WIRE 1136 192 1072 192 WIRE 848 224 848 144 WIRE 864 224 864 192 WIRE 864 224 848 224 WIRE 912 224 864 224 WIRE 944 224 912 224 WIRE 1200 224 1200 160 WIRE 1136 240 1136 192 WIRE 1136 240 1072 240 WIRE 864 256 864 224 WIRE 944 272 944 224 WIRE 1024 272 944 272 WIRE 1200 320 1200 304 WIRE 864 384 864 336 WIRE 1008 384 864 384 WIRE 1072 384 1072 288 WIRE 1072 384 1008 384 FLAG 1072 -32 VDD IOPIN 1072 -32 In FLAG 1216 160 Out IOPIN 1216 160 Out FLAG 912 96 OutC1 FLAG 912 224 OutC2 FLAG 752 96 VA FLAG 1008 384 VSS FLAG 1200 320 0 SYMBOL current 864 256 R0 SYMATTR InstName I1 SYMATTR Value 1m SYMBOL pmos4 816 -32 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M5 SYMATTR Value2 l=1u w=99u SYMBOL nmos4 912 96 M0 WINDOW 3 77 58 Left 2 SYMATTR Value CD4007N SYMATTR InstName M11 SYMATTR Value2 l=10u w=1u SYMBOL nmos4 1024 16 R0 WINDOW 3 83 72 Left 2 SYMATTR Value CD4007N SYMATTR InstName M6 SYMATTR Value2 l=1u w=10u SYMBOL pmos4 1024 192 R0 WINDOW 3 59 73 Left 2 SYMATTR Value CD4007P SYMATTR InstName M7 SYMATTR Value2 l=1u w=25u SYMBOL res 1184 208 R0 SYMATTR InstName R1 SYMATTR Value 1000 TEXT 744 -184 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1000u \n+ VT0=1.5 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=400u \n+ VT0=-1.5 LAMBDA=0.018 CGDO=400n) TEXT 696 368 Left 2 !VDD VDD 0 5\nVSS VSS 0 -5\nV1 VA 0 SINE(3.282 0.005 10k) AC 1 TEXT 1096 368 Left 2 !.tran 0 0.5m 0 TEXT 784 -64 Left 2 ;Class AB Verstaerker TEXT 768 0 Left 2 ;100\n1 TEXT 1000 48 Left 2 ;10\n1 TEXT 1000 216 Left 2 ;25\n1 TEXT 936 128 Left 2 ;1\n10 TEXT 1096 400 Left 2 !;ac dec 10 1 1G LINE Normal 976 400 976 -48 1 |
H-Bridge und D-Betrieb
- Der D-Betrieb mit H- Brücke
- Digitales Pulsweitenmoduliertes Eingangssignal
Tiefpass erzeugt ein Sinussignal
DA Wandler
H Brücke: Rechts und Links sind Inverter und in der Mitte die Last.
Die Last sieht die doppelte Versorgungsspannung.
Version 4 SHEET 1 880 680 WIRE 240 16 80 16 WIRE 416 16 240 16 WIRE 80 32 80 16 WIRE 112 32 80 32 WIRE 416 32 416 16 WIRE 416 32 384 32 WIRE 32 48 16 48 WIRE 496 48 464 48 WIRE 112 80 112 32 WIRE 112 80 80 80 WIRE 384 80 384 32 WIRE 416 80 384 80 WIRE -48 96 -144 96 WIRE 16 96 16 48 WIRE 16 96 -48 96 WIRE -144 128 -144 96 WIRE -144 128 -160 128 WIRE -48 128 -112 128 WIRE 16 128 -48 128 WIRE 208 128 208 80 WIRE 208 128 80 128 WIRE 288 128 288 80 WIRE 416 128 288 128 WIRE 80 144 80 128 WIRE 208 144 208 128 WIRE 288 144 288 128 WIRE 416 144 416 128 WIRE -272 160 -320 160 WIRE -112 160 -112 128 WIRE -112 160 -160 160 WIRE -272 192 -320 192 WIRE -112 192 -160 192 WIRE 112 192 80 192 WIRE 416 192 384 192 WIRE 256 208 208 208 WIRE 288 208 256 208 WIRE -144 224 -160 224 WIRE -112 224 -112 192 WIRE -48 224 -112 224 WIRE 0 224 -48 224 WIRE 16 224 16 128 WIRE 32 224 16 224 WIRE 256 224 256 208 WIRE 480 224 464 224 WIRE 112 240 112 192 WIRE 112 240 80 240 WIRE 384 240 384 192 WIRE 416 240 384 240 WIRE -144 256 -144 224 WIRE -48 256 -144 256 WIRE -16 256 -48 256 WIRE 80 272 80 240 WIRE 240 272 80 272 WIRE 416 272 416 240 WIRE 416 272 240 272 WIRE 240 304 240 272 WIRE 0 336 0 224 WIRE 496 336 496 48 WIRE 496 336 0 336 WIRE -16 368 -16 256 WIRE 480 368 480 224 WIRE 480 368 -16 368 FLAG 240 16 VDD IOPIN 240 16 In FLAG 256 224 0 FLAG 240 304 0 FLAG 208 80 Vp FLAG 288 80 Vn FLAG -320 192 Vp FLAG -320 160 Vn FLAG -48 96 LO FLAG -48 128 LU FLAG -48 224 RO FLAG -48 256 RU SYMBOL cap 192 144 R0 WINDOW 0 -37 43 Left 2 WINDOW 3 -37 71 Left 2 SYMATTR InstName C1 SYMATTR Value 200n SYMBOL cap 272 144 R0 WINDOW 0 42 44 Left 2 WINDOW 3 42 72 Left 2 SYMATTR InstName C2 SYMATTR Value 200n SYMBOL nmos4 32 144 R0 SYMATTR InstName M1N SYMATTR Value N SYMATTR Value2 l=0.5u w=1m SYMBOL nmos4 464 144 M0 SYMATTR InstName M2N SYMATTR Value N SYMATTR Value2 l=0.5u w=1m SYMBOL pmos4 464 128 R180 SYMATTR InstName M3P SYMATTR Value P SYMATTR Value2 l=0.5u w=2m SYMBOL pmos4 32 128 M180 SYMATTR InstName M4 SYMATTR Value P SYMATTR Value2 l=0.5u w=2m SYMBOL res 304 112 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL ClassD_Regelung -224 176 R0 SYMATTR InstName X1 TEXT -336 352 Left 2 !.tran 0 1150u 350u 50u uic TEXT -352 288 Left 2 !.options plotwinsize=0\n.include cmosedu_models.txt TEXT -320 32 Left 2 !VDD VDD 0 DC 1 TEXT -312 0 Left 2 !V1 V1 0 SINE(0 0.85 5k) AC 1
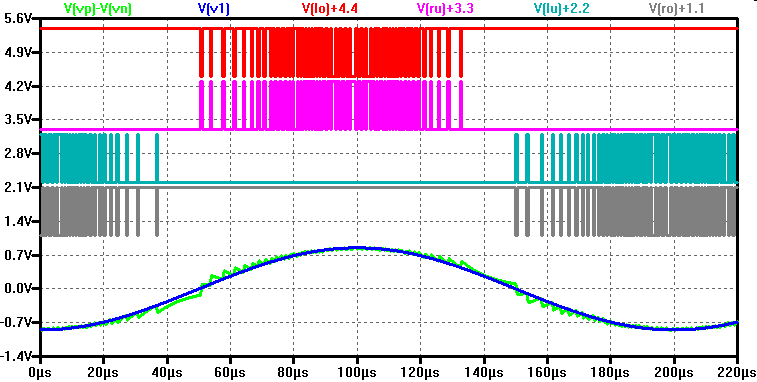Bei der Simulation wird mit dieser Dimensionierung nur ein Wirkungsgrad von 75 % erreicht, da der Lastwiderstand 100 Ω und der Transistorwiderstand bei 20 Ω liegt.
Man muss die Schaltfrequenz, den Transistorwiderstand, den Lastwiderstand und die Kapazitäten für eine gewisse Bandbreite optimieren.
Zusammenfassung
- Mehrstufiger Verstärker
- Zerlegung einer komplexen Schaltung in Teilschaltungen
- Referenzstrom, Differenzverstärker, Sourceschaltung, Ausgangsstufe
- Ausgangsstufen, Leistung
- Klasse: A, AB, D
- Wirkungsgrad, Ausgangswiderstand
Nächstes Mal:
19 Operationsverstärker