Elektronik 3

19 Operationsverstärker

Prof. Dr. Jörg Vollrath

18 Mehrstufiger Verstärker

Video 19 Operationsverstärker 7.12.2020

Länge: 1:27:20

0:0:7 Operationsverstärker

0:0:59 CMOS Operationsverstärker TLC272

0:3:4 Gebondeter Chip TLC272

0:6:13 Schaltsymbol

0:9:16 Kennlinie des Operationsverstärkers Differenzverstärkung

0:14:17 Offsetspannung

0:17:35 Gleichtaktverstärkung

0:21:2 Ersatzschaltbild

0:22:7 LTSPICE Modell

0:28:12 Realer Operationsverstärker 741 versus TLC272

0:32:13 Slew rate

0:36:3 Sinusfunktion und slew rate

0:41:53 Versuch 9

0:43:33 Frequenzgang

0:47:33 Übertragungsfunktion R C

0:49:37 Komplexe Stromgleichung

0:53:37 Bodediagramm Maß über der Frequenz

0:55:32 20 log|1/C1/R1|

0:57:31 ω gegen &infty; 20 log|1/(jw)|

1:0:17 f3dB Eckfrequenz, Grenzfrequenz

1:3:5 Erklärung 3dB Eckfrequenz

1:8:54 LTSPICE Simulation

1:11:34 Frequenzgang Operationsverstärker

Rückblick und Heute

Schaltsymbol, Übertragungskennlinie
Idealer Operationsverstärker
Realer Operationsverstärker
Dynamisches Verhalten, Kompensation
Verstärkerschaltungen mit Operationsverstärkern

Reinhold Kap. 8, S.132-140, Kap. 12 S.227-
Jaeger: Chap. 10 S.529-,

Operationsverstärker

Beispielrechnung: Mehrstufiger Verstärker
Operationsverstärker

Schaltbild
ideales Verhalten: $U_{D} = 0, v_u = \infty , U_{A} endlich$
Frequenzverhalten
Slew Rate
Typische Daten

CMOS Operationsverstärker TLC272

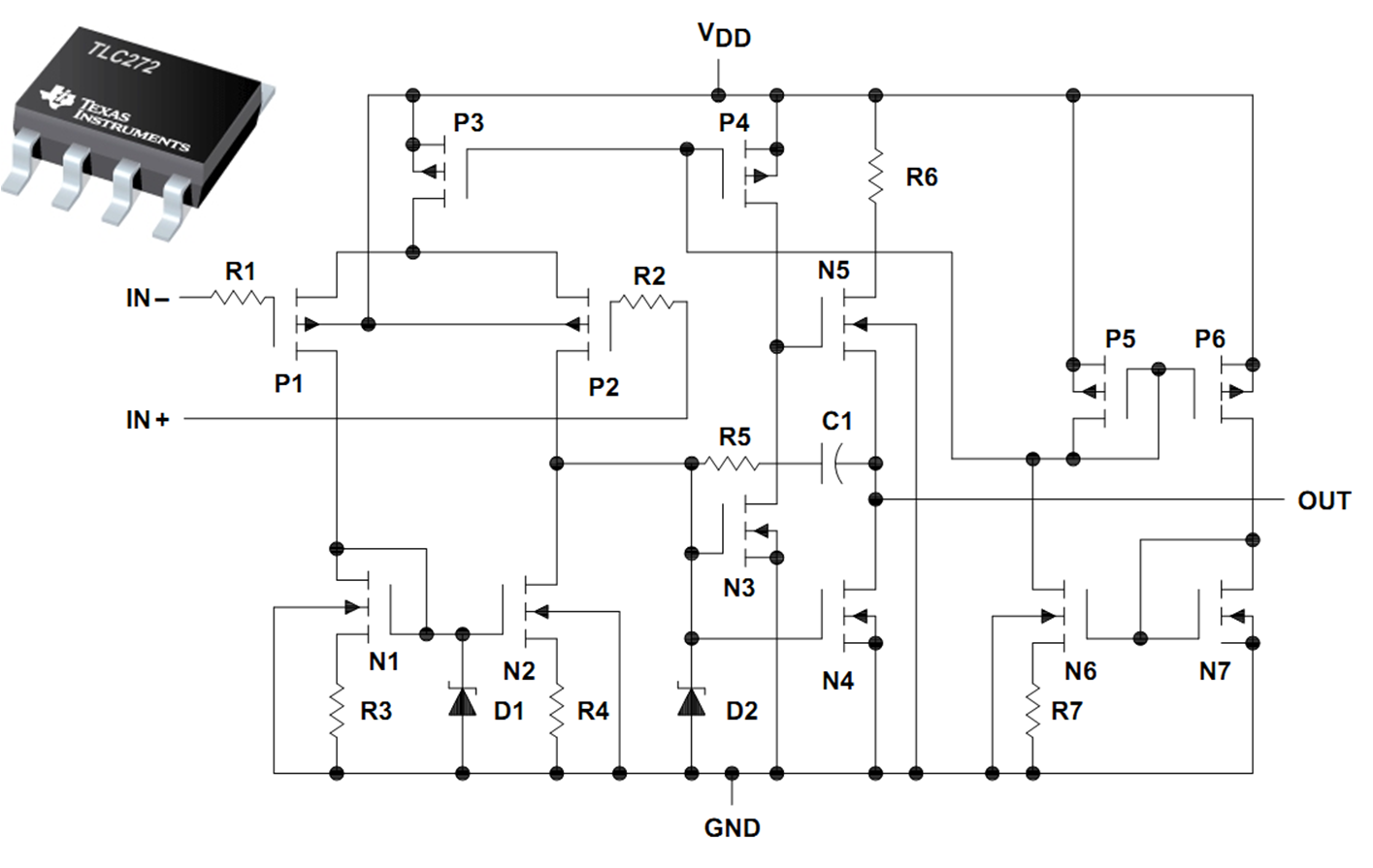
Quelle: Texas Instruments Datenblatt tlc272a.pdf

Referenzstromquelle rechts: P5, P6, N6, N7, R7
Differenzverstärker: P1, P2, P3, N1, N2
Zenerdiode für den Startup
2.te Verstärkerstufe: Sourceschaltung: N3, P4
Ausgangsstufe: N4, N5
Frequenzgangkompensation: R5, C1

CMOS Operationsverstärker TLC272 gebondeter Chip

Man kann integrierte Bauelemente auch als Wafer oder Chips bekommen.
Das Bild zeigt den Chip TLC272 dessen Bondpads mit feinen Golddrähten (25 µm Dicke) mit dem Gehäuse verbunden sind.
Pin 1 ist bei dem Bild rechts oben, damit die Eingänge links und die Ausgänge rechts sind.
Die Chips wurden hier an der Hochschule Kempten im Labor Mikrosystemtechnik gebondet.
Es befinden sich 2 Operationsverstäker auf dem Chip. Einer oben und einer unten.
Die Spannungsversorgungspads befinden sich in der Mitte rechts (VDD) und links (GND).
Links oben und unten befinden sich jeweils die beiden Eingänge.
Links In+ rechts In-.
Rechts oben und unten befinden sich die Ausgänge.
Der Chip ist 1.524 mm x 1.8542 mm (60 mil x 73 mil) gross.
Weitere Informationen findet man auch im Datenblatt.

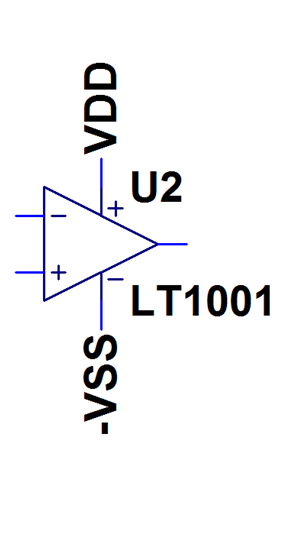
Operationsverstärker: Schaltsymbol

Spannungsgesteuerte Spannungsquelle
2 Eingänge

Nichtinvertierend +
Invertierend –
$U_{a} = v_{UD} \cdot \left( U_{P} - U_{N} \right)$
$v_{UD}$ : Spannungsverstärkung

Versorgung: symmetrisch zum Massepotential

Positive und negative Betriebsspannung

Ideale Eigenschaften
Die Wirkung in einer Schaltung wird durch externe Bauelemente bestimmt: Gegenkopplung

DIN Symbol Wikipedia

Operationsverstärker: Eigenschaften und Übertragungskennlinie

Ausschließlich Differenzverstärkung

U_a = v_UD · U_D

Unendlich große Verstärkung

$v_{UD} \rightarrow \infty$

Kein Eingangsstrom: I₊ = I_- = 0
Unendlich hoher Eingangswiderstand

$r_{e} \rightarrow \infty$

Vernachlässigbarer Ausgangswiderstand $r_{a} = 0$
Kein Offset U_a(U_D = 0) = 0
U_OS = U_D ( U_a = 0 )
Spiegelsymmetrische Übertragungskennlinie
Frequenzunabhängiges Übertragungsverhalten

Es gibt beim Operationsverstärker einen positiven und einen negativen Eingang.
Der Operationsverstärker benötigt eine Spannungsversorgung mit positiver (UB+) und negativer (UB-) Spannung.
Die dargestellte Übertragungskennlinie zeigt eine ideale Kurve und einen Operationsverstärker mit Offset. Diese Kennlinie ist in diesem Fall nach rechts verschoben.
Die maximal erreichbaren Spannungen am Ausgang werden durch die Betriebsspannung begrenzt.
Ein Operationsverstärker hat eine sehr grosse Verstärkung. Die x-Achse stellt deshalb die Eingangsdifferenzspannung im Millivoltbereich dar, während die y-Achse die Ausgangsspannung im Voltbereich zeigt.

Gleichtakteingangsspannung

Common mode rejection rate (CMRR)
Angabe in Dezibel
$CMRR = 20 log G = 20log\frac{v_{UD}}{v_{Gl}}$
Der Gleichtaktaussteuerbereich ist kleiner als die Versorgungsspannung

DC Gleichtakt Übertragungskennlinie Ua = f(UGL)

Ersatzschaltbild

Idealer Operationsverstärker
$U_D = U_{+} - U_{-}$

Realer Operationsverstärker

Offset Spannung

$U_{OS}$

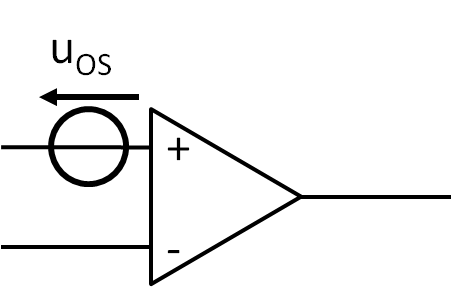Ersatzschaltbild OP mit

$U_{os}$

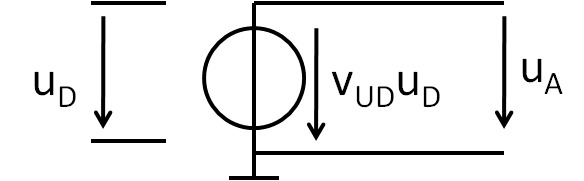LTSPICE Modell

Eingänge: InP (positiv), InM (negativ, Minus)
Ausgang: Out
Spannungsgesteuerte Stromquelle: G1

Leerlaufverstärkung: VDol (open loop)
.PARAM VDol 100k

Ausgangswiderstand und Transitfrequenz: R1, C1

Gainbandwith: GBW
.PARAM GBW 1E6
Transitfrequez: 1 MHz

Begrenzung der Ausgangsspannung

Dioden: D1, D2
Diodenmodell: LIMITV mit einem sehr kleinen Rs
Spannungsquellen: V3, V4

OpAmpModel.asc

Version 4
SHEET 1 880 680
WIRE 128 -128 128 -160
WIRE 208 -128 208 -160
WIRE 128 -16 128 -48
WIRE 208 -16 208 -48
WIRE 128 80 128 48
WIRE 128 80 96 80
WIRE 208 80 208 48
WIRE 208 80 128 80
WIRE 288 80 208 80
WIRE 544 80 288 80
WIRE 96 112 96 80
WIRE 208 112 208 80
WIRE 48 128 0 128
WIRE 288 128 288 80
WIRE 48 176 0 176
WIRE 96 224 96 192
WIRE 144 224 96 224
WIRE 208 224 208 192
WIRE 208 224 144 224
WIRE 288 224 288 192
WIRE 288 224 208 224
WIRE 144 240 144 224
FLAG 144 240 0
FLAG 0 128 InP
IOPIN 0 128 In
FLAG 0 176 InM
IOPIN 0 176 In
FLAG 544 80 Out
IOPIN 544 80 Out
FLAG 128 -160 VDD
FLAG 208 -160 VSS
SYMBOL g 96 96 R0
SYMATTR InstName G1
SYMATTR Value {VDol/R}
SYMBOL res 192 96 R0
SYMATTR InstName R1
SYMATTR Value {R}
SYMBOL cap 272 128 R0
SYMATTR InstName C1
SYMATTR Value {VDol/GBW/Pi2}
SYMBOL diode 192 -16 R0
SYMATTR InstName D1
SYMATTR Value LIMITV
SYMBOL diode 144 48 R180
WINDOW 0 24 64 Left 2
WINDOW 3 26 3 Left 2
SYMATTR InstName D2
SYMATTR Value LIMITV
SYMBOL voltage 128 -144 R0
SYMATTR InstName V3
SYMATTR Value 2
SYMBOL voltage 208 -144 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V4
SYMATTR Value -2
TEXT -224 -56 Left 2 !;dc V1 -0.1 0.1 0.001
TEXT -224 -24 Left 2 !VSS VSS 0 DC -5\nVDD VDD 0 DC 5
TEXT -232 32 Left 2 !V1 INP 0 DC 0 AC 1\nV2 INM 0 DC 0
TEXT -232 224 Left 2 !.param VDol=100k
TEXT -232 264 Left 2 !.param GBW 1E6
TEXT -240 304 Left 2 !.model LIMITV D(Is=2.52n Rs=.00000001 N=1.752 )
TEXT -232 -88 Left 2 !.ac oct 10 1 1E9
TEXT -232 192 Left 2 !.param R 1
TEXT -232 88 Left 2 !.param Pi2 6.2831530717959

Es gibt die Differenzleerlaufverstärkung (open loop) VDol.

Realer Operationsverstärker

Kenngröße	Bipolar 741	CMOS TLC272	Typisch	Ideal
Differenzverstärkung $A_{D}$	$10^{5}$	$2.7 \cdot 10^{4}$	$10^{4}…10^{6}$	$\infty$
Gleichtaktunterdrückung G	$3 \cdot 10^{4}$	1000	$10^{3}…10^{6}$	$\infty$
Differenzeingangswiderstand $r_{D}$	$1M\Omega$	$> 1G\Omega$	$10^{5}…10^{7} \Omega$	$\infty$
Gleichtaktwiderstand	$1G \Omega$	$> 1G\Omega$	$> 100 R_D$	$\infty$
Ausgangswiderstand	$1k\Omega$	$500\Omega$	$70k \Omega ..1k \Omega$	0
Offsetspannung $V_{OS}$	1mV	1mV	0.5..5mV	0
Offsetstrom $I_{OS}$	$< I_{E}$	7pA	$< I_{E}$	0
Eingangsruhestrom $I_{E}$	80nA	40pA	20..200nA	0
Gleichtaktaussteuerbereich	$0.8\cdot U_B$	$0.8\cdot U_B$	$0.8\cdot U_B$	$U_{B}$
Ausgangssteuerbereich	$0.8\cdot U_B$	$0.8\cdot U_B$	$0.8\cdot U_B$	$U_{B}$
Slew rate SR		$4V / \mu s$	$0.5..50V/ \mu s$	$\infty$
Transitfrequenz Verstärkungsbandbreiteprodukt	1 MHz	2MHz	1..10 MHz	$\infty$
Betriebsstromaufnahme	1.7 mA	0.8mA	1 mA	0

Slew Rate

Die maximale Änderungsgeschwindigkeit der Ausgangsspannung
Einheit: $V/ \mu s$
$U_{0}$ :Amplitude einer Sinusschwingung
Die Slew Rate kann die maximale Frequenz, bei der der Operationsverstärker das Eingangssignal noch verstärkt, begrenzen.

$S_{R} = \frac{d U_{a}}{dt}$

$S_{R} = \frac{d U_{0} sin \left( \omega t \right)}{dt} = \omega \cdot U_{0} cos \left( \omega t \right)$

$\omega_{max} < \frac{S_{R}}{U_{0}}$

$f_{max} = \frac{\omega}{2 \cdot \pi} < \frac{S_{R}}{2 \cdot \pi \cdot U_{0}}$

$f_{max}(TLC272, 5V) = \frac{4 V\mu s^{-1}}{2 \cdot \pi \cdot 5 V}$

$f_{max}(TLC272, 5V) = 127 kHz$

Fragen

Wie sieht das Schaltsymbol eines Operationsverstärkers aus?
Welche Eigenschaften hat der ideale und reale Operationsverstärker?
Was ist eine Slew Rate?
Wie modelliert man einen Offset?

Übung Frequenzgang

Berechnen Sie die komplexe Übertragungsfunktion $\underline{U}_{A} / \underline{U}_{E}$ für folgenden Schaltkreis.
Stellen Sie Betrag in dB und Phase in Excel dar.
Wie groß ist Betrag in dB und Phase für f = 0 und $f \rightarrow \infty$ ?
Bei welcher Frequenz ist der Phasenwinkel 45°?
Bei welcher Frequenz ist der Betrag der Übertragungsfunktion -3dB?
Welche Steigung hat der Betrag in dB der Übertragungsfunktion für große Frequenzen?
Verifizieren Sie Ihre Ergebnisse mit LTSPICE.

$A_{f} = 20 log| \frac{\underline{U}_A}{\underline{U}_E} | dB$

Frequenz.asc

Version 4
SHEET 1 880 680
WIRE 112 80 16 80
WIRE 256 80 192 80
WIRE 16 128 16 80
WIRE 256 128 256 80
WIRE 16 224 16 208
WIRE 128 224 16 224
WIRE 256 224 256 192
WIRE 256 224 128 224
WIRE 128 240 128 224
FLAG 128 240 0
FLAG 256 80 UA
FLAG 16 80 UE
SYMBOL voltage 16 112 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value 1
SYMATTR Value2 AC 1
SYMBOL res 208 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL cap 240 128 R0
SYMATTR InstName C1
SYMATTR Value 22n
TEXT 8 280 Left 2 !.ac dec 10 1 10Meg

Übung Frequenzgang

$A_{f} = 20 log| \frac{\underline{U}_A}{\underline{U}_E} | dB$

$\frac{\underline{U}_A}{\underline{U}_E} = \frac{\frac{1}{j \omega C_1}}{R_1 + \frac{1}{j \omega C_1}} = \frac{1}{1 + j \omega C_1 \cdot R_1}$

$A_{f} = 20 log| \frac{\underline{U}_A}{\underline{U}_E} | dB = 20 log \frac{1}{\sqrt{1 + \left( \omega C_1 \cdot R_1 \right)^2}} dB$

$\omega = 0; A_{f} = 20 log \frac{1}{\sqrt{1 + \left( 0 \cdot C_1 \cdot R_1 \right)^2}} dB = 0 dB$

$\omega = \frac{1}{C_1 \cdot R_1} ; A_{f} = 20 log \frac{1}{\sqrt{1 + \left( \frac{1}{C_1 \cdot R_1} \cdot C_1 \cdot R_1 \right)^2}} dB = 20 log \frac{1}{\sqrt{2}} = -3 dB$

$\omega >> \frac{1}{C_1 \cdot R_1} ; A_{f} = 20 log \frac{1}{\omega} dB$
Ein Faktor 10 in der Frequenz bedeutet eine Differenz des Maßes von 20 dB.

Nächstes Mal:

20 Operationsverstärker

2020 09 07 Elektronik 3 19 Operationsverstärker Prof. Dr. Joerg Vollrath

Elektronik 3

19 Operationsverstärker

Prof. Dr. Jörg Vollrath

Video 19 Operationsverstärker 7.12.2020

Rückblick und Heute

Operationsverstärker

CMOS Operationsverstärker TLC272

CMOS Operationsverstärker TLC272 gebondeter Chip

Operationsverstärker: Schaltsymbol

Operationsverstärker: Eigenschaften und Übertragungskennlinie

Gleichtakteingangsspannung

Ersatzschaltbild

LTSPICE Modell

Realer Operationsverstärker

Slew Rate

Fragen

Übung Frequenzgang

Übung Frequenzgang

Nächstes Mal: