Elektronik 321 Anwendung OperationsverstärkerProf. Dr. Jörg Vollrath20 Operationsverstaerker |
Video der 21. Vorlesung 14.12.2020
|
Länge: 00:35:00 |
0:3:14 MOSFET Sättigungsgleichung in der Knotengleichung 0:5:48 MOSFET Gate und Drain verbunden 0:8:50 gm >> gd 0:9:5 Stromquelle -> gm 0:13:35 Übung 3 Aufgabe 3 0:15:35 Fliesst ein Strom in das Gate? 0:17:54 IDS3 = IDS1, VX = 2 VG 0:22:35 Aufgabe 4 0:24:19 VA Berechnung 0:27:22 WS2011 Aufgabe 3 0:28:7 Knotengleichung VB = 2 VA 0:30:8 Gleichung VB |
Video der 22. Vorlesung 16.12.2020
|
Länge: 01:04:00 |
0:0:0 Hochpass, Differenzierer, Übertragungsfunktion 0:3:1 Operationsverstärker mit Ersatzschaltbild 0:4:5 Knotengleichung 0:5:18 Ua/Ue = -jwRC 0:7:51 Hochpass 0:8:54 Differenzierer C=Q/U=I*t/U=Idt/dU 0:12:57 Hochpass mit Widerstand 0:16:16 Ergebnis, Rechnung, Betrag, Phase 0:19:36 Bodediagramm: Betrag, Phase 0:21:20 Integrator 0:24:57 w gegen 0 0:29:9 Hochpass und Tiefpass ergeben einen Bandpass 0:31:19 Aufgabe 5 Klausur WS2011 0:32:44 Schaltbild 0:36:0 Gleichspannungsverstärkung 0:39:11 Übertragungsfunktion 0:42:46 Eckfrequenzen 0:47:9 LTSPICE Verifikation des Ergebnisses 0:48:36 3 dB Eckfrequenz 0:50:31 Der Phasenverlauf 0:52:21 Simulation Zeitverlauf 0:56:38 opamp.sub |
Rückblick und Heute
Operationsverstärker
- Frequenzgang, Gegenkopplung
- Addierer, Subtrahierer
- Heute:
- Differenzierer (Hochpass)
- Integrierer (Tiefpass)
- Stabilität Rückgekoppelter Systeme
Jaeger: Chap. 10 S.529 -
Der Operationsverstärker ist eine integrierte Schaltung mit einem Differenzverstärker
am Eingang und eine gesteuerten Spannungsquelle als Ausgangsstufe.
Es fliesst kein Strom in die Eingänge des Operationsverstärkers.
Der Eingangswiderstand ist deshalb unendlich.
Wird der Operationsverstärker mit einer negativen Rückkopplung betrieben, wird die Verstärkung in erster Näherung nur von den externen Elementen bestimmt.
Die Differenzspannung zwischen positiven und negativen Eingang wird fast Null.
Mit den Annahmen dass kein Strom in den Operationsverstärker fliesst und die Differenzspannung Null ist, kann man Knoten und Maschengleichungen zur Bestimmung der Verstärkung aufstellen.
Nachdem einfache Beschaltungen mit ohmschen Widerständen betrachtet wurden, werden jetzt Beschaltungen mit Kapazitäten untersucht.
Induktivitäten werden hier nicht betrachtet, da Sie in der Praxis mit genau definierten Werten und integriert auf einem Chip schwer zu realisieren sind.
Diese Schaltungen werden mit komplexer Rechnung analysiert und eine Übertragungsfunktion mit Polen und Nullstellen aufgestellt.
Die Pole und Nullstellen der Übertragungsfunktion erlauben es, den Frequenzgang mit den Grenzfrequenzen einfach zu bestimmen und Aussagen über die Stabilität des Systems zu geben.
Übertragungsfunktionen finden auch in der Regelungstechnik Anwendung.
Die Übertragungsfunktion wird so umgeformt, dass man Polynome von jω im Zähler und Nenner stehen hat.
Dann werden die Polynome zu Null gesetzt, um Nullstellen für den Zähler und Polstellen für den Nenner zu erhalten.
An den Nullstellen verändert sich die Phase der Übertragungsfunktion um 90° und ist genau 45°, da Realteil und Imaginärteil genau gleich gross sind.
Die Steigung der Übertragungsfunktion verändert sich um +20 dB/Dekade.
An den Polstellen verändert sich die Phase der Übertragungsfunktion um -90° und ist genau -45°.
Die Steigung der Übertragungsfunktion verändert sich um -20 dB/Dekade.
Es fliesst kein Strom in die Eingänge des Operationsverstärkers.
Der Eingangswiderstand ist deshalb unendlich.
Wird der Operationsverstärker mit einer negativen Rückkopplung betrieben, wird die Verstärkung in erster Näherung nur von den externen Elementen bestimmt.
Die Differenzspannung zwischen positiven und negativen Eingang wird fast Null.
Mit den Annahmen dass kein Strom in den Operationsverstärker fliesst und die Differenzspannung Null ist, kann man Knoten und Maschengleichungen zur Bestimmung der Verstärkung aufstellen.
Nachdem einfache Beschaltungen mit ohmschen Widerständen betrachtet wurden, werden jetzt Beschaltungen mit Kapazitäten untersucht.
Induktivitäten werden hier nicht betrachtet, da Sie in der Praxis mit genau definierten Werten und integriert auf einem Chip schwer zu realisieren sind.
Diese Schaltungen werden mit komplexer Rechnung analysiert und eine Übertragungsfunktion mit Polen und Nullstellen aufgestellt.
Die Pole und Nullstellen der Übertragungsfunktion erlauben es, den Frequenzgang mit den Grenzfrequenzen einfach zu bestimmen und Aussagen über die Stabilität des Systems zu geben.
Übertragungsfunktionen finden auch in der Regelungstechnik Anwendung.
Die Übertragungsfunktion wird so umgeformt, dass man Polynome von jω im Zähler und Nenner stehen hat.
Dann werden die Polynome zu Null gesetzt, um Nullstellen für den Zähler und Polstellen für den Nenner zu erhalten.
An den Nullstellen verändert sich die Phase der Übertragungsfunktion um 90° und ist genau 45°, da Realteil und Imaginärteil genau gleich gross sind.
Die Steigung der Übertragungsfunktion verändert sich um +20 dB/Dekade.
An den Polstellen verändert sich die Phase der Übertragungsfunktion um -90° und ist genau -45°.
Die Steigung der Übertragungsfunktion verändert sich um -20 dB/Dekade.
Hochpass, Differenzierer
|
I_C = I_R
Differentialgleichung: C \frac{d U_e}{dt} = - \frac{U_a}{R} U_a = - R \cdot C \frac{d U_e}{dt} \tau = R \cdot C Komplexe Rechnung: \underline{I}_C = \underline{I}_R j \omega C \underline{U}_e = - \frac{\underline{U}_a}{R} \frac{\underline{U}_a}{\underline{U}_e} = - j \omega C \cdot R A_v = 20 log | - \omega C \cdot R |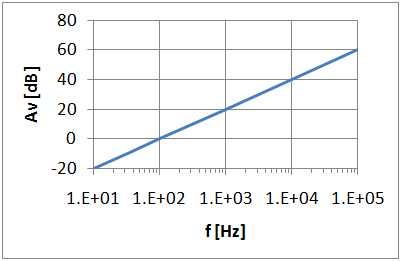 
|
Version 4 SHEET 1 880 680 WIRE 112 16 96 16 WIRE 0 48 -32 48 WIRE 96 48 96 16 WIRE 96 48 64 48 WIRE 96 80 96 48 WIRE 112 80 96 80 WIRE 192 96 192 16 WIRE 192 96 176 96 WIRE 208 96 192 96 WIRE 112 112 96 112 WIRE 96 144 96 112 FLAG -32 48 Ve IOPIN -32 48 In FLAG 208 96 Va IOPIN 208 96 Out FLAG 96 144 0 SYMBOL Opamps\\opamp 144 32 R0 SYMATTR InstName U1 SYMBOL res 208 0 R90 WINDOW 0 0 56 VBottom 0 WINDOW 3 32 56 VTop 0 SYMATTR InstName R SYMATTR Value "" SYMBOL cap 64 32 R90 WINDOW 0 0 32 VBottom 0 WINDOW 3 32 32 VTop 0 SYMATTR InstName C SYMATTR Value "" Version 4 SymbolType CELL LINE Normal -32 32 32 64 LINE Normal -32 96 32 64 LINE Normal -32 32 -32 96 LINE Normal -28 48 -20 48 LINE Normal -28 80 -20 80 LINE Normal -24 84 -24 76 WINDOW 0 0 32 Left 0 SYMATTR Prefix X SYMATTR Description Ideal single-pole operational amplifier. You must .lib opamp.sub SYMATTR Value opamp SYMATTR SpiceLine Aol=100K SYMATTR SpiceLine2 GBW=10Meg PIN -32 48 NONE 0 PINATTR PinName invin PINATTR SpiceOrder 1 PIN -32 80 NONE 0 PINATTR PinName noninvin PINATTR SpiceOrder 2 PIN 32 64 NONE 0 PINATTR PinName out PINATTR SpiceOrder 3 |
Es wird die Knotengleichung aufgestellt.
Für die Ströme wird zum Einen die Differentialgleichung und zum Anderen das ohmsche Gesetz im Komplexen angewendet.
Es ergibt sich bei der Differentialgleichung das zeitliche Verhalten der Ausgangsspannung.
Im Komplexen wird das Verhältnis der Ausgangsspannung zur Eingangsspannung für die Übertragungsfunktion gebildet.
Die Lösung der Differentialgleichung zeigt das Verhalten als Differenzierer.
Nur die Änderung der Eingangsspannung ergibt eine von Null verschiedene Ausgangsspannung.
Keine Gleichspannung wird übertragen. Dies ist das gleiche Verhalten, dass schon bei den Verstärkergrundschaltungen angewendet wurde.
Die Übertragungsfunktion zeigt das Verhalten eines Hochpasses. Je höher die Frequenz desto größer ist die Verstärkung.
In der Realität wird die Verstärkung von der Übertragungsfunktion des Operationsverstärkers und der Versorgungsspannung begrenzt.
Die Ausgangsspannung ist um -90° (-jω) in der Phase verschoben.
Für die Ströme wird zum Einen die Differentialgleichung und zum Anderen das ohmsche Gesetz im Komplexen angewendet.
Es ergibt sich bei der Differentialgleichung das zeitliche Verhalten der Ausgangsspannung.
Im Komplexen wird das Verhältnis der Ausgangsspannung zur Eingangsspannung für die Übertragungsfunktion gebildet.
Die Lösung der Differentialgleichung zeigt das Verhalten als Differenzierer.
Nur die Änderung der Eingangsspannung ergibt eine von Null verschiedene Ausgangsspannung.
Keine Gleichspannung wird übertragen. Dies ist das gleiche Verhalten, dass schon bei den Verstärkergrundschaltungen angewendet wurde.
Die Übertragungsfunktion zeigt das Verhalten eines Hochpasses. Je höher die Frequenz desto größer ist die Verstärkung.
In der Realität wird die Verstärkung von der Übertragungsfunktion des Operationsverstärkers und der Versorgungsspannung begrenzt.
Die Ausgangsspannung ist um -90° (-jω) in der Phase verschoben.
Hochpass, Differenzierer
|
\frac{\underline{U}_e}{R_1 + \frac{1}{j \omega C}}
= - \frac{\underline{U}_a}{R}
\frac{\underline{U}_a}{\underline{U}_e} = - \frac{R}{R_1 + \frac{1}{j \omega C}} \frac{\underline{U}_a}{\underline{U}_e} = - \frac{R}{R_1} \frac{j \omega}{ j \omega + \frac{1}{C R_1}}
Betrag:
\left| \frac{\underline{U}_a}{\underline{U}_e} \right| = \frac{R}{R_1} \frac{\omega}{ \sqrt{ \omega^2 + \left( \frac{1}{C R_1} \right)^2 }} 20 log \left| \frac{\underline{U}_a}{\underline{U}_e} \right| = 20 log \frac{R}{R_1} + 20 log \omega - 20 log \sqrt{ \omega^2 + \left( \frac{1}{C R_1} \right)^2 } Phase: - j \omega gibt einen Winkel von -90°. \phi = -90° - arctan(\frac{\omega}{\frac{1}{C \cdot R_1}}) \phi = - 90° - arctan( \omega \cdot C \cdot R_1 ) |
Version 4 SHEET 1 880 680 WIRE 112 16 96 16 WIRE -64 48 -80 48 WIRE 96 48 96 16 WIRE 96 48 80 48 WIRE 96 80 96 48 WIRE 112 80 96 80 WIRE 192 96 192 16 WIRE 192 96 176 96 WIRE 208 96 192 96 WIRE 112 112 96 112 WIRE 96 144 96 112 FLAG -80 48 Ve IOPIN -80 48 In FLAG 208 96 Va IOPIN 208 96 Out FLAG 96 144 0 SYMBOL Opamps\\opamp 144 32 R0 SYMATTR InstName U1 SYMBOL res 208 0 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R SYMATTR Value "" SYMBOL cap 80 32 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C SYMATTR Value "" SYMBOL res 32 32 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R1 |
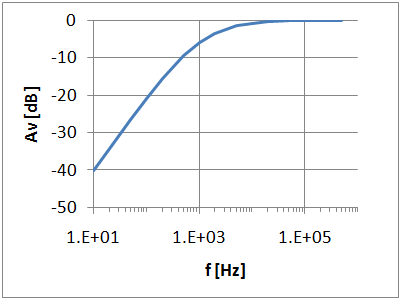
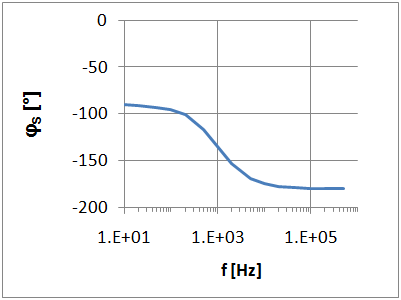
Integrator
|
Schalter für die Initialisierung, Anfangsbedingung
U_a = - \frac{1}{RC} \int_{t_0}^{t1} U_e (t) dt + U_a(t_0)
\frac{\underline{U}_e }{R_1} = - \underline{U}_a j \omega C \frac{\underline{U}_a }{\underline{U}_e} = - \frac{1}{j \omega C R_1} |
Version 4 SHEET 1 880 680 WIRE 128 -96 96 -96 WIRE 192 -96 176 -96 WIRE 96 16 96 -96 WIRE 112 16 96 16 WIRE 192 16 192 -96 WIRE 192 16 176 16 WIRE -48 48 -80 48 WIRE 96 48 96 16 WIRE 96 48 32 48 WIRE 96 80 96 48 WIRE 112 80 96 80 WIRE 192 96 192 16 WIRE 192 96 176 96 WIRE 208 96 192 96 WIRE 112 112 96 112 WIRE 96 144 96 112 FLAG -80 48 Ve IOPIN -80 48 In FLAG 208 96 Va IOPIN 208 96 Out FLAG 96 144 0 SYMBOL Opamps\\opamp 144 32 R0 SYMATTR InstName U1 SYMBOL cap 176 0 R90 WINDOW 0 0 32 VBottom 0 WINDOW 3 32 32 VTop 0 SYMATTR InstName C SYMATTR Value "" SYMBOL res 48 32 R90 WINDOW 0 0 56 VBottom 0 WINDOW 3 32 56 VTop 0 SYMATTR InstName R1 SYMATTR Value "" LINE Normal 176 -112 128 -96 LINE Normal 176 -112 176 -112 |
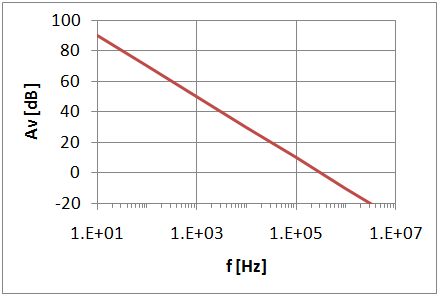
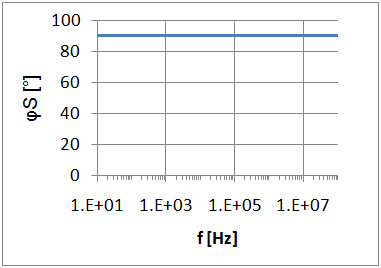
Integrator
|
\frac{\underline{U}_e}{R_1} = - \underline{U}_a \left( j \omega C + \frac{1}{R} \right)
\frac{\underline{U}_a}{\underline{U}_e} = - \frac{1}{ j \omega C R_1 + \frac {R_1}{R}}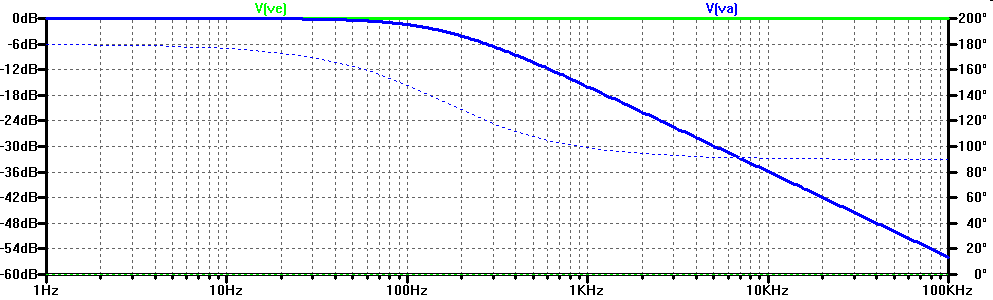 
|
Version 4 SHEET 1 880 680 WIRE 128 -112 96 -112 WIRE 192 -112 176 -112 WIRE 96 -64 96 -112 WIRE 112 -64 96 -64 WIRE 192 -64 192 -112 WIRE 96 16 96 -64 WIRE 112 16 96 16 WIRE 176 16 160 16 WIRE 192 16 192 -64 WIRE 192 16 176 16 WIRE -48 48 -80 48 WIRE 96 48 96 16 WIRE 96 48 32 48 WIRE 96 80 96 48 WIRE 112 80 96 80 WIRE 192 96 192 16 WIRE 192 96 176 96 WIRE 208 96 192 96 WIRE 112 112 96 112 WIRE 96 144 96 112 FLAG -80 48 Ve IOPIN -80 48 In FLAG 208 96 Va IOPIN 208 96 Out FLAG 96 144 0 SYMBOL Opamps\\opamp 144 32 R0 SYMATTR InstName U1 SYMBOL res 208 -80 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 50 61 VBottom 2 SYMATTR InstName R SYMATTR Value 1k SYMBOL cap 176 0 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 54 33 VBottom 2 SYMATTR InstName C SYMATTR Value 1� SYMBOL res 48 32 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 64 57 VBottom 2 SYMATTR InstName R1 SYMATTR Value 1k TEXT -152 -120 Left 2 !.include opamp.sub TEXT -152 -88 Left 2 !VE VE 0 DC 1 AC 1 TEXT -152 -56 Left 2 !.ac dec 10 1 100k LINE Normal 176 -128 128 -112 LINE Normal 176 -112 176 -112 |
Aufgabe Klausur WS2011
|
Gegeben sei folgende Operationsverstärkerschaltung.
Bestimmen Sie die Gleichspannungsverstärkung. (2 Punkte) Bestimmen Sie den Eingangswiderstand. (1 Punkt) Bestimmen Sie die Übertragungsfunktion. (2 Punkte) Bestimmen Sie die 3dB Eckfrequenz(en). (2 Punkte)
\frac{U_{out}}{U_{in}} = \frac{R_1 + R_2}{R_1} = \frac{112k + 8k}{8k} = 15 A_V = 20 log 15 dB = 23.5 dB R_e = \infty \frac{\underline{U}_{out}}{\underline{U}_{in}} = \frac{R_1 + \frac{R_2}{1 + j \omega C R_2}}{R_1} = 1 + \frac{R_2}{R_1} \frac{1}{1 + j \omega C R_2} = \frac{R_2}{R_1} \frac{\frac{R_1}{R_2} \left( 1 + j \omega C R_2 \right) + 1 }{1 + j \omega C R_2} = \frac{R_2}{R_1} \frac{ 1 + \frac{R_1}{R_2} + j \omega C R_1 }{1 + j \omega C R_2} f_1 = \frac{\omega_1}{2 \pi} = \frac{1}{2 \pi C R_2} = 1.42 kHz f_2 = \frac{ 1 + \frac{R_1}{R_2} }{2 \pi C R_1} = 21 kHz |
Version 4 SHEET 1 880 680 WIRE 160 112 112 112 WIRE 272 128 224 128 WIRE 368 128 272 128 WIRE 416 128 368 128 WIRE 160 144 128 144 WIRE 368 144 368 128 WIRE 128 208 128 144 WIRE 272 208 128 208 WIRE 368 208 272 208 WIRE 272 240 272 208 WIRE 272 336 272 320 FLAG 272 336 0 FLAG 112 112 Vin FLAG 416 128 Vout SYMBOL Opamps\\opamp 192 192 M180 SYMATTR InstName U1 SYMBOL res 256 224 R0 SYMATTR InstName R1 SYMATTR Value 8k SYMBOL res 256 112 R0 SYMATTR InstName R2 SYMATTR Value 112k SYMBOL cap 352 144 R0 WINDOW 0 29 11 Left 2 SYMATTR InstName C1 SYMATTR Value 1n TEXT 72 80 Left 2 !.include opamp.sub TEXT 64 48 Left 2 !.ac dec 10 1 100k TEXT 56 8 Left 2 !VIN VIN 0 SIN(0 1 1.42k) AC 1 TEXT 312 48 Left 2 !;tran 10m |
Es liegt eine negative Rückkopplung vor. Ein Teil des Ausgangssignals
wird am negativen Eingang des Operationsverstärkers angelegt.
Die Differenzspannung am Eingang ist näherungsweise Null.
Am Widerstand R1 liegt die Spannung Uin.
Nun wird die Spannungsteilerformel angewendet.
Für eine reine Gleichspannungsbetrachtung wird die Kapazität weggelassen und durch eine Unterbrechung ersetzt.
Die AC Simulation mit LTSPICE bestätigt das Ergebnis der Rechnung.
Die Differenzspannung am Eingang ist näherungsweise Null.
Am Widerstand R1 liegt die Spannung Uin.
Nun wird die Spannungsteilerformel angewendet.
Für eine reine Gleichspannungsbetrachtung wird die Kapazität weggelassen und durch eine Unterbrechung ersetzt.
Die AC Simulation mit LTSPICE bestätigt das Ergebnis der Rechnung.