Elektronik02 GroessenProf. Dr. Jörg Vollrath |

|
Übersicht, Lernziele
- Ladung, Spannung, Strom, Leistung
- Spannungsquelle, Widerstand
- Gleichung: Ohmsches Gesetz
- Schaltzeichen
- Messung
Die Grundgrößen der Elektrotechnik sind Spannung U in Volt (V),
Strom I in Amper (A) und die Ladung Q in Coulomb (C).
Bewegliche elektrische Ladung bewegt sich in einem leitendem Material (Metall, Halbleiter).
Die Spannung bestimmt die Bewegungsrichtung und die bewegte Ladung bestimmt den Strom.
Die Leistung P in Watt (W) ergibt sihc als abgeleitete Größe aus U · I.
Eine Spannung wird durch eine Spannungsquelle mit 2 Anschlüssen erzeugt.
Die 2 Anschlüsse werden an einen Verbraucher angeschlossen.
Der einfachste Verbraucher ist ein ohmscher Widerstand R.
Der Zusammenhang zwischen Spannung Strom und Widerstand wird durch das ohmsche Gestz beschrieben.
Für die einzelnen Elemente der Elektrotechnik gibt es Schaltzeichen mit denen ein Schaltplan gezeichnet wird.
In einer Schaltung werden Spannungen und Ströme berechnet und gemessen. Der elektrischen Messung zur Verifikation der Funktion kommt eine besondere Bedeutung zu.
Mit Spannung und Strom wird Energie und Information übertragen.
Bewegliche elektrische Ladung bewegt sich in einem leitendem Material (Metall, Halbleiter).
Die Spannung bestimmt die Bewegungsrichtung und die bewegte Ladung bestimmt den Strom.
Die Leistung P in Watt (W) ergibt sihc als abgeleitete Größe aus U · I.
Eine Spannung wird durch eine Spannungsquelle mit 2 Anschlüssen erzeugt.
Die 2 Anschlüsse werden an einen Verbraucher angeschlossen.
Der einfachste Verbraucher ist ein ohmscher Widerstand R.
Der Zusammenhang zwischen Spannung Strom und Widerstand wird durch das ohmsche Gestz beschrieben.
Für die einzelnen Elemente der Elektrotechnik gibt es Schaltzeichen mit denen ein Schaltplan gezeichnet wird.
In einer Schaltung werden Spannungen und Ströme berechnet und gemessen. Der elektrischen Messung zur Verifikation der Funktion kommt eine besondere Bedeutung zu.
Mit Spannung und Strom wird Energie und Information übertragen.
Größen
- Ladung: Q in C (Coulomb)
- Spannung: U in V (Volt), Strom I in A (Ampere)
- Leistung P in W (Watt)
- Widerstand: R (X) in Ω (Ohm)
- Induktivität: L in H (Henry)
- Kapazität: C in F (Farad)
- Vorsatzzeichen
kleiner: m (milli), µ (micro), n (nano), p (pico), f (femto), a (ato)
größer: k (kilo), M (Mega), G (Giga), T (Tera), P (Penta)
Jede elektrische Größe hat einen Bezeichner, eine Einheit und ein Vorsatzzeichen.
Mit den Vorsatzzeichen ist es leichter eine Größe einzuordnen.
Mit den Vorsatzzeichen ist es leichter eine Größe einzuordnen.
Vorsatzzeichen
Vorsatzzeichen verhalten sich wie Zahlenwerte einer Variablen.
m = 10-3; µ = 10-6; n = 10-9; p = 10-12; f = 10-15; a = 10-18
k = 103; M = 106; G = 109; T = 1012;
Beispiel:
0.4507 mA = 0.4507 · 10-3 A = 450.7 · 10-6 A = 450.7 µA
Die Vorsatzzeichen lernt man auswendig.
Elektronik
| Kondensator | Stromfluß | |||
| Größe | Ladung | elektrische Feld | Spannung | Strom |
| Zeichen | Q | E | U | I |
| Einheit | C | V | A | |
| Coulomb | Volt | Amper | ||
 |
 | |||
Kapazität\( I = C \frac{dU}{dt} \) \( C = \frac{Q}{U} = \frac{I \cdot dt}{dU} \) |
Induktivität\( U = L \frac{dI}{ dt} \) | |||
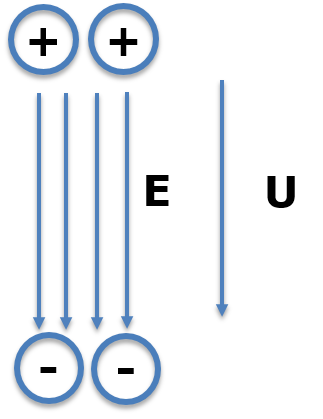
Das Bild soll etwas den Hintergrund der Elektrotechnik erläutern.
Es gibt positive und negative Ladungen dargestellt als Kreis mit Plus oder Minus Zeichen.
Es gibt die Elementarladung mit 1.6 · 10-19 C.
Gleiche Ladungen stoßen sich ab, unterschiedliche Ladungen ziehen sich an.
Es entsteht ein elektrisches Feld E (Pfeile) und Kräfte wirken auf die Ladungen.
Entlang des Feldes entsteht eine Spannung U (Pfeil):
\( U = \int{E} ds \)
Man kann einen Kondensator zur Ladungsspeicherung bauen.
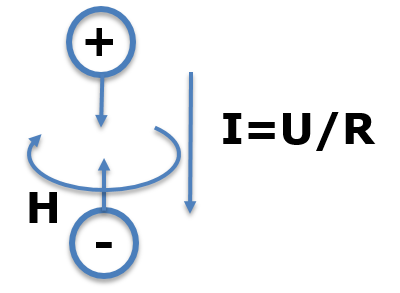
Bewegte Ladungen stellen einen Strom dar.
\( I = \frac{dQ}{dt} \)
Eine gewisse Ladungsmenge dQ bewegt sich in einer Zeit dt.
Ladungen können sich in einem Leiter bewegen.
Der Leiter hat einen Widerstand R, der von Material, Länge und Querschnitt abhängt.
U = I · R
Bewegte Ladung erzeugt ein Magnetfeld H. Auf eine bewegte Ladung im Magnetfeld wirkt eine Kraft.
Man kan eine Induktivität, einen Transformator, einen Generator oder einen Motor bauen.
Es gibt positive und negative Ladungen dargestellt als Kreis mit Plus oder Minus Zeichen.
Es gibt die Elementarladung mit 1.6 · 10-19 C.
Gleiche Ladungen stoßen sich ab, unterschiedliche Ladungen ziehen sich an.
Es entsteht ein elektrisches Feld E (Pfeile) und Kräfte wirken auf die Ladungen.
Entlang des Feldes entsteht eine Spannung U (Pfeil):
\( U = \int{E} ds \)
Man kann einen Kondensator zur Ladungsspeicherung bauen.
Bewegte Ladungen stellen einen Strom dar.
\( I = \frac{dQ}{dt} \)
Eine gewisse Ladungsmenge dQ bewegt sich in einer Zeit dt.
Ladungen können sich in einem Leiter bewegen.
Der Leiter hat einen Widerstand R, der von Material, Länge und Querschnitt abhängt.
U = I · R
Bewegte Ladung erzeugt ein Magnetfeld H. Auf eine bewegte Ladung im Magnetfeld wirkt eine Kraft.
Man kan eine Induktivität, einen Transformator, einen Generator oder einen Motor bauen.
Bekannte Quellen
Welche Spannungsquellen kennen Sie?
Generator, Batterie
Steckdose, Stecker, USB Stecker, Rundstecker
Schaltzeichen Quellen
Ideale und reale Spannungsquelle
|
Spannung U1 V1 englisch U(V1) Reale Spannungsquelle Serienwiderstand R1, Ri |
|
Strom I1 Reale Stromquelle Parallelwiderstand R1, Ri |
Reale physikalische Bauelemente abstrahiert man in der Elektrotechnik durch Schaltzeichen.
Hier sieht man eine ideal Spanungsquelle, eine ideale Stromquelle und einen Widerstand.
Leider gibt es unterschiedliche Schaltzeichen für ein und das selbe Bauelement.
Eine Spannungsquelle wird entweder durch einen Kreis mit einer senkrechten Linie und einem Pfeil dargestellt, oder durch einen Kreis mit Plus und Minus Symbol.
Die Zahl 3 gibt den Spannungswert an und ein Name V1 zur Identifizierung des Eelemnts wird verwendet.
Weiterhin kann man einen Widerstand R1 mit dem Wert 10 Ω und einen Widerstand mit 100 kΩ dargestellt mit einer gezackten Linie sehen.
Eine Stromquelle wird durch einen Kreis mit horizontaler Linie und einem Pfeil oder durch einen Kreis mit senkrechtem Pfeil dargestellt.
Auch hier sieht man einen Namen I1 und einen Wert 10m.
Eine reale Spannungsquelle hat einen Serienwiderstand, eine reale Stromquelle hat einen Parallelwiderstand.
Leider gibt es unterschiedliche Schaltzeichen für ein und das selbe Bauelement.
Eine Spannungsquelle wird entweder durch einen Kreis mit einer senkrechten Linie und einem Pfeil dargestellt, oder durch einen Kreis mit Plus und Minus Symbol.
Die Zahl 3 gibt den Spannungswert an und ein Name V1 zur Identifizierung des Eelemnts wird verwendet.
Weiterhin kann man einen Widerstand R1 mit dem Wert 10 Ω und einen Widerstand mit 100 kΩ dargestellt mit einer gezackten Linie sehen.
Eine Stromquelle wird durch einen Kreis mit horizontaler Linie und einem Pfeil oder durch einen Kreis mit senkrechtem Pfeil dargestellt.
Auch hier sieht man einen Namen I1 und einen Wert 10m.
Eine reale Spannungsquelle hat einen Serienwiderstand, eine reale Stromquelle hat einen Parallelwiderstand.
Widerstand und Ohmsches Gesetz
U : Spannung in V R : ohmscher Widerstand in Ω I : Strom in A 5 V = 10 kΩ · 500 µA \( G = \frac{1}{R} \) Leitwert in S |
Man sieht die gezackte Linie oder das Rechteck als Schaltsymbole
für einen Widerstand.
Eine Messung eines Widerstandes ergibt die gezeigte Darstellung der Spannung über dem Strom U(I).
Man sieht einen linearen Zusammenhang. Daraus ergibt sich das ohmsche Gesetz: U = I · R
Die Einheit Ω wird Omega ausgesprochen.
Der Leitwert wird in Siemens angegeben.
Im amerikanischen Sprachraum oder in Datenblättern findet man auch Ohm als Einheit des Widerstands und mho anstatt Siemens als Einheit des Leitwerts.
Eine Messung eines Widerstandes ergibt die gezeigte Darstellung der Spannung über dem Strom U(I).
Man sieht einen linearen Zusammenhang. Daraus ergibt sich das ohmsche Gesetz: U = I · R
Die Einheit Ω wird Omega ausgesprochen.
Der Leitwert wird in Siemens angegeben.
Im amerikanischen Sprachraum oder in Datenblättern findet man auch Ohm als Einheit des Widerstands und mho anstatt Siemens als Einheit des Leitwerts.
Schaltpläne
|
Bezugspunkt 0 V Masse GND | ||||
|
Knoten Name Der gleiche Name ersetzt eine Leitung | ||||
Eine reale Schaltung hat immer einen Bezugspunkt, eine Masse, GND an dem 0 V definiert sind.
Hier werden dafür drei unterschiedliche Symbole gezeigt. Alle haben die gleiche Funktion.
In Schaltungen werden öfters zur Übersichtlichkeit keine Leitungsverbindungen zwischen Bauelementen gezeichnet, sondern es werden Namen verwendet. Hier sind die beiden Punkte mit der Bezeichnung V1 verbunden.
Die Punkte zwischen zwei Bauelementen bezeichnet man als Knoten.
Hier werden dafür drei unterschiedliche Symbole gezeigt. Alle haben die gleiche Funktion.
In Schaltungen werden öfters zur Übersichtlichkeit keine Leitungsverbindungen zwischen Bauelementen gezeichnet, sondern es werden Namen verwendet. Hier sind die beiden Punkte mit der Bezeichnung V1 verbunden.
Die Punkte zwischen zwei Bauelementen bezeichnet man als Knoten.
Beispiel
|
Berechnen Sie für verschiedene Widerstände den Strom der gezeichneten Schaltung. V1 = 3 V, R1 = 10Ω, 100Ω, 1 kΩ, 10 kΩ, 100kΩ, 1 MΩ Zeichnen Sie die U(I) Kennlinie. |
| U / V | 3 | 3 | 3 | 3 | 3 | 3 |
| R / Ω | 10 | 100 | 1 k | 10 k | 100k | 1 M |
| I / A | 0.3 | 0.03 | 3 m | 0.3 m | 30 µ | 3 µ |
Die ideale Spannungsquelle kann beliebig viel Strom liefern, ohne das sich die Spannung ändert.
Spezifischer Widerstand und Leitfähigkeit
\( \left[\kappa\right]= \frac{1}{\Omega m} = \frac{S}{m} \frac{A}{V m} \) |
|
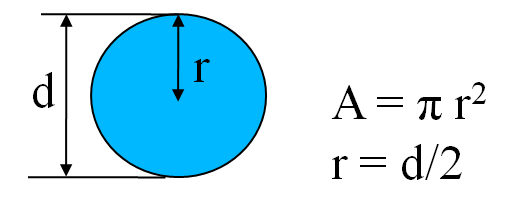
Ein Widerstand ergibt sich aus einem leitendem Material mit einem Querschnitt A und einer Länge l.
Jedes Material hat einen spezifischen Widerstand.
In de rElektrotechnik wird Kohlenstoff oder kupfer, Aluminium als Leiter und Widerstand eingesetzt.
Jedes Material hat einen spezifischen Widerstand.
In de rElektrotechnik wird Kohlenstoff oder kupfer, Aluminium als Leiter und Widerstand eingesetzt.
Praxisbezug Widerstand
|
|
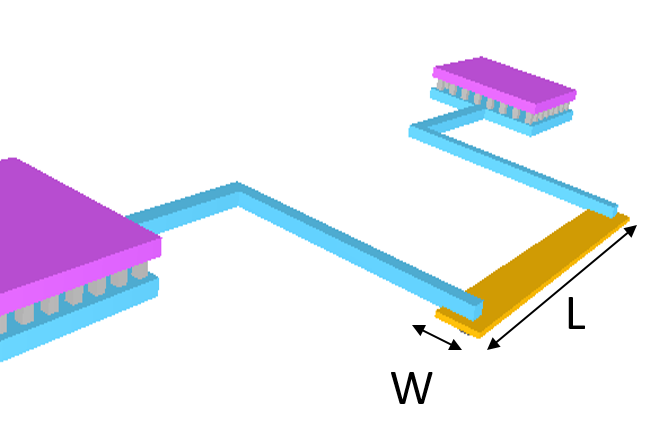
Das obere Bild zeigt eine Mikroskopaufnahme eines integrierten Widerstandes.
In der Mitte ist eine horizontale dotierte Widerstandsbahn zu sehen, die
rechts und links an Metallbahnen angeschlossen ist.
Im unteren Bild ist diese Struktur mit einer Weite W und einer Länge L
schematisch in einer 3D Ansicht zu sehen.
Tabelle spezifischer Widerstand bei 20 °C
| Material | Spezifischer Widerstand / Ω m |
Temperaturkoeffizient α20 / K-1 |
| Aluminium (Al) | 0.0278 · 10 -6 | 3.9 · 10 -3 |
| Eisen (Fe) | 0.1..0.15 · 10 -6 | 5.6 · 10 -3 |
| Kupfer (Cu) | 0.0176 · 10 -6 | 3.9 · 10 -3 |
| Konstantan | 0.5 · 10 -6 | 5 · 10 -5 |
| Silizium (Si) | 2.3 · 10 3 | -75 · 10 -3 |
| \( X(T) = X(T_{0}) \left(1 + \alpha (T - T_{0}) \right) \) |
T0 Bezugstemperatur
α Temperaturkoeffizient
Quelle:??
Eine temperaturabhängige Größe wird näherungsweise durch ein lineares Modell beschrieben.
Eine temperaturabhängige Größe wird näherungsweise durch ein lineares Modell beschrieben.
Zusammenfassung
- Sie kennen elektrische Größen und Vorsatzzeichen
- Sie kennen Widerstände, Spannungsquellen und Stromquellen.
Nächste Vorlesung:
03 Berechnungen