Elektronik 322 Analog-Digital-WandlerProf. Dr. Jörg Vollrath21 Digital-Analog-Wandler |
|
Video der 23. Vorlesung 12.1.2022
|
Länge: 1:02:43 |
0:0:45 Digital Analog Wandler R2R 0:3:10 LTSPICE Simulation 0:5:30 Widerstandsänderungen und Fehler 0:10:5 ADC Architekturen 0:12:6 AD Signalkette 0:19:55 Dual Slope Schaltungsanalyse 0:23:2 Simulation 0:26:53 Ein Schalter mit Transistoren 0:31:3 Zeitmessung mit Zähler 0:33:32 Rechnung Dual Slope, Schaltspannungen 0:38:37 Stromgleichung 0:42:17 Vergleich mit LTSPICE 0:44:6 Integrator 0:50:56 Gleichung des ADC 0:55:32 Schnelligkeit, Bandbreite 0:58:32 1 GHz Zähler, 1:1:25 Anzahl Bits und Frequenz 1:4:32 Flash ADC |
Übersicht
- ADC Architekturen
- Dual Slope ADC
- Flash ADC
ADC architectures, resolution and conversion rate
A graph with x axis frequency and y axis resolution shows applications.
Pipeline ADC: 8..16 Bits, 1MHz..4GHz
SAR ADC: 8..18 Bits, 20kHz..8MHz
Sigma Delta ADC: 12..24 Bits, 4Hz..40MHz
Source: QUINTÁNS et al.: METHODOLOGY TO TEACH ADVANCED A/D CONVERTERS, IEEE TRANS. ON EDUCATION, VOL. 53, NO. 3, AUGUST 2010
Investigation of distributer Digikey (01/2017):
Flash ADC (Results: 366): 10 Bit 50 MSps, Range 3..16Bit, 50kHz..26GHz
8 Bit 50kHz AD782 ADI, 3Bit 26GHz HMCAD5831LP9BE ADI, 8 Bit 1GHz MAX104CHC Maxim 16 Bit 166kHz AD7884AQ ADI
Pipeline ADC (Results: 3237): 12 Bit 125MSps, Range 6..16 Bit, 94k..2.6GHz
12 Bit 94kHz MAX1253BEUE+, 12 Bit 2.6GHz ADI, 6 Bit 90MHz MAX1011, 16 Bit 1GHz ADS54 TI
SAR ADC (Results: 8973): 12 Bit 1MSpS, Range 8.. 32Bit 1kSps..500 MSps
32 Bit 1MSps LTC2508 $16, 24 Bit 2MSps LTC2380 $54, 20 Bit 1.6 MSps MX11905 $30 8 Bit 500MSps ISLA118P5 Intersil $50, 8 Bit 3MSps MAX 11116 $2
Sigma Delta ADC(Results: 1928): 24 Bit 256kSps Range: 8..32 Bit , 3Sps..3.2GSps
16 Bit 3.2GSps(100MHz) AD6676 ADI $200, 16 Bit 160MSps(2.5MHz) AD9262 ADI $48, 12 Bit 3.3kSps ADS1015 TI $2, 32Bit 1MSps LTC2508 $17
Dual Slope (Results: 28): 15 Bit 30Sps
Pipeline ADC: 8..16 Bits, 1MHz..4GHz
SAR ADC: 8..18 Bits, 20kHz..8MHz
Sigma Delta ADC: 12..24 Bits, 4Hz..40MHz
Source: QUINTÁNS et al.: METHODOLOGY TO TEACH ADVANCED A/D CONVERTERS, IEEE TRANS. ON EDUCATION, VOL. 53, NO. 3, AUGUST 2010
Investigation of distributer Digikey (01/2017):
Flash ADC (Results: 366): 10 Bit 50 MSps, Range 3..16Bit, 50kHz..26GHz
8 Bit 50kHz AD782 ADI, 3Bit 26GHz HMCAD5831LP9BE ADI, 8 Bit 1GHz MAX104CHC Maxim 16 Bit 166kHz AD7884AQ ADI
Pipeline ADC (Results: 3237): 12 Bit 125MSps, Range 6..16 Bit, 94k..2.6GHz
12 Bit 94kHz MAX1253BEUE+, 12 Bit 2.6GHz ADI, 6 Bit 90MHz MAX1011, 16 Bit 1GHz ADS54 TI
SAR ADC (Results: 8973): 12 Bit 1MSpS, Range 8.. 32Bit 1kSps..500 MSps
32 Bit 1MSps LTC2508 $16, 24 Bit 2MSps LTC2380 $54, 20 Bit 1.6 MSps MX11905 $30 8 Bit 500MSps ISLA118P5 Intersil $50, 8 Bit 3MSps MAX 11116 $2
Sigma Delta ADC(Results: 1928): 24 Bit 256kSps Range: 8..32 Bit , 3Sps..3.2GSps
16 Bit 3.2GSps(100MHz) AD6676 ADI $200, 16 Bit 160MSps(2.5MHz) AD9262 ADI $48, 12 Bit 3.3kSps ADS1015 TI $2, 32Bit 1MSps LTC2508 $17
Dual Slope (Results: 28): 15 Bit 30Sps
AD conversion signal chain
Analog signal|
Preamplifier (range adjustment, impedance matching) Anti-alising filter Sampling Quantization Digital coding (error correction, filter) |
 |
Zählverfahren, Dual-Slope-Verfahren
|
Version 4
SHEET 1 888 680
WIRE 288 -32 -400 -32
WIRE -208 32 -224 32
WIRE -96 32 -144 32
WIRE -400 128 -400 -32
WIRE 48 128 32 128
WIRE 96 128 48 128
WIRE 160 128 160 80
WIRE -432 144 -448 144
WIRE -176 144 -176 112
WIRE 96 144 96 128
WIRE 128 144 96 144
WIRE -320 160 -352 160
WIRE -224 160 -224 32
WIRE -224 160 -240 160
WIRE -208 160 -224 160
WIRE 288 160 288 -32
WIRE 288 160 192 160
WIRE -432 176 -496 176
WIRE -96 176 -96 32
WIRE -96 176 -144 176
WIRE -48 176 -96 176
WIRE -32 176 -48 176
WIRE 96 176 48 176
WIRE 128 176 96 176
WIRE -208 192 -224 192
WIRE 160 224 160 192
WIRE -176 240 -176 208
WIRE -224 256 -224 192
WIRE -224 256 -288 256
WIRE -352 304 -352 160
WIRE 96 320 96 176
WIRE 128 320 96 320
WIRE 288 320 288 160
WIRE 288 320 208 320
WIRE -352 400 -352 384
FLAG 160 80 Vp
FLAG 160 224 Vn
FLAG 288 160 V2
FLAG -176 112 Vp
FLAG -176 240 Vn
FLAG -48 176 V1
FLAG -496 176 Vin
FLAG -448 144 Vref
FLAG -288 256 Vhalf
FLAG 48 128 Vhalf
FLAG -352 400 0
FLAG -224 32 V3
SYMBOL res 64 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 1k
SYMBOL res 224 304 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R3
SYMATTR Value 10k
SYMBOL cap -144 16 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C1
SYMATTR Value 10�
SYMBOL res -224 144 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL OpAmpX -176 176 R0
SYMATTR InstName X1
SYMBOL OpAmpX 160 160 R0
SYMATTR InstName X2
SYMBOL Switch2 -400 160 R0
SYMATTR InstName X3
SYMBOL res -368 288 R0
SYMATTR InstName R4
SYMATTR Value 10k
TEXT -632 -32 Left 2 !Vp Vp 0 15\nVn Vn 0 0\nVhalf Vhalf 0 DC 7.5\nVref Vref 0 DC 15\nVin Vin 0 DC {Vin}\nVDD VDD 0 15
TEXT -56 56 Left 2 !.tran 0 50m 0
TEXT -224 304 Left 2 !.ic V(v1)=7 V(v3)=7
TEXT -64 88 Left 2 !.global VP VN VDD
TEXT -632 -96 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=500u VT0=1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)\n.model CD4007P PMOS(LEVEL=1 KP=500u VT0=-1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)
TEXT -648 232 Left 2 !.step param Vin LIST 2 4 6\n;.param Vin 7
TEXT -200 368 Left 2 !.meas tran t2 when V(v2)= 3 rise=2\n.meas tran t1 when V(v2)= 3 rise=3\n.meas trab td PARAM t1-t2
|
C = \frac{Q}{U} = \frac{I dt}{dU} = \frac{\frac{U_{in}}{R} dt}{dU}
t_1 = \frac{C dU R}{U_{in}}
t_2 = \frac{C dU R}{U_{ref}}
\frac{t_2}{t_1} = \frac{U_{in}}{U_{ref}}
U_{in} = \frac{t_2}{t_1} U_{ref}
Eine Kapazität C im Integrator wird abwechselnd mit Vin geladen und mit Vref entladen.
Je nach Höhe der Spannung Vin ändert sich die Zeitdauer für einen Lade- Entladevorgang.
Ein Zähler kann diese Zeit messen.
Dieses Verfahren wird bei Multimetern verwendet.
Wie gross ist der Eingangsspannungsbereich?
| Vin in V | 1 | 2 | 3 | 4 | 5 | 6 |
| t1 in ms | 3.85953 | 4.23152 | 4.76959 | 5.61642 | 7.14093 | 10.7025 |
Flash ADC
OperationResolution BSpeedPower |
Version 4 SHEET 1 1480 708 WIRE 736 -784 608 -784 WIRE 784 -784 736 -784 WIRE 880 -784 784 -784 WIRE 608 -768 608 -784 WIRE 608 -672 608 -688 WIRE 912 -672 608 -672 WIRE 992 -672 976 -672 WIRE 736 -624 736 -704 WIRE 912 -624 736 -624 WIRE 992 -624 976 -624 WIRE 160 -576 160 -704 WIRE 640 -576 512 -576 WIRE 784 -576 640 -576 WIRE 880 -576 880 -704 WIRE 912 -576 880 -576 WIRE 992 -576 976 -576 WIRE 608 -560 608 -672 WIRE 608 -560 576 -560 WIRE 736 -560 736 -624 WIRE 736 -560 704 -560 WIRE 880 -560 880 -576 WIRE 880 -560 832 -560 WIRE 240 -512 240 -688 WIRE 256 -512 240 -512 WIRE 384 -512 368 -512 WIRE 512 -512 512 -576 WIRE 512 -512 384 -512 WIRE 592 -512 576 -512 WIRE 864 -512 832 -512 WIRE 368 -496 368 -512 WIRE 368 -496 320 -496 WIRE 160 -480 160 -496 WIRE 256 -480 160 -480 WIRE 512 -480 512 -512 WIRE 528 -480 512 -480 WIRE 640 -480 640 -576 WIRE 656 -480 640 -480 WIRE 784 -480 784 -576 WIRE 592 -464 592 -512 WIRE 592 -464 576 -464 WIRE 864 -464 864 -512 WIRE 864 -464 832 -464 WIRE 160 -448 160 -480 WIRE 576 -448 576 -464 WIRE 704 -448 704 -464 WIRE 832 -448 832 -464 WIRE 528 -416 512 -416 WIRE 640 -416 528 -416 WIRE 608 -400 608 -560 WIRE 608 -400 576 -400 WIRE 736 -400 736 -560 WIRE 736 -400 704 -400 WIRE 368 -384 368 -496 WIRE 384 -384 368 -384 WIRE 240 -368 240 -512 WIRE 256 -368 240 -368 WIRE 512 -368 512 -416 WIRE 512 -368 464 -368 WIRE 368 -352 320 -352 WIRE 400 -352 368 -352 WIRE 592 -352 576 -352 WIRE 160 -336 160 -368 WIRE 256 -336 160 -336 WIRE 512 -320 512 -368 WIRE 528 -320 512 -320 WIRE 640 -320 640 -416 WIRE 656 -320 640 -320 WIRE 160 -304 160 -336 WIRE 592 -304 592 -352 WIRE 592 -304 576 -304 WIRE 576 -288 576 -304 WIRE 704 -288 704 -304 WIRE 528 -256 512 -256 WIRE 640 -256 528 -256 WIRE 608 -240 608 -400 WIRE 608 -240 576 -240 WIRE 880 -240 880 -560 WIRE 880 -240 816 -240 WIRE 368 -224 368 -352 WIRE 384 -224 368 -224 WIRE 240 -208 240 -368 WIRE 256 -208 240 -208 WIRE 512 -208 512 -256 WIRE 512 -208 464 -208 WIRE 368 -192 320 -192 WIRE 400 -192 368 -192 WIRE 592 -192 576 -192 WIRE 864 -192 816 -192 WIRE 160 -176 160 -224 WIRE 256 -176 160 -176 WIRE 160 -160 160 -176 WIRE 512 -160 512 -208 WIRE 528 -160 512 -160 WIRE 640 -160 640 -256 WIRE 768 -160 640 -160 WIRE 592 -144 592 -192 WIRE 592 -144 576 -144 WIRE 864 -144 864 -192 WIRE 864 -144 816 -144 WIRE 576 -128 576 -144 WIRE 816 -128 816 -144 WIRE 368 -96 368 -192 WIRE 384 -96 368 -96 WIRE 608 -96 608 -240 WIRE 608 -96 576 -96 WIRE 240 -80 240 -208 WIRE 256 -80 240 -80 WIRE 512 -80 464 -80 WIRE 368 -64 320 -64 WIRE 400 -64 368 -64 WIRE 160 -48 160 -80 WIRE 256 -48 160 -48 WIRE 592 -48 576 -48 WIRE 160 -32 160 -48 WIRE 512 -16 512 -80 WIRE 528 -16 512 -16 WIRE 592 0 592 -48 WIRE 592 0 576 0 WIRE 576 16 576 0 WIRE 368 32 368 -64 WIRE 384 32 368 32 WIRE 544 48 464 48 WIRE 640 48 544 48 WIRE 768 48 640 48 WIRE 880 48 880 -240 WIRE 880 48 816 48 WIRE 240 64 240 -80 WIRE 256 64 240 64 WIRE 400 64 368 64 WIRE 736 64 736 -400 WIRE 736 64 688 64 WIRE 368 80 368 64 WIRE 368 80 320 80 WIRE 160 96 160 48 WIRE 256 96 160 96 WIRE 848 96 816 96 WIRE 720 112 688 112 WIRE 768 128 768 48 WIRE 640 144 640 48 WIRE 848 144 848 96 WIRE 848 144 816 144 WIRE 720 160 720 112 WIRE 720 160 688 160 WIRE 688 176 688 160 WIRE 816 176 816 144 WIRE 368 208 368 80 WIRE 384 208 368 208 WIRE 736 208 736 64 WIRE 736 208 688 208 WIRE 240 224 240 64 WIRE 256 224 240 224 WIRE 560 224 464 224 WIRE 640 224 560 224 WIRE 368 240 320 240 WIRE 400 240 368 240 WIRE 160 256 160 176 WIRE 256 256 160 256 WIRE 720 256 688 256 WIRE 880 272 880 48 WIRE 880 272 816 272 WIRE 640 288 640 224 WIRE 720 304 720 256 WIRE 720 304 688 304 WIRE 688 320 688 304 WIRE 848 320 816 320 WIRE 368 336 368 240 WIRE 384 336 368 336 WIRE 240 352 240 224 WIRE 256 352 240 352 WIRE 576 352 464 352 WIRE 768 352 576 352 WIRE 368 368 320 368 WIRE 400 368 368 368 WIRE 848 368 848 320 WIRE 848 368 816 368 WIRE 160 384 160 336 WIRE 256 384 160 384 WIRE 160 400 160 384 WIRE 816 400 816 368 WIRE 160 496 160 480 FLAG 160 -704 Vref FLAG 688 176 0 FLAG 688 320 0 FLAG 816 176 0 FLAG 160 496 0 FLAG 992 -576 D0 IOPIN 992 -576 Out FLAG 992 -624 D1 IOPIN 992 -624 Out FLAG 816 400 0 FLAG 784 -784 VDD FLAG 240 -688 Vin IOPIN 240 -688 In FLAG 992 -672 D2 IOPIN 992 -672 Out FLAG 576 16 0 FLAG 576 -128 0 FLAG 816 -128 0 FLAG 576 -288 0 FLAG 704 -288 0 FLAG 576 -448 0 FLAG 704 -448 0 FLAG 832 -448 0 FLAG 368 240 c1 FLAG 368 64 C2 FLAG 368 -64 C3 FLAG 368 -192 C4 FLAG 384 -512 C6 FLAG 368 -352 C5 FLAG 368 368 C0 FLAG 576 352 B0 FLAG 560 224 B1 FLAG 544 48 B2 FLAG 512 -80 B3 FLAG 528 -256 B4 FLAG 528 -416 B5 SYMBOL res 144 -48 R0 SYMATTR InstName R1 SYMATTR Value 4k SYMBOL res 144 80 R0 SYMATTR InstName R2 SYMATTR Value 4k SYMBOL res 144 240 R0 SYMATTR InstName R4 SYMATTR Value 4k SYMBOL res 144 384 R0 SYMATTR InstName R6 SYMATTR Value 4k SYMBOL res 720 -800 R0 SYMATTR InstName R3 SYMATTR Value 100k SYMBOL res 864 -800 R0 SYMATTR InstName R5 SYMATTR Value 100k SYMBOL NOTAND2 432 352 R0 SYMATTR InstName X1 SYMBOL NOTAND2 432 224 R0 SYMATTR InstName X2 SYMBOL NOTAND2 432 48 R0 SYMATTR InstName X3 SYMBOL res 592 -784 R0 SYMATTR InstName R7 SYMATTR Value 100k SYMBOL NOTAND2 432 -80 R0 SYMATTR InstName X4 SYMBOL res 144 -176 R0 SYMATTR InstName R8 SYMATTR Value 4k SYMBOL res 144 -320 R0 SYMATTR InstName R9 SYMATTR Value 4k SYMBOL res 144 -464 R0 SYMATTR InstName R10 SYMATTR Value 4k SYMBOL NOTAND2 432 -208 R0 SYMATTR InstName X5 SYMBOL NOTAND2 432 -368 R0 SYMATTR InstName X6 SYMBOL nmos4 528 -560 R0 SYMATTR InstName M10 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 656 -560 R0 SYMATTR InstName M1 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 784 -560 R0 SYMATTR InstName M2 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 528 -400 R0 SYMATTR InstName M3 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 656 -400 R0 SYMATTR InstName M4 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 768 -240 R0 SYMATTR InstName M5 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 528 -240 R0 SYMATTR InstName M7 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 528 -96 R0 SYMATTR InstName M8 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 640 64 R0 SYMATTR InstName M9 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 768 48 R0 SYMATTR InstName M11 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL nmos4 640 208 R0 SYMATTR InstName M12 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL OpampReal 288 -496 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X7 SYMBOL OpampReal 288 -352 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X8 SYMBOL OpampReal 288 -192 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X9 SYMBOL OpampReal 288 -64 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X10 SYMBOL OpampReal 288 80 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X11 SYMBOL OpampReal 288 240 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X12 SYMBOL OpampReal 288 368 R0 WINDOW 0 32 -40 Bottom 2 SYMATTR InstName X13 SYMBOL nmos4 768 272 R0 SYMATTR InstName M6 SYMATTR Value N SYMATTR Value2 l=0.05u w=0.2u SYMBOL res 144 -592 R0 SYMATTR InstName R11 SYMATTR Value 4k SYMBOL INVx 944 -576 R0 SYMATTR InstName X15 SYMBOL INVx 944 -672 R0 SYMATTR InstName X14 SYMBOL INVx 944 -624 R0 SYMATTR InstName X16 TEXT 336 488 Left 2 !.include cmosedu_models.txt\n.include opamp.sub\n.global VDD\nVDD VDD 0 DC 1.0\nVref Vref 0 DC 0.8\nV1 Vin 0 PULSE(0 1.0 0 50m 50m 0 100m) TEXT 424 -616 Left 2 !.tran 100m TEXT 368 -808 Left 2 ;Thermometer to Binary RECTANGLE Normal 976 432 352 -832 2cmosedu_models.txt |
The Flash ADC generates a thermometer code.
For each level one comparator is needed. High count of comparators, high input capacitance.
High resolution requires low comparator offset and high gain to generate a full level digital signal.
The offset of a comparator depends on the size of the CMOS input transistors:
Voffset ∝ \frac{1}{\sqrt{W \cdot L}}
Lower noise means higher area and higher input capacitance.
If the requirement for comparator offset is not met or noise is present sparkle codes can happen.
The thermometer code is corrupted having more than one transition from 0 to 1.
The code for the first '01' transition is 'OR'ed with the code of the second '01' transition.
Additional digital circuit can be required.
Comparators can feedback noise to the reference voltage ladder. Capacitive coupling between comparator output and intput.
| Thermometer code | Binary Code | ||||||||
| T6 | T5 | T4 | T3 | T2 | T1 | T0 | B2 | B1 | B0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
For each level one comparator is needed. High count of comparators, high input capacitance.
High resolution requires low comparator offset and high gain to generate a full level digital signal.
| Number of Bits | Maximum Offset | Gain |
| 4 | 0.0625 · Vref | 16 |
| 8 | 0.004 · Vref | 256 |
| 10 | 0.001 · Vref | 1024 |
| 12 | 0.0025 · Vref | 4048 |
The offset of a comparator depends on the size of the CMOS input transistors:
Voffset ∝ \frac{1}{\sqrt{W \cdot L}}
Lower noise means higher area and higher input capacitance.
If the requirement for comparator offset is not met or noise is present sparkle codes can happen.
The thermometer code is corrupted having more than one transition from 0 to 1.
| Correct code: | 000000011111111 | Encoded binary code | 1000 |
| Sparkle code: | 000000010111111 | Encoded binary code | 1110 |
Additional digital circuit can be required.
Comparators can feedback noise to the reference voltage ladder. Capacitive coupling between comparator output and intput.
SAR ADC: Blocks
 |
DAC_R2R_6Bit.asc DAC_R2R_6Bit.asy Register6.asc Register6.asy Sample_and_hold.asc Sample_and_hold.asy CMP.asc CMP.asy SAR_CTRL_6bit.asc SAR_CTRL_6bit.asy Version 4 SHEET 1 1360 1288 WIRE 784 -880 752 -880 WIRE 672 -784 640 -784 WIRE 944 -784 928 -784 WIRE 944 -720 944 -784 WIRE 960 -720 944 -720 WIRE 1120 -704 1088 -704 WIRE 960 -688 944 -688 WIRE 784 -672 784 -704 WIRE 784 -672 688 -672 WIRE 1120 -640 1120 -704 WIRE 1120 -640 272 -640 WIRE 496 -592 480 -592 WIRE 816 -592 768 -592 WIRE 768 -576 768 -592 WIRE 944 -576 944 -688 WIRE 512 -560 480 -560 WIRE 816 -560 512 -560 WIRE 528 -528 480 -528 WIRE 816 -528 528 -528 WIRE 288 -512 208 -512 WIRE 944 -512 944 -576 WIRE 944 -512 928 -512 WIRE 544 -496 480 -496 WIRE 816 -496 544 -496 WIRE 272 -480 272 -640 WIRE 288 -480 272 -480 WIRE 560 -464 480 -464 WIRE 816 -464 560 -464 WIRE 288 -448 208 -448 WIRE 576 -432 480 -432 WIRE 816 -432 576 -432 WIRE 592 -400 480 -400 WIRE 640 -368 480 -368 WIRE 688 -368 688 -672 WIRE 688 -368 640 -368 WIRE 496 -336 496 -592 WIRE 816 -336 496 -336 WIRE 816 -304 688 -304 WIRE 1008 -288 944 -288 WIRE 512 -272 512 -560 WIRE 736 -272 512 -272 WIRE 816 -272 736 -272 WIRE 1008 -256 944 -256 WIRE 528 -240 528 -528 WIRE 720 -240 528 -240 WIRE 816 -240 720 -240 WIRE 1008 -224 944 -224 WIRE 544 -208 544 -496 WIRE 736 -208 544 -208 WIRE 816 -208 736 -208 WIRE 1008 -192 944 -192 WIRE 560 -176 560 -464 WIRE 720 -176 560 -176 WIRE 816 -176 720 -176 WIRE 1008 -160 944 -160 WIRE 576 -144 576 -432 WIRE 736 -144 576 -144 WIRE 816 -144 736 -144 WIRE 1008 -128 944 -128 WIRE 592 -112 592 -400 WIRE 720 -112 592 -112 WIRE 816 -112 720 -112 WIRE 768 -80 752 -80 WIRE 816 -80 768 -80 FLAG 640 -784 IN FLAG 944 -576 OUT FLAG 768 -576 0 FLAG 736 -272 Q0 FLAG 720 -240 Q1 FLAG 736 -208 Q2 FLAG 720 -176 Q3 FLAG 736 -144 Q4 FLAG 720 -112 Q5 FLAG 768 -80 RSTb FLAG 1008 -288 X0 FLAG 1008 -256 X1 FLAG 1008 -224 X2 FLAG 1008 -192 X3 FLAG 1008 -160 X4 FLAG 1008 -128 X5 FLAG 752 -880 VDD FLAG 208 -448 RSTb FLAG 688 -304 CLK FLAG 208 -512 CLK FLAG 1120 -704 CMP FLAG 640 -368 sample FLAG 944 -784 INX SYMBOL CMP 1024 -704 M180 SYMATTR InstName X7 SYMBOL DAC_R2R_6Bit 864 -512 R0 SYMATTR InstName X1 SYMBOL Register6 880 -208 R0 SYMATTR InstName X8 SYMBOL Sample_and_hold 688 -720 R0 SYMATTR InstName X9 SYMBOL SAR_CTRL_6bit 384 -480 R0 SYMATTR InstName X2 TEXT 80 -912 Left 2 !.include cmosedu_models.txt\n.global VDD CE\nVDD VDD 0 DC 1\nVCLK CLK 0 PULSE(0 1 0n 1n 1n 8n 20n)\nVCLK1 CLK1 0 PULSE(0 1 0n 1n 1n 8n 20n)\nVCE CE 0 DC 1\nVCLR RSTb 0 PULSE(1 0 5n 1n 1n 28n 280000n)\nVIn IN 0 PULSE(0 1 0n 4000n 4000n 400n 8400n) TEXT 304 -96 Left 2 !.tran 4000n TEXT 224 -32 Left 2 ;4000ns Ramp of V(In), 20ns CLK rate 50MHz, 50nm models, 120ns conversion 5 Bits TEXT 976 -400 Left 2 ;DAC TEXT 976 -752 Left 2 ;CMP TEXT 960 -360 Left 2 ;Output\nBuffer TEXT 808 -888 Left 2 ;Sample and Hold |
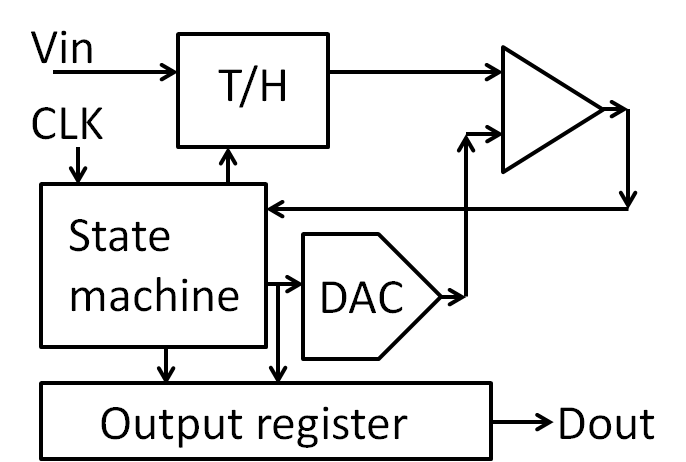At the beginning of the conversion an input signal is sampled.
The comparator compares it with the output of the DAC.
The state machine sets the MSB depending on the outcome of the comparison and then tries the next bit.
The comparator compares it with the output of the DAC.
The state machine sets the MSB depending on the outcome of the comparison and then tries the next bit.
SAR ADC: Flow, Algorithm, Simulation
|
Vref = 1V Vin = 0.6 V Stellen Sie den zeitlichen Verlauf der internen Vergleichsspannung Vout des SAR ADC dar. |
Input: 0.6
1 * 0.5 + 0 * 0.25 + 0 * 0.125 + 1 * 0.0625 + 1 * 0.03125 + 0 * 0.015625 + 0 * 0.0078125 + 1 * 0.00390625
0.59765625
SAR ADC: Flow, Algorithm, Simulation
|
Set MSB to 1: 100000 Loop until LSB set: Compare DAC output with analog input: If DAC output > analog input reset current bit. Try and set next bit. End Loop Blue line shows analog input voltage. Green shows output of internal DAC. Red shows output code with MSB first. |
1 * 0.5 + 0 * 0.25 + 0 * 0.125 + 1 * 0.0625 + 1 * 0.03125 + 0 * 0.015625 + 0 * 0.0078125 + 1 * 0.00390625
0.59765625
SAR ADC: Benefits and Challenges
- Separate blocks can be optimized individually
- Comparator gain and offset:
LSB * gain = Vref
Voffset < LSB
ΔV << LSB: Metastability - Conversion time: n-bits * Settling time
tconv= n * tsettle
Mittelwertbildung
Mittelwertbildung Formel: y[i] = (x[2 * i] + x[2 * i +1]) / 2|
Der Wertebereich verdoppelt sich. Das Signal-Rausch Verhältnis ändert sich, da nur noch halb so viele FFT Frequenzen zur Verfügung stehen. 20 log \left( \sqrt{2} \right) = 10 log \left( 2 \right) = 3 dB Das letzte Bit hat einen Rauschanteil. |
Man kann auch von einer Oversamplingrate OSR von 2 sprechen.
Der Signal-Rausch-Abstand erhöht sich bei Mittelwertbildung mit OSR Werten um:
10 log \left( OSR \right)
Die Grafik zeigt ein Sinussignal mit einer Amplitude von Ua = 128 und einer Auflösung von 8 Bit und eine Mittelwertbildung.
Der Effektivwert ergibt sich bei einer Sinusspannung mit dem Faktor \sqrt{2} .
A_{signal} = 20 \cdot log_{10}(\frac{Ua}{\sqrt{2}})
A_{signal} = 20 \cdot log_{10}(\frac{128}{\sqrt{2}}) = 39 dB
Man erwartet ein SQNR = 6.02 * 8 dB + 1.76 dB = 49.78 dB
Das wäre ein Rauschpegel von - 10.78 dB (Grüne Linie).
Dieses Rauschen wird auf alle dargestellten Frequenzen (128 = 256 / 2 = NFFT / 2 ) aufgeteilt.
v_{Ges} = \sqrt{N \cdot v_i^2 }
dA_{NFFT} = 20 \cdot log_{10} \left(\sqrt{\frac{NFFT}{2}}\right) = 10 \cdot log_{10}\left(\frac{NFFT}{2}\right) = 21 dB
Das Rauschen der einzelnen Frequenzen liegt dann in etwa bei -31 dB (Rote Kurve).
Bei der logarithmischen Darstellung der Frequenz liegen die Punkte der höheren Frequenzen dichter zusammen. In der Darstellung sieht man eine starke Schwankung der einzelnen Werte.
Eine Ablesung des Signal-Rausch Verhältnisses aus der Graphik ist deshalb nicht sinnvoll.
Der Signal-Rausch Abstand muss numerisch berechnet werden.
Oversampling ADC: History
Nyquist ADCOversamplingfCLK = OSR · 2 · fbw Clock frequency is much higher than bandwidth. Pulse count Modulation (PCM)Predictive CodingQuantize difference of the signal Sigma delta converter |
 |
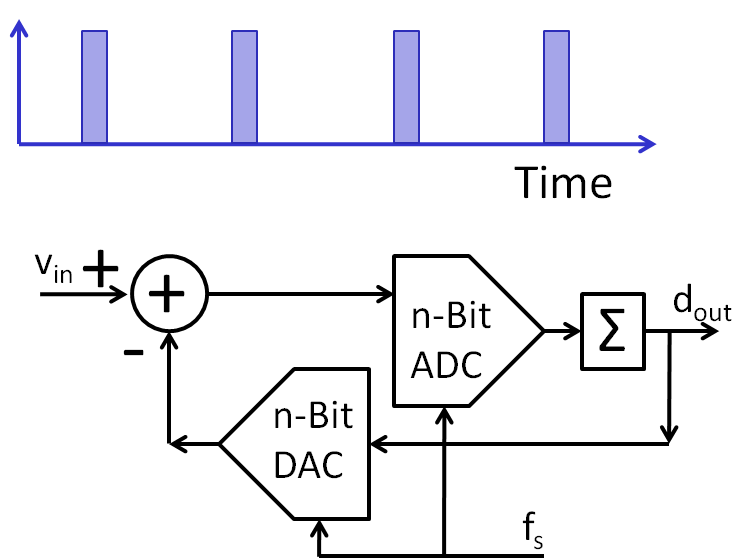Sigma Delta ADC Architectures
 |
   |
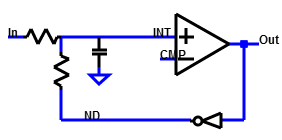First order passive Sigma Delta Modulator
Version 4 SHEET 1 1168 680 WIRE 0 128 -32 128 WIRE 160 128 80 128 WIRE 272 128 160 128 WIRE 320 128 272 128 WIRE 464 144 432 144 WIRE 496 144 464 144 WIRE 80 160 80 128 WIRE 320 176 288 176 WIRE 160 208 160 192 WIRE 80 304 80 240 WIRE 128 304 80 304 WIRE 352 304 128 304 WIRE 464 304 464 144 WIRE 464 304 416 304 FLAG -32 128 In IOPIN -32 128 In FLAG 496 144 Out FLAG 272 128 INT FLAG 128 304 ND FLAG 288 176 CMP FLAG 160 208 0 SYMBOL Diffamp 384 144 R0 SYMATTR InstName X3 SYMBOL cap 144 128 R0 SYMATTR InstName C1 SYMATTR Value 10p SYMBOL res 64 144 R0 SYMATTR InstName R1 SYMATTR Value 200k SYMBOL res 96 112 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R2 SYMATTR Value 200k SYMBOL INVx 384 304 M0 SYMATTR InstName X1 TEXT 560 48 Left 2 !.global VDD CE RSTb CLK\nVCLK CLK 0 PULSE(0 1 0 0.1n 0.1n 100n 200n)\nVIN IN 0 SINE( 0.55 0.4 5798.33984375)\n*VIN IN 0 DC 0.45\nVDD VDD 0 DC 1\nVCMP CMP 0 DC 0.5\nVRST RSTb 0 DC 1\nVCE CE 0 DC 1\n.tran 0 3.2808m 4u\n* 100ns * 4 * 4096 (punkte fft) = 3.2768ms trans\n* 19 Perioden => 1/3.2768m*19 = 5798.33984375 TEXT -72 64 Left 2 !.include cmosedu_models.txt TEXT -88 328 Left 2 !.options plotwinsize=0
Internal voltage levels:The voltage V(INT n+1) at clock cycle n+1 is:V_{int n+1} = V_{int n} + \frac{\delta t}{C} \left( \frac{ V_{not(Dout)} - V_{int n}}{R} + \frac{V_{in} - V_{int n}}{R} \right) V_{int n+1} = V_{int n} + \frac{\delta t}{C \cdot R} \left( V_{not(Dout)} + V_{in} - 2 \cdot V_{int n} \right) \delta t is the period of the clock. V_{Dout} in a real logic circuit is 0V or VDD. These equations are used for a high level simulation. High level simulation: 1st order sigma delta simulation Since Vint has to stay between 0V and VDD: \frac{\delta t}{C \cdot R} 2 V_{DD} \lt V_{DD} C \cdot R \gt \frac{2}{f_{sample} } \frac{1}{C \cdot R} \lt \frac{f_{sample} }{2} The bandwidth limit of RC has to be smaller than fsample/2. The bandwidth limit of RC has to be greater than the interested bandwith. fsample/2/OSR 2 \pi f_{bw} \lt \frac{1}{C \cdot R} \lt \frac{f_{sample} }{2} |
On the left the difference of V(in) and V(D) is integrated and then
compared with V(CMP). The comparator operates with the clock frequency and
gives for each clock cycle a new value.
A simple passive first order sigma delta converter uses resistors and capacitances.
This circuit is according to Baker, "CMOS integrated cicuits", Figure 6.4
A simple passive first order sigma delta converter uses resistors and capacitances.
This circuit is according to Baker, "CMOS integrated cicuits", Figure 6.4
Schalter und Sample and Hold
|
Version 4 SHEET 1 880 680 WIRE 224 16 224 0 WIRE -32 64 -48 64 WIRE 0 64 -32 64 WIRE 192 64 80 64 WIRE 288 64 256 64 WIRE 400 64 288 64 WIRE 512 80 464 80 WIRE 560 80 512 80 WIRE 576 80 560 80 WIRE 288 96 288 64 WIRE 400 96 352 96 WIRE 352 160 352 96 WIRE 512 160 512 80 WIRE 512 160 352 160 WIRE 288 208 288 160 FLAG 288 208 0 FLAG 224 0 CLK FLAG -32 64 IN FLAG 288 64 OUT FLAG 560 80 OUTB SYMBOL res 96 48 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R1 SYMATTR Value 4 SYMBOL Switch 224 64 R0 SYMATTR InstName X1 SYMBOL cap 272 96 R0 SYMATTR InstName C1 SYMATTR Value 5n SYMBOL OpAmpModel 432 80 M180 SYMATTR InstName X2 TEXT -104 -224 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u \n+ VT0=0.5 LAMBDA=0.018\n+ CGDO = 200E-10 CGSO=200E-10 CGBO=1E-8)\n.model CD4007P PMOS(LEVEL=1 KP=1123u \n+ VT0=-0.5 LAMBDA=0.018\n+ CGD0 = 200E-12 CGS0=200E-12 CGB0=1E-10) TEXT -88 256 Left 2 !V0 CLK 0 PULSE(5 0 0n 1n 1n 199n 400n) TEXT 96 120 Left 2 !.tran 1600n TEXT -80 288 Left 2 !*V1 IN 0 DC 2 \nV1 IN 0 PULSE(0 5 100n 1n 1n 800n) |
Vergleich der Wandlerprinzipien
Dual-slope Verfahren
Flash ADC
SAR ADC
Sigma Delta ADC
Zusammenfassung und nächste Vorlesung
- Übersicht
- Dual Slope
- Flash
- SAR
- Sigma Delta Wandler
Nächstes Mal