Grundlagen Elektrotechnik 2 (GET2)

03 Sinusförmige Wechselgrößen

Prof. Dr. Jörg Vollrath

02 Wechselgrößen GET 2

Material: Diodenschaltung, (Leiterschleife)

Rückblick und Übersicht

Mittelwerte: Gleichwert und Effektivwert
Analytische Gleichung (Geradengleichung
Integration und numerische Integration
Simulation
Gleichrichtwert

Sinusförmige Wechselgrößen: Effektivwert
Leiterschleife
Überlagerung: Rechtecksignal, Schwebung

Wer hat sich schon die Webseiten angeschaut?
Was finden Sie gut? Was erwarten Sie?

Rechnung Effektivwert einer Mischgröße

$u(t) = u_0 + \hat{u}_1 \cdot sin \left( \omega t \right)$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt }$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T (u_0 + \hat{u}_1 \cdot sin \left( \omega t \right))^2 dt }$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T (u_0^2 + \hat{u}_1^2 \cdot sin^2 \left( \omega t \right) + 2 \cdot u_0 \cdot \hat{u}_1 \cdot sin \left( \omega t \right)) dt }$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T (u_0^2) dt + \frac{1}{T} \int_0^T (\hat{u}_1^2 \cdot sin^2 \left( \omega t \right)) dt }$
mit:

$\int_0^T ( 2 \cdot u_0 \cdot \hat{u}_1 \cdot sin \left( \omega t \right)) dt = 0$

$U_{eff} = \sqrt{u_{0eff}^2 + u_{1eff}^2 }$

Gleichrichtwert

Gleichrichterschaltung (rectifier circuit)
Der Strom fliesst nur in eine Richtung
Diodenfunktion: Ideale Diode
$U_D > 0, R_D = 0$ leitet
$U_D < 0, R_D = \infty$ sperrt
Einweggleichrichterschaltung (half wave rectifier circuit)
$u_{E}(t) = \cases{ u(t) & \text{für} u(t) \gt 0 \cr 0 & \text{für} u(t) \lt 0 }$
Brückengleichrichter
$u_{Br} = | u(t) |$

EinwegGleichrichter.asc

Version 4
SHEET 1 880 680
WIRE 32 96 -48 96
WIRE 208 96 96 96
WIRE 208 112 208 96
WIRE -48 128 -48 96
WIRE -48 224 -48 208
WIRE 208 224 208 192
WIRE 208 224 -48 224
WIRE 208 272 208 224
FLAG 208 272 0
FLAG -48 96 U1
FLAG 208 96 UR
SYMBOL voltage -48 112 R0
WINDOW 39 0 0 Left 2
WINDOW 3 24 160 Left 2
SYMATTR Value SINE(0 30 1k)
SYMATTR InstName V1
SYMBOL res 192 96 R0
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL diode 32 80 M90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D1
TEXT 40 176 Left 2 !.tran 4m

BrueckenGleichrichter.asc

Version 4
SHEET 1 880 680
WIRE 96 16 48 16
WIRE 176 16 96 16
WIRE 208 16 176 16
WIRE 48 32 48 16
WIRE 96 64 96 16
WIRE -48 96 -64 96
WIRE 0 96 -48 96
WIRE 0 112 0 96
WIRE 48 112 48 96
WIRE 48 112 0 112
WIRE 208 112 208 16
WIRE -64 128 -64 96
WIRE 96 144 96 128
WIRE 96 144 0 144
WIRE 48 160 48 112
WIRE 96 160 96 144
WIRE -64 224 -64 208
WIRE 0 224 0 144
WIRE 0 224 -64 224
WIRE -64 240 -64 224
WIRE 48 240 48 224
WIRE 96 240 96 224
WIRE 96 240 48 240
WIRE 176 240 96 240
WIRE 208 240 208 192
WIRE 208 240 176 240
FLAG -64 240 0
FLAG 176 16 URH
FLAG 176 240 URL
FLAG -48 96 U1
SYMBOL voltage -64 112 R0
WINDOW 39 0 0 Left 2
WINDOW 3 24 160 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(0 30 1k)
SYMBOL res 192 96 R0
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL diode 80 128 M180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D1
SYMBOL diode 32 96 M180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D2
SYMBOL diode 80 224 M180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D3
SYMBOL diode 32 224 M180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D4
TEXT -64 32 Left 2 !.tran 4m

Motivation Sinusförmige Wechselgröße

Energieerzeugung
Leiterschleife in einem Magnetfeld
Signalübertragung MP3
Jede beschränkte nicht sinusförmige periodische Wechselgröße läßt sich in eine bestimmte unendliche Reihe mit sinusförmigen Summengliedern überführen.

Leiterschleife im Magnetfeld

Die Fläche der Leiterschleife ist A.
Die magnetische Flussdichte ist B.
Die effektive Fläche der Leiterschleife bei einer Rotation mit der Winkelgeschwindigkeit

$\omega$ zum Zeitpunkt t ist:

$A \cdot \cos( \omega t)$
Der magnetische Fluss

$\Phi(t)$ ist dann:

$\Phi(t) = B \cdot A \cdot \cos( \omega t)$
und die induzierte Spannung u(t) ist:

$U = \frac{\mathrm{d}\Phi}{\mathrm{d}t} = B \cdot A \cdot (-\omega) \cdot \sin(\omega t)$
Die Spannung kann durch eine größere Fläche, höhere Winkelgeschwindigkeit oder grösserer magnetischer Flussdichte erhöht werden.

$\phi$ : 0 °

Rechtecksignal aus Sinusschwingungen

$\sum\limits_n \frac{1}{n} sin( n x)$

$n = 1,3,5,7,..$

Fouriertransformation 3.Semester
Zerlegung einer periodischen Wechselgröße in Sinusgrößen.
Dies wird beispielsweise bei der MP3 Kodierung genutzt.

Sinusförmige Wechselgröße (25.03.2025 05)

$u(t) = \hat{u} sin( \omega t + \phi_0 )$

$u(t) = \hat{u} cos( \omega t + \phi_0 - \frac{\pi}{2})$

$\hat{u}$ : Amplitude

$\omega$ : Kreisfrequenz

$[s^{-1}]$

$\omega = 2 \pi f$

$\phi_0$ : Nullphasenwinkel [°]
Der Nullphasenwinkel wird bei der Oszilloskopdarstellung durch den Trigger eingestellt.

Phasenverschiebungswinkel (phase difference)

$\phi_{12} = \phi_{1} - \phi_{2}$

$\phi_{12} \gt 0$ : Die Schwingung 1 eilt der Schwingung 2 voraus.

$\phi_{12} \lt 0$ : Die Schwingung 1 eilt der Schwingung 2 nach.

Beim Oszilloskop liest man den Phasenwinkel aus einer Zeitdifferenz der Nulldurchgänge ab.
t₁ und t₂ seien die Zeitpunkte Nulldurchgänge der Kurven 1 und 2. T sei die Periodendauer der Signale. Eine Periode T entspricht einem Winkel von 2 π.

$\phi_{12} = \frac{t_1-t_2}{T} 2 \pi$

Gleichwert, Gleichrichtwert und Effektivwert einer sinusförmigen Wechselgröße

$u(t) = \hat{u} sin( \omega t + \phi_0 )$

Gleichwert:

$\overline{u} = \frac{1}{T} \int\limits_{t_1}^{T + t_1} \hat{u} sin( \omega t + \phi_0) dt$

$\overline{u} = \frac{\hat{u}}{T} \left[ - \frac{1}{\omega} cos( \omega t + \phi_0) \right]_{t_1}^{T + t_1}$

$\overline{u} = - \frac{\hat{u}}{T \cdot \omega} \left( cos( \omega (T + t_1) + \phi_0) - cos( \omega t_1 + \phi_0) \right) = 0$

Gleichrichtwert:

$| \overline{u} | = \frac{2}{T} \int\limits_{0}^{\frac{T}{2}} \hat{u} sin( \omega t ) dt$

$\overline{u} = \frac{2 \hat{u}}{T} \left[ - \frac{1}{\omega} cos( \omega t ) \right]_{0}^{\frac{T}{2}}$

$\overline{u} = - \frac{2 \hat{u}}{T \cdot \omega} \left( cos( \omega \frac{T}{2} ) - cos( \omega \cdot 0) \right) = \frac{4 \hat{u}}{T \cdot \omega}$

$\overline{u} = \frac{4 \hat{u}}{T \cdot 2 \cdot \pi f} = \frac{2 \hat{u}}{\pi} = 0.637 \hat{u}$

Effektivwert:

$U = \sqrt{ \frac{1}{T} \int\limits_{0}^{T} \hat{u}^2 sin^2( \omega t ) dt }$

$U = \sqrt{ \frac{ \hat{u}^2}{T} \left[ \frac{t}{2} - \frac{1}{4 \cdot \omega} sin( 2 \omega t ) \right]_{0}^{T} }$

$U = \sqrt{\frac{ \hat{u}^2}{T} \left( \frac{T}{2} - \frac{1}{4 \cdot \omega} sin( 2 \omega T ) - \frac{0}{2} + \frac{1}{4 \cdot \omega} sin( 2 \omega 0 ) \right) }$

$U = \sqrt{ \frac{ \hat{u}^2}{T} \left( \frac{T}{2} \right)} = \frac{\hat{u}}{\sqrt{2}} = 0.707 \hat{u}$

Feedback: Gerade, Integral (26.03.2024)

Schreiben Sie selbstständig mit
Warum konnten Sie die vorgestellte Integraldarstellung nicht direkt anwenden?
Geradengleichung: Kästchen x-Achse 1s, y-Achse 0.5V
4 Kästchen x, 4 Kästchen y ergeben: 2V/4s = 0.5 V/s
Einheiten in der Geradengleichung
Weniger verrechnet
Lösung: 4..11 min
1. Übungsblatt

Test Geradengleichung und Integral (2025)

Aufgabe	Richtig	Gesamt
Geradengleichung
Umrechnung 0.02 V/ms in V/s
Integralrechnung
Nicht Verrechnet

Test Effektivwert 3 (2025)

Aufgabe	Richtig	Gesamt
Periode
Frequenz
Gleichanteil
Amplitude
Effektivwert

Test Geradengleichung 2

Frage	2024
Frage	Richtig	Gesamt
Geradengleichung	18	21
Integral	15	21

Fragen

Welche praktische Bedeutung hat die Überlagerung von sinusförmigen Wechselgrößen?
Was passiert bei der Überlagerung von sinusförmigen Wechselgrößen gleicher Frequenz?
Was passiert bei der Überlagerung von sinusförmigen Wechselgrößen unterschiedlicher Frequenz?

Integrieren Sie folgenden Term von 2 s bis 4 s.

u(t) = 3 V + 0.02 V/ms t + 3 V s^-2 t²

Geradengleichung:
Die Steigung ist dy / dx.

Integralschreibweise: Integral, Stammfunktion mit Grenzen

$\int_{2s}^{4s} 3 V + 0.02 V/ms t + 3 Vs^{-2} t^2 dt = \left[ 3 V t + 0.02 V/ms \frac{t^2}{2} + 3 Vs^{-2} \frac{t^3}{3} \right]_{2s}^{4s}$

$\left( 3 V 4 s + 0.02 V/ms \frac{16 s^2}{2} + 3 Vs^{-2} \frac{64 s^3}{3} \right) - \left( 3 V 2 s + 0.02 V/ms \frac{4 s^2}{2} + 3 Vs^{-2} \frac{8 s^3}{3} \right)$
Vorzeichen und Klammer:

$3 V 4 s + 0.02 V/ms \frac{16 s^2}{2} + 3 Vs^{-2} \frac{64 s^3}{3} - 3 V 2 s - 0.02 V/ms \frac{4 s^2}{2} - 3 Vs^{-2} \frac{8 s^3}{3}$

Einheiten unter dem Bruchstrich:

$12 Vs + 20 Vs \cdot 8 + 64 Vs - 6 Vs - 40 Vs - 8 Vs = 182 Vs$

Integralgrenzen kann man hier nicht verschieben.
Wenn man beim X Wert eine Differenz hat, kann man Integralgrenzen verschieben:

$\int_{2s}^{4s} (x - 2s) dt = \int_{0s}^{2s} x dt$

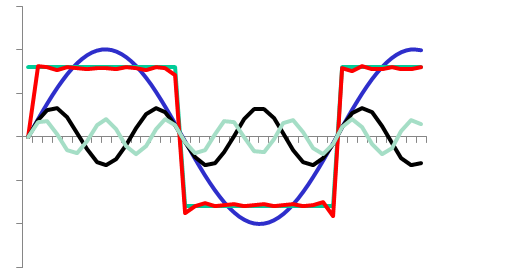
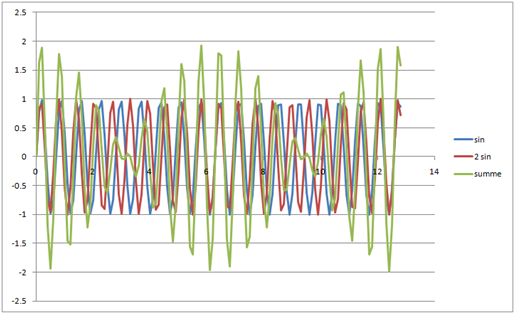
Sinusgrößen unterschiedlicher Frequenz

$u(t) = \hat{u}_1 cos(\omega_1 t + \phi_{u1}) + \hat{u}_2 cos(\omega_2 t + \phi_{u2} )$

Graphische, numerische Lösung

Excel, SPICE

1. Sonderfall:

$T_1 = n T_2$ mit n = 1, 2, 3, ..
Resultierende Periode: $T = T_1$

2. Sonderfall:

Differenz f₁ und f₂ klein: Schwebung (beat)
$\hat{u}_1 = \hat{u}_2$
Mit $\omega = \frac{\omega_1 + \omega_2}{2}$ , $\Delta \omega = \frac{\omega_1 - \omega_2}{2}$
$\phi = \frac{\phi_{u1} + \phi_{u2}}{2}$ , $\Delta \phi = \frac{\phi_{u1} - \phi_{u2}}{2}$
$cos \alpha + cos \beta = 2 cos \frac{\alpha + \beta}{2} cos \frac{\alpha - \beta}{2}$
$u(t) = \hat{u}_1 cos ( \Delta \omega t + \Delta \phi) cos ( \omega t + \phi )$

Überlagerung von Sinusgrößen gleicher Frequenz

$u(t) = u_1 (t) + u_2 (t)$

Darstellung der zu erwartenden Funktion und der Summe der 2 Funktionen:

$u(t) = \hat{u} cos ( \omega t + \phi_u )$	$u(t) = \hat{u}_1 cos ( \omega t + \phi_{u1} ) + \hat{u}_2 cos ( \omega t + \phi_{u2} )$
mit: $cos( \alpha + \beta) = cos \alpha cos \beta - sin \alpha sin \beta$
$u(t) = \hat{u} ( cos \phi_u cos \omega t - sin \phi_u sin \omega t )$ $u(t) = \hat{u} cos \phi_u cos \omega t - \hat{u} sin \phi_u sin \omega t$	$u(t) = \hat{u}_1 ( cos \omega t cos \phi_{u1} - sin \phi_{u1} sin \omega t ) + \hat{u}_2 ( cos \omega t cos \phi_{u2} - sin \phi_{u2} sin \omega t )$ $u(t) = ( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} ) cos \omega t - ( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} ) sin \omega t$

Koeffizientenvergleich für

$sin \omega t$ und

$cos \omega t$ :

(1)

$\hat{u} cos \phi_u = \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}$
(2)

$\hat{u} sin \phi_u = \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}$
Bestimmung des Winkels aus dem Quotienten

$\frac{(2)}{(1)}$ :

$\frac{\hat{u} sin \phi_u}{\hat{u} cos \phi_u} = \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}}$

$\phi_u = arctan \left( \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}} \right)$
Bestimmung der Amplitude aus

$(1)^2 + (2)^2$

$\left( \hat{u} cos \phi_u \right)^{2} + \left( \hat{u} sin \phi_u \right)^{2} = \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2}$

$\hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2} }$

$\hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1}\right)^{2} + \left( \hat{u}_2 cos \phi_{u2} \right)^{2} + 2 \hat{u}_1 cos \phi_{u1} \hat{u}_2 cos \phi_{u2} + \left( \hat{u}_1 sin \phi_{u1} \right)^{2} + \left( \hat{u}_2 sin \phi_{u2} \right)^{2} + 2 \hat{u}_1 sin \phi_{u1} \hat{u}_2 sin \phi_{u2} }$

$sin^{2} \phi + cos^{2} \phi = 1$

$cos \alpha cos \beta + sin \alpha sin \beta = cos ( \alpha - \beta)$

$\hat{u} = \sqrt{ \left( \hat{u}_1 \right)^{2} + \left( \hat{u}_2 \right)^{2} + 2 \hat{u}_1 \hat{u}_2 cos(\phi_{u2} - \phi_{u1}) }$

Beispiel: Überlagerung von Sinusgrößen gleicher Frequenz

Zwei Quellen mit sinusförmiger Quellenspannung gleicher Frequenz sind in Reihe geschaltet.

$\hat{u}_{q1} = 50 V; \phi_{u1} = 80°; f_1 = 50 Hz;$

$\phi = \frac{80°}{180°} \cdot \pi = 1.396$

$\hat{u}_{q2} = 30 V; \phi_{u2} = 15°; f_2 = 50Hz;$

Simulieren Sie mit SPICE und berechnen Sie die Amplitude und den Nullphasenwinkel der Klemmenspannung und zeichnen Sie die Liniendiagramme sämtlicher Spannungen.

$\hat{u} = \sqrt{ \left( \hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2} \right)^{2} + \left( \hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2} \right)^{2} }$

$\hat{u} = \sqrt{ \left( 37.66 V \right)^{2} + \left( 57 V \right)^{2} } = 68.3 V$

$\phi_u = arctan \left( \frac{\hat{u}_1 sin \phi_{u1} + \hat{u}_2 sin \phi_{u2}} {\hat{u}_1 cos \phi_{u1} + \hat{u}_2 cos \phi_{u2}} \right) = 56.55°$

Zusammenfassung und nächstes Mal

Generator, Leiterschleife
Überlagerung von Sinusschwingungen:
Unterschiedliche Frequenzen: Rechteck, Schwebung
Gleiche Frequenz: Änderung der Phase und Amplitude

04 LTSPICE

Ein Wechselspannungsgenerator verhält sich wie eine Leiterschleife im Magnetfeld und erzeugt eine sinusförmige Spanung.

u(t) = u sin( ω t + φ )

$\omega = 2 \pi f = 2 \pi \frac{1}{T}$

u: Spannungsamplitude
ω : Winkelgeschwindigkeit
f: Frequenz
T: Periodendauer
φ: Phasenwinkel

Mit dem Dreisatz kann man den Winkel in Grad in ein Bogenmaß umrechnen

$\frac{40°}{360°} = \frac{1}{9} = \frac{ 2 \pi \frac{1}{9}}{ 2 \pi}$

Eine beliebige Wechselgröße kann man aus Überlagerung von Sinusschwingungen darstellen.
Zur Analyse und Synthese einer beliebigen Wechselgröße wird eine Fouriertransformation verwendet.

2025 GET 2 03 Sinus Prof. Dr. Joerg Vollrath