Grundlagen Elektrotechnik 2 (GET2)

02 Wechselgrößen

Gleichwert, Effektivwert

Prof. Dr. Jörg Vollrath

01 Einführung GET 2

Material: Electronic Explorer, ADALM2000, EEBench, (Diodenschaltung)
Test 03 Geradengleichung, Test 04 Wechselgrößen

Rückblick und Heute

Begriffe der Wechselgrößen

Periodizität, Periodendauer T, Frequenz f
Maximalwert, Amplitude, Scheitelwert û

Mittelwerte:

Gleichwert u: Mittelwert über eine Periode
Effektivwert U: Leistungsmotiviert
Quadrat der Spannung oder des Stroms
Aufpassen bei der Integration

Begriffe: Gleichgröße, Wechselgröße, Mischgröße
Mathematik:
Wie stellt man eine Geradengleichung auf?
y = y₀ + a (x - x₀)
Wie integriert man?

Vorsatzzeichen, Periode, Frequenz

Diskutieren Sie mit ihrem Nachbarn:

Wie wandelt man eine vorsatzzeichenbehaftete Größe in eine wissenschaftliche Darstellung um?
3 ms = 3 · 10^-3 s
Wie wandelt man eine wissenschaftliche Darstellung einer Größe in eine vorsatzzeichenbehaftete Darstellung um?
4000 V = 4 kV
Wie kommt man von einer Frequenz von 1 MHz auf die Periodendauer als vorsatzzeichenbehaftete Zahl?
Stellen sie $0.5 V/ms = 0.5 V/(ms) = 0.5 \frac{V}{ms}$ mit der Einheit V/s dar

Ziele

Ziele für Mittelwerte periodischer Größen:
Sie können:

Begründen, warum zur Beurteilung periodischer Schwingungen Mittelwerte zweckmäßig sind.
Die Definition von Gleichwert, Effektivwert und Gleichrichtwert angeben.
Die Begriffe Gleichanteil und Wechselanteil anhand einer Skizze erläutern.
Die Ersatzschaltungen für eine Mischstromquelle und für eine Mischspannungsquelle angeben
Den Effektivwert eines Stromes physikalisch interpretieren.
Eine Brücken-Gleichrichterschaltung skizzieren

Mittelwerte periodischer Größen

Mittelwerte werden auf eine Periode bezogen.

Gleichwert (direct component, DC)

arithmetischer Mittelwert (mean value)
$\overline{u}= \frac{1}{T} \int_0^T u(t) dt$
Das Integral kann als Fläche unter dem Kurvenverlauf interpretiert werden.
Positive Spannungen und negative Spannungen können sich aufheben, so dass der arithmetische Mittelwert Null wird.
Ist der Mittelwert nicht Null spricht man von einer Mischgröße.

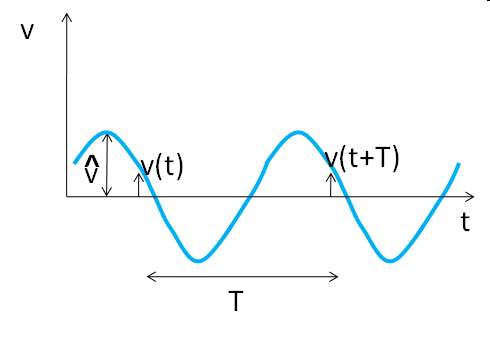
Mittelwerte periodischer Größen

Mittelwerte werden auf eine Periode bezogen.

Effektivwert (root mean square value)

$U = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt}$
Da die zeitabhängige Spannung quadriert wird, trägt auch eine negative Spannung zum Effektivwert bei.
Da die zeitabhängige Spannung quadriert wird, tragen große Absolutwerte viel mehr zum Effektivwert bei als kleine Absolutwerte.

Integralrechnung

Flächeninterpretation
Beschleunigung, Geschwindigkeit, Weg
Umfang, Fläche, Volumen
Differentialgleichungen, Differentialrechnung

Listen, Regeln
Numerische Integration

Beispiel Mischgröße

Berechnen Sie den Gleichwert und den Effektivwert folgender Größe.

Abschnittsweise

Geradengleichung

Integralbildung

Beispiel Mischgröße

Berechnen Sie den Gleichwert und den Effektivwert folgender Größe.

10n,3,1,4,0,1,2,-4,1,-2,0,1,0,0
⇒ Wechselgrößen
Electronic Explorer: Mischgroesse.csv 250 kHz, Amplitude: 3V, Offset 1V

Abschnittsweise Geradengleichung

$u(t) = \cases{ 4 V & \text{ für } \text{0 ns }+ n\cdot T \lt t \lt 10 ns+n\cdot T\cr 2 V -0.4 \frac{V}{ns} \cdot \left( t - 10ns \right) & \text{ für } \text{10 ns }+ n\cdot T \lt t \lt 20 ns+n\cdot T\cr -2 V & \text{ für } \text{20 ns }+ n\cdot T \lt t \lt 30 ns+n\cdot T\cr 0 V & \text{ für } \text{30 ns }+ n\cdot T \lt t \lt 40 ns+n\cdot T\cr }$

Integralbildung mit verschobenen Grenzen

$\overline{U} = \frac{1}{T}\int\limits_{0}^{T} u(t) dt = \frac{1}{T} \left( \int\limits_{0}^{10ns} \left( 4 V \right) dt + \int\limits_{0}^{10ns} \left( 2 V -0.4 \frac{V}{ns} \cdot t \right) dt + \int\limits_{0}^{10ns} \left( -2 V \right) dt + \int\limits_{0}^{10ns} \left( 0 V \right) dt \right)$

$U_{eff} = \sqrt{ \frac{1}{T}\int\limits_{0}^{T} u^2(t) dt } = \sqrt{ \frac{1}{T} \left( \int\limits_{0}^{10ns} \left( 4 V \right)^2 dt + \int\limits_{0}^{10ns} \left( 2 V -0.4 \frac{V}{ns} \cdot t \right)^2 dt + \int\limits_{0}^{10ns} \left( -2 V \right)^2 dt + \int\limits_{0}^{10ns} \left( 0 V \right)^2 dt \right) }$

Ergebnis Test 1 und 2 (19.03.2025)

26 Teilnehmer	Summe	ok	Falsch	Teil/Ansatz	26 Teilnehmer	Summe	ok	Falsch	Teil/Ansatz
Periode	25	20	5	0	Periode	26	23	3	0
Frequenz	23	10	10	3	Frequenz	26	18	6	2
Gleichanteil	15	12	2	1	Gleichanteil	25	20	3	0
Amplitude	23	19	4	0	Amplitude	22	22	0	0
Effektivwert	18	0	16	2	Effektivwert	19	3	7	9

Rechnen mit Vorsatzzeichen in Brüchen ist schwierig
Gleichwert stimmt, aber die Integralrechnung fehlt
Effektivwert als Integralrechnung fehlt
Einheiten sind auch beim Endergebnis nötig.
Sie hatten noch keine iNtegralrechnung?

Strom- und Spannungsformen

Gleichgröße:
$x(t) = const$
Pulsierende Gleichgröße:
Ändert die Richtung nicht
Mischgröße:
Mittelwert $\overline{x} \neq 0$
Überlagerung von Gleichanteil und Wechselanteil
Wechselgröße:
$x(t) = x(t ± n T) n=0,1,2,..$
$\overline{x} = \frac{1}{T} \int_{t_1}^{t_1 + T} x(t) dt = 0$

Form.asc

Version 4
SHEET 1 880 680
WIRE 288 32 112 32
WIRE 112 64 112 32
WIRE 112 176 112 144
WIRE 112 288 112 256
FLAG 112 288 0
FLAG 288 32 Uout
SYMBOL voltage 112 160 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(0 1 1k)
SYMBOL voltage 112 48 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value 3
TEXT 280 288 Left 2 !.tran 4m

Kenngrößen

$Schwingungsgehalt = \frac{Effektivwert des Wechselanteils} {Effektivwert der Mischgröße}$

$Effektive Welligkeit = \frac{Effektivwert des Wechselanteils} {Gleichwert der Mischgröße}$

$Riffelfaktor = \frac{Scheitelwert des Wechselanteils} {Gleichwert der Mischgröße}$

$Formfaktor = \frac{Effektivwert}{Gleichrichtwert}$

Effektivwert der Mischgröße: Wurzel der Summe der Quadrate der Effektivwerte

$u_{eff} = \sqrt{u_{eff1}^2 + u_{eff2}^2 + .. u_{effn}^2}$

Abschnittsweise Geradengleichung

Geradengleichung:

y = a x + b

Geradengleichung mit 2 Punkten:

$y = \frac{y_2 - y_1}{x_2 - x_{1}}\left(x - x_1 \right) + y_1$

2 Punkte: (x1,y1), (x2, y2)

(x1,y1) = (4,5), (x2, y2) = (8, 13)
Steigung:

$\frac{dy}{dx} = \frac{y2-y1}{x2-x1} = 2$
Gleichung:

$y = y1 + \frac{dy}{dx} \left( x - x1 \right)$

$y = 5 + 2 \cdot \left( x - 4 \right)$

Verifikation:
x = x1 :

$y(x1) = y1 + \frac{dy}{dx} \left( x1 - x1 \right) = y1$
x = x2 :

$y(x2) = y1 + \frac{dy}{dx} \left( x2 - x1 \right) = y1 + y2 - y1 = y2$

Integralrechnung (1)

Schritte

Ausmultiplizieren um Potenzen der Integralvariablen zu haben
$\int \left( 2 + 4x \right)^2 dx = \int 4 + 16 x + 16 x^2 dx$
In Summanden zerlegen (Regeln anwenden, um Listen anwenden zu können):
$\int 4 + 16 x + 16 x^2 dx = \int 4 dx + \int 16 x dx + \int 16 x^2 dx$
Stammfunktionen mit der Liste bilden
$\int 4 dx + \int 16 x dx + \int 16 x^2 dx = [ 4 x ] + [ 16 \frac{x^2}{2} ] + [ 16 \frac{x^3}{3} ]$
Obere Grenze - untere Grenze, Einsetzen
$[ 4 x ]_{x0}^{x1} + [ 16 \frac{x^2}{2} ]_{x0}^{x1} + [ 16 \frac{x^3}{3} ]_{x0}^{x1}$ $= 4 (x1 - x0) + 16 \frac{x1^2 - x0^2}{2} + 16 \frac{x1^3 - x0^3}{3}$

Integralrechnung (2)

Schritte

Listen:

$\int cos(ax) dx = \frac{1}{a} sin(ax)$

$\int sin(ax) dx = - \frac{1}{a} cos(ax)$

$\int cos^2 (ax) dx = \frac{x}{2} + \frac{1}{4a} sin(2 a x)$

$\int sin^2 (ax) dx = \frac{x}{2} - \frac{1}{4a} sin(2 a x)$

$\int a + b x + c x^2 dx = a x + b \frac{x^2}{2} + c \frac{x^3}{3}$

Regeln:

$\int a \cdot x dx = a \int x dx$

$\int_{x0}^{x1} f(x) dx = \left[ F(x) \right] = F(x1) - F(x0)$

$\int_{x0}^{x2} f(x) dx = \int_{x0}^{x1} f(x) dx + \int_{x1}^{x2} f(x) dx$

Numerische Integration

Es wird über eine Periode T integriert.
Die Periode T wird in n Abschnitte

$\frac{T}{n}$ geteilt.

Nach der Regel:

$\int\limits_{x0}^{x2} f(x) dx = \int\limits_{x0}^{x1} f(x) dx + \int\limits_{x1}^{x2} f(x) dx$
mit der Annahme die Funktion sei in einem sehr kleinen Abschnitt

$\frac{T}{n}$ näherungsweise konstant, ergibt sich:

$\int_{x0}^{x2} f(x) dx = \frac{T}{n} \sum\limits_{i=1}^{n} y_i$
Dies Verfahren wird bei Oszilloskopen angewendet. Man kann es auch mit Excel oder einer Programmiersprache (JavaScript) durchführen.

Numerische Lösung zur Ergebnisverifikation

	A	B	C	D
1	x	y	Integral	quadratisches Integral
2	0	4	4 * ( 1 - 0 )	4 * 4 *( 1 - 0 )
3	1	4	4 * ( 2 - 1 )	4 * 4 *( 2 - 1 )
.	.	.	y * ( x_n+1 - x_n )	y * y * ( x_n+1 - x_n )
.	.	.	y * ( x_n+1 - x_n )	y * y * ( x_n+1 - x_n )
42	40	-2

Gleichwert: 0.55

  =SUMME(C:C)/40

Effektivwert: 2.31

  =WURZEL(SUMME(D:D)/40)

Excel Funktion für Spalte B (y):
4 Abschnitte mit der WENN Funktion.

  =WENN(REST(A2;40)<10;4;
      WENN(REST(A2;40)<20;2-4/10*(REST(A2;40)-10);
	     WENN(REST(A2;40)<30;-2;0)))

Die numerische Genauigkeit ist abhängig von der Schrittweite.

Wiederholung (24.03.2025)

Beschreiben Sie die dargestellte Größe.

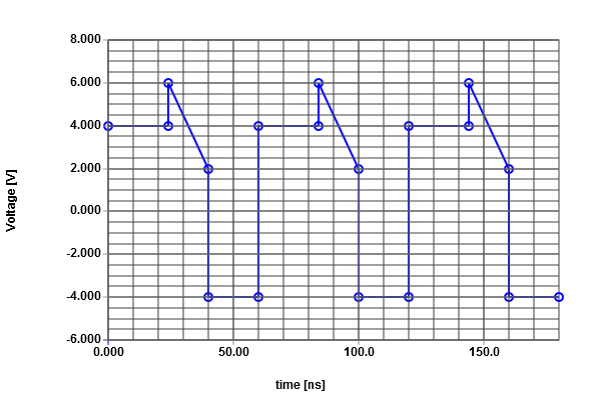
5n,3,5,4,0,3,6,-1.33,4,-4,0

Electronic Explorer by Digilent von Trenz

2016
Digilent Electronics Explorer Board - academic
(360.-EUR inkl. MWSt)
Oszilloskop: 4 channels
Spannungsmesser
Spannungsversorgung
Arbritary function generator: 2 channels
32 Digitale IO

2022
Digilent is part of National Instruments
Analog Discovery Studio
(665.- EUR inkl. MWSt.)
Oszilloskop: 2 channels
2025
Analog Discovery 3 (450.-)

Elektrisches Allzwecklabor ADALM2000

2022
Analog Devices
ADALM2000
(355.- EUR inkl. MWSt.)
Oszilloskop 2: channels
Arbitrary function generator: 2 channels
Power supply 0..5V. -5V..0V

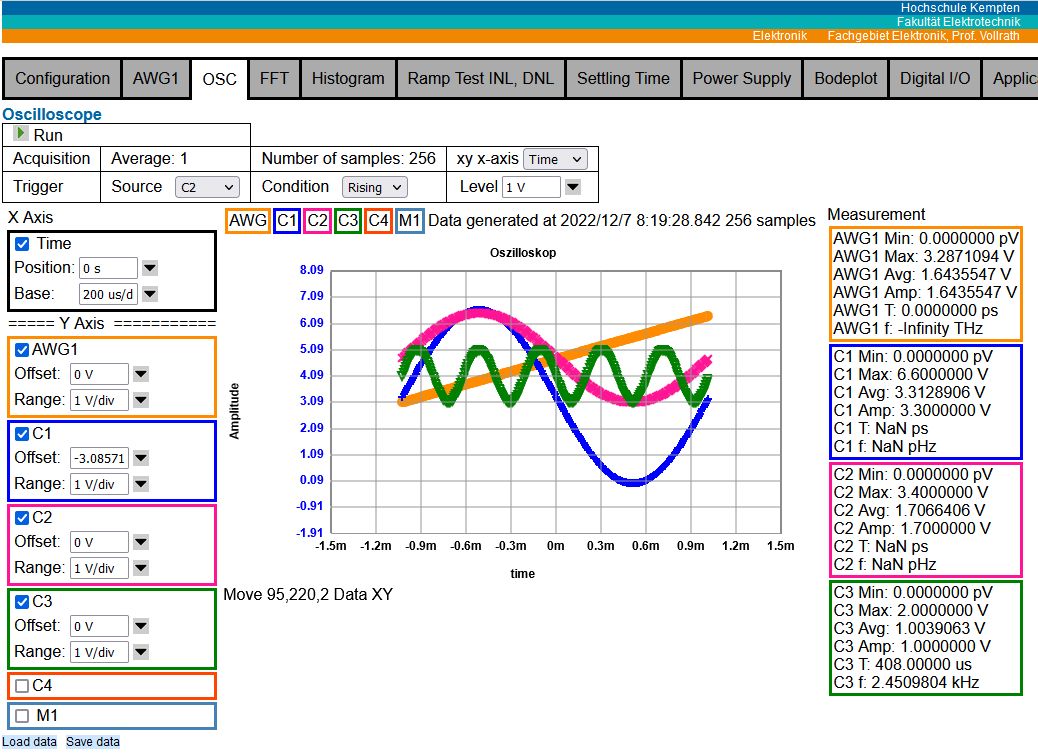
Elektrisches Allzwecklabor EEBench

2023
Forschungssemester
BASYS2, FPGA, VHDL
(150.- EUR inkl. MWSt.)
Oszilloskop 4 channels, 125 kSps
Arbitrary function generator: 1 channel 16 Bit R2R DAC
NodeJS, JavaScript Web interface

EEBench
Node EEBench

Github NodeEEBench

Arduino, RaspberryPi, JavaScript, Node.js, VHDL, HTML

Wirkleistung

Leistung P Augenblickswert
P(t) = u(t) · i(t)
Wenn u und i periodisch sind, ist auch P periodisch
Energie W
Integral der Leistung über die Zeit
$W = \int_{t1}^{t1+T} P(t) dt$
Wirkleistung (mittlere Leistung)
$P = \frac{1}{T} \int_{t1}^{t1+T} P(t) dt$

Motivation Effektivwert

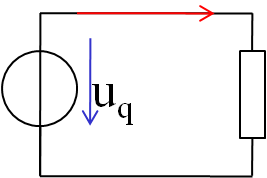
Vergleich der mittleren Leistung von Wechselstrom und Gleichstrom.

Wechselstrom	Gleichstrom

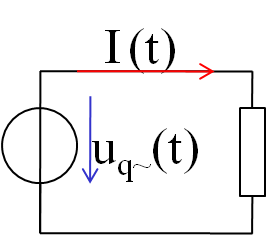
$P = \frac{1}{T} \int_{t_1}^{t_1 + T} u(t) \cdot i(t) dt$ $P = \frac{1}{T} \int_{t_1}^{t_1 + T} \frac{u^2(t)}{R} dt$	$P = U \cdot I$ $P = \frac{U^2}{R}$

Wenn die Leistungen gleich sein sollen ergibt sich:

$P = \frac{1}{T} \int_{t_1}^{t_1 + T} \frac{u^2(t)}{R} dt = \frac{U^2}{R}$
und umgeformt nach der entsprechenden Gleichspannung U:

$U = \sqrt{ \frac{1}{T} \int_{t_1}^{t_1 + T} u^2(t) dt }$

Test 03 Geradengleichung und Integral

Name:

Startzeit:

Geben Sie für den nebenstehenden Graphen die Geradengleichung an.

Integrieren Sie folgenden Term von 2 s bis 4 s.

u(t) = 3 V + 0.02 V/ms t + 3 V s^-2 t²

Test 04 C, Gleichwert, Effektivwert

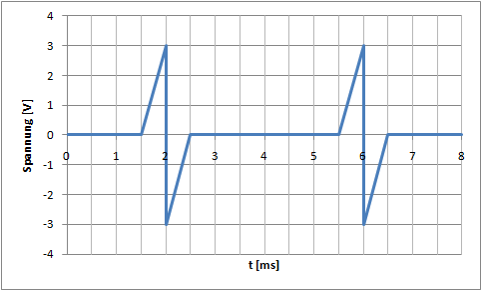
Gleichwert

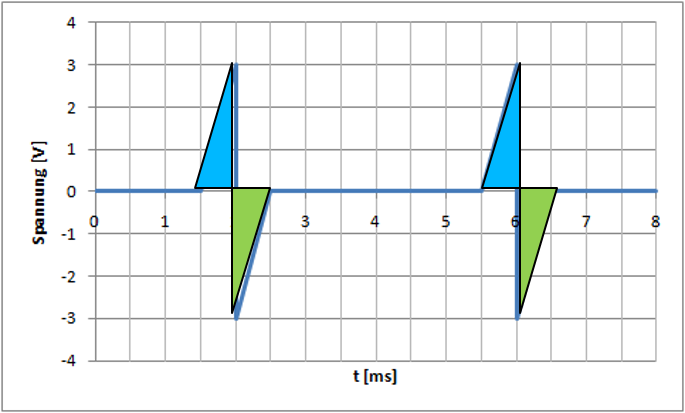
Gleichwert:

Anschaulich, Numerisch
Flächen zwischen Kurve und Nullachse
Oberhalb der Nullachse: positiv
Unterhalb der Nullachse: negativ

$\overline{u} = 0$

$\overline{u} = \frac{1}{T} \int_{0}^{T} u(t) dt$

$\overline{u} = \frac{1}{T} \left( \int_{5.5ms}^{6ms} \frac{3 V}{0.5ms}(t-5.5ms) dt + \int_{6ms}^{6.5ms}-3V + \frac{3V}{0.5ms} (t-6ms)dt \right)$

Gleichwert

$\overline{u} = \frac{1}{T} \left( \int_{5.5ms}^{6ms} \frac{3 V}{0.5ms}(t-5.5ms) dt + \int_{6ms}^{6.5ms}-3V + \frac{3V}{0.5ms} (t-6ms)dt \right)$

Integralgrenzen verschieben

$\overline{u} = \frac{1}{T} \left( \int_{0ms}^{0.5ms} \frac{3 V}{0.5ms}t dt + \int_{-0.5ms}^{0ms} \frac{3V}{0.5ms}tdt \right)$

Ausklammern und Stammfunktion bilden:

$\overline{u} = \frac{3 V}{2 ms^{2}} \left( \left[\frac{t^2}{2} \right]_{0ms}^{0.5ms} + \left[\frac{t^2}{2} \right]_{-0.5ms}^{0ms} \right)$

$\overline{u} = \frac{3 V}{2 ms^{2}} \left( \frac{(0.5ms)^2}{2} - \frac{(-0.5ms)^2}{2} \right) = 0$

Effektivwert

$U = \sqrt{\frac{1}{T} \int_{0}^{T} (u(t))^2 dt}$

Numerisch Excel

Analytisch
Start mit den verschobenen Grenzen
T = 4 ms

$U = \sqrt{\frac{1}{T} \left( \int_{0ms}^{0.5ms} \left( \frac{3 V}{0.5ms} t \right)^2 dt + \int_{-0.5ms}^{0ms} \left(\frac{3V}{0.5ms} t \right)^2 dt \right) }$

Effektivwert

Ausklammern und Stammfunktion bilden:

$U = \sqrt{ \frac{9 V^2}{1 ms^{3}} \left( \left[\frac{t^3}{3} \right]_{0ms}^{0.5ms} + \left[\frac{t^3}{3} \right]_{-0.5ms}^{0ms} \right) }$

$U = \frac{3 V}{ms} \sqrt{ \frac{1}{ms} \left( \frac{(0.5ms)^3}{3} - \frac{(-0.5ms)^3}{3} \right) } = \frac{1}{2} \sqrt{3} V = 0.866 V$

Nachdenken über die Lösung

Verifikation: Nachbar, Webanwendung, Simulation

Webanwendung: Unit, cycles, length1, start1, slope1, length2, start2, slope2, length3, start3, slope3
1m,2,1.5,0,0,0.5,0,6,0.5,-3,6,1.5,0,0

Graphische Interpretation
Numerische Interpretation: Abzählen von Flächenkästchen
Integral abschnittsweise über eine Periode bilden:
Konstante y=y0
Gerade y=y0+b(x-x0)
Verschieben entlang der x-Achse, um eine einfache Gleichung zu erhalten.
Integrieren
Formel hinschreiben
Einheiten: 1/(ms) ist keine Einheit Hz, kHz
Wie lange habe ich gebraucht?
Wie oft habe ich nachgeschaut?
Wie oft habe ich mich verrechnet?

Die programmierte Lösung zeigt, das es sich bei der Lösung um sehr einfache Operationen handelt, die nacheinander abgearbeitet werden.

Gleichrichtwert

Gleichrichterschaltung (rectifier circuit)
Der Strom fliesst nur in eine Richtung
Ideale Diode
UD > 0, R_D = 0 leitet
UD < 0, R_D = 8 sperrt
Einpuls Gleichrichterschaltung (half wave rectifier circuit)

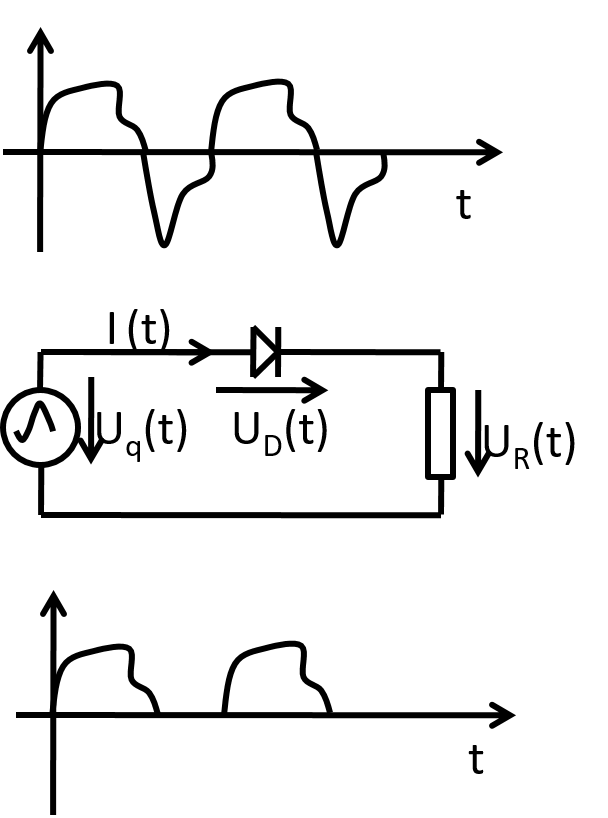
Gleichrichtwert

Gleichrichterschaltung (rectifier circuit)
Der Strom fliesst nur in eine Richtung
Brückengleichrichter (bridge rectifier circuit)

Gleichrichtwert

$|\overline{u}| = \frac{1}{T} \int_0^{T} |u(t)| dt$

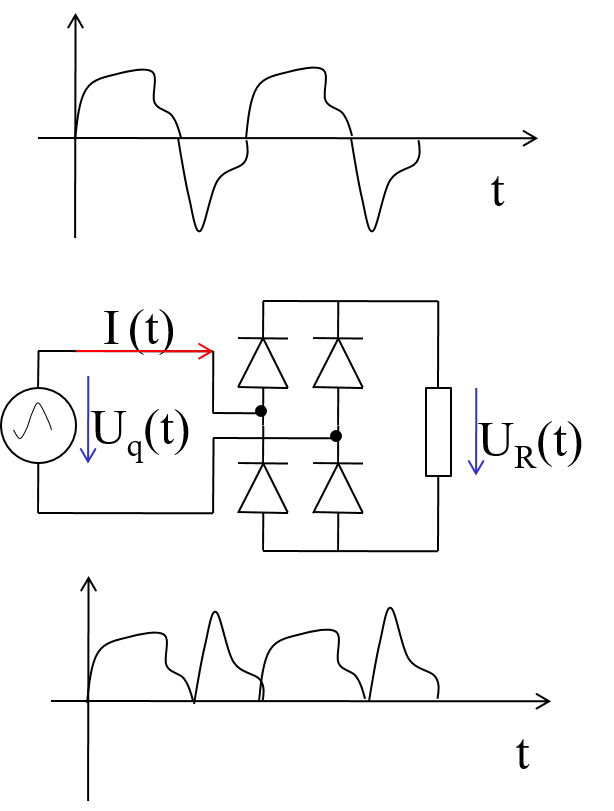
Effektivwert einer Mischgröße

Zeitfunktion

$u(t) = u_0 + \hat{u}_1 sin \omega t$

Effektivwert

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt }$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T (u_0 + \hat{u}_1 sin \omega t)^2 dt }$

$U_{eff} = \sqrt{\frac{1}{T} \int_0^T \left( u_0^2 + \hat{u}_1^2 sin^2 \omega t + 2 u_0 \hat{u}_1 sin \omega t \right) dt }$

Integral von 0 bis T von sinωt ist 0.

$U_{eff} = \sqrt{ \frac{1}{T} \left( \int_0^T u_0^2 dt + \int_0^T \hat{u}_1^2 sin^2 \omega t dt \right) }$

$U_{eff} = \sqrt{ U_{0eff}^2 + U_{1eff}^2 }$

Beispiele Wechselgrößen

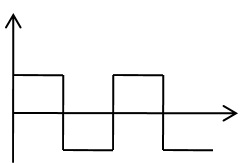	Rechteck
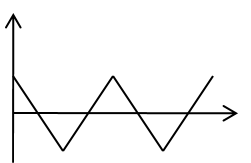	Dreieck
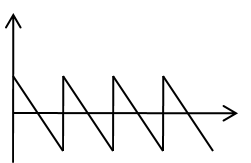	Sägezahn
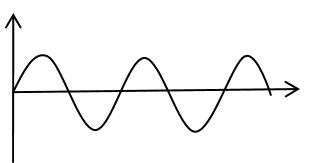	Sinus

Periode, Frequenz, Gleichrichtwert, Effektivwert
Offset, Gleichwert
Phasenverschiebung
Effektivwert, Formfaktor, Wikipedia

Zusammenfassung

Mittelwerte: Gleichwert, Effektivwert
Beispiel: Rechnung, numerische Integration, Simulation
Gleichrichtwert
Tabellen, Wechselgrößen

Test Geradengleichung und Integral (2024)

Aufgabe	Richtig	Gesamt
Geradengleichung	14	17
Umrechnung 0.02 V/ms in V/s	12	17
Integralrechnung	8	17
Nicht Verrechnet	12	17

Nächstes Mal:
03 Sinusförmige Wechselgrößen

Fragen

Wer hat am Mathevorkurs teilgenommen? (11/21)
Wer hat am MINTENSIV teilgenommen? (3/21)
In welchem Format würden Sie ein Fachbuch kaufen?
EBook (6), Papier (17), Beides (2), Keines, Nur Skript (5)
Bei welchem Preis würden Sie ein Fachbuch kaufen?
Unsonst, 5.- (20/21), 10.- (21/21), 20.-(12/21), 50.-(2/21), 100.-
Würden Sie für sich selbst Hardware kaufen?
(Arduino, RaspberryPi, Oszilloskop (14/21 umsonst), Multimeter)?
Ja/Nein
Umsonst (17/21), 30.- (11/21),
Haben Sie ein Arduino board, RaspberryPi, ESP32, Multimeter, FPGA Board gekauft? (11/21)
Bis zu welchem Preis würden Sie ein Allzwecklabor kaufen?
Nur umsonst, 50.-, 100.-, 200.-, 400.-

2025 GET 2 02 Wechselgroesse Prof. Dr. Joerg Vollrath

Grundlagen Elektrotechnik 2 (GET2)

02 Wechselgrößen

Gleichwert, Effektivwert

Prof. Dr. Jörg Vollrath

Video der 19. Vorlesung 8.6.2021

Rückblick und Heute

Vorsatzzeichen, Periode, Frequenz

Diskutieren Sie mit ihrem Nachbarn:

Ziele

Mittelwerte periodischer Größen

Gleichwert (direct component, DC)

Mittelwerte periodischer Größen

Effektivwert (root mean square value)

Integralrechnung

Beispiel Mischgröße

Abschnittsweise

Geradengleichung

Integralbildung

Beispiel Mischgröße

Abschnittsweise Geradengleichung

Integralbildung mit verschobenen Grenzen

Ergebnis Test 1 und 2 (19.03.2025)

Strom- und Spannungsformen

Kenngrößen

Abschnittsweise Geradengleichung

Integralrechnung (1)

Schritte

Integralrechnung (2)

Schritte

Listen:

Regeln:

Numerische Integration

Numerische Lösung zur Ergebnisverifikation

Wiederholung (24.03.2025)

Electronic Explorer by Digilent von Trenz

Elektrisches Allzwecklabor ADALM2000

Elektrisches Allzwecklabor EEBench

Wirkleistung

Motivation Effektivwert

Test 03 Geradengleichung und Integral

Test 04 C, Gleichwert, Effektivwert

Gleichwert

Gleichwert:

Gleichwert

Effektivwert

Effektivwert

Nachdenken über die Lösung

Gleichrichtwert

Gleichrichtwert

Gleichrichtwert

Effektivwert einer Mischgröße

Beispiele Wechselgrößen

Zusammenfassung

Test Geradengleichung und Integral (2024)

Fragen