Grundlagen Elektrotechnik 2 (GET2)05 ZeigerdarstellungKomplexe RechnungProf. Dr. Jörg Vollrath04 SPICE |

|
Video GET2 05 Zeigerdarstellung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht (31.03.2025)
- Wer hat SPICE runtergeladen?
- Wer hat eine SPICE Simulation durchgeführt?
- Zeigerdarstellung
- Überlagerung von Sinusgrößen
Ziele
- Sie können eine sinusförmige Wechselgröße als Zeiger und komplexe Zahl darstellen.
- Sie können Zeiger graphisch Addieren.
- Sie können mit komplexen Zahlen rechnen und kennen die P-Form und die R-Form.
Zeigerdarstellung

|
Addition im Zeigerdiagramm
- Normierung
Eine Spannung(Strom) wird mit einem Skalierungsfaktor in eine Länge(cm) umgerechnet, damit alle Größen bei der Zeichnung auf ein Blatt passen. - Der erste Zeiger wird angetragen.
- Bei einer Addition wird der Anfang(Fuß) des nächsten Zeigers an das Ende(Spitze) des ersten Zeigers angesetzt.
- Bei einer Subtraktion wird die Richtung des Zeiger der subtrahiert wird umgedreht.
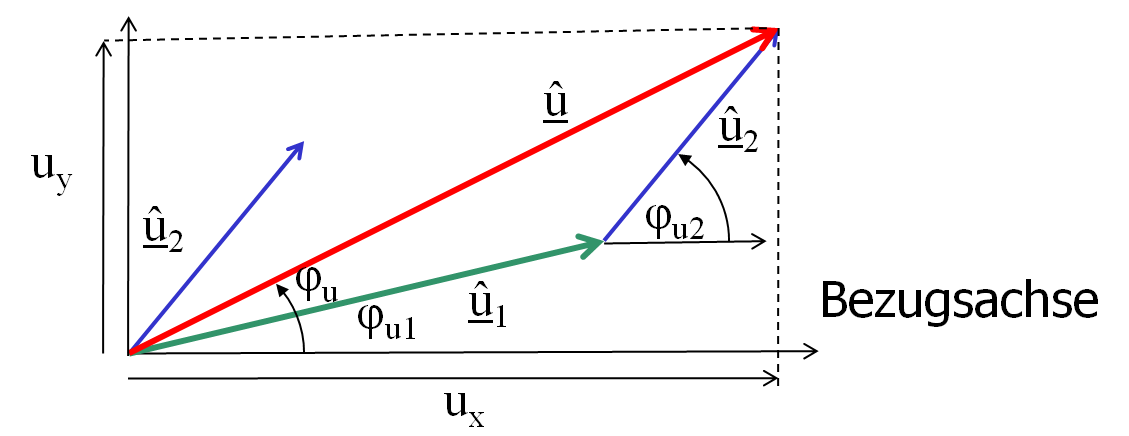
Beispiel: Überlagerung von Sinusgrößen gleicher Frequenz
Zwei Quellen mit sinusförmiger Quellenspannung gleicher Frequenz sind in Reihe geschaltet.
\( \hat{u}_{q1} = 50 V; \phi_{u1} = 80°; f_1 = 50 Hz; \) \( \phi = \frac{80°}{180°} \cdot \pi = 1.3298 \)
\( \hat{u}_{q2} = 30 V; \phi_{u2} = 15°; f_2 = 50Hz; \)
Komplexe Symbole
|
|
R-Form und P-Form
R-Form |
P-Form |
|
\( \underline{Z} = R + j X \) \( R = Z cos\phi \) \( X = Z sin\phi \) Addition von Spannungen und Strömen Reihenschaltung von Widerständen \( \underline{Z} = R + j X = \underline{Z}_1 + \underline{Z}_2 \) \( \underline{Z} = (R_1 + R_2) + j (X_1 + X_2) \) |
\( \underline{Z} = Z \underline{/\phi} = Z \cdot e^{j\phi}\) \( Z = \sqrt{R^{2} + X^{2}} \) \( \phi = arctan{\frac{X}{R}} \) Multiplikation, Division Umwandlung Widerstand und Leitwert |
Rechnung für Sinusförmige Wechselgrößen
Überlagerung sinusförmiger Wechselgrößen
|
Komplexe Symbole P-Form: Polarkoordinaten
- \( \underline{u}(t)=\hat{u} e^{j(\omega t + \phi_u)} \)
- Vollständiges komplexes Symbol
- Realteilbildung
u(t) = Re{u(t)} = û cos (ω t + φu) - Verzichtet auf die Darstellung der Zeitabhängigkeit
Symbol für die Zeit t=0 - Versorzeichen /
- û
= û /φu
= û ej φu
- U
= U /φu
= U ej φu Effektivwert
- Sprich U Versor φu
- Der Winkel erscheint in normaler Schrifthöhe und Größe
- Darstellung in Polarkoordinaten P-Form
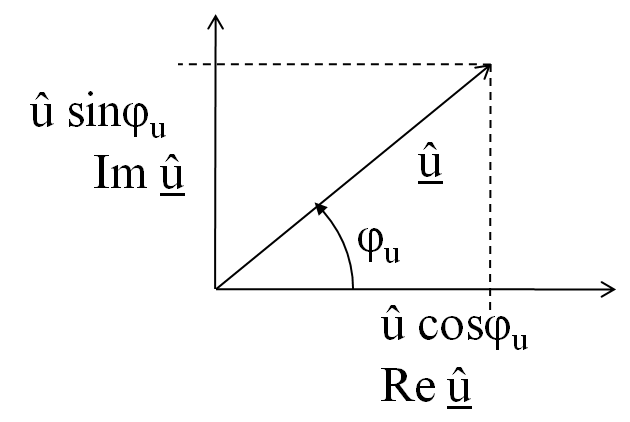
Komplexe Symbole R-Form: rechtwinklige Koordinaten
- R-Form
U = U cos φu + j U sin φu
- Beispiel: Addition zweier Spannungen
- Uq1 = 17.68 V /75°
- Uq2 = 10.6 V /12°
- Uq1 = 17.68 V /75° = 4.58 V + j 17.08 V
- Uq2 = 10.6 V /12° = 10.37 V + j 2.2 V
- Addition Realteile und Imaginärteile
- Uq1 + Uq2 = 14.95 V + j 19.28 V
- P-Form
- \( \underline{U} = \sqrt{Re\{\underline{U}\}^2 + Im\{\underline{U}\}^2} \underline{/ arctan \left( \frac{Im\{\underline{U}\}} {Re\{\underline{U}\}}\right)} \)
- U = 24.4 V /52.2°
Formelzeichen für Wechselgrößen
- u zeitlich veränderliche elektrische Spannung
- û Amplitude, Maximalwert der sinusförmigen Spannung
- u komplexe Zeitfunktion der elektrischen Spannung
- û komplexe Amplitude der elektrischen Spannung
- U elektrische Spannung (Gleichspannung, Effektivwert)
- U komplexer Effektivwert der elektrischen Spannung
- Unterstreichen: komplex
- û Amplitude
Fragen
- Beschreiben Sie die Konstruktion des Liniendiagramms einer Sinusschwingung mit Hilfe eines rotierenden Zeigers.
- Wie lautet das vollständige komplexe Stromsymbol?
- Worin besteht der Unterschied zwischen dem vollständigen komplexen Symbol einer Spannung und der komplexen Spannung?
- Welche Kenngrößen einer Sinusschwingung werden im komplexen Symbol verwendet?
- Unter welcher Voraussetzung kann die Addition von Sinusschwingungen auf die Addition der komplexen Symbole zurückgeführt werden?
Rechnung für Sinusförmige Wechselgrößen
- Überlagerung sinusförmiger Wechselgrößen
- Differentialgleichungen
- Im Zeitbereich
- Mit Hilfe von komplexen Zeitfunktionen
- Berechnung im komplexen
- Zeigerdiagramm mit komplexen Effektivwerten (grafisches Verfahren)
- Algebraische Gleichung in komplexen Effektivwerten (Symbolische Methode)
Test Reihenschaltung komplexer Spannungsquellen
Zwei sinusförmige Spannungsquellen Uq1 = 10 V /30° und Uq2 = 20 V /60° sind in Reihe geschaltet.
Bestimmen Sie die Gesamtspannung rechnerisch und mit einem Zeigerdiagramm.
Komplexe Zahlen und Operationen
| z = x + j y | mit \( j = \sqrt{ -1} \) |
| z = r ( cos φ + j sin φ) | mit \( r = |z| = \sqrt{x^2 + y^2} \) mit φ = arctan(x/y) |
| z = r ejφ | Eulersche Formel |
Operationen
Multiplikation, Division, Differential\( \underline{z}_1 \underline{z}_2 = r_1 r_2 e^{j(\phi_1 + \phi_2)} = r_1 r_2 \underline{/ \phi_1 + \phi_2} \)
\( \frac{\underline{z}_1}{ \underline{z}_2} = \frac{r_1}{ r_2} e^{j(\phi_1 - \phi_2)} = \frac{r_1}{ r_2} \underline{/\phi_1 - \phi_2} \)
\( \frac{d e^{j \omega t}}{dt} = j \omega e^{j \omega t} \)
Fragen
- Was sind die Vorteile der Berechnung von Spannungen und Strömen im komplexen?
- Was sind die R-Form und die P-Form?
- Wie führen Sie die R-Form in die P-Form über?
- Wann wenden Sie die R-Form an, wann die P-Form?
- Welche praktische Bedeutung hat die Überlagerung von sinusförmigen Wechselgrößen?
- Was passiert bei der Überlagerung von sinusförmigen Wechselgrößen gleicher Frequenz?
- Was passiert bei der Überlagerung von sinusförmigen Wechselgrößen unterschiedlicher Frequenz?
Zusammenfassung und nächstes Mal
- Zeigerdarstellung
- Addition von Zeigern
- Komplexe Symbole
- P-Form: Versorschreibweise
- R-Form
- Umrechnung zwischen P-Form und R-Form
Reihenschaltung R und L: Berechnungsbeispiel

- Differentialgleichungen
- u(t) = û sin(ωt+φu) = R i(t) + L di/dt
- Strom: i(t) =
î ejωt
d i(t)/dt = jω î ejωt
- Im komplexen
- u(t) = û ej(ωt+φu) = R i(t) + j ω L i(t)
- Algebraische Gleichung: Effektivwerte
- U = (R + j ω L )I
- Zeigerdiagramm
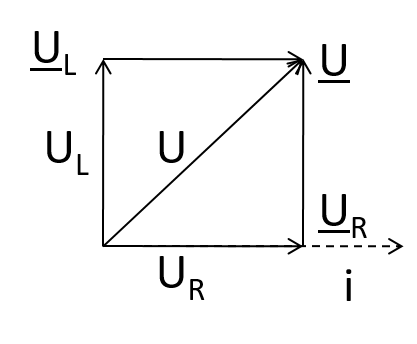
|
\( \underline{U} = j \omega L \underline{I} \) |
|
\( u_L = L \frac{di}{dt} \) |
Hilfsmittel Differentialgleichung
|
\( u_L = L \frac{di}{dt} \) |
\( \frac{d sin(\omega t + \phi)}{dt} = \omega cos(\omega t+\phi) \)
i = î sin(ωt + φ)
uR = R i = R î sin(ωt + φ)
uL = L di/dt = ω L î cos(ωt + φ)
u = uR + uL = R î sin(ωt + φ) + ω L î cos(ωt + φ)
u = uR + uL = R î sin(ωt + φ) + ω L î sim(ωt + φ + π/2)
Die Überlagerung zweier Sinusschwingungen ergibt wieder eine Sinusgröße