Grundlagen Elektrotechnik 2 (GET2) 06 Komplexe lineare Zweipole Prof. Dr. Jörg Vollrath 05 Zeigerdarstellung

Übersicht

• Zeigerdarstellung
• Addition von Zeigern
• Komplexe Symbole
• P-Form: Versorschreibweise
• R-Form
• Umrechnung zwischen P-Form und R-Form
• Lineare passive Zweipole
• Komplexer Widerstand und Leitwert
• Lineare aktive Zweipole
• Ideale und lineare Sinusquelle
• Leistung
• Scheinleistung, Wirkleistung, Komplexe Leistung
• Grundzweipole
• Idealer Ohmscher, induktiver, kapazitiver Zweipol

Rückblick, Heute

• Komplexe Spannung
• u(t) = û cos(ωt + φ_u)        U = U /φ_u (Effektivwert)
• Komplexe Rechnung
• R-Form: x = a + j b      a = x cos φ      b = x sin φ
• P-Form: x = x e^{j φ}      \( x = \sqrt{a^2 + b^2} \)      φ = arctan(b/a)

Wie wenden wir die komplexe Rechnung an?

• Was bedeutet das für passive Bauteile (Widerstände)? R,L,C
• Z = R + j X      Y = G + j B
• Y = 1 / Z      konjugiert komplex erweitern.
• Was bedeutet das für lineare Quellen (aktive Zweipole)?
• Quellenumwandlung
• Wie berechnen wir die Leistung?

Inhalt

• Lineare passive Zweipole
• Komplexer Widerstand und Leitwert
• Lineare aktive Zweipole
• Ideale und lineare Sinusquelle
• Leistung
• Scheinleistung
• Wirkleistung
• Komplexe Leistung
• Grundzweipole
• Idealer Ohmscher Zweipol
• Idealer induktiver Zweipol
• Idealer kapazitiver Zweipol

Komplexer Widerstand und Leitwert

• Sinusspannung Φ_U, Sinusstrom Φ_I
• Phasenverschiebung
• Komplexer Widerstand
  \( \underline{Z} = \frac{\underline{U}}{\underline{I}} = R + jX = Z e^{j\phi} \)
• Frequenzabhängig
  \( \underline{Z} = \frac{U e^{j(\omega t + \phi_{U})}}{I e^{j(\omega t + \phi_{I})}} = \frac{U e^{j \phi_{U}}}{I e^{j\phi_{I}}} = \frac{U}{I} e^{j(\phi_{U} - \phi_{I})} \)
• komplexer Koeffizient, Operator
• Versorschreibweise
  \( \underline{Z} = \frac{U}{I} \underline{/\phi_U - \phi_I} \)

Komplexer Widerstand und Leitwert

• Betrag des komplexen Widerstands
• Scheinwiderstand oder Impedanz
  \( Z = \frac{U}{I} \) [Z] = 1 Ω
• Winkel φ_Z Phasenverschiebungswinkel, Phasenwinkel
• φ_Z = φ_U - φ_I = φ

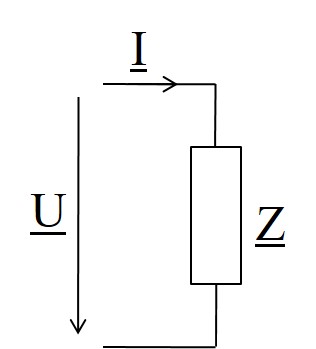
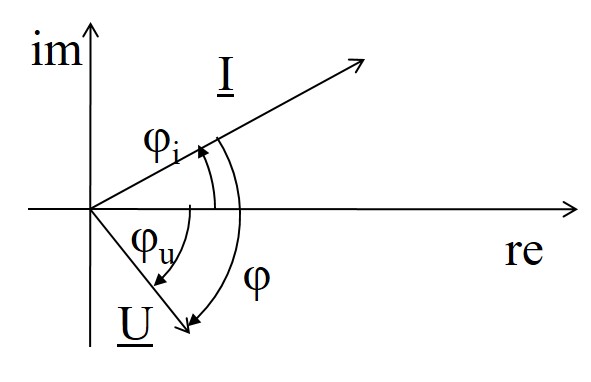
Gleichung des komplexen Widerstands und Leitwerts

• P-Form und R-Form
  \( \underline{Z} = Z \underline{/\phi} = R + j X \)
• Realteil R: Wirkwiderstand, Resistanz (resistance)
• Imaginärteil X: Blindwiderstand, Reaktanz (reactance)
• Komplexer Leitwert \( \underline{Y} \):
  \( \underline{Y} = \frac{\underline{I}}{\underline{U}} = \frac{1}{\underline{Z}} \)
• Betrag des komplexen Leitwerts:
• Scheinleitwert, Admittanz
  \( Y = \frac{I}{U} = \frac{1}{Z} \) [Y] = 1 S

Gleichung des komplexen Widerstands und Leitwerts

• Winkel φ_Y negativer Phasenverschiebungswinkel
• P-Form und R-Form
  \( \underline{Y} = Y \underline{/-\phi} = G + j B \)
• Realteil G: Wirkleitwert, Konduktanz (conductance)
• Imaginärteil B: Blindleitwert, Suszeptanz (susceptance)
• \( \underline{Y} \) komplexer Operator, bei konstanter Frequenz ein konstanter Wert

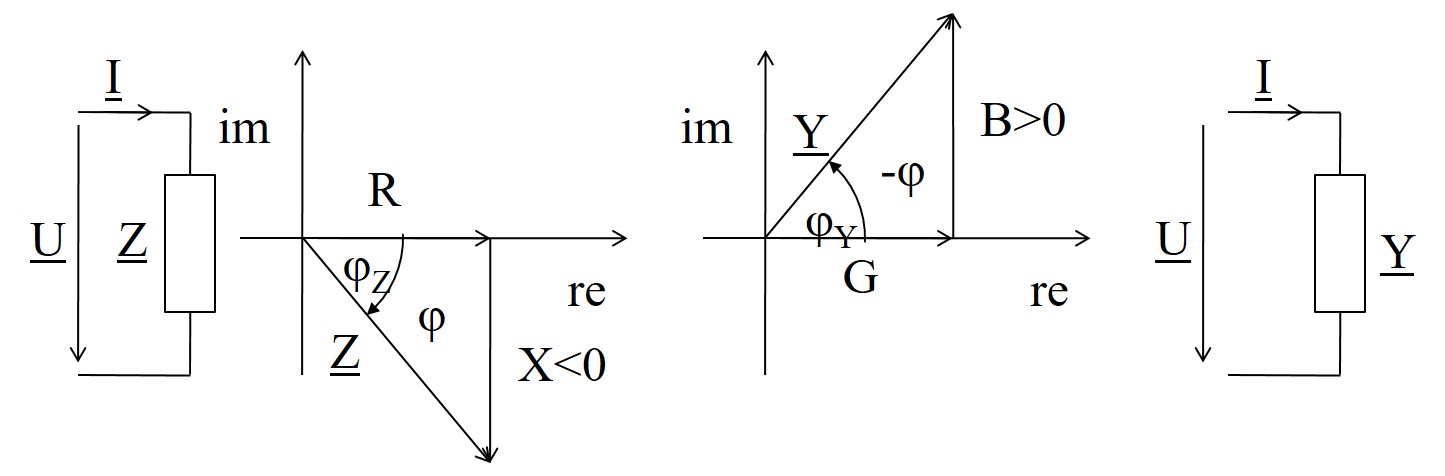
R-Form und P-Form (05.04.2023)

R-Form	P-Form
\( \underline{Z} = R + j X \) \( R = Z cos\phi \) \( X = Z sin\phi \) Addition von Spannungen und Strömen Reihenschaltung von Widerständen \( \underline{Z} = R + j X = \underline{Z}_1 + \underline{Z}_2 \) \( \underline{Z} = (R_1 + R_2) + j (X_1 + X_2) \)	\( \underline{Z} = Z \underline{/\phi} = Z \cdot e^{j\phi}\) \( Z = \sqrt{R^{2} + X^{2}} \) \( \phi = arctan{\frac{X}{R}} \) Multiplikation, Division Umwandlung Widerstand und Leitwert

Überführung Z, Y

\( \underline{Z} = R + j X \)

Konjugiert komplex Erweitern:
\( \underline{Y} = \frac{1}{\underline{Z}} = \frac{1}{R+jX} = \frac{1}{R+jX} \frac{R - jX}{R - jX} =\frac{R - jX}{R^2 + X^2} \)

\( \underline{Y} = \frac{R}{R^2 + X^2} - \frac{jX}{R^2 + X^2} \)

\( \underline{Y} = \frac{1}{\underline{Z}} = \frac{1}{Z e^{j\phi_Z}} = \frac{1}{Z} e^{-j\phi_Z} \)

Beispiel

An einem linearen Zweipol liegt eine Sinusspannung mit dem Effektivwert U = 100V. Dabei fliesst ein Strom I = 2.5 A der der Spannung um 30° voreilt.

Berechnen Sie den komplexen Widerstand und den komplexen Leitwert.

Test

An einem linearen Zweipol liegt eine Sinusspannung mit dem Effektivwert U = 50V. Dabei fliesst ein Strom I = 0.4 A der der Spannung um 45° voreilt.

Berechnen Sie den komplexen Widerstand und den komplexen Leitwert in P- und R-Form.

Fragen

• Welche Eigenschaften hat ein linearer Zweipol?
• Was ist ein passiver Zweipol?
• Wie sind der komplexe Widerstand und der komplexe Leitwert definiert?
• Was versteht man unter dem Scheinwiderstand?
• Geben Sie den komplexen Widerstand und den komplexen Leitwert in der R-Form an und benennen Sie die Komponenten.
• Welcher Zusammenhang besteht zwischen dem Phasenverschiebungswinkel der Spannung gegen den Strom und dem Winkel des komplexen Widerstandes bzw. des komplexen Leitwerts?
• Wie rechnet man den komplexen Leitwert in den komplexen Widerstand um?

Zusammenfassung und nächstes Mal

• Komplexer Widerstand und Leitform
• P-Form, R-Form und Umrechnung

Ersatzquellen