Übungen Grundlagen Elektrotechnik 2

Übung 1: Wechselgrößen

Aufgabe 1: Rechteck Wechselgröße

Gegeben sei folgendes Oszillogramm einer Wechselgröße. 1.1 Lesen Sie die Charakteristischen Größen ab. 1.2 Berechnen Sie den Effektivwert, den Gleichwert und den Gleichrichtwert durch Integration und durch numerische Integration. Nach welcher Zeit wiederholt sich die Signalform? Periodendauer: T = 3 us Frequenz: f = 1/T = 333 kHz Vpp = 4 V v = 2 V Gleichwert: \( v_{gl} = \frac{1}{T} \int_{0}^{3us} v(t) dt \) Die Funktion ist abschnittsweise definiert: \( v_{gl} = \frac{1}{T} \left( \int_{0}^{2us} -1.5 V dt + \int_{2us}^{2.5us} 2.5 V dt + \int_{2.5us}^{3us} 1 V dt \right) \) Die Stammfunktion von y(t) = a ist Y = a t \( v_{gl} = \frac{1}{T} \left( [-1.5 V t]_{0}^{2us} + [2.5 V t]_{2us}^{2.5us} + [1 V t]_{2.5us}^{3us} \right) \) Man setzt die Grenzen ein: \( v_{gl} = \frac{1}{3 us} \left( -1.5 V 2 us - ( -1.5 V 0 us ) + 2.5 V 2.5 us - 2.5 V 2 us + 1 V 3 us - 1 V 2.5us \right) \) v_gl = ( -3 V us + 1.25 V us + 0.5 V us ) / (3 us) = - 5/12 V = - 0.417 V Mit der Internetseite Wechselgrößen und der Definition: 0.5u,3,4,-1.5,0,1,2.5,0,1,1,0 Für den Gleichrichtwert kann man die Definition ändern: 0.5u,3,4,1.5,0,1,2.5,0,1,1,0 Man kann die Werte mit LTSPICE verifizieren. Man definiert eine Spannungsquelle. V1 U1 0 PWL(0 -1.5 2us -1.5 2.001us 2.5 2.5us 2.5 2.501us 1 3u 1) Man schliesst einen Widerstand an. R1 U1 0 100k Man simuliert das Zeitverhalten für eine Periode: .tran 3us Man stellt U1 dar und bewegt die Maus über die Beschriftung U1 und drückt <STRG> rechte Maustaste. Average (Gleichwert): -417 mV RMS (Effektivwert): 1.645 V Aufgabe 2: 1m,3,4,4,1.5,2,10,-1.5,2,7,-1.5 Aufgabe 3: 1m,3,2,3,1,1,5,0,2,5,-1,1,3,0
Aufgabe 2: Wechselgröße 2.1 Wie bezeichnet man die dargestellte Größe? 2.2 Berechnen Sie die Phasenverschiebung der zwei Kurven. 2.3 Berechnen Sie die Kenngrößen der gezeigten Kurve.
Aufgabe 3 Wechselgrößen 3.1 Wie bezeichnet man diese Größe? 3.2 Berechnen Sie die Phasenverschiebung der zwei Kurven. 3.3 Berechnen Sie die Kenngrößen der gezeigten Kurve.
Aufgabe 4 SPICE Gegeben ist folgendes Schaltbild. Erstellen Sie die Netzliste. Die Spannungsquelle soll 5V Amplitude bei 100kHz haben. Wie lautet die Analyseanweisung um die ersten 2 Perioden der Spannungsquelle darzustellen?

Übung 2: Leistung, Grundzweipole, Zeigerdiagramm

Aufgabe 1

Zwei Quellen mit sinusförmiger Quellenspannung gleicher Frequenz sind in Reihe geschaltet.
\( \hat{u}_{q1} = 8 V; \phi_{u1} = 70 °; f_1 = 2 kHz \)
\( \hat{u}_{q2} = 6 V; \phi_{u2} = 20°; f_2 = 2 kHz \)
Zeichnen Sie die Liniendiagramme sämtlicher Spannungen und berechnen Sie die resultierende Spannung.
Geben Sie alle Spannungen in P-Form und R-Form an.

Aufgabe 2

Die Parallelschaltung aus einer idealen Stromquelle \( \underline{I}_q = 0.2 A \underline{/0°} \) und einem Zweipol \( \underline{Y}_i = 0.7 mS \underline{/60°} \) bilden eine lineare Stromquelle nach folgendem Bild.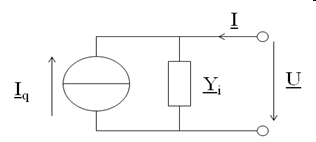

Berechnen Sie die Leerlaufspannung und den Kurzschlussstrom und die Daten für die äquivalente Ersatzspannungsquelle.

Aufgabe 3 Leistung

Ein Verbraucher bezieht von einem Generator bei der Klemmenspannung U = 9 V einen der Spannung um 30° vorauseilenden Strom von \( I = 0.6 A\).
Berechnen Sie die komplexe Leistung, die Scheinleistung, Wirkleistung und die Blindleistung. (Art)

Aufgabe 4 Leistung

Ein Verbraucher nimmt die Wirkleistung 140 kW auf. Die Blindleistung beträgt 70 kvar.
Welchen Wert hat sein Leistungsfaktor? Formulieren Sie eine komplexe Leistung.

Aufgabe 5 Komplexer Zweipol

Ein idealer Zweipol L = 15 mH liegt an der Sinusspannung U = 80 V; f= 500 Hz.
Wir wollen den komplexen Widerstand, den komplexen Leitwert sowie den Strom und die Blindleistung berechnen.

Aufgabe 6 Komplexer Zweipol, Leistung

An einem Grundzweipol fließt bei einer Spannung von 230 V ein Strom von 308 mA.
Berechnen Sie jeweils für einen Grundzweipol R, L und C den Wirk und den Blindwiderstand.
Berechnen Sie die dazugehörige Leistung.

Aufgabe 7

Eine Spannungsquelle \( U_q = 40 V \underline{/20°} \) (f = 2 kHz) mit einem Innenwiderstand \( \underline{Z}_i = 8 \Omega + j 15 \Omega \) wird extern mit einem Grundzweipol L = 6 mH beschaltet.
Berechnen Sie den Strom.
Stellen Sie die Ströme und Spannungen im Zeigerdiagramm dar.
Berechnen Sie den Gesamtwiderstand der Reihenschaltung.
Stellen Sie die Widerstände im Zeigerdiagramm dar.
Berechnen Sie die komplexe Leistung die am Innenwiderstand und am Grundzweipol L auftritt.

Aufgabe 8

An eine Stromquelle \( \underline{I}_q = 20 mA\underline{/30°} \) mit einem Innenleitwert \( \underline{Y}_i = 4 mS + j 6 mS \) ist ein Verbraucherwiderstand angeschlossen.
Es wird die Spannung \( U = 2 V \underline{/-20°} \) gemessen. Berechnen Sie den komplexen Verbraucherwiderstand!

Übung 3: Netze, Resonanz

Aufgabe 1

Berechnen Sie den komplexen Eingangsleitwert eines abgeglichenen
Tastkopfes nach folgendem Bild bei 1k Hz.
Geben Sie das Ersatzschaltbild an.
Berechnen Sie das Verhältnis der Spannungen \( \frac{U_E}{U_M} \) für:
\( R_T = 9M \Omega \), \( C_E = 10 pF, R_E = 1 M\Omega \).
Bestimmen Sie erst \( C_T \) im abgeglichenen Fall.

( \( \underline{Y} = 0.1 \mu S + j 6.28 nS \), U_E = 0.1 U_M, C_T = 1.1 pF )

Aufgabe 2

Von einer Kapazität sind die Elemente der Parallelschaltung bekannt: \( R_P = 1 M\Omega ; C_P = 22 nF \).
Berechnen Sie die Elemente der Reihen-Ersatzschaltung für \( f_1 = 100 Hz \) und für \( f_2 = 300 Hz\).
\( (R_s(f_1) = 5.23 \Omega; C_s(f_1) = 22 nF; R_s(f_2) = 0.582\Omega;C_s(f_2) = 22 nF) \)

Aufgabe 3 Komplexer Widerstand

Berechnen Sie für die folgende Schaltung den komplexen
Eingangswiderstand in R- und P-Form bei
einer Eingangsspannung von 8 V und f = 1 kHz.
\( R = 220 \Omega; C_P = 3.3 \mu F; R_S = 39 \Omega; L_S = 15 mH \).
Berechnen Sie die Resonanzfrequenz.
\( (f_r = 619 Hz, \underline{Z} = 234 \Omega - j 88 \Omega = 250 \Omega \underline{/ -21°}) \)
Verifikation mit LTSPICE:
Herunterladen von Uebung_03_03.asc (Rechtsclick und Speichern unter)
AC Simulation und Darstellung von V(u1)/I(R)
Mit Click auf y-Achsenbeschriftung lineare Darstellung wählen.
Ablesen des Winkels und des Betrags bei 1 kHz.

Aufgabe 4 Resonanz

Berechnen Sie den komplexen Widerstand folgender Schaltung.
\( R_1 = 10 k\Omega ; C_1 = 6.8 \mu F, R_2 = 10 \Omega; L_1 = 4mH \).
Es liegt eine Spannung von 8 V (200 Hz) an.
Berechnen Sie den Strom durch \( R_2 \).
Simulieren Sie die Schaltung in LTSPICE.

Berechnen Sie die Resonanzfrequenz.
Berechnen Sie die Spannungsüberhöhung bei Resonanz.
Simulieren Sie die Schaltung bei Resonanz in LTSPICE.
\( ( \underline{Z} = 11.8 \Omega -j 128 \Omega = 128.12 \Omega \underline{/-84.7°}; \)
\( \underline{I} = 156 mA\underline{/84.7°}; f = 1027 Hz; K_u = 2.56) \)

Übung 4:

Aufgabe 1: Komplexer Widerstand und Ortskurve Geben Sie die Netzfunktion des komplexen Widerstandes an. Bestimmen Sie den komplexen Widerstand für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. Zeichnen Sie die Ortskurve. Lösung
Aufgabe 2 An die Schaltung mit \( R_1 = 220 \Omega, C_2 = 680 nF, R_3 = 390 \Omega, C_3 = 82 nF \) werden die Sinusspannungen \( \underline{U}_1 = 7.5 V\underline{/0°} \) und \( \underline{U}_2 = 7.5 V\underline{/120°} \) gelegt ( f = 500 Hz). Berechnen Sie die Spannung \( \underline{U}_3 \).
Aufgabe 3 Stellen Sie die Leitwertfunktion auf. \( R_1 = 560 \Omega, C_1 = 220 nF, R_2 = 100 \Omega, L1 = 20 mH \) Normieren Sie die Leitwertfunktion mit \( G_{bez} = 10 mS \) und \( \omega_{bez} = \frac{1}{L \cdot G_{bez}} \). Erstellen Sie eine Tabelle mit Scheinleitwert und Winkel über der normierten Frequenz. Dazu berechnen Sie die normierte Frequenz, die Scheinleitwerte und die Winkel für f= 0;0.5;1;2;4;8;16 kHz; \( f \rightarrow \infty \). Simulieren Sie die Schaltung mit SPICE.
Aufgabe 4 Bestimmen Sie den Amplitudengang und den Phasengang der auf \( \underline{U}_q(j\omega) \) bezogenen Spannung \( \underline{U}_e(j\omega ) \) für \( R_1 \cdot L_2 = R_2 \cdot L_1 \).

Übung 5:

Aufgabe 1 Pol Nullstellen Bode Diagramm Geben Sie die Pol Nullstellen der Übertragungsfunktion \( \frac{\underline{U}_1}{\underline{U}_q} \) von folgendem Netz wieder. \( R_1 = 100 k\Omega, R_2 = 100 \Omega, R_3 = 1k \Omega, C_1= 2 \mu F\). Zeichnen Sie das Bode Diagramm. Simulieren Sie das Netz mit SPICE. ( \( K = 0.91 , S_{N1} = -5 s^{-1}, S_{P1} = -459 s^{-1} \) )
Aufgabe 2 Pol Nullstellen Bode Diagramm Geben Sie die Pol Nullstellen der Übertragungsfunktion \( \frac{\underline{U}_2}{\underline{U}_1} \) von folgendem Netz wieder. \( R_4 = 50 k\Omega, R_5 = 1 k\Omega, R_6 = 10 k\Omega, L_1 = 50mH\). Zeichnen Sie das Bode Diagramm. Simulieren Sie das Netz mit SPICE. (\( K = 0.167 , S_{N1} = -1.02 \cdot 10^{6} s^{-1}, S_{P1} = -1.87 \cdot 10^{5} s^{-1} \) )
Aufgabe 3 3.1. Geben Sie die Übertragungsfunktion \( \frac{\underline{U}_2}{\underline{U}_1} \), die Pole und Nullstellen von folgendem Netz an. \( R_1 = 30 \Omega, R_2 = 60 \Omega, L_1 = 4 mH, L_2 = 12 mH \). ( \( K = 7500 s^{-1}, S_{N1} = 0 s^{-1}, S_{p1} = -3170 s^{-1} (504 Hz), S_{p2} = -11830 s^{-1} (1882 Hz) \) ) 3.2. Geben Sie die Spannung \( U_ 2 \) für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. ( \( U_2(\omega=0) = 0 V, U_2(\omega \rightarrow \infty) = 0V \))

Aufgabe 4

Gegeben ist folgende Pol-Nullstellen Funktion für den Übertragungsfaktor. Zeichnen Sie das Phasendiagramm.
\( \underline{T}(j\omega) = 10 s \frac{(j \omega + 10^{6}s^{-1})(j\omega + 10^{3} s^{-1})} {j \omega + 10^{4} s^{-1} } \)
Geben Sie die Verstärkung bei f = 0 Hz in dB an.

Übung 6:

Aufgabe 2 Übertragungsfunktion

Berechnen sie den Übertragungsfaktor \( \frac{\underline{U}_A}{\underline{U}_q} \).

Aufgabe 3 SPICE

Gegeben ist folgende SPICE Netzliste. Erstellen Sie den Schaltplan und berechnen sie den Übertragungsfaktor \( \frac{\underline{U}_2}{\underline{U}_1} \).

L1 U1 N001 10m
C1 U2 N001 100p
R1 U2 N001 1000k
R2 U2 0 300
R3 U1 N002 100
V1 N002 0 AC 1 0
.ac dec 10 1 10000000

Klausur SS2010:

Aufgabe 1 1.1 Geben Sie die Periodendauer, Frequenz, Kreisfrequenz, Schwingungsbreite und den Scheitelwert an. 1.2 Berechnen Sie die Kenngrößen der gezeigten Kurve: Gleichwert, Gleichrichtwert, Effektivwert, Schwingungsgehalt, Effektive Welligkeit, und den Riffelfaktor
Aufgabe 2 Es ist folgende Schaltung mit \( R_1 = 1 k\Omega \); \( C_1 = 18 nF, R_2 = 3 k\Omega; L_1 = 32 mH \) gegeben. 2.1. Berechnen Sie den komplexen Eingangswiderstand in R-Form und P-Form für \( f = 125 kHz\). 2.2. Berechnen Sie die Resonanzfrequenz. 2.3. Für welche Widerstandswerte \( R_2 \) gibt es keine Resonanz? Lösung: \( \underline{Z} = \frac{1}{\frac{1}{R_2} + \frac{1}{R_1 + j \omega L_1}} + \frac{1}{j \omega C_1} \) Bei der Umformung eliminiert man Brüche und bringt Unterbrüche auf einen gemeinsamen Nenner bis man nur noch einen Bruch hat. Dann kann man konjugiert komplex erweitern. \( \underline{Z} = \frac{R_2 \left(j \omega L_1 + R_1 \right)} {j \omega L_1 + R_1 + R_2} + \frac{1}{j \omega C_1} \) Ersten Teil konjugiert komplex erweitern: \( \underline{Z} = \frac{R_2 \left(j \omega L_1 + R_1 \right) \left( R_1 + R_2 - j \omega L_1 \right)} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + \frac{1}{j \omega C_1} \) \( \underline{Z} = R_2 \frac{j \omega L_1 \left( R_1 + R_2 - R_1 \right) + R_1 \left( R_1 + R_2 \right) + \omega^2 L_1^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + \frac{1}{j \omega C_1} \) \( \underline{Z} = R_2 \frac{ R_1 \left( R_1 + R_2 \right) + \omega^2 L_1^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + j \left( \frac{\omega L_1 R_2^2 } {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} - \frac{1}{\omega C_1} \right) \) \( \underline{Z} = 2.94 k\Omega + j 279 \Omega = 2957 \Omega \underline{/5.4°} \) Imaginärteil von \( \underline{Z} \) gleich 0 setzen \( Im\{\underline{Z}\} = \frac{ \omega L_1 R_2^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} - \frac{1}{\omega C_1} = 0 \) \( \omega^2 C_1 L_1 R_2^2 = \left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2 \) \( \omega^2 \left(C_1 L_1 R_2^2 - L_1^2 \right) = \left(R_1 + R_2\right)^2 \) \( \omega^2 = \frac{\left(R_1 + R_2\right)^2} {C_1 L_1 R_2^2 - L_1^2} \) \( \omega = \sqrt{\frac{\left(R_1 + R_2\right)^2} {C_1 L_1 R_2^2 - L_1^2}} = s^{-1} \) \( C_1 L_1 R_2^2 - L_1^2 \lt 0 \) \( R_2 \lt \sqrt{\frac{L_1}{C_1}} = 1.33 k\Omega \) Alternativ: \( \underline{Z} = \frac{j \omega C_1 R_2 \left(j \omega L_1 + R_1 \right) + j \omega L_1 + R_1 + R_2} {\left(j \omega L_1 + R_1 + R_2\right) j \omega C_1 } \) Für den komplexen Widerstand ergibt sich für \( \left( j \omega \right)^2 = - \omega^2 \) \( \underline{Z} = \frac{j \omega \left( C_1 R_2 R_1 + L_1\right) - \omega^2 C_1 R_2 L_1 + R_1 + R_2} {j \omega C_1 \left( R_1 + R_2\right) - \omega^2 C_1 L_1 } \) \( \underline{Z} = \frac{j \omega \left( C_1 R_2 R_1 + L_1\right) + \omega^2 C_1 R_2 L_1 - R_1 - R_2} {\omega^2 C_1 L_1 - j \omega C_1 \left( R_1 + R_2\right) } \) Konjugiert komplex erweitern: \( \underline{Z} = \frac{\left( j \omega \left( C_1 R_2 R_1 + L_1\right) + \omega^2 C_1 R_2 L_1 - R_1 - R_2\right) \left(\omega^2 C_1 L_1 + j \omega C_1 \left( R_1 + R_2\right) \right) } {\omega^4 C_1^2 L_1^2 + \omega^2 C_1^2 \left( R_1 + R_2\right)^2 } \) Zähler nach Realteil und Imaginärteil sortieren: \( \underline{Z} = \frac{\left(\omega^2 C_1 R_2 L_1 - R_1 - R_2\right) \omega^2 C_1 L_1 - \omega^2 C_1 \left( R_1 + R_2\right)\left( C_1 R_2 R_1 + L_1\right) + j \left( \omega^3 C_1 L_1 \left( C_1 R_2 R_1 + L_1\right) + \omega C_1 \left( R_1 + R_2\right) \left( \omega^2 C_1 R_2 L_1 - R_1 - R_2 \right)\right)} {\omega^4 C_1^2 L_1^2 + \omega^2 C_1^2 \left( R_1 + R_2\right)^2 } \) Imaginärteil Null setzen: \( \omega^3 C_1 L_1 \left( C_1 R_2 R_1 + L_1\right) + \omega C_1 \left( R_1 + R_2\right) \left( \omega^2 C_1 R_2 L_1 - R_1 - R_2 \right) = 0 \) \( \omega^2 C_1 L_1 \left( C_1 R_2 R_1 + L_1\right) + C_1 \left( R_1 + R_2\right) \left( \omega^2 C_1 R_2 L_1 - R_1 - R_2 \right) = 0 \) \( \omega^2 C_1 L_1 \left( C_1 R_2 R_1 + L_1 + R_2 C_1 \left( R_1+R_2 \right) \right) - C_1 \left( R_1 + R_2\right) \left( R_1 + R_2 \right) = 0 \) Verifikation des Ergebnisses mit LTSPICE In LTSPICE verifiziert man diese Lösung mit einer Stromquelle am Eingang mit 1 A. Mit der AC Simulation wird dann \( \underline{Z} = \frac{\underline{U_1}}{\underline{I}} \) dargestellt. Für die Frequenz 125 kHz liest man bei linearer Skalierung die P-Form ab: 3 kOhm und 5° ab. Mit linker Maustaste (LMT) kann man für die y-Achse 'Nyquist' wählen und die Ortskurve darstellen. Dann bekommt man die R-Form: R = 2.94 kΩ und X = 294 Ω.
Aufgabe 3 3.1. Geben Sie die Pole und Nullstellen der Übertragungsfunktion \( \frac{\underline{U}_1}{\underline{U}_q} \) von folgendem Netz an. \( R_1 = 10 \Omega, R_2 = 2490 \Omega, L = 40 mH, C = 40nF\). 3.2. Geben Sie die Spannung \( \underline{U}_1 \) für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. Lösung: \( \frac{\underline{U}_1}{\underline{U}_q} = \frac{ R_1 + j \omega L_1}{\frac{1}{j \omega C} + R_2 + R_1 + j \omega L_1} \) \( \frac{\underline{U}_1}{\underline{U}_q} = L_1 \frac{\left(j \omega + \frac{R_1}{L_1}\right) j \omega} {(j \omega)^2 L_1 + j \omega (R_1 + R_2) + \frac{1}{C}} \) \( \frac{\underline{U}_1}{\underline{U}_q} = \frac{\left(j \omega + \frac{R_1}{L_1}\right) j \omega} {(j \omega)^2 + j \omega \frac{R_1 + R_2}{L_1} + \frac{1}{C L_1}} \) \( j \omega_{1,2} = \frac{R_1 + R_2}{2 L_1} \pm \sqrt{\frac{(R_1 + R_2)^2}{4 L_1^2} - \frac{1}{C L_1}} \) \( j \omega_{1,2} = \frac{R_1 + R_2}{2 L_1} \pm \sqrt{\frac{(R_1 + R_2)^2}{4 L_1^2} - \frac{1}{C L_1}} \) s_N1 = 0 s_N2 = -250 s^-1 f_sN2 = 39.8 Hz s_P1 = -50000 s^-1 s_P2 = -12500 s^-1 f_sP1 = 7.96 kHz f_sP2 = 2 kHz \( U_1 (\omega = 0) = 0 V \) \( U_1 (\omega \rightarrow \infty) = U_q \) Man kann in LTSPICE gesteuerte Quellen mit einer Laplace-Gleichung, einer Übertragungsfunktion eingeben und so den Ansatz und alle Rechenschritte überprüfen.

Aufgabe 4

Gegeben ist folgende Pol-Nullstellen Funktion für den Übertragungsfaktor. Zeichnen Sie das Bodediagramm (Betrag und Phase).
\( \underline{T}(j\omega) = 8 \frac{j\omega + 200 s^{-1}}{j \omega + 4000 s^{-1}} \)
Geben Sie die Verstärkung bei f = 0 Hz in dB an.

Klausur SS2011:

Aufgabe 1 1.1 Geben Sie die Periodendauer, Frequenz und den Scheitelwert an.(3 Punkte) 1.2 Berechnen Sie den Gleichwert, den Effektivwert und den Schwingungsgehalt. (9 Punkte)
Aufgabe 2 Es ist folgende Schaltung mit \( R_C = 10 \Omega; C = 60 \mu F\), \( R_L = 20 \Omega, L = 2 mH \) gegeben. 2.1. Berechnen Sie den komplexen Eingangswiderstand in P-Form und R-Form für \( \omega = 800 rad/s \). (6 Punkte) 2.2. Berechnen Sie die Resonanzfrequenz. (6 Punkte) 2.3. Für welche Widerstandswerte \( R_ C \) gibt es keine Resonanz? (2 Punkte)
Aufgabe 3 3.1. Geben Sie die Übertragungsfunktion \( \frac{\underline{U}_2}{\underline{U}_1} \), die Pole und Nullstellen von folgendem Netz an. \( R_1 = 20 \Omega, R_2 = 40 \Omega, C_1 = 4 \mu F\), \( C_2 = 12 \mu F\). (13 Punkte) 3.2. Geben Sie die Spannung \( \underline{U}_2 \) für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. (2 Punkte) (Sn1 = 0 s^-1, Sp1 = -1340 s^-1, Sp2 = -19500 s^-1, fn1 = 0 Hz, fp1 = 213 Hz, fp2 = 3.1 kHz)
Aufgabe 4 Gegeben ist folgende Schaltung mit einer linearen Spannungsquelle mit \( U_q = 5 V (f = 400 Hz) \) und \( R_i = 20 \Omega \), die einen Verbraucher mit L = 5.6 mH und \( R_1 = 10 \Omega \) versorgt. Mit Hilfe der Kapazität C soll der Leistungsfaktor 1 werden. 4.1 Bestimmen Sie die Kapazität C. (2 Punkte) 4.2 Bestimmen Sie die komplexe Leistung des Verbrauchers. (3 Punkte) 4.4 Zeichnen Sie die Ortskurve des mit \( R_{bez} = 10 \Omega \) normierten komplexen Verbraucherwiderstandes bestehend aus C, \( R_1 \) und L. (4 Punkte)

Klausur SS2013:

Aufgabe 1 Berechnen Sie den Gleichwert, den Effektivwert und den Schwingungsgehalt. (8 Punkte)
Aufgabe 2 Es ist folgende Schaltung mit \( R_1 = 80 \Omega; C = 4 \mu F, R_2 = 40 \Omega, L = 8 mH \) gegeben. 2.1. Berechnen Sie den komplexen Eingangswiderstand in P-Form und R-Form für \( \omega = 5000 rad/s \). (6 Punkte) 2.2. Berechnen Sie die Resonanzfrequenz. (3 Punkte) 2.3. Für welche Widerstandswerte \( R_2 \) gibt es keine Resonanz? (2 Punkte)
Aufgabe 3 3.1. Geben Sie die Übertragungsfunktion \( \frac{\underline{U}_a}{\underline{U}_e} \), die Pole und Nullstellen von folgendem Netz an. \( R_1 = 20 \Omega, R_2 = 40 \Omega, C_1 = 1 \mu F, L_1 = 4 mH\). (8 Punkte) 3.2. Geben Sie die Spannung \( \underline{U}_a \) für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. (2 Punkte)
Aufgabe 4 Gegeben ist folgende Schaltung mit einer linearen Spannungsquelle mit \( U_1 = 3 V (f = 400Hz) \) und \( R_i = 10 \Omega \), die einen Verbraucher mit \( C = 20 \mu F \) und \( R_2 = 20 \Omega \) versorgt. Bestimmen Sie die komplexe Leistung des Verbrauchers. (4 Punkte)

Aufgabe 5

Gegeben ist folgende Pol-Nullstellen Funktion für den Übertragungsfaktor.
\( \underline{T}(j\omega) = 20 \frac{j\omega + 2 s^{-1}}{(j\omega + 40 s^{-1} ) \cdot (j\omega + 800 s^{-1} )} \)
Zeichnen Sie das Bodediagramm (Betrag und Phase).
Die Teilfunktionen müssen sichtbar sein.
Geben Sie die Verstärkung bei \( \omega = 2 s^{-1} \) in dB an. (5 Punkte)

Element	Wirkwiderstand R	Blindwiderstand X	Wirkleistung P	Blindleistung Q
R	747 Ω	0	35.4 W	0
C	0	-747 Ω	0	-35.4 var
L	0	747 Ω	0	35.4 var

Übungen Grundlagen Elektrotechnik 2

Übung 1: Wechselgrößen

Aufgabe 1: Rechteck Wechselgröße

Aufgabe 2: Wechselgröße

Aufgabe 3 Wechselgrößen

Aufgabe 4 SPICE

Übung 2: Leistung, Grundzweipole, Zeigerdiagramm

Aufgabe 1

Aufgabe 2

Aufgabe 3 Leistung

Aufgabe 4 Leistung

Aufgabe 5 Komplexer Zweipol

Aufgabe 6 Komplexer Zweipol, Leistung

Aufgabe 7

Aufgabe 8

Übung 3: Netze, Resonanz

Aufgabe 1

Aufgabe 2

Aufgabe 3 Komplexer Widerstand

Aufgabe 4 Resonanz

Übung 4:

Aufgabe 1: Komplexer Widerstand und Ortskurve

Aufgabe 2

Aufgabe 3

Aufgabe 4

Übung 5:

Aufgabe 1 Pol Nullstellen Bode Diagramm

Aufgabe 2 Pol Nullstellen Bode Diagramm

Aufgabe 3

Aufgabe 4

Übung 6:

Aufgabe 2 Übertragungsfunktion

Aufgabe 3 SPICE

Klausur SS2010:

Aufgabe 1

Aufgabe 2

Verifikation des Ergebnisses mit LTSPICE

Aufgabe 3

Aufgabe 4

Klausur SS2011:

Aufgabe 1

Aufgabe 2

Aufgabe 3

Aufgabe 4

Klausur SS2013:

Aufgabe 1

Aufgabe 2

Aufgabe 3

Aufgabe 4

Aufgabe 5