Review and Overview
- Figure of Merit for ADCs
- Noise in data converters
- Interfaces
Data converter performance parameters
| ISSC 2008 [1] | VLSI 2012 [2] | VLSI 2013 [3] | ISSC 2014 [4] | |
| Technology [nm] | 90 | 40 | 32 SOI | 40 LP |
| Resolution | 5 | 6 | 6 | 7 |
| Power supply [V] | 1 | 1.1 | 0.85 | 1.1 |
| Sampling Frequency [GS/s] | 1.75 | 3 | 5 | 2.2 |
| Power Consumption [mW] | 2.2 | 11 | 8.5 | 27.4 |
| SNDR @Nyquist [dB] | 27.6 | 33.1 | 30.9 | 37.4 |
| FoMw [fJ/conv step] | 64.5 | 99.3 | 59.4 | 210 |
| FoMs [dB] | 143.5 | 144.4 | 145.6 | 143.3 |
| Core area [mm2] | 0.0165 | 0.021 | 0.02 | 0.052 |
| Calibration | Off chip | Foreground | Off chip | No need |
[1] B. Verbruggen, et al., “A 2.2mW 5b 1.75GS/s Folding Flash ADC in 90nm
Digital CMOS,” ISSCC Dig. Tech. Papers, pp. 252-253, Feb. 2008.
[2] Y.-S Shu, “A 6b 3GS/s 11mW Fully Dynamic ADC in 40nm CMOS with Reduced Number of comparators,” Symp. VLSI Circuits, pp. 26-27, June 2012.VLSI 2012
[3] V. H. -C. Chen and L. Pileggi, “An 8.5mW 5GS/s 6b Flash ADC with Dynamic Offset Calibration in 32nm CMOS SOI,” Symp. VLSI Circuits , pp. 264-265, June 2013.
[4] M. Miyahara, et. al., "22.6 A 2.2GS/s 7b 27.4mW time-based folding-flash ADC with resistively averaged voltage-to-time amplifiers," 2014 ISSCC, San Francisco, CA, 2014, pp. 388-389.
[2] Y.-S Shu, “A 6b 3GS/s 11mW Fully Dynamic ADC in 40nm CMOS with Reduced Number of comparators,” Symp. VLSI Circuits, pp. 26-27, June 2012.VLSI 2012
[3] V. H. -C. Chen and L. Pileggi, “An 8.5mW 5GS/s 6b Flash ADC with Dynamic Offset Calibration in 32nm CMOS SOI,” Symp. VLSI Circuits , pp. 264-265, June 2013.
[4] M. Miyahara, et. al., "22.6 A 2.2GS/s 7b 27.4mW time-based folding-flash ADC with resistively averaged voltage-to-time amplifiers," 2014 ISSCC, San Francisco, CA, 2014, pp. 388-389.
Data converter performance parameters
- Sampling frequency
- Resolution, effective number of bits, signal to noise ratio (ENOB, SNDR)
- Power consumption, power supply
- Publication data
- Commercial data
- Architecture
- Technology: feature size, area
Murmann, ADC Survey https://github.com/bmurmann/ADC-survey
Video: https://www.youtube.com/watch?v=dlD0Jz3d594
Citation:
A figure of merit (FoM) is a useful tool for comparing the conversion efficiency of A/D converters. This presentation reviews the make-up and composition of the most popular FoMs quantifying the tradeoff between ADC speed, resolution and power dissipation. In addition, it investigates the pertaining asymptotes and trends over time. The obtained information allows us to quantify past progress rates and lets us speculate about the future.
A figure of merit (FoM) is a useful tool for comparing the conversion efficiency of A/D converters. This presentation reviews the make-up and composition of the most popular FoMs quantifying the tradeoff between ADC speed, resolution and power dissipation. In addition, it investigates the pertaining asymptotes and trends over time. The obtained information allows us to quantify past progress rates and lets us speculate about the future.
ADC Figure of Merit Conversion
Walden:
\( FOM_{1} = \frac{Power}{f_{S} \cdot 2^{ENOB}} [fJ/conversion step] \)
\( ENOB = \frac{SNDR-1.76}{6.02} \)
Ref: R.H. Walden, "Analog-to-digital converter survey and analysis," IEEE J. Selected Areas Comm., April 1999
Schreier:
\( FOM_{2} = SNR + 10log\left( \frac{f_{S}}{2 P}\right) [dB]\)
R. Schreier and G.C.Termes, Understanding Delta-Sigma Data-Converters, Wiley 2005
\( FOM_{3} = SNDR + 10log\frac{f_{S}}{2 Power} [dB]\)
A.M.A. Ali et al., "A 16-bit 250MS/s IF Sampling Pipelined ADC with background calibration, JSSC, Dec2010
FOM1: Small numbers are better.
FOM2: Large numbers are better.
\( FOM_2 = 10 log(\frac{1}{FOM_1}) \)
This figure of merit takes into account best performance per part.
FOM2: Large numbers are better.
\( FOM_2 = 10 log(\frac{1}{FOM_1}) \)
This figure of merit takes into account best performance per part.
ADC Figure of Merit Architecture
- Area A per feature size F
- Power per voltage VDD
Modified Walden:
\( FOMa_{1} = \frac{Power \cdot A}{f_{S} \cdot 2^{ENOB} \cdot F^2 \cdot VDD^2} [fJ/conversion step] \)
\( ENOB = \frac{SNDR-1.76}{6.02} \)
Ref: R.H. Walden, "Analog-to-digital converter survey and analysis," IEEE J. Selected Areas Comm., April 1999
Modified Schreier:
\( FOMa_{2} = SN(D)R + 10log\left( \frac{f_{S} \cdot VDD^2 \cdot F^2}{2 P \cdot A}\right) [dB]\)
R. Schreier and G.C.Termes, Understanding Delta-Sigma Data-Converters, Wiley 2005
This figure of merit takes the used technology into account.
Relationships
- Frequency and number of bits:
Matching should be better, input capacitance bigger, frequency reduces - Matching: Power grows with 8x per added bit
- Thermal noise: Power grows with 4x per added bit
- Process CV2: Power grows with 2x per added bit
- Feature size: Power, speed
- Architecture: Flash, Pipeline, SAR, sigma delta
Fundamental Limit
Class-B Amplifier, sample and hold C, Brickwall LPF at fsample/2
\( SNR = \frac{\frac{1}{2} \left( \frac{V_{FS}}{2}\right)^2 }{\frac{kT}{C}} \frac{f_S}{f_{snyq}} = \frac{1}{8} \frac{C}{kT} V_{FS}^{2} \frac{f_S}{f_{snyq}} \)
Pmin = I · V = Q · fsample · VDD = C · VFS · fS · VFS
VDD = VFS
\( E_{min} = \frac{P_{min}}{f_{synyq}} = 8 k T \cdot SNR \)
Energy over SNR, energy per bit.
Ref: Hosticka, Proc. IEEE 1985; Vitoz, ISCAS 1990
with:
\( FOM_{2} = SNR + 10log\left( \frac{f_{S}}{2 P}\right) = SNR + 10log\left( \frac{1}{E_{min}}\right) = 10 log\left( \frac{1}{8kT}\right) = 198 dB\)
SNR is power of sine signal divided by noise power.
DAC ADC Measurement
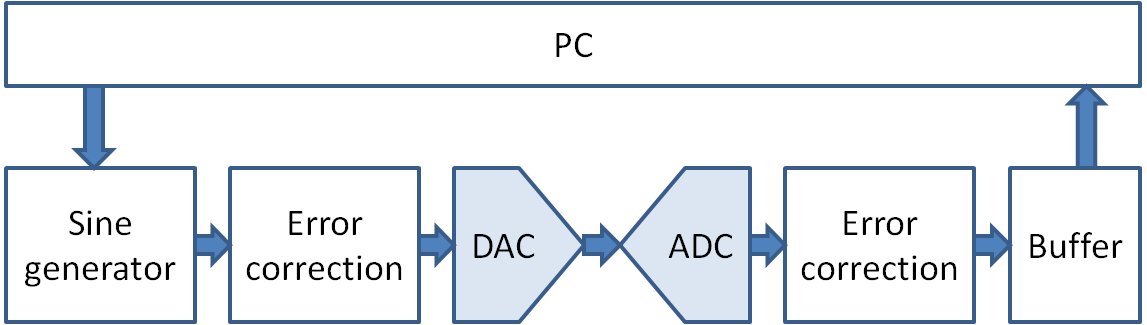
|
DAC: ADC: N: Offset Error: Gain Error: |
Investigations
| DAC Bits | ADC Bits | N | Offset Error | Gain Error | Comment |
| 3 | 3 | 1 | 0 | 0 | Same number of Bits and no error |
| 3 | 5 | 1 | 2 | -20% | DAC is tested by ADC and shows a limited output range |
| 5 | 4 | 1 | 2 | -20% | ADC is tested by DAC and shows a limited output range |
ADC and DAC same number of bits:
Total errors bigger than 1 LSB can be detected.
Offset and gain errors can lead to a reduced number of output codes.
It is not clear if ADC or DAC has errors.
ADC has more bits than DAC:
Only DAC is tested
INL, DNL errors of 2BDAC/BADC · LSB can be detected.
Offset and gain error can lead to a limited output range.
ADC has less bits than DAC:
Only ADC is tested.
INL, DNL errors of 2BADC/BDAC · LSB can be detected.
A range of DAC codes gives the same ADC output code. This is a histogramm test.
General remarks
Taking multiple measurement points per DAC code can look like a histogram test.
Noise can cause multiple ADC codes per DAC code.
A histogram test averages noise out.
Applying an operational amplifier (Opamp) can increase the resolution of ADC or step size of DAC and adding an offset.
Using a voltage divider enables smaller DAC step sizes.
Characterization can then be done using multiple steps for sub ranges with different offsets.
DAC ADC Test Simulation
DAC X4 provides coarse steps, DAC X2 provides fine steps for ADC test.
For high resolution DAC test The DAC ouput can be amplified and an offset applied and the tested with the ADC.
Another possibility for DAC test would be to build a 2 stage multibit pipeline ADC.
For high resolution DAC test The DAC ouput can be amplified and an offset applied and the tested with the ADC.
Another possibility for DAC test would be to build a 2 stage multibit pipeline ADC.
Data Converters: INL, DNL, SNR
Binary weighted
| Error | DNL | INL | SNR | Error correction possible |
| +10% D7 | ||||
| -10% D7 | ||||
| +10% D6 | ||||
| -10% D6 | ||||
| +1% D5 | ||||
| -1% D4 |
Unit element
| Error | DNL | INL | SNR | Error correction possible |
| +10% | ||||
| -10% | ||||
| +1% | ||||
| -1% |
Summary of Interface Electronics
- DAC: (Ladder, R string, Interpolating,) Binary, R2R, C2C, C Serial
- ADC: (Flash, Dual slope,) Pipeline ADC), SAR ADC, Sigma Delta
- Comparator, Amplifier, Switch, Sample and Hold
- Averaging, Interpolating, Serial, parallel
- Offset, gain, INL, DNL, FFT, SNR, test, error correction and diagnosis effort
Calculate INL, DNL (Ramp test, Histogram test)
Analyze a FFT.
Recognize DAC, ADC architecture and calculate transfer curve.
Calculate RC for NBit and fbw for switch and sample and hold.
(Calculate amplifier and comparator requirements (gain, offset))
Analyze a FFT.
Recognize DAC, ADC architecture and calculate transfer curve.
Calculate RC for NBit and fbw for switch and sample and hold.
(Calculate amplifier and comparator requirements (gain, offset))
Summary of Interface Electronics
- Signal chain:
ADC, DAC, measurement setup - DAC and ADC architectures:
Theory, Simulation, LTSPICE circuit, practical circuit, measurement - Sample and Hold
- Switched capacitor circuits
- Tools:
Time analysis, charge analysis, s-plane, z-plane
Static: Transfer chart (ramp and sine), INL, DNL, histogram
Dynamic: FFT, Aliasing, SNR, SFDR, SINAD, jitter, windowing
Calibration, error correction and data analysis - Oversampling and signal to noise
- Design and physical limits:
Frequency, resolution ENOB, power - Competencies:
Research the internet
One solution first and then improve
Only a tested circuit works
Steps from theory to working circuit