Interface Electronics13 Advanced Sigma Delta Oversampling ADCProf. Dr. Jörg Vollrath12 Sigma Delta ADC |
Video Lecture: 13 Oversampling Sigma Delta ADC 9.12.2020
|
Länge: |
0:0:0 Oversampling ADC 0:0:47 First order sigma delta 0:2:1 Increasing signal to noise with oversampling 0:8:47 Averaging 0:12:15 Example:100Mhz Clock, 100kHz bandwidth, 10-bit sigma-delta ADC 0:16:45 OSR=fCLK/2/fbw 0:19:27 Graph Increasing number of bits with oversampling 0:24:41 Oversampling with 1000 0:27:27 Digital droop filter 0:32:4 Problems with sigma delta modulator 0:33:7 Duty cycle and overshoot 0:35:17 DC signal and noise signal in band of interest 0:39:7 Switched capacitor circuit 0:42:22 Average current comparison 0:47:17 Simulation of SC circuit 0:49:37 Benefits and drawbacks 0:51:47 2 non overlapping clocks 0:53:27 Switched capcitor integrator 0:54:35 Second order switched capacitor circuit 0:56:12 Stability and Cascaded sigma delta (2-1-MASH) 1:2:37 Details, Comparator E(z), 1:5:7 Analog, digitized analog and digital signals 1:6:47 Integrator and switched capcitor circuit 1:17:12 z-Elements in digital domain 1:18:59 2-1 MASH sigma delta circuit 1:20:47 Jupyter notebook sigma delta 1:23:57 Delay, latency |
Review and Overview
Review:- Objectives sigma delta converter
- Oversampling, filter, aliasing, speed and resolution
- History of oversampling
- Sigma Delta converter architecture
- Passive 1st order sigma delta converter:
Schematic, SPICE, signal example, RC, simulation and filter
- Active: continous time realization (CT)
- Cascaded (MASH)
- Active: switched capacitor realization (SC)
- CIFB architecture
Droop compensating FIR filter
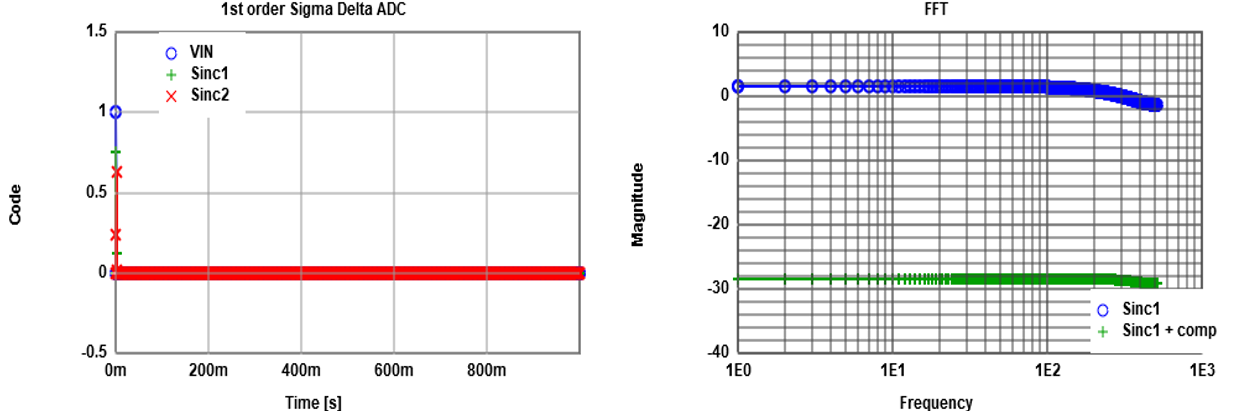
The graphs are generated by 1st order passive sigma delta JavaScript simulator.
Using a pulse input the FFT shows the transfer function of the system.
Droop of the signal can be seen for higher frequencies (blue curve).
The filter can compensate for part of it (green curve).
|
An droop compensating FIR Filter
[ http://www.cypress.com/file/123171/download ]
with a function: \( out(i) = \frac{-1}{K -2} in(i) + \frac{K}{K -2} in(i-1) + \frac{-1}{K -2} in(i-2) \) can be activated. This filter function can be implemented in an FPGA employing shift, add, subtract (using 2s complement) and multiply. Fractions are normalized with the word width of the signal. K values can be taken from the link above.
|
FIR filter block diagram:
 |
Experiments:
Show transfer function: Number of periods = 0, SINC1, SINC2, + comp FIR
Show transfer function: Number of periods = 0, SINC1, SINC2, + comp FIR
Sigma Delta ADC basic
Input parameters:Sample frequency: fclk
Bandwidth: fbw
Number of Bits: B
The ratio \( \frac{f_{clk}}{2 \cdot f_{bw}} = OSR = K \) is called oversampling ratio.
The sigma delta converter can have an order of 1 or higher.
The electric circuit has one RC time constant per order.
The ADC needs a filter and a decimator to generate the final output stream.
Depending on the input parameters, the order (RC) and filter has to be found.
High order sigma delta modulators can give low OSR or high resolution needing more complicated filters.
Sigma Delta ADC Examples
- Can a 10-bit 100kHz sigma delta ADC realized using a 100 MHz clock?
- How much resolution is gained by averaging 1024 values?
Problems with Sigma Delta ADCs
- Tones in first order sigma delta modulator
- Offset is directly transfered to the output
- Mismatch causing gain error and non linearity
- Feedback DAC:
Pulsewidth, offset, Shape
Tone: negative value -0.651 for period generates a DC level.
Ramp test change 50% duty cycle (55%) or 0% overshoot (5%).
A second order passive Sigma Delta ADC
A second order active Sigma Delta ADC
An FFT with 8192 points can be made and VD can be extracted with
Read Raw File
. Start time 0; Stop time 81.92E-6; Time step 10E-9
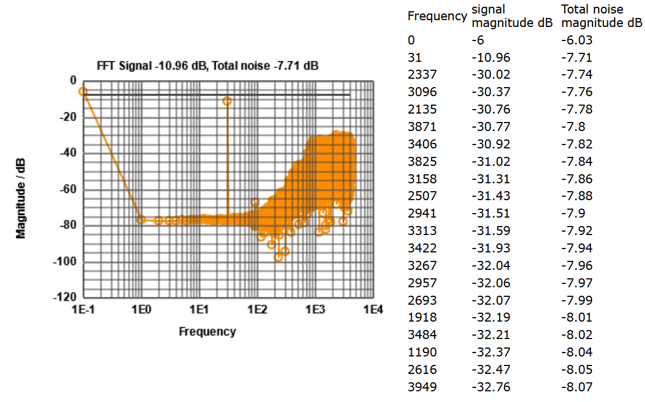
Figure: FFT of 1-Bit output signal.
Oversampling rate:
\( OSR = \frac{f_{CLK}}{2 \cdot f_{BW}} = f_{CLK} \cdot 2 \cdot 2 \pi R \cdot C = 100 MHz \cdot 1.5 \mu s = 150 \)
Between frequencies 100 and 1000 the noise increases by 50 dB as expected.
The corner freqeuncy of 100 is determined by the R = 5 kΩ and C = 10 pF values.
Frequency of 1 has a period T = 81.920 us and a frequency of fmin = 11.22 kHz.
\( f_{3dB} = \frac{1}{2 \pi R C} = \frac{1}{2 \pi 5 k\Omega 10 pF} = 3.2 MHz \).
Normalized
\( f_{3dBNorm} = \frac{f_{3dB}}{f_{min}} = 300 \).
The bigger RC is, the smaller gets the amplitude at the comparator.
For large RC values instability can be seen.
The comparator has to be more sensitive and has to have less offset.
. Start time 0; Stop time 81.92E-6; Time step 10E-9

Figure: FFT of 1-Bit output signal.
Oversampling rate:
\( OSR = \frac{f_{CLK}}{2 \cdot f_{BW}} = f_{CLK} \cdot 2 \cdot 2 \pi R \cdot C = 100 MHz \cdot 1.5 \mu s = 150 \)
Between frequencies 100 and 1000 the noise increases by 50 dB as expected.
The corner freqeuncy of 100 is determined by the R = 5 kΩ and C = 10 pF values.
Frequency of 1 has a period T = 81.920 us and a frequency of fmin = 11.22 kHz.
\( f_{3dB} = \frac{1}{2 \pi R C} = \frac{1}{2 \pi 5 k\Omega 10 pF} = 3.2 MHz \).
Normalized
\( f_{3dBNorm} = \frac{f_{3dB}}{f_{min}} = 300 \).
The bigger RC is, the smaller gets the amplitude at the comparator.
For large RC values instability can be seen.
The comparator has to be more sensitive and has to have less offset.
Switched capacitor circuits
|
Source: Baker, Mixed signal design, Fig2.35 |
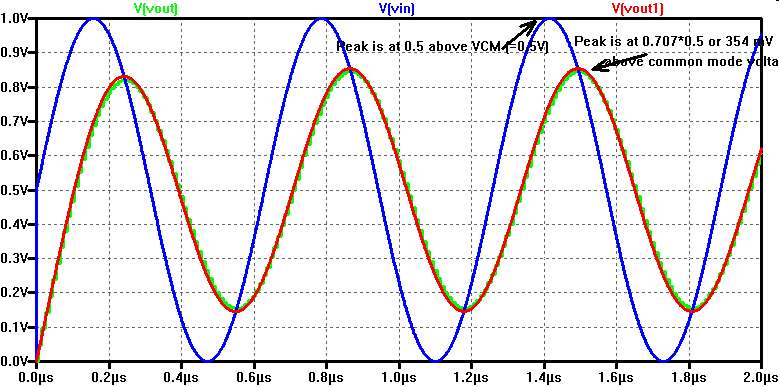  |
In switched capacitor circuits resistors can be replaced by capacitances.
The frequency of the non overlapping clock determines the value.
Capacitances can be fabricated with high accuracy and are less temperature dependent than resistors.
The simulation is done with ideal switches.
Comparison to resistor:
What is the average current?
dV = Vin - Vout
CI · dV = Q = Iavg · dt
\( I_{avg} = \frac{C_{I} \cdot dV}{dt} = C_{I} f dV = \frac{1}{R} dV = G dV\)
CI f = 1p · 100MHz = 0.1 mS = G
z-domain:
\( H_{RC}(z) = \frac{Y(z)}{X(z)} = \frac{1-a}{1-az^{-1}} \)
Reference: Take the RC Low-Pass Filter to the Z-Domain
The frequency of the non overlapping clock determines the value.
Capacitances can be fabricated with high accuracy and are less temperature dependent than resistors.
The simulation is done with ideal switches.
Comparison to resistor:
What is the average current?
dV = Vin - Vout
CI · dV = Q = Iavg · dt
\( I_{avg} = \frac{C_{I} \cdot dV}{dt} = C_{I} f dV = \frac{1}{R} dV = G dV\)
CI f = 1p · 100MHz = 0.1 mS = G
z-domain:
This is a delay element.
Vout(n) · (CI + CF) = Vout(n-1) CF + Vin(n) CI
(CI + CF) Vout(z) = CF z-1 Vout(z) + CI Vin(z)
\( Vout(z) = \frac{CF}{(CI + CF)} z^{-1} Vout(z) + \frac{CI + CF - CF}{CI+CF} Vin(z) \)
\( a = \frac{CF}{CI + CF}\)
\( Vout(z) = a z^{-1} Vout(z) + (1-a) Vin(z) \)
\( Vout(z) (1 - a z^{-1}) = (1-a) Vin(z) \)
\( a = e^{-\frac{1}{ R C_F f}} = e^{-\frac{C_I}{C_F}} \)Vout(n) · (CI + CF) = Vout(n-1) CF + Vin(n) CI
(CI + CF) Vout(z) = CF z-1 Vout(z) + CI Vin(z)
\( Vout(z) = \frac{CF}{(CI + CF)} z^{-1} Vout(z) + \frac{CI + CF - CF}{CI+CF} Vin(z) \)
\( a = \frac{CF}{CI + CF}\)
\( Vout(z) = a z^{-1} Vout(z) + (1-a) Vin(z) \)
\( Vout(z) (1 - a z^{-1}) = (1-a) Vin(z) \)
\( H_{RC}(z) = \frac{Y(z)}{X(z)} = \frac{1-a}{1-az^{-1}} \)
Reference: Take the RC Low-Pass Filter to the Z-Domain
Switched capacitor Integrator
Capacitance C1 has charge Q1.
Q1(n) = C1 * Vin
Q2(n) = Q2(n-1) + Q1(n-1)
C2 Vout(n) = C2 Vout(n-1) + C1 Vin(n-1)
C2 Vout(z) = C2 z-1 Vout(z) + C1 z-1 Vin(z)
C2 Vout(z)(1- z-1) = C1 z-1 Vin(z)
\( Vout(z) = \frac{C1}{C2} \frac{z^{-1}}{1-z^{-1}} Vin(z) \)
Vout(z) = H(z) · Vin(z)
\( H(z) = \frac{C1}{C2} \frac{z^{-1}}{1-z^{-1}} = \frac{C1}{C2} \frac{1}{z-1}\)
Q1(n) = C1 * Vin
Q2(n) = Q2(n-1) + Q1(n-1)
C2 Vout(n) = C2 Vout(n-1) + C1 Vin(n-1)
C2 Vout(z) = C2 z-1 Vout(z) + C1 z-1 Vin(z)
C2 Vout(z)(1- z-1) = C1 z-1 Vin(z)
\( Vout(z) = \frac{C1}{C2} \frac{z^{-1}}{1-z^{-1}} Vin(z) \)
Vout(z) = H(z) · Vin(z)
\( H(z) = \frac{C1}{C2} \frac{z^{-1}}{1-z^{-1}} = \frac{C1}{C2} \frac{1}{z-1}\)
Second order active switched capacitor Sigma Delta modulator
|
Source: Baker, Mixed signal design, Fig 7.29 |
First order SC sigma delta:
\( Vout(z) = E(z) + \frac{1}{z-1} (Vin(z) - Vout(z)) \)
\( Vout(z) \left( 1 + \frac{1}{z-1} \right) = E(z) + \frac{1}{z-1} Vin(z) \)
\( Vout(z) \frac{z}{z-1} = E(z) + \frac{1}{z-1} Vin(z) \)
\( Vout(z) = \frac{z-1}{z} E(z) + \frac{1}{z} Vin(z) \)
\( Vout(z) = (1-z^{-1}) E(z) + z^{-1} Vin(z) \)
Second order SC sigma delta:
\( Vout(z) = E(z) + \frac{1}{z-1} (Vop1(z) - Vout(z)) \)
\( Vout(z) = E(z) + \frac{1}{z-1} \left[ \left( Vin(z)-Vout(z)\right)\frac{1}{z-1} - Vout(z) \right] \)
\( Vout(z) (1 + \frac{1}{z-1} + \frac{1}{(z-1)^{2}}) = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) (\frac{z}{z-1} + \frac{1}{(z-1)^{2}})= E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) \frac{z(z-1) + 1}{(z-1)^{2}} = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) = \frac{(z-1)^{2}}{z(z-1) + 1} E(z) + \frac{1}{z(z-1) + 1} Vin(z) \)
\( Vout(z) = \frac{(1-z^{-1})^{2}}{(1-z^{-1}) + z^{-2}} E(z) + \frac{z^{-2}}{(1-z^{-1}) + z^{-2}} Vin(z) \)
Second order SC sigma delta:
\( Vout(z) = E(z) + \frac{1}{z-1} Vop1(z) \)
\( Vout(z) = E(z) + \frac{1}{(z-1)^2} \left( Vin(z)-Vout(z)\right) \)
\( Vout(z) (1 + \frac{1}{(z-1)^{2}}) = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) \frac{(z-1)^{2}+1}{(z-1)^{2}})= E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) = \frac{(z-1)^{2}}{(z-1)^{2}+1} E(z) + \frac{1}{(z-1)^{2}+1} Vin(z) \)
\( Vout(z) = \frac{(1-z^{-1})^{2}}{(1-z^{-1})^{2} + z^{-2}} E(z) + \frac{z^{-2}}{(1-z^{-1})^{2} + z^{-2}} Vin(z) \)
\( Vout(z) = E(z) + \frac{1}{z-1} (Vin(z) - Vout(z)) \)
\( Vout(z) \left( 1 + \frac{1}{z-1} \right) = E(z) + \frac{1}{z-1} Vin(z) \)
\( Vout(z) \frac{z}{z-1} = E(z) + \frac{1}{z-1} Vin(z) \)
\( Vout(z) = \frac{z-1}{z} E(z) + \frac{1}{z} Vin(z) \)
\( Vout(z) = (1-z^{-1}) E(z) + z^{-1} Vin(z) \)
Second order SC sigma delta:
\( Vout(z) = E(z) + \frac{1}{z-1} (Vop1(z) - Vout(z)) \)
\( Vout(z) = E(z) + \frac{1}{z-1} \left[ \left( Vin(z)-Vout(z)\right)\frac{1}{z-1} - Vout(z) \right] \)
\( Vout(z) (1 + \frac{1}{z-1} + \frac{1}{(z-1)^{2}}) = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) (\frac{z}{z-1} + \frac{1}{(z-1)^{2}})= E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) \frac{z(z-1) + 1}{(z-1)^{2}} = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) = \frac{(z-1)^{2}}{z(z-1) + 1} E(z) + \frac{1}{z(z-1) + 1} Vin(z) \)
\( Vout(z) = \frac{(1-z^{-1})^{2}}{(1-z^{-1}) + z^{-2}} E(z) + \frac{z^{-2}}{(1-z^{-1}) + z^{-2}} Vin(z) \)
Second order SC sigma delta:
\( Vout(z) = E(z) + \frac{1}{z-1} Vop1(z) \)
\( Vout(z) = E(z) + \frac{1}{(z-1)^2} \left( Vin(z)-Vout(z)\right) \)
\( Vout(z) (1 + \frac{1}{(z-1)^{2}}) = E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) \frac{(z-1)^{2}+1}{(z-1)^{2}})= E(z) + \frac{1}{(z-1)^{2}} Vin(z) \)
\( Vout(z) = \frac{(z-1)^{2}}{(z-1)^{2}+1} E(z) + \frac{1}{(z-1)^{2}+1} Vin(z) \)
\( Vout(z) = \frac{(1-z^{-1})^{2}}{(1-z^{-1})^{2} + z^{-2}} E(z) + \frac{z^{-2}}{(1-z^{-1})^{2} + z^{-2}} Vin(z) \)
Cascaded (2-1-MASH) Sigma Delta ADC
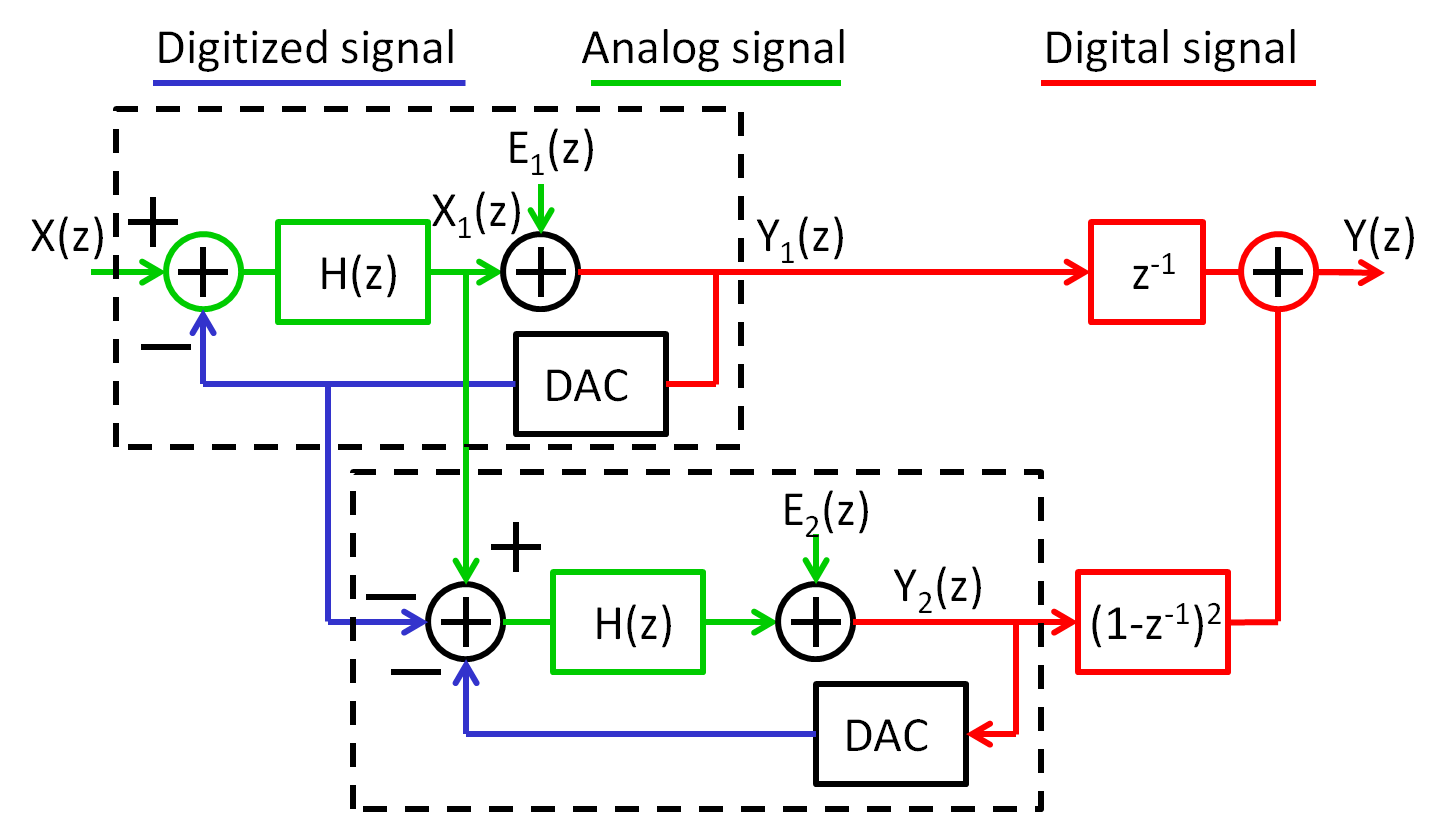
Idea
Quantify digitalization error further and correct in digital domain.
The signal and noise transfer function for a 2-1 MASH sigma delta modulator can be calculated:
\( Y_{1}(z) = z^{-2}\cdot X(z) + (1-z^{-1})^2\cdot E_{1}(z) \Rightarrow *z^{-1}\)
\( Y_{2}(z) = z^{-1}\cdot ( E_{1}(z)) + (1-z^{-1}) \cdot E_{2}(z) \Rightarrow *(1-z^{-1})^2 \)
\( Y(z) = z^{-1}\cdot Y_{1}(z) - (1-z^{-1})^2\cdot Y_{2}(z)\)
\( Y(z) = z^{-3}\cdot X(z) + z^{-1} \cdot (1-z^{-1})^2\cdot E_{1}(z) - z^{-1}\cdot (1-z^{-1})^2\cdot E_{1}(z) + (1-z^{-1})^{3} \cdot E_{2}(z)\)
The \(E_{1}(z)\) terms cancel out:
\( Y(z) = z^{-3}\cdot X(z) - (1-z^{-1})^{3} \cdot E_{2}(z)\)
Brandt, Wooley, A 50-MHz Multibit Sigma Delta Modulator
for 12b 2-MHz A/D Conversion, JSSC, p.1746-1756, Dec 1991
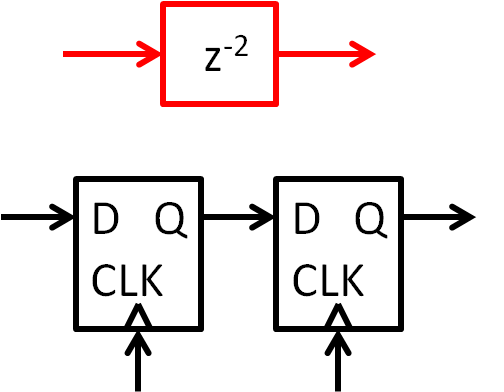
Digital z-Elements
|
_2.png)
|
JavaScript, C: |
JavaScript, C: |
VHDL: |
VHDL: |
What bit width is needed?
What happens if bit width is increased?
What happens if bit width is increased?
A 2-1 Mash Sigma Delta ADC Circuit
Source: MSD, Baker Fig 7.58Next
Next: 14 Figure of merit and summaryToDo:
"Circuit implementation of the transfer function", Akio Kitagawa, Kanazawa University
Sigma Delta iPhyton notebooks
http://www.python-deltasigma.io/- Synthesis of a Noise Transfer Function (NTF),
- Simulation of Delta Sigma modulators,
- Realization and dynamic range scaling,
- Audio demo of mod1 and mod2 and audio file, right click, "Save as..." to download,
- Simulation of a 2-2 MASH cascade,
- Synthesis of a 5th-order, low-pass modulator,
- Synthesis of an 8th-order, band-pass modulator,
- Synthesis of a continuous-time lowpass modulator.
- Synthesis and simulation of a 4th-order bandpass quadrature modulator.
References
"Circuit implementation of the transfer function", Akio Kitagawa, Kanazawa University| Reference | [1] | |
| History | no | |
| Schematic | 1. order passive | no |
| Simulation | Full system | no |
| Digital Filter | z-Plane | no |
| Digital Filter | Schematic | no |
| Digital Filter | VHDL | no |
| Practical Circuit | no | |
| Measurement Results | no | |
| Performance Data | B, fC, fCLK, P |