Laboratory 4: Measuring a 10 Bit R2R DAC

Task:

 Nachgeladener SPICE Text 

1. Measure the resistance value of each resistor with a multi meter.
   
   Solution:
   
   There are only 200kΩ and 100kΩ resistors with 0.1% (200 Ω ; 100 Ω) accuracy available. The resistance of wiring is well below the needed tolerance (100 Ω). The accuracy is 1/1000 and barely sufficient for 10 Bit.
   A typical student measurement is shown below:
   

   Name	R17	R18	R1	R3	R5	R7	R9	R11	R13	R15	R30
   R [kΩ]	200	199.9	199.8	199.8	199.9	200	199.8	200	199.9	199.9	199.8

   Name	R19	R2	R4	R6	R8	R10	R12	R14	R16
   R [kΩ]	99.9	99.9	99.9	99.9	99.9	99.9	99.8	99.9	99.9

   For 0.1% tolerance the values should be between 200.20 and 199.80 kΩ and 100.10 and 99.90 kΩ. The value of 99.8 kΩ is below specification. The accuracy of the multimeter is barely ok. The reported values should have more than 4 digits.
   
   
2. What is the Offset, maximum voltage and LSB of the DAC?
   Start the pattern generator. Create a bus with D0..D9. Select a binary counter with push pull (PP) drivers. Select a frequency of 1kHz under parameter for the counter.
   Make sure that the settling time of the signal is ok for a full level transition.
   Since the oscilloscope has only 10-Bit resolution, you have to do multiple measurements.
   Choose a vertical range of 50 mV/div. Set the Trigger to Channel 1 Rising.
   Use the full vertical range of the oscilloscope to minimize error.
   Channel 1 should show the output voltage, channel 2 and 3 should show D0 and D6.
   Each measurement should give you data for 100 codes each having 80 values.
   For a 10-Bit counting frequency of 1 kHz you have a time base of 10ms/div.
   Export the measurement values (OSC1), D0 (OSC2) and D6 (OSC3) using the Export function. You can use D0, and D6 to synchronize your measurements with the input code.
   Calculate the average output voltage per code using 64 values omitting output voltage values during settling time.
   
   Solution:
   
   The pattern generator for the ramp is shown below:
   
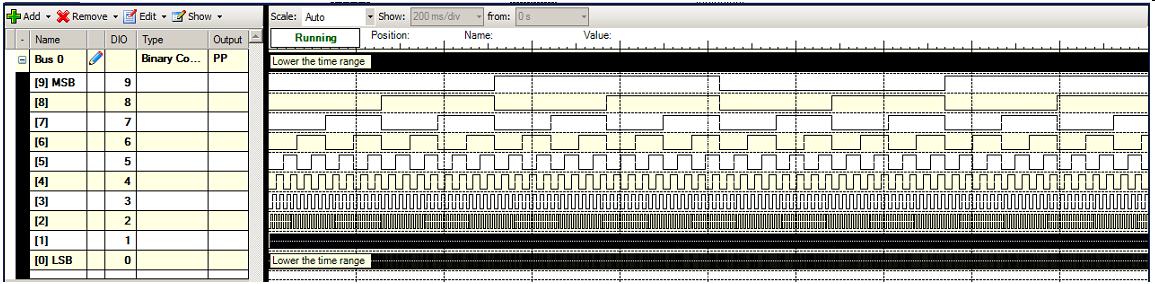
   A typical functional screen shot is also shown:
   
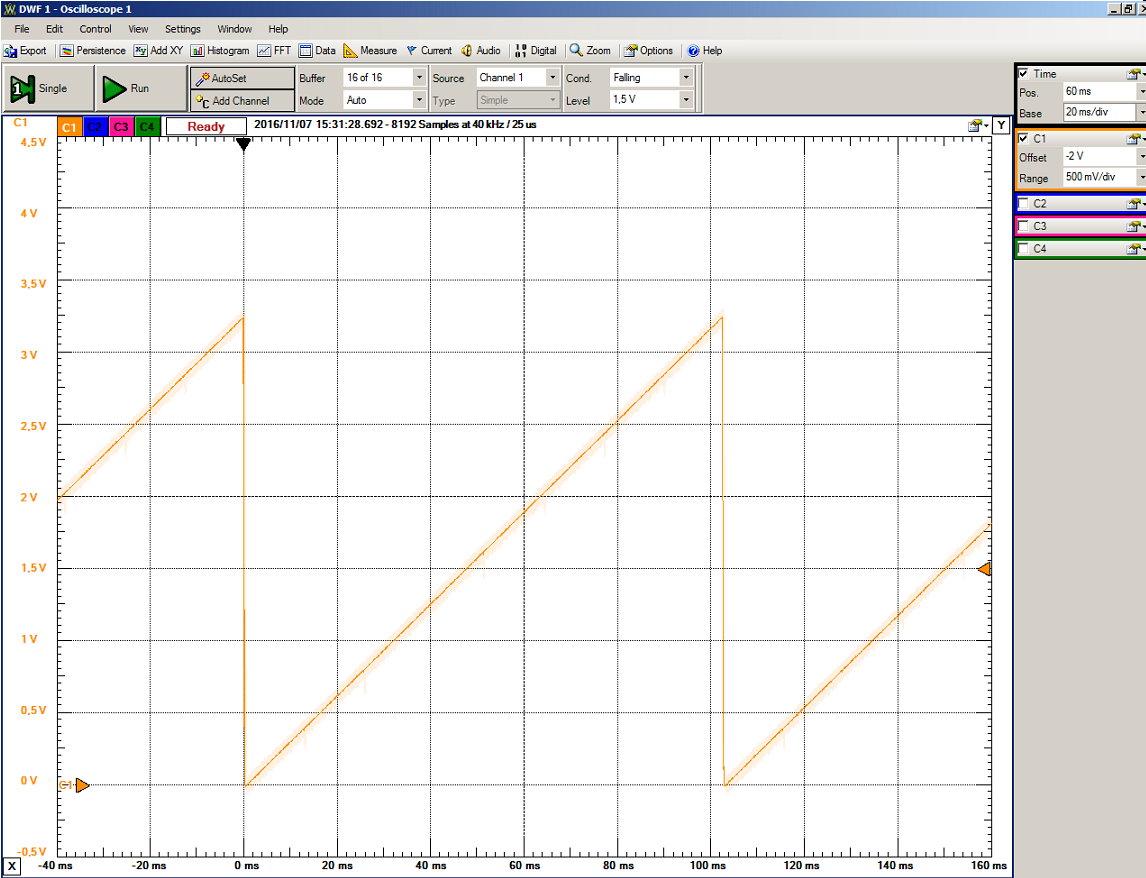
   The y axis shows a range of 5 V. Having a 10-Bit ADC at the oscilloscope this would give a resolution of 5V/1024 = 5mV which is not sufficient for the 10-Bit DAC.
   
   The challenge is to measure 1024 values with enough accuracy in a limited time frame.
   
   The Vout(000) was measured as: Vout(000) = 5.7588 mV. (Offset)
   The Vout(3FF) was measured as: Vout(3FF) = 3.2516 V. (Maximum voltage)
   Both values have to have enough accuracy to calculate a correct LSB with at least 4 digits. Using less digits results in a increasing or decreasing INL because of accumulating rounding error when calculating the ideal curve by summing up LSB.
   
   \( LSB = \frac{3.2516 V - 5.7588 mV}{2^{10}-1 } = 3.1729 mV \)
   
   
   
3. Measure and calculate INL and DNL using Excel or Matlab.
   Here is one way to do it:
   Copy the values to Excel. Create a new column "count" with the current count of the code 0..102.
   Mask the settling time by adding another column "mask" having an "x" only if the count of the 10 last values is stable.
   Insert a pivot table with a "mask" filter, rows; count and values average C1 (V), minimum C1 (V), maximum C1 (V) and average of C3 (V).
   Process your data and make a graph of INL and DNL.
   
   
   Solution:
   
   Normally first a typical partial oscilloscope picture should be shown with the limited y-axis and the time scale. Starting at the beginning of the ramp can show the settling time, noise and stairs.
   
   
   
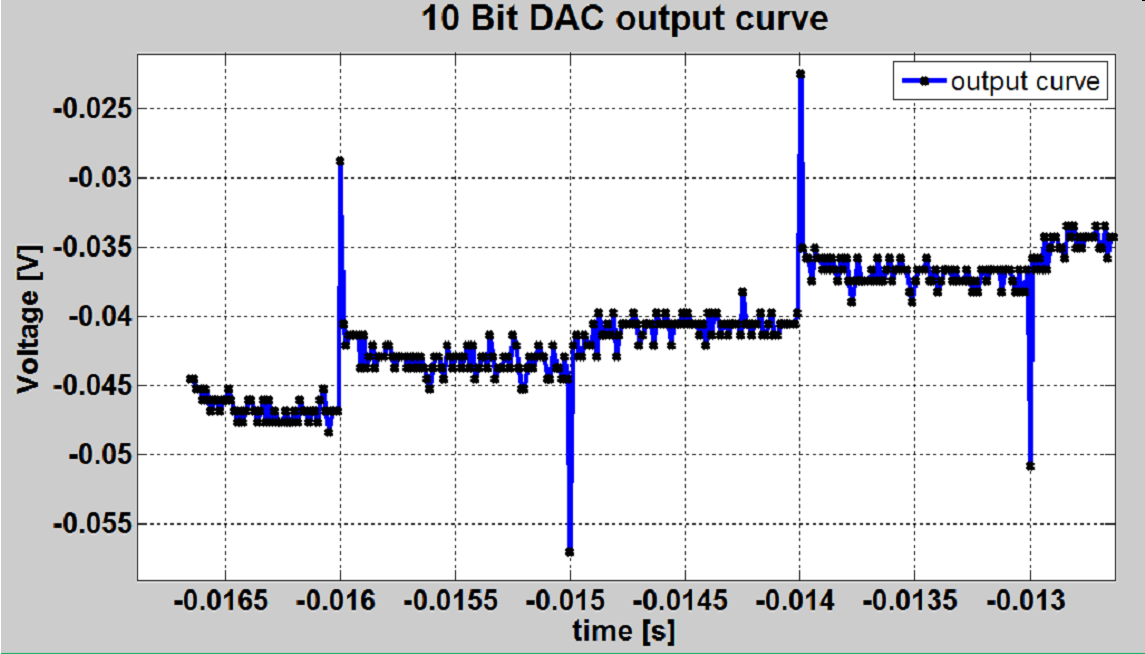
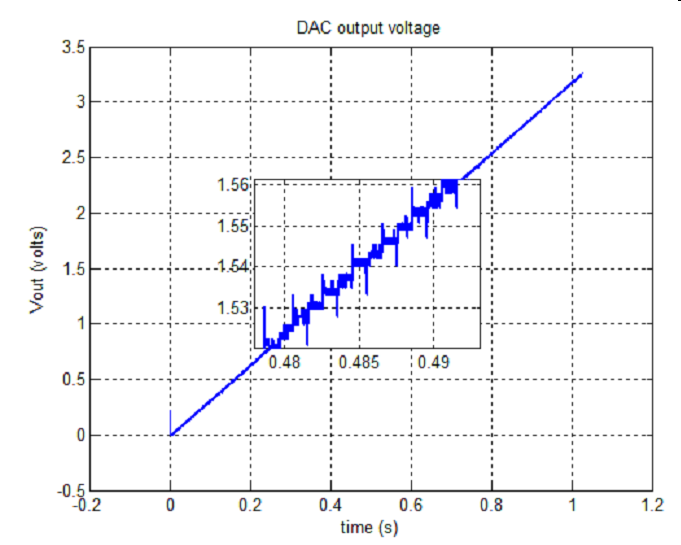
   This example zooms around 1.5V in the combined graph. Combining measurements is difficult to have no gaps and no overlap between measurements to allow correct DNL and INL calculation.
   
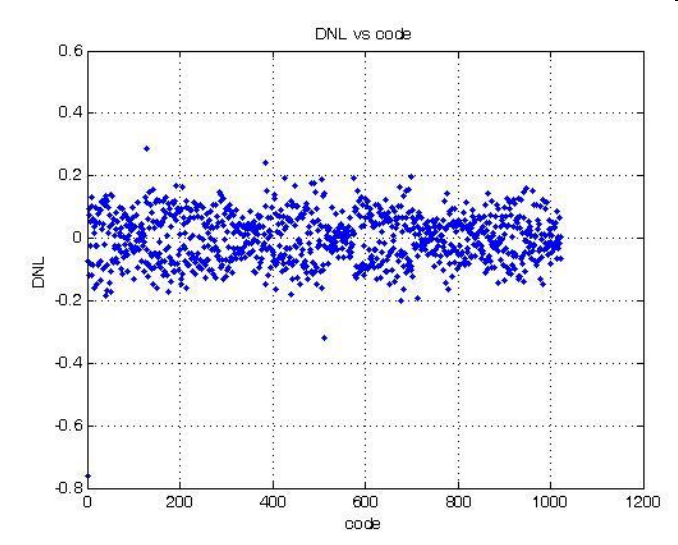
   The DNL shows a nice random distribution below 0.5 LSB.
   
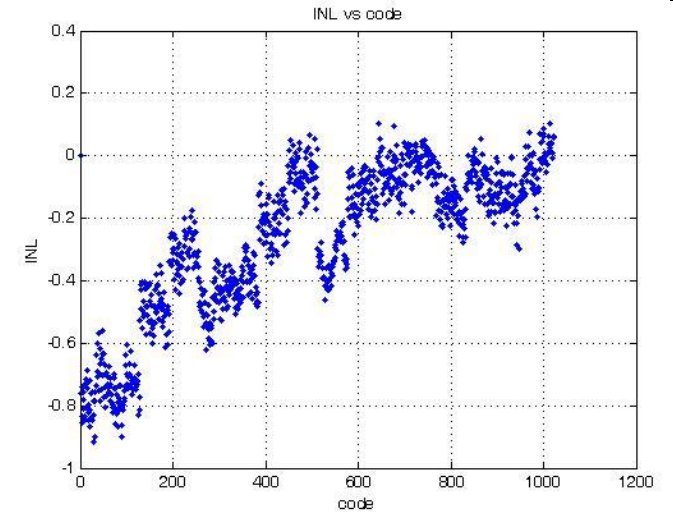
   The INL starts with -0.8 LSB and ends with 0 LSB. It should start at 0 LSB.
   Jumps can be seen in INL which are also single high points in DNL graph.
   These jumps can be either attributed to errors in the DAC because of resistance value tolerance or due to measurement errors when changing trigger, offset and range at the oscilloscope.
   Resistance value tolerance will show up at transitions of 511/512, 255/256 and 767/768 and so on.
   An steady increase or decrease of INL is due to errors in LSB value or accuracy.
   
   
4. Can you improve the INL and DNL of the transfer characteristic by adding resistors?
   
   
   Solution:
   
   If there is a step which is to low or to high, small series resistance can be added.
   Normally this happens first at the MSB.
   
   
5. Measure the improved circuit.
   
   Solution:
   
   
   
6. Change the frequency of the counter and the sequence of the counting and observe the result. Measure settling time. What is the maximum operating frequency?
   
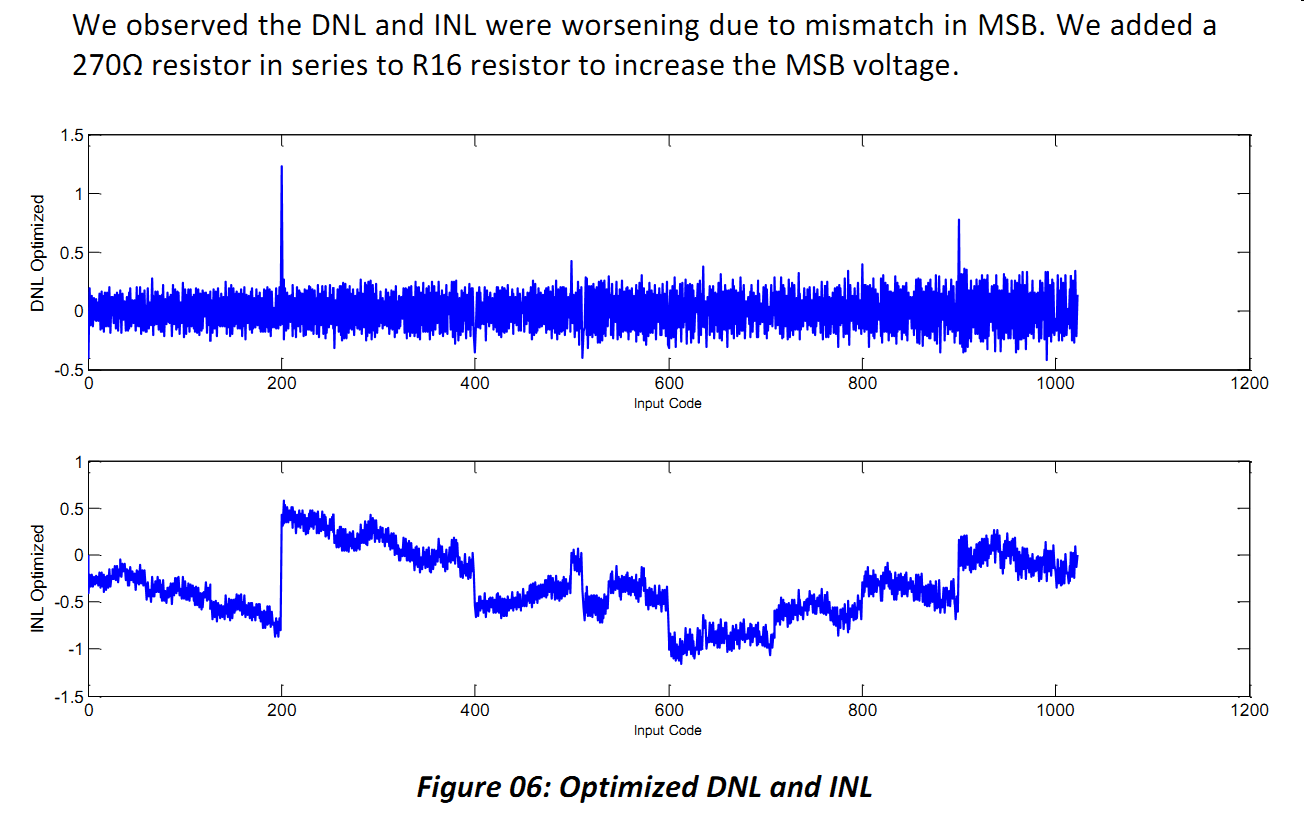
   Solution:
   
   The settling time is measured for full scale and mid level transitions:
   000 -> 3FF
   3FF -> 000
   1FF -> 200
   200 -> 1FF
   Settling times are measured until the output signals stays inside the 1/2 LSB bound error.
   The full scale settling time should be approximated by measuring the time t1 reaching 50% level and applying the equation:
   \( t_{settling} = (B+1) \cdot t_1 \)
   
   
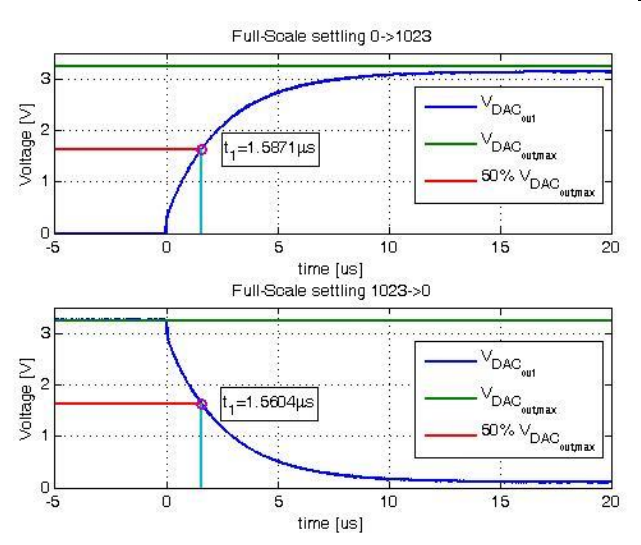
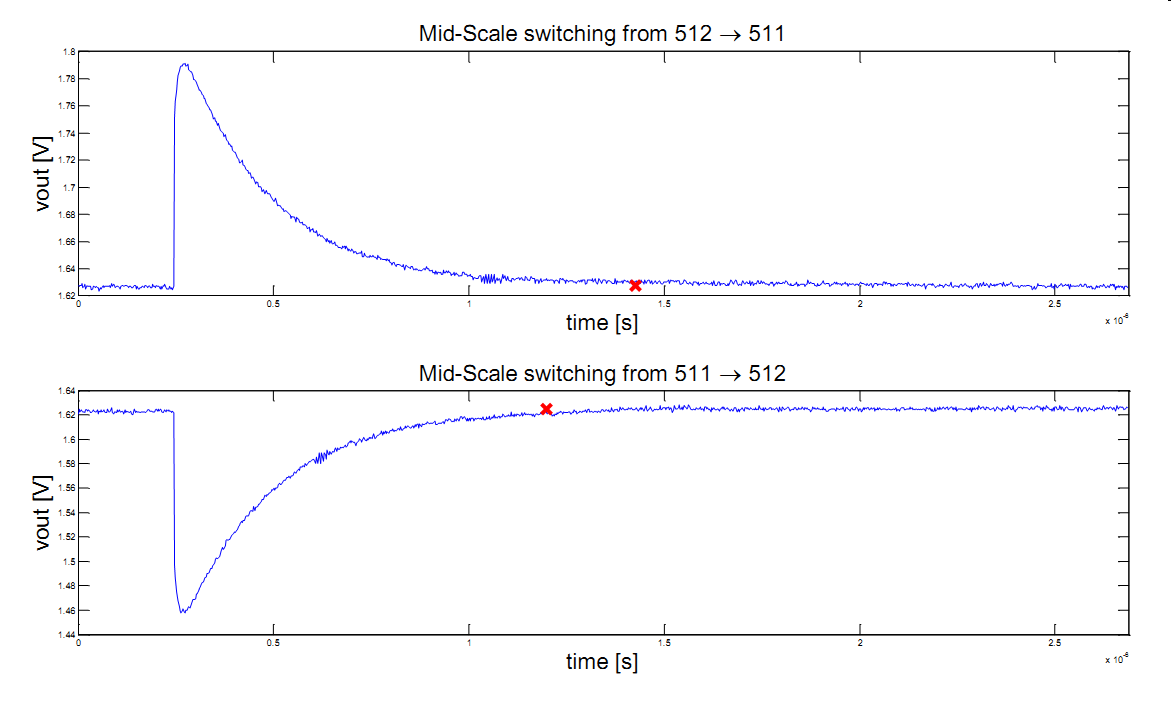
   Typical values for setttling times are:
   20 µ ..500 µs
   Maximum frequency is therefore:
   2 kHz .. 50 kHz
   Comparing measurements using 1/2 LSB error for full level with approximation by using 50% range, show that the approximation underestimates settling times by a factor of 10.
   
   
   
7. Use a digital sine input and measure signal to noise ratio using a fft. Import 10Bit_Sine43Periods.csv into the pattern generator of the Electronic Explorer.
   Measure with different frequencies and input voltage ranges.
   Exchange 2 data lines and measure the impact.
   
   Solution:
   
   A FFT needs a power of 2 number of samples. With the Electronic Explorer 16 k samples are possible.
   A prime number of input periods should be present during this time to prevent bleeding.
   Since the Electronic Explorer has a 10 Bit ADC the signal to noise ratio will be less than \( SNR = 10 \cdot 6.02 dB + 1.76 dB = 62 dB \)
   Estimations of level on a log or dB scale are difficult, since peaks contribute a lot more to the total noise level.
   The number of FFT points N_FFT distributes noise and reduces the noise level by:
   \( 10 \cdot log\frac{N_{FFT}}{2} \)
   16 k samples will reduce the noise level by 40 dB.
   
   To avoid distortion each sampling point from the oscilloscope should take a maximum of one output sample.
   Otherwise a sawtooth signal is added to the sine signal and harmonics will occur.
   
   A typical oscilloscope picture of a student group is shown:
   
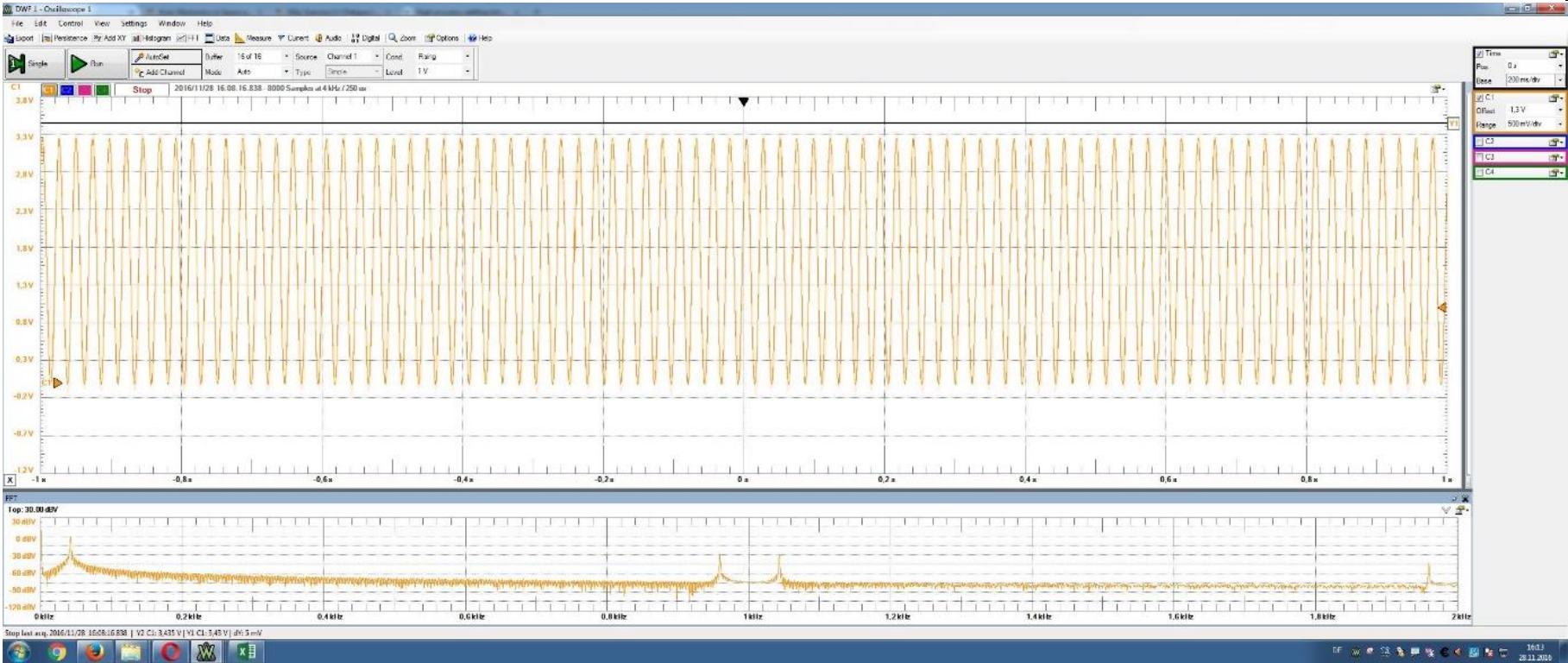
   Measurement time 2s, 80.x periods (Bleeding), oscilloscope sampling time: 2s/16k = 62 us, Pattern frequency 1kHz is 1ms per sample.
   
   
   An osciloscope picture of a correct measurement is shown here:
   
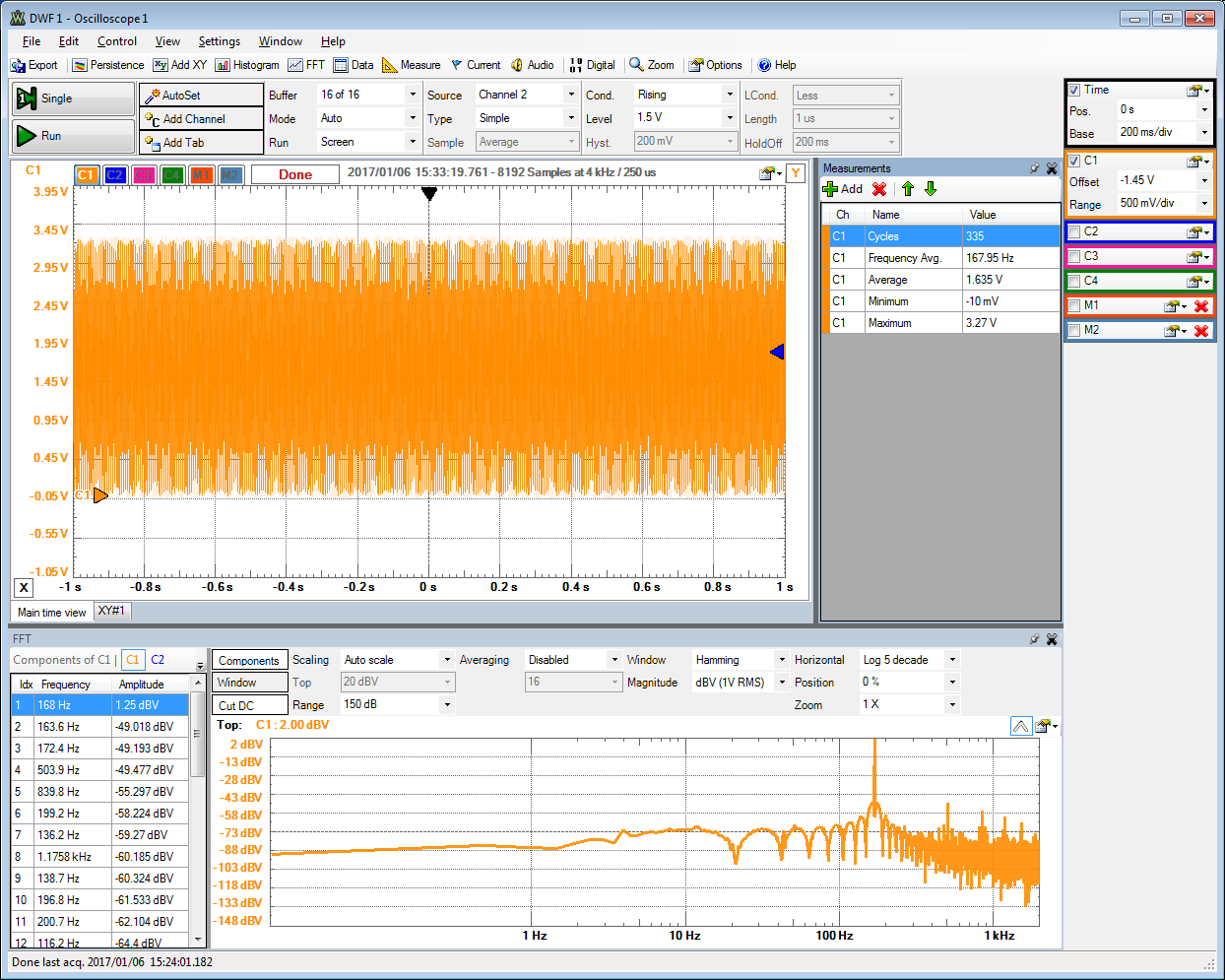
   The FFT window allows to show the 'Components', the magnitude of biggest frequency components. It can show the 'Window' to suppress bleeding and can 'Cut DC'.
   
   Every 250us a sample is generated by the pattern generator and taken by the oscilloscope.
   There is no bleeding visible. The signal has an amplitude of 1.25dBV.
   The first harmonic has -49.018 dBV.
   Unfortunately the total noise level is not calculated.
   Therefore the time data are exported ('Main Window' Copy to clipboard) and converted to positive integer numbers round(16k * Vout) + 135 and filled into the web page:
   FFT Javascript
   After 'Read integer data' and 'Generate Charts' the following graphs and numbers are available:
   
   

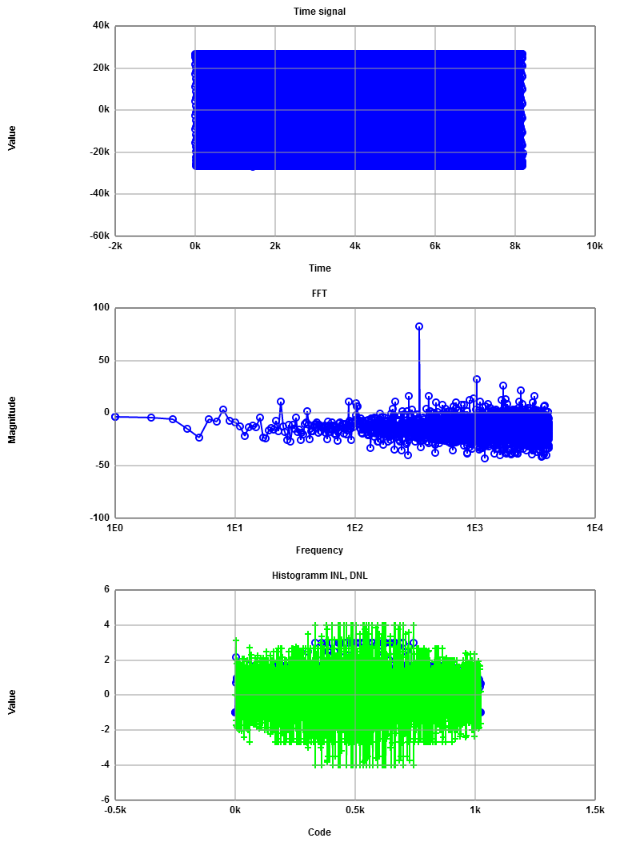
   Signal to Noise

   Frequency	signal magnitude dB	Total noise magnitude dB
   344	82.53	34.51
   1032	31.84	31.14
   1720	26.05	29.53
   2408	21.14	28.84
   280	16.48	28.58
   3096	16.39	28.31
   408	16.37	28.03
   968	13.63	27.87
   1784	13.45	27.71
   904	12.72	27.57
   1656	12.46	27.43

   
   The signal to noise ratio is 82.53 dB - 34.51 dB = 48 dB. This is 48 dB / 6.07 dB = 8 Bit.
   Removing the next 3 harmonics would reduce the noise level to 28.84 dB giving nearly one Bit more.
   The INL, DNL charts show variations of up to 4 LSBs for a 10 Bit ADC bringing ENOB down to 8 Bit.
   It is possible at the web page to reduce the number of Bits to 7 (rounding) giving an INL and DNL below 0.5.
   
   
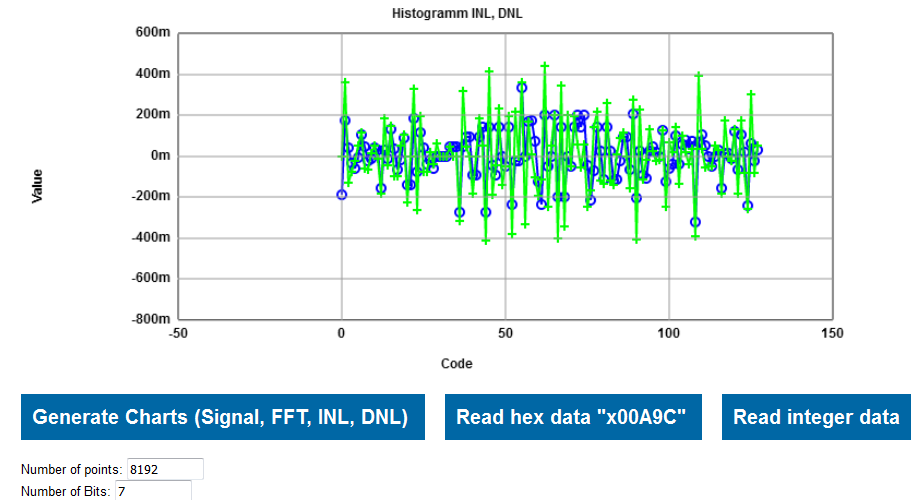
   Investigation of a 1kHz pattern generator signal shows the following FFT.
   Each value of the pattern generator is sampled 4 times by the oscilloscope.
   
   

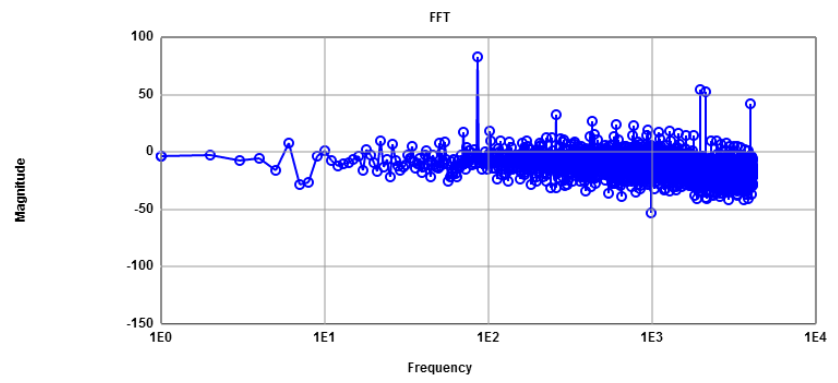
   Signal to Noise

   Frequency	signal magnitude dB	Total noise magnitude dB
   86	82.57	56.52
   1962	53.82	53.18
   2134	52.75	42.97
   4010	42.02	35.92
   258	32.12	33.58
   430	26.95	32.51
   602	24.19	31.82
   774	22.53	31.28
   946	19.1	31.01
   102	17.93	30.79
   1274	17.8	30.56

   The signal to noise ratio is reduced to 82.57 dB - 56.52 dB = 26 dB. Due to the 3 harmonics at high frequencies, due to the incorrect (to many samples) oscilloscope sampling.
   
   
   
8. Document your results.
   
   

   Solution and Outlook

   
   
   This laboratory showed challenges measuring DACs, while proving to be able to build a 8 Bit DAC.
   The first real experience was to determine necessary accuracy for minimum, maximum and step size.
   The second real experience was the effort to measure all codes of an DAC.
   The third real experience lay in the FTT analysis to determine the right number of samples, sampling time and pattern generator frequency and synchronization. Calculating a correct noise level was also very dificult.
   
   It is planned to use a band-stop filter to suppress the original signal and to be able to get a good estimate of the noise level.
   In the next laboratory a sigma delta modulator is built and used to measure accuracy, INL, DNL and signal to noise ratio.
   It is then difficult to determine whether errors are coming fromn the DAC or ADC.

Report

Grading: