Microelectronics Laboratory

2024 CMOS Performance

Prof. Dr. Jörg Vollrath

Outline

Motivation
Technology, transistor parameters and circuit performance
SPICE Transistor Models
International Electronic Device Meeting IEDM
Technology presentations, IV curves, transistor parameter tables
Feature size: 180 nm, 130 nm, 90 nm, 65 nm, 40 nm/45 nm, 32 nm, 22 nm, 14 nm, 10 nm ..
Circuits
Inverter, inverter chain and ring oscillator
Transistor parameters and circuit performance
Optimum performance point:
What is optimum performance?
How to compare technologies?
Transistor: W, L, WN/WP ratio
Operating point: VDD+-10%, T (-10°C, 22°C, 90°C)
Deliverables

This laboratory looks at technology scaling, transistor and circuit performance.

A step by step update will be done.

Motivation

With technology scaling transistor and circuit performance is changing
There are limited examples of SPICE model files available
Searching for SPICE model 40 nm / 90 nm / 130 nm
There are limited performance examples for simulation and measurement of transistors and circuits
Rarely transistor curves and parameters are shown with typical ring oscillator and inverter measurements
Goal

Find transistor IV curves and parameters
Do circuit measurement and simulations
Look at relationship between technology node and circuit performance

Technology nodes: Wikipedia technologie nodes (02 History Microelectronics)
MOSFET models: 03 MOSFET, Microelectronics

SPICE transistor models

Select one SPICE simulation technology file
Search on the internet for SPICE models
List search terms and possible results
Can you find more SPICE models than available in this class?

MOSFET models: 03 MOSFET, Microelectronics

International Electronic Device Meeting IEDM

IEDM is the flagship meeting concerning device development
Search at ieeeexplore for conference publications refering to device performance
Select one publication for a technology node:
- with transistor IV curves
- transistor parameter table (F, V_th, β, λ, W, L, C_ox) and
- possible performance data (V_DDmax, I_on, I_off, f_t, gain, R_DSon).

Performance Circuit: Inverter and Ring Oscillator

Inverter
Inverter chain
Ring oscillator

Library: Lab05_2024.jelib

Link: Lab05_2024.jelib

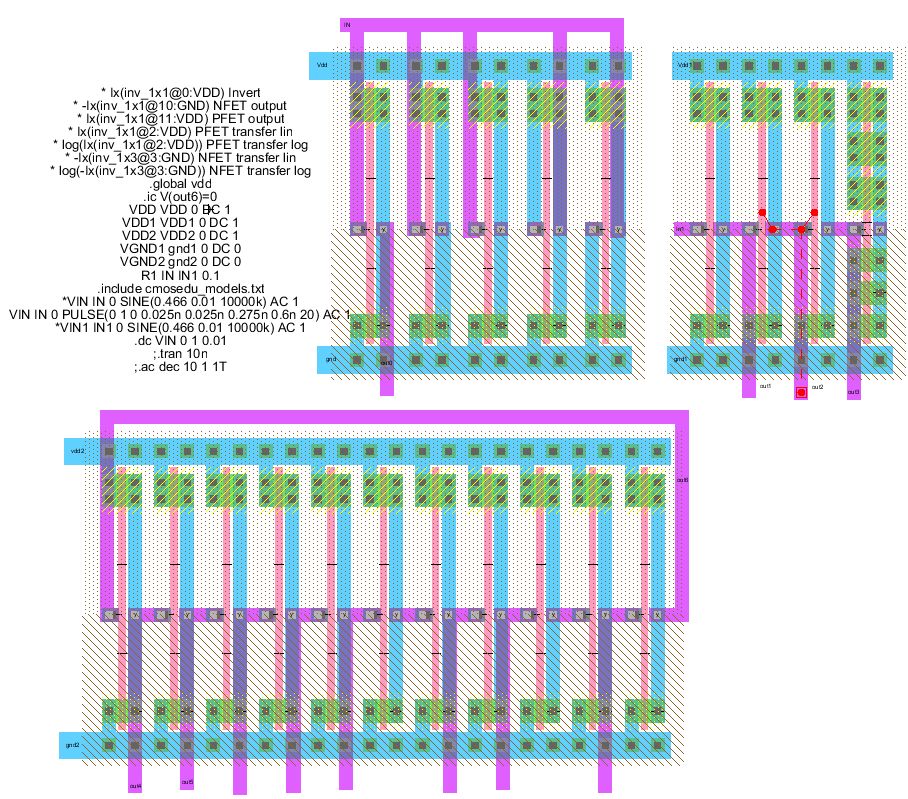
Cell: 'Performance' for .AC and .TRAN ring oscillator and delay simulation
Cell: 'PerformanceDC' for .DC simulation

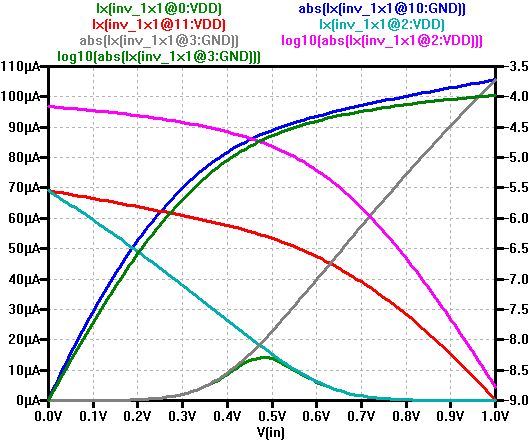
Static IV output curves with an Inverter
VDDmax, IDSN, IDSP, λ
Inverter chain
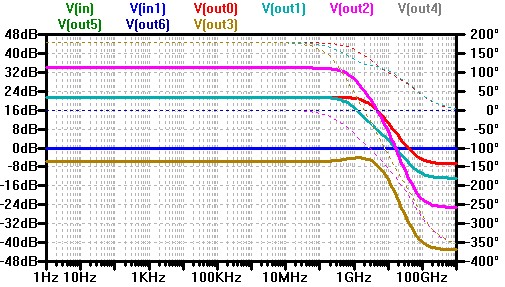
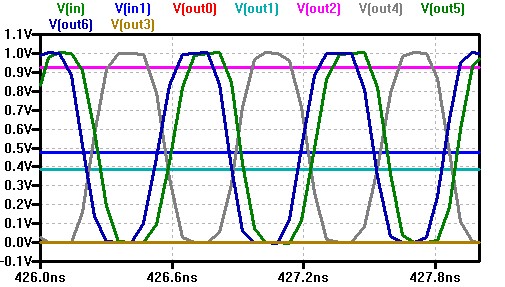
Ring oscillator
Variation of number of unit transistor: mN, mP, sN, sP
m number of transistors in parallel (LTSPICE parameter)
s number of transistors in series
Simulate the circuits, extract parameters and modify WN, WP for optimum performance

Transistor parameters: V_thn, β (KP,KN), λ
Electrical parameters: V_DDmax, (I_DSmax), I_off, R_on, C_ox
Performance parameters: t_delay, f_CLKmax, gain, f_t

Most of the time MOSFETs are not available for measurement, therefore an inverter is used.
The input is fixed at VDD or gnd. With a load NFET or PFET current is measured for the output curve.
The inverter Vout, Iout versus Vin curve gives the threshold voltage V_thn, V_thp and the β (KP, KN).

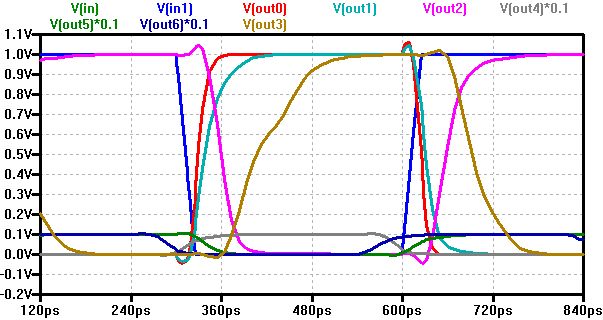
An Inverter chain gives the propagation delay per stage.
t = 0.7 * R * C
The average power consumption for full charging should be:
Pavg = V * I = V * C * V * f
Changing the load 1,2,3 inverters, changes C while keeping R constant.

DC Simulation Inverter (50nm)

* Ix(inv_1x1@0:VDD) Invert
* -Ix(inv_1x1@10:GND) NFET output
* Ix(inv_1x1@11:VDD) PFET output
* Ix(inv_1x1@2:VDD) PFET transfer lin
* log10(abs(Ix(inv_1x1@2:VDD))) PFET transfer log10
* -Ix(inv_1x1@3:GND) NFET transfer lin
* log10(abs(Ix(inv_1x1@3:GND))) NFET transfer log10
.option TEMP = 27
VIN IN 0 SINE(0.466 0.01 10000k) AC 1

.dc VIN 0 1 0.01

Vth, β λ; Imax, Ioff

Trace:
Ix(inv_1x1@0:VDD) -Ix(inv_1x1@10:GND) Ix(inv_1x1@11:VDD) Ix(inv_1x1@2:VDD) log10(Ix(inv_1x1@2:VDD)) -Ix(inv_1x3@3:GND) log10(-Ix(inv_1x3@3:GND)) NFET transfer log
λ is valid for the linear part of the output curve IDS(VDS) where VGS-Vth < VDS
One point is maximum VDD, IDS and the other is less VDS where IDS(VDS) is still linear.
λ = (IDS1 - IDS2)/(IDS2 * UDS1 - IDS1 * UDS2)
NFET: λn = (105uA-100uA) /(100uA * 1V - 105uA * 0.8V) = 5uA/(16uaV) = 0.3 V-1
PFET: λp = (69uA-61uA) /(69uA * 1V - 61uA * 0.7V) = 8uA/(27uaV) = 0.3 V-1

KNn = 2 * IDSmax * L / W / (1+ λ VDS) / (VGS -Vth)^2
NFET: KNn = 2 * 105 uA / 3.5 / (1+ 0.3) / (1 V - 0.25)^2 = 82 uAV^-2
PFET: KNn = 2 * 69 uA / 5 / (1+ 0.3) / (1 V - 0.25)^2 = 38 uAV^-2

RDS = W/L * (VDD-V(IDSmax/2))/(IDSmax - IDSmax/2)
RDSn = 3.5 * 0.35 V / 51 uA = 20 kΩ
RDSp = 5 * 0.35V / 35 uA = 50 kΩ

Gain:
Look at I_DS at voltage VDD/2 for gain calculation.
\( v_u = \frac{dVout}{dVin} = \frac{1}{ I_{DS}(V_{DD}/2) \cdot λ \cdot RDS} \)
\( R_{DS} = \frac{1}{\frac{1}{R_{DSn}} + \frac{1}{R_{DSp}}} = 14 k\Omega \)
\( v_u = \frac{1}{15 uA \cdot 0.3 V^{-1} \cdot 14 k\Omega} = 24 \)
a_vu = 21 dB
Are there better equations for simple calculation of parameters?
What would be the optimum WN/WP ratio?
What is the effect of changing L?
What happens if LN/LP is not 1?

AC Simulation Inverter (50nm)

VIN IN 0 SINE(0.466 0.01 10000k) AC 1
.ac dec 10 1 1T

V(out0): output inverter, no load
ft 40GHz, a = 22dB
V(out1): load inverter
ft 16.8 GHz, a = 22 dB

A operation point of 0.466 V is set to be at the maximum gain point of the inverter.

Definition of transit frequency ft(a = 0 dB)
ft = gm/2/pi/CGD = 1/RDS/2/pi/CGD
Estimation of Area for CGD:
W * L no load = 8.5; W * L inverter load = 2.5 * 8.5 = 21
Cox = 8.5 CGD
Cox = 1/(W * L * ft * RDS * 2 * pi) = 1/(8.5 * 40 GHz * 14 kΩ * 2 * 3.14) = 33 aF

How is a and ft changing with temperature?
How is a and ft changing with voltage (Offset/bias and VDD)?

.step TEMP LIST -10 27 90
.step VDD1 0.9 1.1 0.1

Delay Simulation Inverter and Ring Oscillator (50nm)

Ring oscillator:
Cycle time 650 ps
11 stages (60ps per stage)

VIN IN 0 PULSE(0 1 0 0.025n 0.025n 0.275n 0.6n 20) AC 1
.tran 10n

Delay:
Nominal 1x: 2.5 Cox HL: 22 ps, LH: 28 ps;
Load 3x: 5.5 Cox 32ps, 46 ps

Delay is measured from V(out1) to V(out2) (no load) and from V(out2) to V(out3) (with load) for rising and falling edges.

Performance Table

Name	Nominal			Change	Change F
Feature size	50 nm (Baker)	VDD max	1 V
T	27 °C	ImaxInv	15 uA
Ln	50 nm	Lp	50 nm
Wn	175 nm	Wp	250 nm
IDSn max	105 uA	IDSp max	70 uA
Vthn	0.25 V	Vthp	-0.25 V
KNn	82uAV-2	KNp	38uAV-2
λn	0.3 V-1	λp	0.3 V-1
Ioffn	1E-9 A	Ioffp	2E-9 A
Coxn	33 aF	Coxp	33 aF
RDSn	20 kΩ	RDSp	50 kΩ
gain	22 dB, 100	tRing11	650 ps
ftmax	40 GHz	ftreal	16 GHz
tpdHLx1	22 ps	tpdLHx1	28 ps
tpdHLx3	32 ps	tpdLHx3	46 ps

Column Change can be:

±10% change in L, W, VDD
T -10C, 90C (.option TEMP = 27)
Optimized NFET, PFET dimension

Deliverables

Email: Your paper search technology node and LTSPICE technology node
Discussion of LTSPICE model search (1)
One cited IEDM paper PFET, NFET IV curves and performance parameter table (1)
LTSPICE simulation results comparing 50nm results to another technology (2)
Change transistor model .include file, change VDD and layout technology scaling factor (VLSI Electric), ( Change NFET, PFET transistor width in layout)
LTSPICE simulation comparing temperature or/and voltage variations (1)
Discussion of optimum transistor length and width and optimum performance point (1)
Total 6/7 laboratories left: 2 page report, due date: 08.07.2024
Submit a pdf file via email.
Pdf file name: 2024_Lab05_<LastName><FirstName>.pdf

Future work and questions

Are NFET, PFET roll-off curves matched and optimized for L?
Investigate frequency, power consumption and number of inverters in ring oscillator.
Optimize AC and ring oscillator graphs
Show parameters Vth, Imax, λ, Imax, Ioff in DC graph.
What accuracy is needed?
Is consistency more important than accuracy?
Dependence of Ion/Ioff ratio on W and L (# of transistor in parallel and series)

2024 CMOS Performance Microelectronics Prof. Dr. Joerg Vollrath