Elektronik04 FrequenzgangProf. Dr. Jörg Vollrath03 Konfigurationen |

|
Video der 4. Vorlesung 24.3.2021
|
Länge: 1:18:46 |
0:2:22 ro und gm 0:6:17 vu = - 2961 mit VT = 25 mV, vu = -2870 (VT = 25.8 mV) 0:10:22 Näherungsweise Rechnung 0:12:40 Aufgabenstellung mit REsig 0:15:27 Diskussion Funktion von RE 0:19:57 AC Frequenzgang 0:24:57 Verstärkung von -141 bestätigt mit LTSPICE 0:27:41 Simulation des Kleinsignalersatzschaltbildes 0:33:11 Spannungsteiler Rsig, Rin 0.89 0:35:17 Variationen durch Bauelemente Streuung 0:36:37 Einfluss der Kapazitäten 0:39:27 Eingangshochpass 0:44:57 20 dB, 40 dB pro Dekade 0:47:19 Praktikum: Simulation, Aufbau Common Emitter 0:50:14 Hochfrequenzmodell des BJT 0:53:37 Ersatzschaltbild Miller Kapazität 0:59:50 Yi = (1 + vu) Y1 = (1 + gm ro) Y1 1:5:27 Klirrfaktor, Linearität 1:10:27 Formel Erläuterung 1:13:17 Signal und Harmonische |
Übersicht
- Fortführung Beispiel:
RE und die Parallelkapazität - Hausaufgabe: Rechnung mit RE 50 Ohm in Reihe
- Simulation Kleinsignalersatzschaltbild
- Praktikum
- Frequenzgang
- Millerkapazität
Aufgabenstellung mit REAC = 50 Ω
Aufgabenstellung
Erstellen Sie das Kleinsignalersatzschaltbild der dargestellten Schaltung mit kurzgeschlossenen Kapazitäten, ohne Spannungsteiler R1, R2, aber mit REAC.Der Widerstand RE wird aufgeteilt in REAC = 50 Ω und Re = 550 Ω
Berechnen Sie die Spannungsverstärkung uv1 ohne Berücksichtigung von RC und RL.
Berechnen Sie die Spannungsverstärkung uv1 mit Berücksichtigung von den Widerständen RC und RL: R = 1 / (1/RC + 1/RL).
Startpunkt
T=300K, VT =25.85 mV, β = 179, IS= 14.34 fA, VA=74.03,VCC = 12V, ie = 5mA, RL = 100kΩ, Risg = 100 Ω
C=10uF
VRE = VCC/4, VRE = VCC/3, IR2 = 10 · IB
Ausgangspunkt ist der Arbeitspunkt der Schaltung aus der vorigen Vorlesung.
R1 = 27 kΩ, R2 = 13.3 kΩ, RC = 800 Ω, RE = 800 Ω
Ri = 825 Ω, ro = 15.8 kΩ (14.8 kΩ);, Rout = 756 Ω
Spannungsverstärkungen nur des Transistors vu1, mit RC und RL vu2:
vu1 = -2869, vu2 = -141
Die externe Beschaltung verringert die Spannungsverstärkung.
Eingangsspannungsteiler
Am Eingang liegt noch der Spannungsteiler von Rsig und R1, R2, ri, der die Gesamtverstärkung der Schaltung verringert.vx = 0.89
Achten Sie auf das Verhältnis von Quellenwiderstand und Eingangswiderstand.
Frequenzverhalten AC Simulation
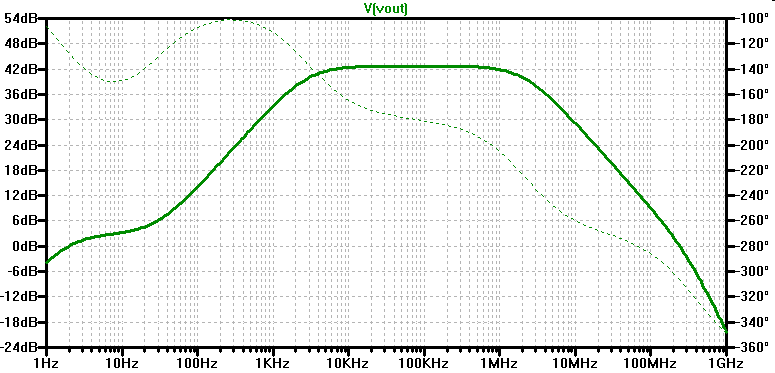
Man sieht mehrere Pole und Nullstellen.
Unterhalb von 1 Hz sitzt der Hochpass bzgl. CC2.
Bei ca. 2 Hz sitzt der Hochpass bzgl. CC1.
Zwischen 2 Hz und 30 Hz begrenzt RE die Verstärkung, bevor dann Ce RE kurzschliesst.
Die oberen Eckfrequenzen bei 1 MHz und 400 MHz werden durch die Transistorkapazitäten CJC und CJE erzeugt (nächste Folie).
Beispielhaft wird die Übertragungsfunktion für CC1 gebildet:
\( \frac{\underline{U_{B1}}}{\underline{U_{sig}}} = \frac{RI1}{Rsig + \frac{1}{j ω CC1 } + RI1} \)
Bei der Berechnung des Eingangswiderstands ri kann RE wirksam sein.
\( RI1 = \frac{1}{\frac{1}{R1} + \frac{1}{R2} + \frac{1}{ri}} \)
\( \frac{\underline{U_{B1}}}{\underline{U_{sig}}} = \frac{j ω C_{C1} RI1 }{1 + j ω C_{C1} (R_{sig} + RI1) } \)
\( f_{3dB1} = \frac{\omega}{2 \pi} = \frac{1}{2 \pi C_{C1} (R_{sig} + RI1)} \)
U2-24: Sedra (7th), Fig 10.8
Warum wird für CC1 RE nicht berücksichtigt?
Warum ist τCE die kürzeste Zeitkonstante?
Kann man das nicht mit CE korrigieren?
Im Beispiel benötigt man dazu mehr als 1 mF Kapazität.
Unterhalb von 1 Hz sitzt der Hochpass bzgl. CC2.
Bei ca. 2 Hz sitzt der Hochpass bzgl. CC1.
Zwischen 2 Hz und 30 Hz begrenzt RE die Verstärkung, bevor dann Ce RE kurzschliesst.
Die oberen Eckfrequenzen bei 1 MHz und 400 MHz werden durch die Transistorkapazitäten CJC und CJE erzeugt (nächste Folie).
Beispielhaft wird die Übertragungsfunktion für CC1 gebildet:
\( \frac{\underline{U_{B1}}}{\underline{U_{sig}}} = \frac{RI1}{Rsig + \frac{1}{j ω CC1 } + RI1} \)
Bei der Berechnung des Eingangswiderstands ri kann RE wirksam sein.
\( RI1 = \frac{1}{\frac{1}{R1} + \frac{1}{R2} + \frac{1}{ri}} \)
\( \frac{\underline{U_{B1}}}{\underline{U_{sig}}} = \frac{j ω C_{C1} RI1 }{1 + j ω C_{C1} (R_{sig} + RI1) } \)
\( f_{3dB1} = \frac{\omega}{2 \pi} = \frac{1}{2 \pi C_{C1} (R_{sig} + RI1)} \)
U2-24: Sedra (7th), Fig 10.8
Warum wird für CC1 RE nicht berücksichtigt?
Warum ist τCE die kürzeste Zeitkonstante?
Kann man das nicht mit CE korrigieren?
Im Beispiel benötigt man dazu mehr als 1 mF Kapazität.
Frequenzeigenschaften und Millerkapazität
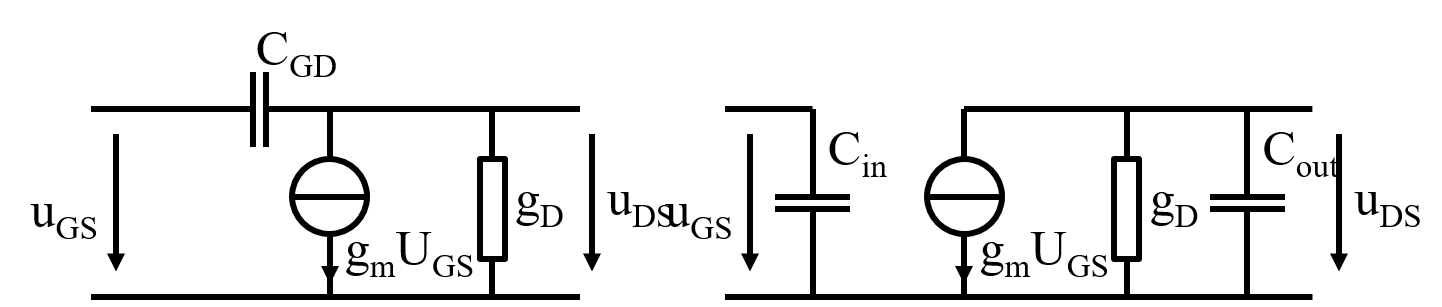
\( j \omega C_{in} = \frac{\underline{I}_{in}}{\underline{U}_{in}} = \frac{\left( \underline{U}_{in} + \frac{g_m \underline{U}_{in}}{g_D}\right) j \omega C_{GD}}{\underline{U}_{in}} \)
\( C_{in} = \left( 1 + \frac{g_m}{g_D} \right) C_{GD} = \left( 1 + |v_{u}| \right) C_{GD} \)
\( C_{out} = C_{GD} \)
Hier wird ein MOSFET Kleinsignalersatzschaltbild gezeigt.
Für eine einfacherer Betrachtung möchte man die Kapazität CGD zwischen Eingang und Ausgang
durch eine äquivalente Eingangskapazität Cin und
Ausgangskapazität Cout ersetzen.
Die äquivalente Kapazität \( C_{in} \) ist viel größer als \( C_{GD} \).
Die Betrachtung gilt auch für einen beliebigen komplexen Widerstand.
Die äquivalente Kapazität \( C_{in} \) ist viel größer als \( C_{GD} \).
Die Betrachtung gilt auch für einen beliebigen komplexen Widerstand.
Millereffekt
Diese Kapazität begrenzt die maximale Frequenz bei der noch eine Verstärkung erzielt werden kann. 15 Elektronik 3 VerstärkerKlirrfaktor
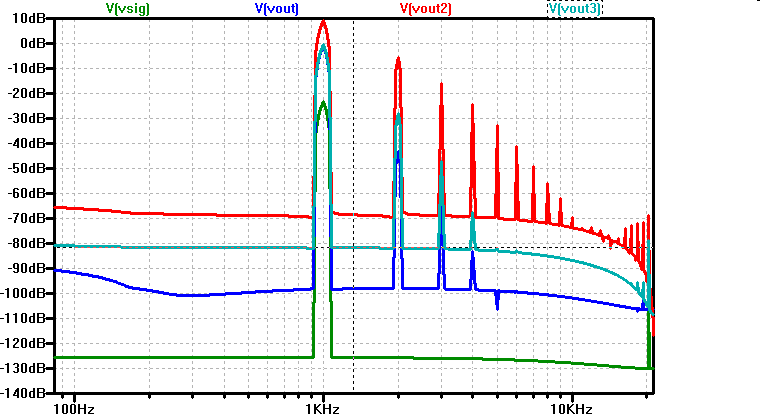
V(sig): Signal
LTSPICE FFT 512 Punkte.
| Schaltung | Signal in | Signal in | Signal out | Signal out | 1.Harmonische | Klirrfaktor k1 |
| CE V(Vout2) | 0.1 V | -23 dB | 3.3 V | 10 dB | - 5 dB | -15 dB, 0.18 |
| CE kleines Signal V(Vout3) | 0.03 V | -33 dB | 1 V | 0 dB | - 28 dB | -28 dB, 0.04 |
| CE + RE V(Vout) | 0.1 V | -23 dB | 1V | 0 dB | - 44 dB | -44 dB, 0.006 |
Kommen die Verzerrungen, der Klirrfaktor durch die grosse Amplitude?
Je kleiner die Amplitude am Eingang desto linearer ist der Verstärker.
Die erste harmonische Oberwelle ist kleiner.
Kann der Widerstand RE die Verzerrungen, den Klirrfaktor verkleinern? Mit dem Widerstand RE wird die erste harmonische Oberwelle noch kleiner.
Die erste harmonische Oberwelle ist kleiner.
Kann der Widerstand RE die Verzerrungen, den Klirrfaktor verkleinern? Mit dem Widerstand RE wird die erste harmonische Oberwelle noch kleiner.
Klirrfaktor
\( k = \sqrt{\frac{V_1^2 + V_2^2 + ...}{V_0^2 + V_1^2 + V_1^2 + ..}} \)
Wertebereich von 0..1
V0: Signalamplitude
Vi: Amplituden der Harmonischen
LTSPICE Simulation der Schaltung
Eingangsamplitude: 0.1 V, 30mV
Ausgangsamplitude
FFT in LTSPICE
Diskussion AC Simulation und transiente Simulation
U2: 29-31
Wie kann man den Klirrfaktor in dB umrechnen?
Beispiel mit einer harmonischen und 40 dB Unterschied zwischen Signal und erster harmonischen:
\( k1 = \sqrt{\frac{V_1^2}{V_0^2 + V_1^2}} \)
Für kleine Klirrfaktoren:
\( k1 = \sqrt{\frac{V_1^2}{V_0^2}} = \frac{V_1}{V_0} \)
\( 20 log(k1) dB = 20 log(V_1) - 20 log(V_0) \)
40 dB entsprechen dem Faktor 100.
V0 = 1 V, V1 = 0.01 V
k1 = 0.01
k1 = -40 dB
Auflösung in Bits:
1 V / 128 = 0.0078125 V
128 = 27 entspricht 7 Bit.
Ein Klirrfaktor von 1% (1/1000) entspricht dann einer Auflösung von 10 Bit 210 = 1024 unnd 20 log(1000) = 60 dB.
Eingangsamplitude: 0.1 V, 30mV
Ausgangsamplitude
FFT in LTSPICE
Diskussion AC Simulation und transiente Simulation
U2: 29-31
Wie kann man den Klirrfaktor in dB umrechnen?
Beispiel mit einer harmonischen und 40 dB Unterschied zwischen Signal und erster harmonischen:
\( k1 = \sqrt{\frac{V_1^2}{V_0^2 + V_1^2}} \)
Für kleine Klirrfaktoren:
\( k1 = \sqrt{\frac{V_1^2}{V_0^2}} = \frac{V_1}{V_0} \)
\( 20 log(k1) dB = 20 log(V_1) - 20 log(V_0) \)
40 dB entsprechen dem Faktor 100.
V0 = 1 V, V1 = 0.01 V
k1 = 0.01
k1 = -40 dB
Auflösung in Bits:
1 V / 128 = 0.0078125 V
128 = 27 entspricht 7 Bit.
Ein Klirrfaktor von 1% (1/1000) entspricht dann einer Auflösung von 10 Bit 210 = 1024 unnd 20 log(1000) = 60 dB.
Nächste Vorlesung
- Emitterwiderstand
- Optimierung der Schaltung
- Obere 3db Eckfrequenzen
- MOSFET common gate, drain
- Kaskode
05 CE Analyse