Elektronik

10 Komplexe Rechnung

Prof. Dr. Jörg Vollrath

03 Berechnung

Video der 15. Vorlesung 24.11.2020

Länge: 01:28:01

0:0:0 Willlkommen

0:0:21 QR code

0:2:19 Komplexe Rechnung

0:5:1 Audioverstärker

0:9:14 Blockdiagramm

0:10:15 Messung mit R, L, C

0:13:19 Waveforms

0:13:49 Signalgenerator: Frequenz, Amplitude

0:15:43 Frequenz und Periodendauer, Ergebnissicherung

0:18:8 Oszilloskop

0:19:13 Der Trigger Source, Condition, Level

0:21:3 x-Achse, Zeit, Time, Base

0:22:13 Messung

0:23:29 y-Achse, Range, zu klein, zu gross, abschneiden

0:24:58 Stromberechnung M3 =( U1 -U2)/100 Ohm

0:28:18 Signal der Kapazität auf dem Oszilloskop

0:29:48 Phasenverschiebung

0:31:38 Zeigerdarstellung

0:32:56 ω Kreisfrequenz

0:34:13 Komplexe Zahlen

0:38:1 R-Form und P-Form

0:40:39 Rechnung Differentialgleichung, Komplexe Funktion

0:42:3 Ohmsches Gesetz im komplexen

0:44:13 Komplexe Operationen Multiplikation

0:47:43 Oszilloskopbild 20 kHz der Kapazität 90° Phasenunterschie

0:49:29 50 kHz Frequenz

0:50:35 10 kHz Frequenz

0:53:3 Komplexe Widerstände I = j W C U

0:53:48 Messung der Induktivität

0:56:43 U = j w L I

0:59:56 Differentialgleichung L

1:1:57 Vergleich mit Oszilloskopbild

1:4:42 Differentialgleichung C

1:5:12 Komplexer Widerstand Internetseite

1:6:33 Lösungsanzeige

1:8:21 Modifikation der Bauelemente

1:11:8 Rechnen Sie 4 komplexe Widerstände aus

1:15:42 Methode zum Zusammenfassen von Widerständen

1:17:47 Z = R + jX

1:19:42 Y = G + jB = 1/Z

1:21:26 Ansatz nochmals überprüfen

1:22:32 Weitere Umformung

1:24:47 Konjugiert komplex erweitern

1:26:59 Betrag

Übersicht

Audioverstärker

Sinusförmige Wechselspannungen
Komplexe Zahlen und Rechnung

Zeiger: R-Form, P-Form
Realteil, Imaginärteil, Betrag, Phase
Addition, Multiplikation, konjugiert Komplex erweitern

Widerstand, Kapazität, Induktivität
Kapazität

Differentialgleichung
Komplexer Widerstand

Induktivität

Differentialgleichung
Komplexer Widerstand

Zusammenschaltung komplexer Widerstände
Übertragungsfunktion

Projekt 2. Semester Audioverstärker

Wechselspannung: Audiosignal, Wechselspannungsquelle
Komplexe Darstellung
Filter: Tiefpass, Hochpass, Bandpass: R, L, C Bauelemente und Schaltungen
Komplexe Übertragungsfunktion, Bodediagramm, Maß dB
Verstärker und aktive Filter: Operationsverstärker mit R, L, C, MOSFET

Wo stehen Sie bei der Betrachtung von Wechselspannungsnetzwerken?

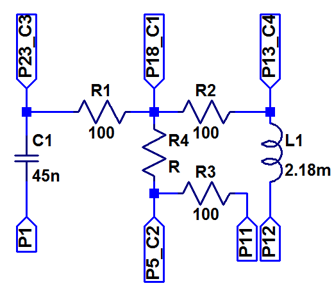
Messung mit R, L und C bei 20 kHz

R = 100 Ω
C1 = 45 nF
L1 = 2.18 mH, 20 Ω

Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Jede reale Spule hat einen ohmschen Widerstand und eine Induktivität.

Fragen:

Was ist eine Oszilloskop?
Was beobachten Sie?
Welche Kenngrößen einer Sinusschwingung gibt es?
Was passiert, wenn man diese verändert?

Die Schaltung wird mit dem Electronic Explorer Board verbunden.
P18 AWG1, OSC1; P1,P11,P12, GND; P5 OSC2 (R), P23 OSC3 C, P13 OSC4 (L)
Berechnung der Ströme:
IR: M1 = (C1 -C4) / 100
IC: M2 = (C1-C3)/100
IL: M3 = (C1-C2)/100

Oszilloskop

In einem festen Zeitraster werden Spannungen mit einem Analog-Digital-Wandler erfasst.
Das Zeitraster (Time, Base), x-Achse und die Spannungsauflösung (Range), y-Achse kann man einstellen.
Mit der Position und dem Offset kann man die Darstellung nach rechts oder links bzw. oben oder unten verschieben.
Ein Trigger (Source, Condition, Level) sorgt für ein stehendes Bild.

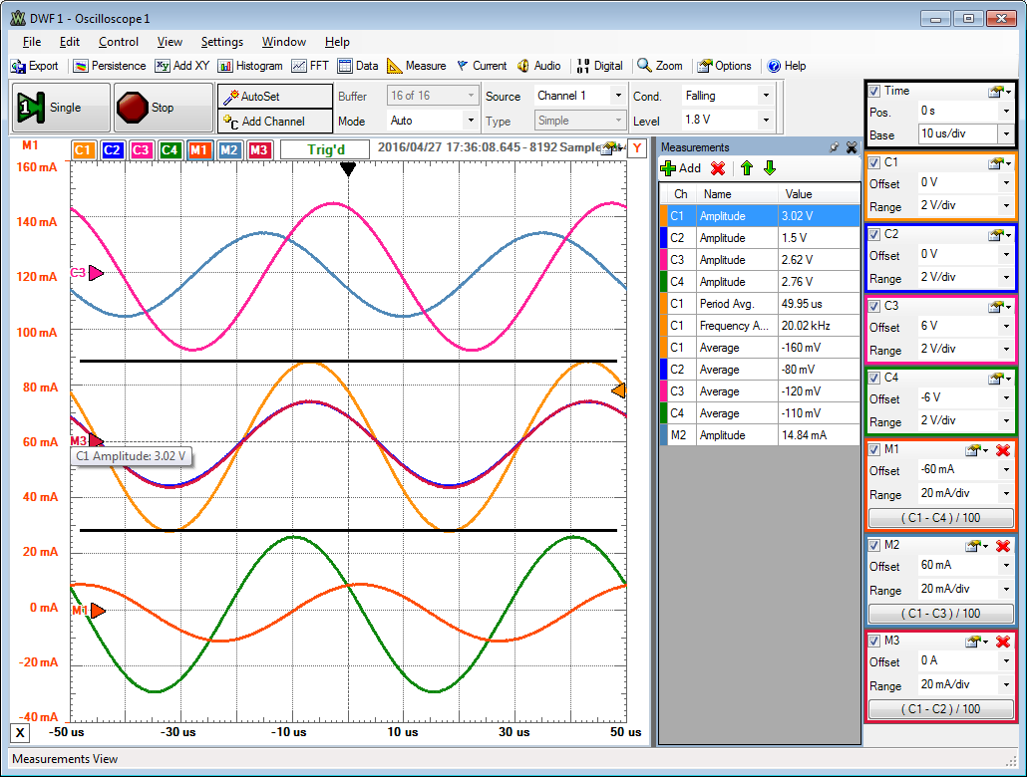
Messung

Kapazität

	f	20 kHz	50 kHz	10 kHz
C3	U	2.6 V	1.74 V	2.9 V
M2	I	15 mA	24.6 mA	8.3 mA

Je höher die Frequenz, desto kleiner der Widerstand.

$\frac{U}{I} = \frac{1}{\omega C}$

$\frac{\underline{U}}{\underline{I}} = \frac{1}{j \omega C} = \underline{Z}_C$

Induktivität

	f	20 kHz	50 kHz	10 kHz
C4	U	2.72 V	2.95 V	2.2 V
M1	I	10.54 mA	4.79 mA	17.48 mA

Je höher die Frequenz, desto größer der Widerstand.

$\frac{\underline{U}}{\underline{I}} = j \omega L = \underline{Z}_L$

Zeigerdarstellung

Eine Sinusfunktion wird mit einer komplexen Zahl dargestellt.
Die komplexe Zahl enthält Betrag und Phasenwinkel zum Zeitpunkt t = 0 s.

Komplexe Zahlen und Rechnung

Mathematische Beschreibung von Zeigern: komplexe Zahlen

U = a + j b mit

$j = \sqrt{-1}$
Bezugsachse ist die reelle Achse

Zeitpunkt t = 0

Realteil: û cos φ_u
Imaginärteil: û sin φ_u

û: Amplitude

Spannung in der komplexen Ebene.
u(t) = û cos(ω t + φ_u) + j û sin(ω t + φ_u)
Eulersche Gleichung

$e^{j \phi} = cos \phi + j sin\phi$

Komplexe Spannung und komplexer Strom

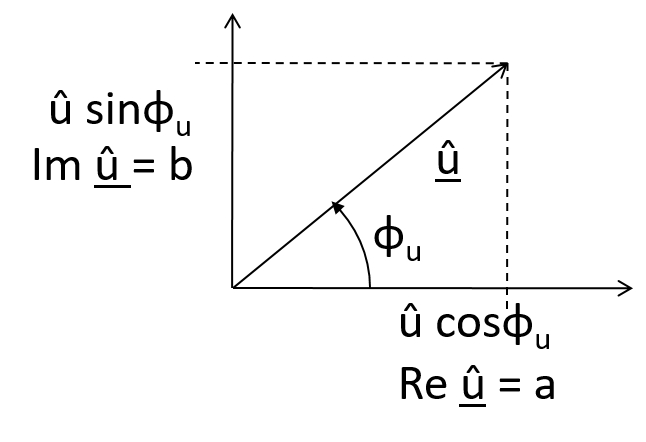
In der Elektrotechnik wird mit j statt i gerechnet.
Quelle: GET2_04_17

R-Form und P-Form

R-Form	P-Form
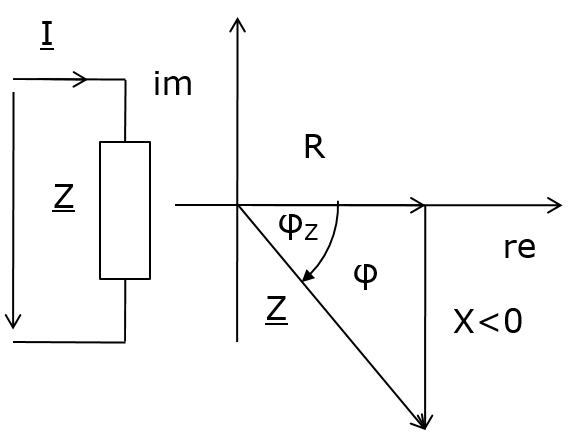
$\underline{Z} = R + j X$ $R = Z cos\phi$ $X = Z sin\phi$ Addition von Spannungen und Strömen Reihenschaltung von Widerständen $\underline{Z} = R + j X = \underline{Z}_1 + \underline{Z}_2$ $\underline{Z} = (R_1 + R_2) + j (X_1 + X_2)$	$\underline{Z} = Z \underline{/\phi} = Z \cdot e^{j\phi}$ $Z = \sqrt{R^{2} + X^{2}}$ $\phi = arctan{\frac{X}{R}}$ Multiplikation, Division Umwandlung Widerstand und Leitwert

Rechnung für Sinusförmige Wechselgrößen

Überlagerung sinusförmiger Wechselgrößen

Differentialgleichung

Im Zeitbereich
Mit Hilfe von komplexen Zeitfunktionen

Berechnung im komplexen

Zeigerdiagramm mit komplexen Effektivwerten (grafisches Verfahren)
Algebraische Gleichung in komplexen Effektivwerten (Symbolische Methode)

Ohmsches Gesetz im Komplexen

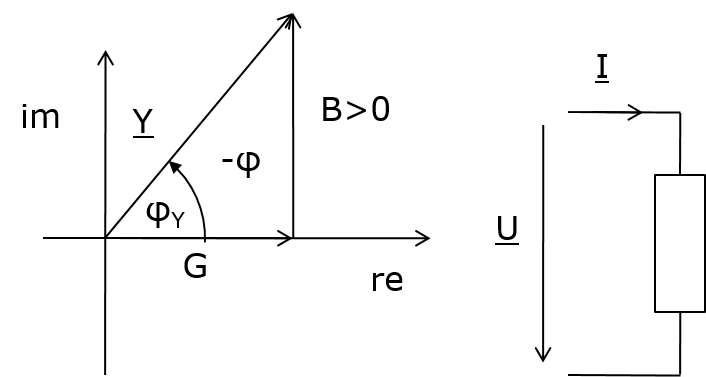
Bisher:

$U = I \cdot R = \frac{I}{G}$
R: Widerstand, G: Leitwert

Komplex:

$\underline{U} = \underline{I} \cdot \underline{Z} = \frac{\underline{I}}{\underline{Y}}$

Komplexer Widerstand in R- und P-Form:

$\underline{Z} = R + j X = Z \underline{/\phi}$

Realteil R : Wirkwiderstand, Resistanz (resistance)
Imaginärteil X: Blindwiderstand, Reaktanz (reactance)

$\underline{/\phi}$ : man spricht Versor φ, Winkel φ

Komplexer Leitwert in R- und P-Form:

$\underline{Y} = G + j B = Y \underline{/-\phi}$

Grundzweipole

Idealer Ohmscher Zweipol

Idealer induktiver Zweipol

Idealer kapazitiver Zweipol

Induktivität

Differentialgleichung

$u_{L} = L \frac{d I}{d t}$

Komplexer Widerstand

$\underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})}$

$\underline{Z} = j \omega L$

Komplexes Ohmsches Gesetz

$\underline{U} = j \omega L \underline{I}$

Kapazität

$C = \frac{Q}{U}$

Differentialgleichung

$i_{C} = C \frac{d U}{d t}$

Komplexer Widerstand

$\underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})}$

$\underline{Z} = \frac{1}{j \omega C}$

Komplexes Ohmsches Gesetz

$\underline{U} = \frac{\underline{I}}{j \omega C}$

Zusammenschaltung

Es gelten die Regeln für Parallelschaltung

$\underline{Z} = \frac{1}{\frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2}}$

und Reihenschaltung:

$\underline{Z} = \underline{Z}_1 + \underline{Z}_2$

Die Brüche werden solange erweitert, bis nur ein einfacher Bruch übrig bleibt.
Das Polynom in Zähler und Nenner wird durch Suche der Nullstellen zerlegt.

$\underline{Z} = \frac{ x_1 \cdot (j)^2 + jy_1 + z_1 }{x_2 \cdot (j)^2 + jy_2 + z_2} = \frac{ (a_1 + jb_1) (a_2 + jb_2) }{(a_3 + jb_3) (a_4 + jb_4)}$
Für jeden Term a + jb wird der Betrag und Winkel gebildet und dann zusammen gefasst.

Es kann auch konjugiert komplex erweitert werden, um Real und Imaginärteil zu bilden.

$\underline{Z} = \frac{1}{a + jb} \frac{a - jb}{a - jb} = \frac{a - jb}{a^2 + b^2} = \frac{a}{a^2 + b^2} - \frac{jb}{a^2 + b^2}$

Übung komplexer Widerstand

Zusammenfassung

Wechselspannungsschaltkreise mit Kapazitäten und Induktivitäten können mit der komplexen Rechnung betrachtet werden.
Komplexe Zahlen gibt es in R- und P-Form.
Sie kennen die Differentialgleichung und den komplexen Widerstand für Kapazitäten und Induktivitäten

Rechnen Sie 4 Aufgaben von komplexen Widerständen und schicken Sie dem Dozenten via Email ihr Ergebnis als pdf: Übung komplexer Widerstand

Nächste Vorlesung:

15 Übertragungsfunktion und Simulation

Grundwissen Gleichspannung

Wandeln Sie 72.03 µA in mA und nA um.
Bestimmen Sie für folgende Schaltung alle Spannungen und Ströme.
U(V1) = 3 V; U(V2) = 4 V; R1 = 10 kΩ; R2 = 100 kΩ; R3 = 10
1. Dazu stellen Sie die Knotengleichungen auf.
2. Wenden Sie die Quellenumwandlung und
3. Superposition an.
Wie groß ist die Gesamtleistung der Schaltung.
Bestimmen Sie die Ersatzspannungsquelle bzgl Ausgang VE.

ZweiQuellen.asc

Version 4
SHEET 1 880 680
WIRE 368 160 80 160
WIRE 368 176 368 160
WIRE 80 192 80 160
WIRE 80 288 80 272
WIRE 256 304 144 304
WIRE 368 304 368 256
WIRE 368 304 336 304
WIRE 416 304 368 304
WIRE 368 320 368 304
WIRE 144 336 144 304
WIRE 144 432 144 416
WIRE 368 432 368 400
FLAG 368 432 0
FLAG 80 288 0
FLAG 144 432 0
FLAG 416 304 VE
SYMBOL res 352 160 R0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL res 352 304 R0
SYMATTR InstName R3
SYMATTR Value 10
SYMBOL res 240 320 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 0 56 VBottom 2
SYMATTR InstName R2
SYMATTR Value 100k
SYMBOL voltage 80 176 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value 3
SYMBOL voltage 144 320 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value 4
TEXT 216 216 Left 2 !.op

Bevor Sie Anfangen zu Lesen Bitte notieren Sie ihren Namen und die Uhrzeit
Nach Zwischenschritten und am Ende notieren Sie bitte die Uhrzeit.
U(V1) = 3 V; U(V2) = 4 V; R1 = 10 kΩ; R2 = 100 kΩ; R3 = 10

Durch Übung lernen Sie Aufgaben zu lösen. Wiederholung verkürzt die benötigte Zeit.

Das Dreieck bezeichnet eine Verbindung mit 0 V, Masse, GND, den Bezugspunkt.
Alle Punkte mit dem Dreieck sind verbunden.
Es werden amerikanische Symbole für die Widerstände und Quellen verwendet.

ZweiQuellenKnoten1.asc

Umzeichnen ergibt:
Die Knoten heissen Vx und VE.

ZweiQuellenKnoten2.asc

Version 4
SHEET 1 880 680
WIRE 112 304 32 304
WIRE 160 304 112 304
WIRE 288 304 240 304
WIRE 368 304 288 304
WIRE 416 304 368 304
WIRE 112 320 112 304
WIRE 368 320 368 304
WIRE 32 336 32 304
WIRE 288 336 288 304
WIRE 32 432 32 416
WIRE 112 432 112 400
WIRE 112 432 32 432
WIRE 288 432 288 416
WIRE 288 432 112 432
WIRE 368 432 368 400
WIRE 368 432 288 432
WIRE 288 448 288 432
FLAG 288 448 0
FLAG 416 304 VE
FLAG 112 304 Vx
SYMBOL res 144 320 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 0 56 VBottom 2
SYMATTR InstName R1
SYMATTR Value 5k
SYMBOL res 352 304 R0
SYMATTR InstName R3
SYMATTR Value 10k
SYMBOL res 96 304 R0
SYMATTR InstName R4
SYMATTR Value 10k
SYMBOL current 32 416 R180
WINDOW 0 24 80 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName I1
SYMATTR Value 0.3m
SYMBOL current 288 416 R180
WINDOW 0 24 80 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName I2
SYMATTR Value 50�
TEXT 400 416 Left 2 !.op

Komplexe Widerstände

Übungsaufgaben:

Komplexer Widerstand

Bestimmen Sie den komplexen Widerstand der folgenden Schaltung
R1 = 20 Ω, L1 = 40 mH, C1 = 3 µF, ω = 20 ^-1

RSLPC.asc

Version 4
SHEET 1 880 680
WIRE 32 64 0 64
WIRE 160 64 112 64
WIRE 320 64 160 64
WIRE 160 96 160 64
WIRE 320 112 320 64
WIRE 160 208 160 176
WIRE 160 208 0 208
WIRE 320 208 320 176
WIRE 320 208 160 208
WIRE 160 224 160 208
FLAG 160 224 0
FLAG 0 64 V1
SYMBOL res 128 48 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 20
SYMBOL cap 304 112 R0
SYMATTR InstName C1
SYMATTR Value 3�
SYMBOL ind 144 80 R0
SYMATTR InstName L1
SYMATTR Value 40m
TEXT 16 264 Left 2 !I1 V1 0 SINE(0 1 318) AC 1
TEXT 272 264 Left 2 !;tf V(V1) I1
TEXT 8 304 Left 2 !.ac dec 10 0.1 1000

Weitere Aufgaben: Komplexer Widerstand

Angefangen vom Punkt V1 verfolgt man die Leitungen bis zum Endpunkt, um den Gesamtwiderstand zu bestimmen.
R1 in Reihe mit der Paralellschaltung von L1 und C1.
Alle Elemente werden als Widerstand dargestellt: R, jωL, 1/(jωC)
Eine Reihenschaltung wird als Summe der Widerstände dargestellt.
Eine Paralellschaltung als 1 geteilt durch die Kehrwerte der Widerstände.

$\underline{Z} = R1 + \frac{1}{\frac{1}{j \omega L} + \frac{1}{\frac{1}{j \omega C1}}}$

Bei diesem einfach hin zu schreibenden, aber kompliziert aussehenden Ausdruck werden die mehrfach Brüche von Innen nach Außen elimiert.

$\underline{Z} = R1 + \frac{1}{\frac{1}{j \omega L} + j \omega C1}$

$\underline{Z} = R1 + \frac{j \omega L}{1 + (j \omega)^{2} C1 L1}$

Normalerweise wird der Nenner konjugiert komplex erweitert, um zu einer Zahl zu kommen und Realteil und Imaginärteil darzustellen.
Hier ergibt sich aus j²= -1 nur ein Realteil.

Jetzt können Werte eingesetzt werden.
Man rechnet so lange wie möglich symbolisch, um Zusammenhänge zu erkennen und Fehler einfacher zu verfolgen und zu beheben.

$\underline{Z} = 20 \Omega + j 0.8 \Omega = 20.016 \Omega \angle 2.29°$

Die Lösung kann man mit der Webseite verifizieren: Komplexer Widerstand
Man sucht sich die richtige Topologie und setzt dann die richtigen Werte ein.

Die Lösung kann man auch mit einer LTSPICE AC Simulation V(v1)/I(R1) verifizieren.

2020 Elektronik 10 Komplexe Rechnung Prof. Dr. Joerg Vollrath

Elektronik

10 Komplexe Rechnung

Prof. Dr. Jörg Vollrath

Video der 15. Vorlesung 24.11.2020

Übersicht

Audioverstärker

Projekt 2. Semester Audioverstärker

Messung mit R, L und C bei 20 kHz

Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Fragen:

Oszilloskop

Messung

Zeigerdarstellung

Komplexe Zahlen und Rechnung

R-Form und P-Form

R-Form

P-Form

Rechnung für Sinusförmige Wechselgrößen

Ohmsches Gesetz im Komplexen

Grundzweipole

Induktivität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Kapazität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Zusammenschaltung

Zusammenfassung

Nächste Vorlesung:

Grundwissen Gleichspannung

Komplexe Widerstände

Übungsaufgaben: