Elektronik15 Übertragungsfunktion und SimulationProf. Dr. Jörg Vollrath10 Komplexe Rechnung |

|
Video der 16. Vorlesung
|
Länge: |
0:0:0 Übertragungsfunktion, LTSPICE 0:0:25 Stromgleichung, Ohmsches Gesetz 0:3:33 Graphische Darstellung 0:5:6 Das Maß in dB, 20 log(Ua/Ue) 0:8:3 Das Maß der Übertragungsfunktion 0:11:21 Einzelterme 0:13:21 Knick in der Gerade Im{} = Re{} 0:15:21 Punktweise Addition 0:17:41 Übertragungsfunktion stellt die Frequnezabhängigkeit dar 0:20:47 Schaltungssimulator LTSPICE 0:22:41 Spannungsquelle 0:25:31 Knotennamen setzen 0:28:1 Stromrichtung im Widerstand 0:30:11 LTSPICE Bücher und Download 0:31:31 Netzliste 0:35:21 Simulationsanweisungen 0:36:11 Sinusfunktion 0:41:1 AC Simulation der Übertragungsfunktion 0:44:41 3 dB Eckfrequenz, Re{} = Im{}, wurzel(2) 0:48:37 Ergebnis Eckfrequenz 0:54:12 LTSPICE verifiziert die Rechnung 0:54:57 Phasendarstellung 0:57:27 Ansatz für die Übertragungsfunktion 1:0:17 Anwendung Frequenzweiche 1:4:57 LTSPICE Schaltungen herunterladen |
Übersicht Elektronik
- Elemente mit 2 Anschlüssen
- Aktiv: Stromquelle, Spannungsquelle
- Passiv: R, L, C
- Reale Quellen: Innenwiderstand
- Verhalten
- Statische Gleichung, Kennlinie: I(U)
Übertragungsfunktion: U1/U2(jw)
Simulation: LTSPICE
Messung: Oszilloskop
- Elemente mit 4 Anschlüssen
- Verstärker: Eingang, Ausgang
- Gesteuerte Quellen
- Nichtlineare Elemente
- Dioden
- Transistoren
- Ersatzschaltbilder und Linearisierung
Diese Präsentation beschäftigt sich mit dem Schaltungsentwurf und der Übertragungsfunktion.
Die Eigenschaften einer Zusammenschaltung von Quellen, Widerständen, Kapazitäten und Induktivitäten soll nicht nur mathematisch für eine Gleichspannung, sondern auch für Wechselspannungen verschiedener Frequenzen beschrieben werden (Übertragungsfunktion).
Die mathematische Beschreibung wird durch Simulation, einen Schaltungsaufbau und eine Messung ergänzt.
Die mathematische Rechnung, die Simulation und die Messung sollen die gleichen Ergebnisse liefern.
Dieses Vorgehen bezeichnet man als Schaltungsentwurf.
Die obige Liste zeigt ausserdem die nächsten Themen und Bauelemente dieser Vorlesung: Verstärker und nichtlineare Elemente, die in den kommenden Vorlesungen behandlet werden.
Die Eigenschaften einer Zusammenschaltung von Quellen, Widerständen, Kapazitäten und Induktivitäten soll nicht nur mathematisch für eine Gleichspannung, sondern auch für Wechselspannungen verschiedener Frequenzen beschrieben werden (Übertragungsfunktion).
Die mathematische Beschreibung wird durch Simulation, einen Schaltungsaufbau und eine Messung ergänzt.
Die mathematische Rechnung, die Simulation und die Messung sollen die gleichen Ergebnisse liefern.
Dieses Vorgehen bezeichnet man als Schaltungsentwurf.
Die obige Liste zeigt ausserdem die nächsten Themen und Bauelemente dieser Vorlesung: Verstärker und nichtlineare Elemente, die in den kommenden Vorlesungen behandlet werden.
Schaltungsentwurf
Beim Schaltungsentwurf soll ein Verhalten, das z.B. durch eine Gleichung beschrieben wird
mit diskreten oder integrierten Schaltkreisen auf einer Platine in einem Gehäuse realisiert werden.
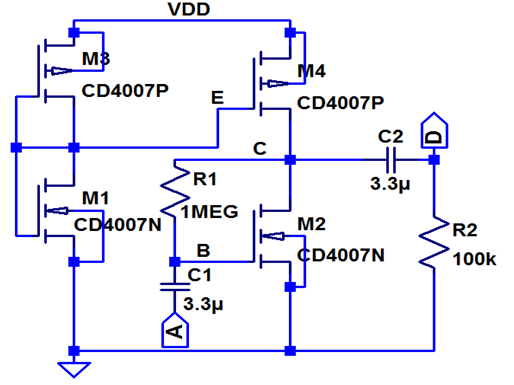
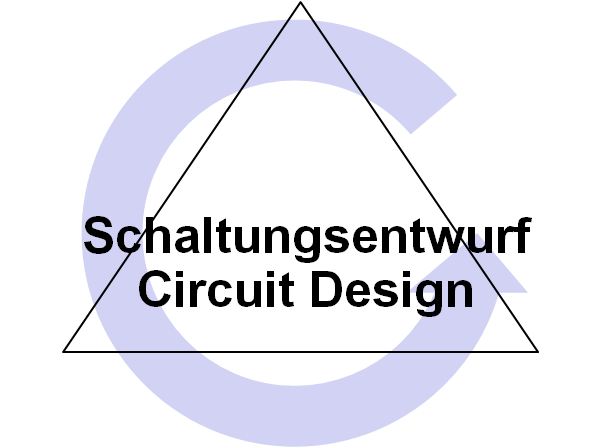
Eine typische Übertragungsfunktion, die ein elektrisches Verhalten beschreibt, ist in der Mitte abgebildet.
Man kann diese Übertragungsfunktion mit integrierten Schaltungen (links oben) oder einer Transistorschaltung auf einer Platine (rechts unten) realisieren. Dazu erstellt man einen geeigneten Schaltplan (links unten) und verifiziert die Funktionsweise mit einer Simulation und mit einem Steckbrettaufbau (rechts oben).
Eine typische Übertragungsfunktion, die ein elektrisches Verhalten beschreibt, ist in der Mitte abgebildet.
Man kann diese Übertragungsfunktion mit integrierten Schaltungen (links oben) oder einer Transistorschaltung auf einer Platine (rechts unten) realisieren. Dazu erstellt man einen geeigneten Schaltplan (links unten) und verifiziert die Funktionsweise mit einer Simulation und mit einem Steckbrettaufbau (rechts oben).
Schaltungsentwurf
Model
| ||
 | ||
Simulation
|
Measurement
|
Lernziele
Sie können eine Kennlinie und Übertragungsfunktion simulieren.
Sie können mit der Simulation Berechnungen verifizieren.
Sie können abschätzen, wie sich ihre Schaltung verhalten wird.
Sie können komplexere, realitätsnähere, nichtlineare Modelle in der Simulation verwenden.
Summation von Sinusfunktionen
Motivation Übertragungsfunktion
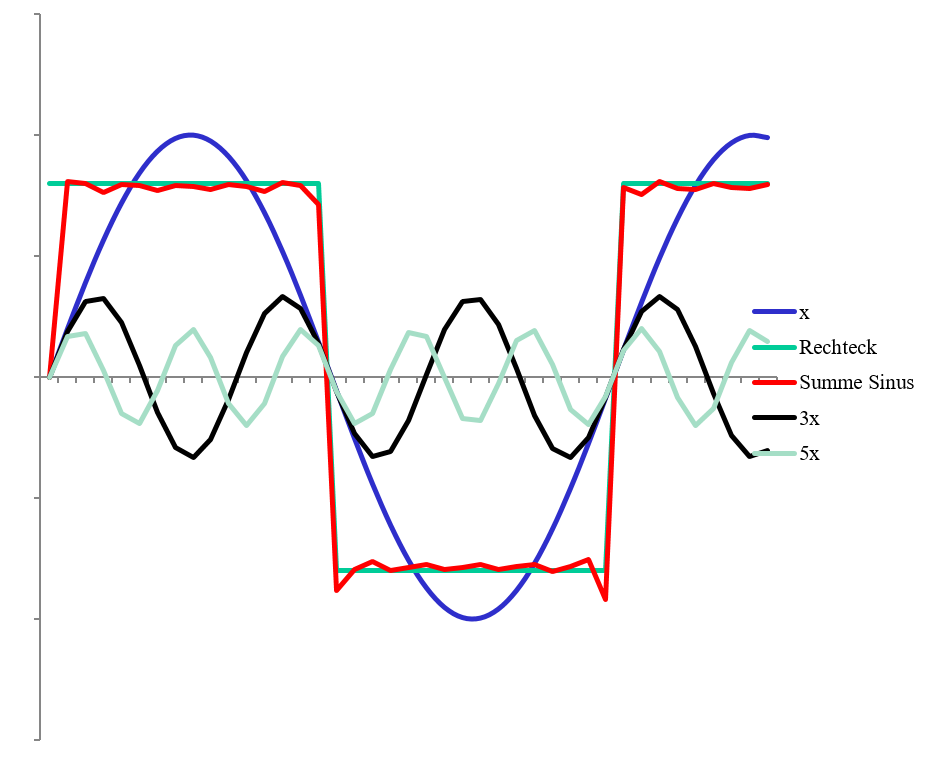
\( \sum{\frac{1}{n} sin(nx) } \)
n =1,3,5,7,..
Werkzeug: Fouriertransformation
Numerisches Verfahren in Excel
Beispiel: Berechnung und LTSPICE Simulation RL
Wie ändert sich die Ausgangsspannung Uout mit der Frequenz?
|
R1 = 80 Ω R2 = 8 Ω L1 = 15 µH UE = 250 mV Gesucht: Uout(1 kHz, 10 kHz, 100 kHz, 300 kHz, 1 MHz, 10 MHz)
\( \frac{U_{out}}{U_E} = \frac{R2 + j \omega L1}{R1 + R2 + j \omega L1}\)
|
Spannungsteiler:
Überall fliesst der gleiche Strom.
\( I = \frac{U_{out}}{R2 + j \omega L1} = \frac{U_{E}}{R1 + R2 + j \omega L1} \)
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\)
Betrachtung für kleine Frequenzen:
\( \frac{U_{out}}{U_E} = \frac{j 0 + \frac{R2}{L1} }{j 0 + \frac{R1 + R2}{L1} }\)
\( \frac{U_{out}}{U_E} = \frac{R2}{L1} * \frac{L1}{R1 + R2}\)
\( \frac{U_{out}}{U_E} = \frac{R2}{R1 + R2} = 0.09 < 1 \)
Betrachtung für grosse Freqenzen:
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\)
\( \frac{U_{out}}{U_E} = \frac{1 + \frac{R2}{ j \omega L1} }{1 + \frac{R1 + R2}{L1 j \omega}} \)
\( \frac{U_{out}}{U_E} = \frac{1 + \frac{R2}{ j \infty L1} }{1 + \frac{R1 + R2}{L1 j \infty}} = 1 \)
Überall fliesst der gleiche Strom.
\( I = \frac{U_{out}}{R2 + j \omega L1} = \frac{U_{E}}{R1 + R2 + j \omega L1} \)
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\)
Betrachtung für kleine Frequenzen:
\( \frac{U_{out}}{U_E} = \frac{j 0 + \frac{R2}{L1} }{j 0 + \frac{R1 + R2}{L1} }\)
\( \frac{U_{out}}{U_E} = \frac{R2}{L1} * \frac{L1}{R1 + R2}\)
\( \frac{U_{out}}{U_E} = \frac{R2}{R1 + R2} = 0.09 < 1 \)
Betrachtung für grosse Freqenzen:
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\)
\( \frac{U_{out}}{U_E} = \frac{1 + \frac{R2}{ j \omega L1} }{1 + \frac{R1 + R2}{L1 j \omega}} \)
\( \frac{U_{out}}{U_E} = \frac{1 + \frac{R2}{ j \infty L1} }{1 + \frac{R1 + R2}{L1 j \infty}} = 1 \)
Übertragungsfunktion und Maß
Übertragungsfunktion (Transfer function)
\( \underline{T} (j\omega) = \frac{\underline{U}_{out}}{\underline{U}_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} } = \frac{j \omega + s_{N1} }{j \omega + s_{P1} } \)
Die Übertragungsfunktion setzt sich aus Faktoren (jω + sNi) und (jω + sPi)-1 zusammen.
Das Maß in Dezibel ist definiert als
\( 20 log_{10} \left| \frac{\underline{U}_A}{\underline{U}_E} \right| dB \)
Die Übertragungsfunktion als Maß ist dann:
\( A(j\omega) = 20 log_{10} \left| j \omega + \frac{R2}{L1} \right| dB - 20 log_{10} \left| j \omega + \frac{R1 + R2}{L1} \right| dB \)
Die Übertragungsfunktion stellt das Maß in Dezibel (dB) und die Phase über der logarithmischer Frequenz dar.
Durch die obige Form kann man die Übertragungsfunktion als Maß mit einer logarithmischen Frequenz schnell zeichnen.
Man beachte dass negative Vorzeichen beim Maß für den Nenner.
Jede Übertragungsfunktion wird so umgeformt, dass im Zähler und Nenner ein Polynom von jω steht.
Durch suche der Nullstellen kann man dieses Polynom dann zerlegen.
z.B. (jω)2 + 2 Re jω + Re2 = (jω + Re )2
Die Übertragungsfunktion setzt sich dann aus einzelnen Termen von jω zusammen.
Die einzelnen Terme werden graphisch addiert (subtrahiert).
Da jω in der Elektrotechnik als s abgekürzt wird und der obige Term (jω + sNi) sich wie eine Nullstelle (Ni verhält, ergibt sich der Bezeichner sNi.
Für den Nenner (jω + sPi)-1 ergibt sich eine Polstelle (Pi)
Maße in Dezibel, die man sich merken sollte:
20 dB entsprechen einem Faktor 10.
6 dB entsprechen einem Faktor 2.
3 dB entsprechen einem Faktor \( \sqrt{2} \).
0 dB entsprechen dem Faktor 1.
Durch die obige Form kann man die Übertragungsfunktion als Maß mit einer logarithmischen Frequenz schnell zeichnen.
Man beachte dass negative Vorzeichen beim Maß für den Nenner.
Jede Übertragungsfunktion wird so umgeformt, dass im Zähler und Nenner ein Polynom von jω steht.
Durch suche der Nullstellen kann man dieses Polynom dann zerlegen.
z.B. (jω)2 + 2 Re jω + Re2 = (jω + Re )2
Die Übertragungsfunktion setzt sich dann aus einzelnen Termen von jω zusammen.
Die einzelnen Terme werden graphisch addiert (subtrahiert).
Da jω in der Elektrotechnik als s abgekürzt wird und der obige Term (jω + sNi) sich wie eine Nullstelle (Ni verhält, ergibt sich der Bezeichner sNi.
Für den Nenner (jω + sPi)-1 ergibt sich eine Polstelle (Pi)
Maße in Dezibel, die man sich merken sollte:
20 dB entsprechen einem Faktor 10.
6 dB entsprechen einem Faktor 2.
3 dB entsprechen einem Faktor \( \sqrt{2} \).
0 dB entsprechen dem Faktor 1.
Untersuchung der Übertragungsfunktion als Maß
\( A(j\omega) = 20 log_{10} \left| j \omega + \frac{R2}{L1} \right| dB - 20 log_{10} \left| j \omega + \frac{R1 + R2}{L1} \right| dB \)
Für die Zeichnung untersucht man für jeden Term: jω + Re, ob ω viel größer als der Realteil Re ist oder viel kleiner.
j ω >> Re: \( 20 log_{10} | j \omega | \)
Wenn sich ω um den Faktor 10 ändert, ändert sich das Maß um 20 dB. Eine Gerade mit Steigung 20 dB pro Dekade (Faktor 10).
j ω << Re : \( 20 log_{10} | Re | \)
Der Betrag ist konstant. Eine Gerade mit Steigung 0.
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
3dB Eckfrequenz
Untersuchung von
\( 20 log_{10} \left| j \omega + s_{N1} \right| dB \)
für | jω | = Re
\( 20 log_{10} \left( \sqrt{ Re^2 + Re^2} \right) dB = 20 log_{10} \left( \sqrt{2} \cdot Re \right) dB \)
\( = 20 log_{10} \left( \sqrt{2} \right) dB + 20 log_{10} \left(Re \right) dB \)
\( = 3 dB + 20 log_{10} \left(Re \right) dB \)
Die reale Übertragungsfunktion als Maß weicht an der Eckfrequenz um 3 dB von den idealisierten Geraden ab.
Der Phasengangs der Übertragungsfunktion
Untersuchung von
\( \underline{T} (j\omega) = \frac{\underline{U}_{out}}{\underline{U}_E} = \frac{j \omega + Re_Z }{j \omega + Re_N } = \frac{j \omega + s_{N1} }{j \omega + s_{P1} } \)
\( \phi (j\omega) = atan\left(\frac{\omega}{Re_Z}\right) - atan\left(\frac{\omega}{Re_N}\right)\)
j ω >> Re: \( atan\left(\frac{\omega}{Re}\right) = 90° \)
j ω << Re : \( atan\left(\frac{\omega}{Re}\right) = 0° \)
j ω = Re: \( atan\left(\frac{Re}{Re}\right) = 45° \)
Für die Zeichnung untersucht man für jeden Term: jω + Re,
ob ω viel größer als der Realteil Re ist oder viel kleiner.
Für j ω >> Re ist der Winkel konstant 90° (π/2).
Für j ω << Re ist der Winkel konstant 0° (0).
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
Für j ω = Re: ist der Winkel ist 45° (π/4).
Bei einem Faktor 10 für ω ist jω >> Re oder jω << Re.
Man kann beim Zeichnen also die Punkte für f3dB, 1/10 f3dB und 10 f3dB einzeichnen.
Die Umrechnung von Bogenmaß in Grad erfolgt mit:
π = 180°
\( \phi_B = \frac{\phi_{Grad}}{180} \cdot \pi \)
\( \phi_{Grad} = \frac{\phi_B}{\pi} \cdot 180° \)
Für j ω >> Re ist der Winkel konstant 90° (π/2).
Für j ω << Re ist der Winkel konstant 0° (0).
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
Für j ω = Re: ist der Winkel ist 45° (π/4).
Bei einem Faktor 10 für ω ist jω >> Re oder jω << Re.
Man kann beim Zeichnen also die Punkte für f3dB, 1/10 f3dB und 10 f3dB einzeichnen.
Die Umrechnung von Bogenmaß in Grad erfolgt mit:
π = 180°
\( \phi_B = \frac{\phi_{Grad}}{180} \cdot \pi \)
\( \phi_{Grad} = \frac{\phi_B}{\pi} \cdot 180° \)
Übertragungsfunktion und Maß des Beispiels
|
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\) \( 20 log_{10} | j \omega + \frac{R2}{L1} | \) \( - 20 log_{10} | {j \omega + \frac{R1 + R2}{L1} } | \) \( \frac{R2}{2 \pi L1 } = 86 kHz \) \( \frac{R1 + R2}{2 \pi L1} = 934 kHz \) \( 20 log | \frac{R2}{L1} | = 114 dB \) und \( - 20 log | {\frac{R1 + R2}{L1} } | = - 135 dB \) |
\( \frac{R2}{L1} = 533E3 s^{-1} \)
\( \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Man kann nun die 2 Punkte eintragen:
P1(533E3 s-1, 135 dB) und P2(5866E3 s-1, 114 dB)
Zwischen diesen Punkten liegt näherungsweise eine Gerade mit Steigung 20dB/Dekade (Faktor 10).
Rechts und links der Punkte ist das Maß konstant (jω<<Re).
\( \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Man kann nun die 2 Punkte eintragen:
P1(533E3 s-1, 135 dB) und P2(5866E3 s-1, 114 dB)
Zwischen diesen Punkten liegt näherungsweise eine Gerade mit Steigung 20dB/Dekade (Faktor 10).
Rechts und links der Punkte ist das Maß konstant (jω<<Re).
LTSPICE
- Schaltungssimulation:
Erleichterte Rechnung - Überprüfung einer Rechnung
- Schaltplaneingabe
- Spannung, Strom, Übertragungsfunktion
Simulation
LTSPICE
Beispiel: LTSPICE AC Simulation RL
|
\( \frac{U_{out}}{U_E} = \frac{R2 + j \omega L1}{R1 + R2 + j \omega L1}\) R1 = 80 Ω R2 = 8 Ω L1 = 15 µH AC Simulation: Spannungsquelle: AC 1 Simulation .AC |

|
\( \omega_{1 3dB} = \frac{R2}{L1} = 533E3 s^{-1} \)
\( f_{1 3dB} = \frac{\omega_{1 3dB}}{2 \pi } = 84 kHz \)
\( \omega_{2 3dB} = \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
\( f_{2 3dB} = \frac{\omega_{2 3dB}}{2 \pi } = 933 kHz \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Die durchgezogene Linie gehört zur linken Achse und ist das Mass.
Die gestrichelte Linie ist die Phase und gehört zur rechten Achse.
Bei der Eckfrequenz hat sich der Betrag um 3dB geändert und die Phase ist 45 °.
|jω| = Re
Betrag: \( 20 log \sqrt{2} = 3 dB \)
Phase: arctan(jω/Re) = 45°.
\( f_{1 3dB} = \frac{\omega_{1 3dB}}{2 \pi } = 84 kHz \)
\( \omega_{2 3dB} = \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
\( f_{2 3dB} = \frac{\omega_{2 3dB}}{2 \pi } = 933 kHz \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Die durchgezogene Linie gehört zur linken Achse und ist das Mass.
Die gestrichelte Linie ist die Phase und gehört zur rechten Achse.
Bei der Eckfrequenz hat sich der Betrag um 3dB geändert und die Phase ist 45 °.
|jω| = Re
Betrag: \( 20 log \sqrt{2} = 3 dB \)
Phase: arctan(jω/Re) = 45°.
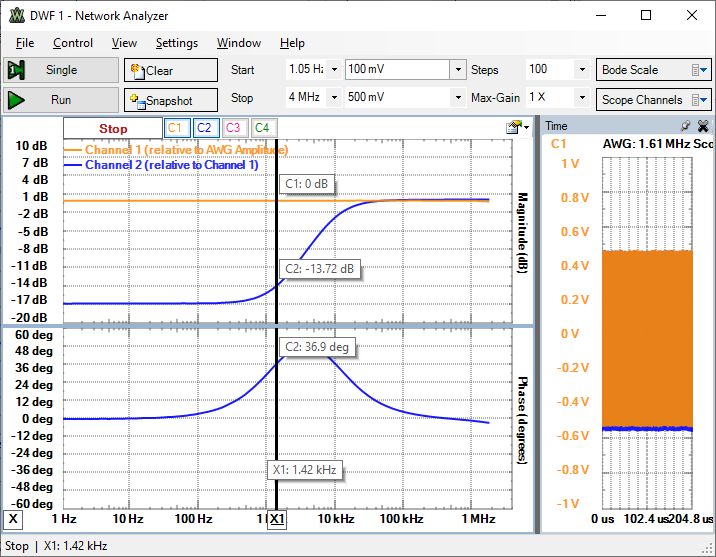
Beispiel: Messung Übertragungsfunktion RL
\( \frac{U_{out}}{U_E} = \frac{R_i + j \omega L}{R + R_i + j \omega L}\)
Waveforms: More Instruments Network Analyzer |
|
R = 100 Ohm, L = 2.18 mH (Aufdruck)
Av = -16.65 dB
v = 0.147
\( v = \frac{U_a}{U_e} = \frac{R_i}{R + R_i}\)
\( R_i = \frac{ v R}{1 - v} = 17.2 \Omega \)
f3dB1 = 1.4 kHz
\( f_{3dB1} = \frac{R_i}{2 \pi L} \)
\( L = \frac{R_i}{2 \pi f_{3dB1}} = 1.95 mH \)
f3dB2 = 9.33 kHz
\( f_{3dB2} = \frac{R_i + R}{2 \pi L} \)
\( L = \frac{R_i + R}{2 \pi f_{3dB2}} = 2.00 mH \)
Av = -16.65 dB
v = 0.147
\( v = \frac{U_a}{U_e} = \frac{R_i}{R + R_i}\)
\( R_i = \frac{ v R}{1 - v} = 17.2 \Omega \)
f3dB1 = 1.4 kHz
\( f_{3dB1} = \frac{R_i}{2 \pi L} \)
\( L = \frac{R_i}{2 \pi f_{3dB1}} = 1.95 mH \)
f3dB2 = 9.33 kHz
\( f_{3dB2} = \frac{R_i + R}{2 \pi L} \)
\( L = \frac{R_i + R}{2 \pi f_{3dB2}} = 2.00 mH \)
Zusammenfassung
- Sie können LTSPICE zur Verifikation ihrer Rechnung und einer Schaltung verwenden.
- Sie können eine Übertragungsfunktion darstellen und Eckfrequenzen ablesen und berechnen.
- Übung zur Übertragungsfunktion
Diese Vorlesung:
LTSPICE
Nächste Vorlesung:
16 Abstraktion und Modelle