Elektronik

16 Modelle

Prof. Dr. Jörg Vollrath

15 Abstraktion Simulation

Video der 17. Vorlesung 1.12.2020

Länge: 01:28:01

0:0:10 Komplexer Widerstand

0:5:16 Internet Übung komplexer Widerstand

0:10:32 Eckfrequenz, Übertragungsfunktion

0:21:46 Komplexer Widerstand

0:25:28 Gleichung, Simulation, Messung von Bauteilen

0:28:54 Lineare Modelle

0:31:41 Widerstandsmessung

0:34:54 Kapazitätsmessung Anwendung Differentialgleichung

0:40:48 Induktivitätsmessung

0:43:4 Electronic Explorer

0:47:40 Spannungsquellen, Stromquellen

0:48:39 Ideale Spannungsquelle

0:51:54 Ideale Stromquelle

0:53:9 Reale Spannungsquelle

1:1:9 Electronic Explorer Spannungsquelle

1:4:39 Quellenumwandlung

1:7:43 Wechselspannungsquelle

1:10:8 Frequenzgang

1:11:14 Gesteuerte Quellen

1:13:58 Zusammenfassung

Video Quellenmessung 2.6.2022

Länge: 20:00

Video Bodediagram RC Messung 2.6.2022

Länge: 10:00

Übersicht

Elemente mit 2 Anschlüssen

Aktiv: Stromquelle, Spannungsquelle
Reale Quellen: Innenwiderstand
Passiv: R, L, C

Verhalten

Statische Gleichung, Kennlinie: I(U)
Übertragungsfunktion: U1/U2(jw)
Simulation: LTSPICE
Messung: Oszilloskop

Elemente mit 4 Anschlüssen

Verstärker: Eingang, Ausgang
Gesteuerte Quellen

Nichtlineare Elemente

Dioden
Transistoren
Ersatzschaltbilder und Linearisierung

Lernziele

Sie kennen Modelle von Bauelementen

Sie können von einem Bauteil ein Modell erstellen

Statische und dynamische UI-Messung am Eingang und Ausgang.
Zerlegung in R, L, C und gesteuerte Quellen.

Lineare Modelle

Einfache 2-polige lineare Bauelemente

R statische Kennlinie U = R · I
L, C: $U = - L \frac{dI}{dt}$ $I = C \frac{dU}{dt}$
U = j ω L · I ; $U = \frac{I}{j \omega C}$
U, I :Spannungsquellen, Stromquellen

Kombinierte Bauelemente

Reale Quellen: U, I, Z
Tiefpass, Hochpass: R, C, L

4-polige lineare Bauelemente

Gesteuerte Quellen

Modelle.asc

Version 4
SHEET 1 880 680
WIRE 96 144 48 144
WIRE 192 144 176 144
WIRE 288 144 224 144
WIRE 352 144 288 144
WIRE 400 144 384 144
WIRE 496 144 480 144
WIRE 512 144 496 144
WIRE 48 160 48 144
WIRE 224 160 224 144
WIRE 288 160 288 144
WIRE 496 160 496 144
WIRE 48 256 48 240
WIRE 192 256 48 256
WIRE 224 256 224 240
WIRE 288 256 288 240
WIRE 288 256 224 256
WIRE 352 256 288 256
WIRE 496 256 496 224
WIRE 496 256 384 256
WIRE 512 256 496 256
WIRE 128 320 80 320
WIRE 272 320 224 320
WIRE 448 320 352 320
WIRE 128 352 128 320
WIRE 224 352 224 320
WIRE 128 464 128 432
WIRE 128 464 80 464
WIRE 224 464 224 432
WIRE 448 464 224 464
FLAG 128 320 Vinp
FLAG 128 464 Vinm
SYMBOL res 80 -16 R0
SYMATTR InstName R1
SYMBOL ind 160 -16 R0
SYMATTR InstName L1
SYMBOL cap 240 0 R0
SYMATTR InstName C1
SYMBOL voltage 336 -16 R0
SYMATTR InstName V1
SYMBOL current 432 0 R0
SYMATTR InstName I1
SYMBOL current 224 160 R0
SYMATTR InstName I2
SYMBOL res 192 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMBOL res 272 144 R0
SYMATTR InstName R3
SYMBOL voltage 48 144 R0
SYMATTR InstName V2
SYMBOL bv 224 336 R0
SYMATTR InstName B1
SYMATTR Value V={VU}*(V(Vinp)-V(Vinm))
SYMBOL res 112 336 R0
SYMATTR InstName R4
SYMBOL res 368 304 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R5
SYMBOL res 496 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R6
SYMBOL cap 480 160 R0
SYMATTR InstName C2

Widerstandsmessung

UI Kennlinie

Strommessung
Magnetfeld, Messwiderstand
Lineare UI-Kennlinie
Steigung ist der Leitwert

$R = \frac{U}{I} = \frac{U2}{\frac{U_1 - U_2 }{R_{Mess}}}$

$R = \frac{U2 \cdot R_{Mess} }{U_1 - U_2}$

WiderstandsmessungA.asc

Version 4
SHEET 1 880 680
WIRE 144 48 80 48
WIRE 320 48 224 48
WIRE 320 80 320 48
WIRE 80 96 80 48
WIRE 80 192 80 176
WIRE 192 192 80 192
WIRE 320 192 320 160
WIRE 320 192 192 192
WIRE 192 208 192 192
FLAG 192 208 0
FLAG 80 48 U1
FLAG 320 48 U2
SYMBOL voltage 80 80 R0
SYMATTR InstName V1
SYMATTR Value 1
SYMBOL res 240 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Rmess
SYMATTR Value 100
SYMBOL res 304 64 R0
SYMATTR InstName RX
SYMATTR Value 80
TEXT 80 248 Left 2 !.dc V1 -1 1 0.01

Der Messwiderstand muss in der Größenordnung des zu messenden Widerstands sein.
Bild: Messaufbau und xy-Darstellung Electronic Explorer

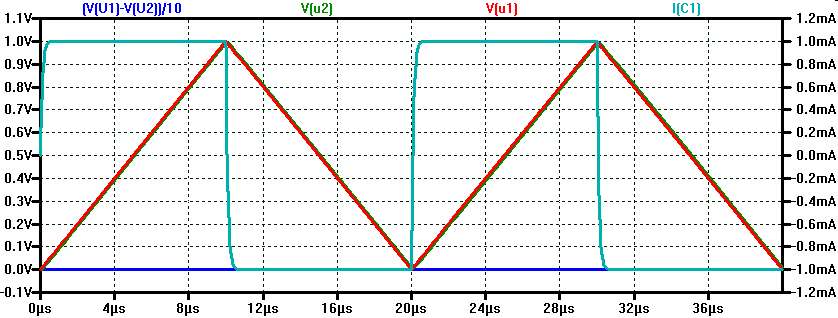
Kapazitätsmessung dU/dt

Strommessung

mit Spannungsrampe

Messwiderstand
Lineare UI-Kennlinie
Steigung ist der Leitwert

$I = C \frac{dU}{dt}$

$C = \frac{I \cdot dt}{dU} = \frac{ 1 mA \cdot 10 \mu s }{1 V} = 10 nF$

KapazitaetMessung.asc

Version 4
SHEET 1 880 680
WIRE 144 48 80 48
WIRE 320 48 224 48
WIRE 320 80 320 48
WIRE 80 96 80 48
WIRE 80 192 80 176
WIRE 192 192 80 192
WIRE 320 192 320 144
WIRE 320 192 192 192
WIRE 192 208 192 192
FLAG 192 208 0
FLAG 80 48 U1
FLAG 320 48 U2
SYMBOL voltage 80 80 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value PULSE(0 1 0 10u 10u 0 20u 10)
SYMBOL res 240 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Rmess
SYMATTR Value 100
SYMBOL cap 304 80 R0
SYMATTR InstName C1
SYMATTR Value 10n
TEXT 104 248 Left 2 !.tran 40u

Der Messwiderstand muss in der Größenordnung des zu messenden Widerstands sein.
Bild: Messaufbau und xy-Darstellung Electronic Explorer

Induktivitätsmessung mit Übertragungsfunktion

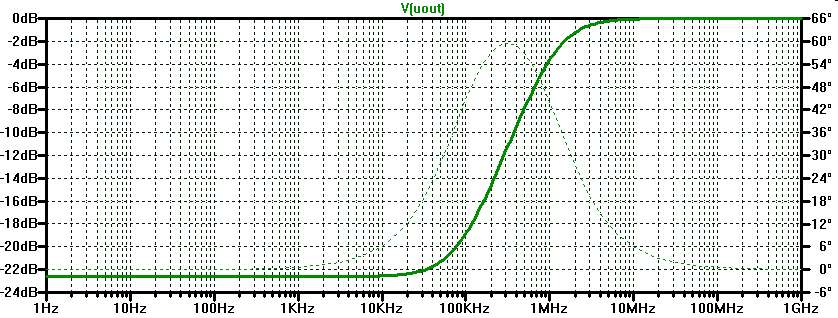
$\frac{U_{out}}{U_E} = \frac{R_{L1} + j \omega L_1}{R_{L1} + R_{Mess} + j \omega L_1}$
R_Mess = 100 Ω
U_{E AC} = 1 V

ω = 0 s^-1

$\frac{U_{out}}{U_E} = \frac{R_{L1}}{R_{L1} + R_{Mess}}$

$R_{L1} = \frac{R_{Mess}}{ \frac{U_E}{U_{out}} - 1 } = \frac{100 \Omega}{ \frac{1 V}{0.074} - 1 } = 8 \Omega$

Eckfrequenz: 3dB = 20 log

$\sqrt{2}$ und φ = 45°

$L_{1} = \frac{R_{L1} + R_{Mess}}{\omega} = \frac{R_{L1} + R_{Mess}}{2 \pi f_{3dB}}$

Induktivitaetsmess.asc

Version 4
SHEET 1 880 680
WIRE 176 112 112 112
WIRE 320 112 256 112
WIRE 400 112 320 112
WIRE 496 112 480 112
WIRE 496 144 496 112
WIRE 112 176 112 112
WIRE 112 288 112 256
WIRE 496 288 496 224
FLAG 112 288 0
FLAG 320 112 Uout
FLAG 496 288 0
SYMBOL voltage 112 160 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V1
SYMATTR Value SINE(0 1 1k)
SYMBOL res 272 96 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RMess
SYMATTR Value 100
SYMBOL res 496 96 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RL1
SYMATTR Value 8
SYMBOL ind 480 128 R0
SYMATTR InstName L1
SYMATTR Value 15�
TEXT 288 192 Left 2 !;tran 4m
TEXT 288 224 Left 2 !.ac dec 10 1 1G

LTSPICE Übertragungsfunktion:

$\frac{U_{out}}{U_E} = (1 Hz) = -23 dB = 0.074$

$L_{1} = \frac{8 \Omega + 100 \Omega }{2 \pi 1 MHz} = 15 \mu H$

Laborarbeitsplatz Electronic Explorer

Oszilloskop
4 Kanäle: AC, DC
Funktionsgenerator
2 Kanäle
Spannungsversorgung
VP+. VP-, Vcc
Breadboard
Schaltungsaufbau

Quellen: DC Gleichspannung

Reale Spannungsquelle

$R_I = \frac{U_L}{I_K}$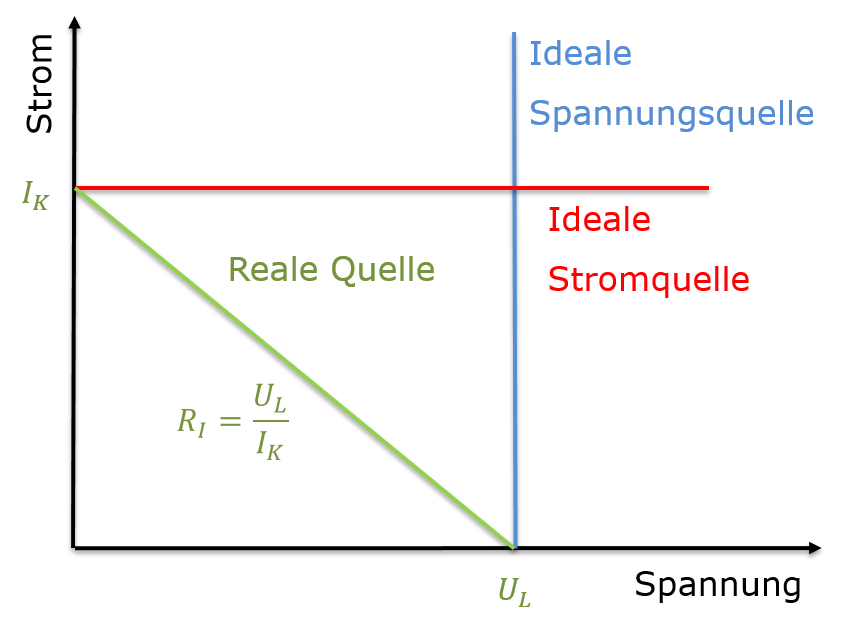

Arbitrary Waveform Generator

Electronic Explorer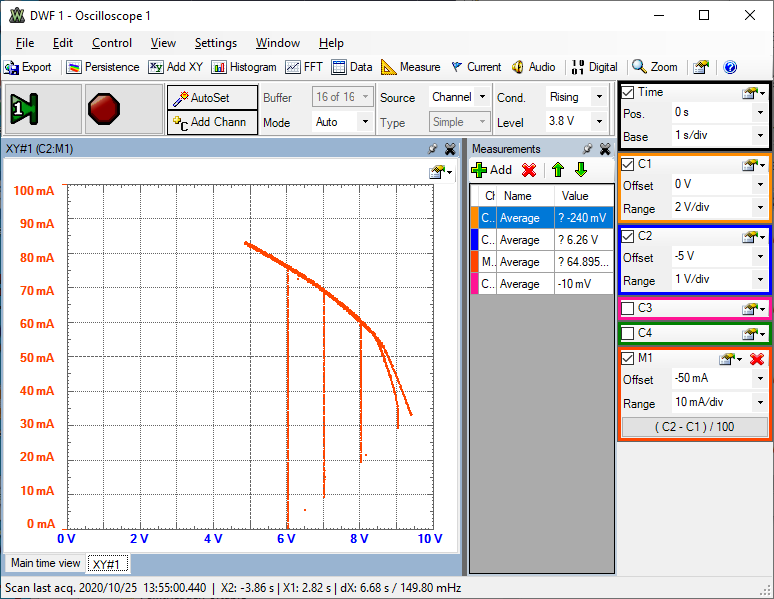

Reale Spannungsquelle

Gleichspannung:

Leerlaufspannung
Kurzschlussstrom
Innenwiderstand

Arbitrary Waveform Generator

Electronic Explorer

An die zu messende Spannungsquelle wird ein Strommesswiderstand und eine variable Spannungsquelle angeschlossen.

Die Kennlinien von Quellen

Bei der Kennlinie wird Spannung und Strom gegeneinander aufgetragen.
Eine ideale Spannungsquelle wird bei verschiedenen Lasten immer die Leerlaufspannung UL haben. Trägt man den Strom (y-Achse) über der Spannung (x-Achse) an erhält man eine senkrechte Gerade.

Die Kennlinie einer realen Quelle erhält man bei der Betrachtung einer Spannungsquelle UL mit einem Innenwiderstand RI unter Belastung mit verschiedenen Widerständen RX.

$I(U) = \frac{UL}{RI + RX} = \frac{U}{RX}$

UL RX = U (RI + RX)
RX ( UL - U) = U · RI

$RX = \frac{U \cdot RI}{UL - U}$

$I(U) = \frac{U}{\frac{U \cdot RI}{UL - U}} = \frac{UL - U}{RI}$

Messung

Das Bild zeigt eine Ausgangsspannungsmessung von AWG1 des Electronic Explorer Boards.
Bis zu einem gewissen Strom verhält sich der Generator wie eine ideal Spannungsquelle U = konstant.
Bei sehr grossen Strömen nimmt die Ausgangsspannung ab. Anhand der Steigung kann man den Innenwiderstand R_I bestimmen.

$R_I = \frac{dU}{dI} = \frac{1 V}{5 mA} = 200 \Omega$

Man misst die reale Spannungsquelle mit verschiedenen Lasten (unterschiedliche Ströme) und kann so den Innenwiderstand bestimmen.
Das Schaltbild zeigt eine typische Messanordnung mit realer Spannungsquelle links (V1, RI) und Messeinrichtung rechts (V2, RMess). Der Messwiderstand dient der Strommessung. Man misst den Spannungsabfall und berechnet mit dem ohmschen Gesetz den Strom.

QuellenMess.asc

Version 4
SHEET 1 940 680
WIRE 160 96 112 96
WIRE 352 96 240 96
WIRE 448 96 352 96
WIRE 560 96 528 96
WIRE 560 160 560 96
WIRE 112 176 112 96
WIRE 112 288 112 256
WIRE 560 288 560 240
FLAG 112 288 0
FLAG 352 96 Uout
FLAG 560 288 0
SYMBOL voltage 112 160 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value 5
SYMBOL res 256 80 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RI
SYMATTR Value 10
SYMBOL voltage 560 144 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value PULSE(-5 5 0 2m 2m 0 4m)
SYMBOL res 544 80 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RMess
SYMATTR Value 100
TEXT 368 208 Left 2 !.tran 4m

AC Wechselspannungsquelle

Amplitude
Gleichspannungsanteil, Offset
Komplexer Innenwiderstand
Generator: Induktivität
Frequenz

MischQuelle.asc

Version 4
SHEET 1 880 680
WIRE 160 32 112 32
WIRE 256 32 240 32
WIRE 352 32 336 32
WIRE 112 64 112 32
WIRE 112 176 112 144
WIRE 112 288 112 256
FLAG 112 288 0
FLAG 352 32 Uout
SYMBOL voltage 112 160 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(0 1 1k)
SYMBOL voltage 112 48 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value 3
SYMBOL res 352 16 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RI
SYMATTR Value 10
SYMBOL ind 144 48 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 5 56 VBottom 2
SYMATTR InstName L1
SYMATTR Value 5m
TEXT 280 288 Left 2 !.tran 4m

Das Schaltbild hat besteht aus einer Gleichspannugsquelle und einer Wechselspannungsquelle.
Der Innenwiderstand kann komplex sein. Hier ist eine Induktivität eines Generators gezeigt.
In SPICE kann man der Wechselspannungsquelle direkt einen Gleichanteil (Offset) hinzufügen.

Wechselspannungsquelle: Frequenzgang

Spannungsbereich
Maximalfrequenz
Kopfhörer, Lautsprecher
Übertragungsfunktion

Frequenzgang

Messgerät: Netzwerkanalysator, Spektrumanalysator Lautsprecherweiche Hochtöner, Tieftöner	Sinuslive 3-Wege-Frequenzweiche CR345

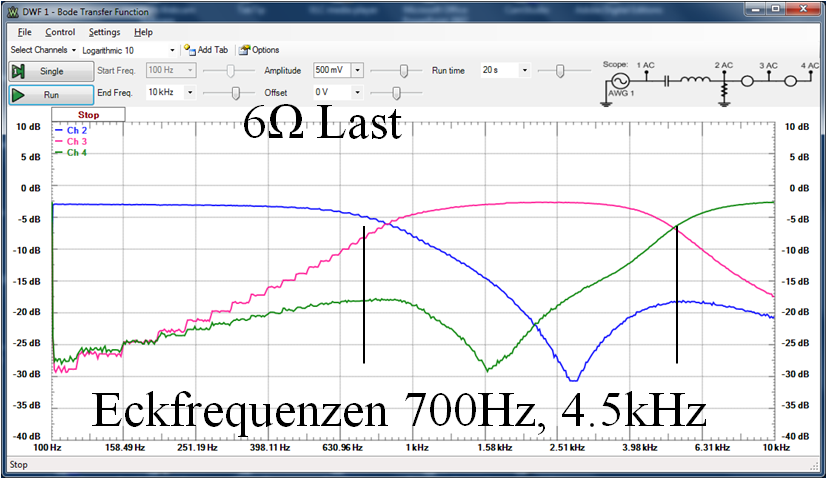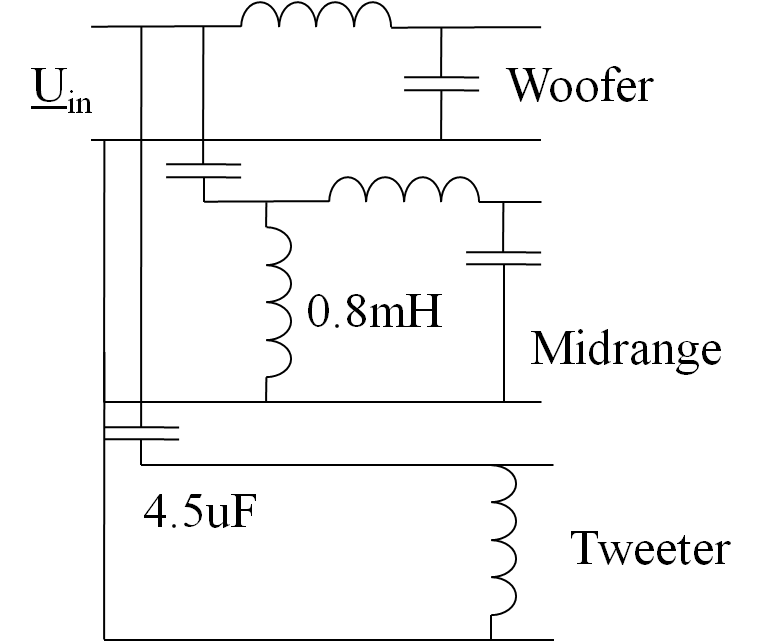Gesteuerte Quelle: 4 Pole

4 Anschlüsse
Eingang: Eingangswiderstand
Ausgang: Quelle, Innenwiderstand, Ausgangswiderstand

Bsp: Spannungsgesteuerte Spannungsquelle

BQuelle.asc

Version 4
SHEET 1 880 680
WIRE 96 96 16 96
WIRE 288 96 224 96
WIRE 400 96 368 96
WIRE 96 128 96 96
WIRE 224 128 224 96
WIRE 96 240 96 208
WIRE 224 240 224 208
FLAG 96 240 0
FLAG 16 96 UE
IOPIN 16 96 In
FLAG 224 240 0
FLAG 400 96 UA
IOPIN 400 96 Out
SYMBOL res 80 112 R0
SYMATTR InstName RE
SYMATTR Value 100k
SYMBOL bv 224 112 R0
SYMATTR InstName B1
SYMATTR Value V=100*V(UE)
SYMBOL res 384 80 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RA
SYMATTR Value 100
TEXT -24 48 Left 2 !VE UE 0 SINE(0 0.1 1k) AC 1
TEXT -40 224 Left 2 !.tran 4m
TEXT 144 -80 Left 2 ;UE
TEXT 392 -80 Left 2 ;UA
TEXT 112 0 Left 2 ;GND
TEXT 392 0 Left 2 ;GND
LINE Normal 224 -80 176 -80
LINE Normal 224 0 176 0
LINE Normal 384 0 336 0
LINE Normal 384 -80 336 -80
LINE Normal 336 -96 224 -96
LINE Normal 336 16 336 -96
LINE Normal 224 16 336 16
LINE Normal 224 -96 224 16
RECTANGLE Normal 336 16 224 -96

Beispiel:
Gleichung:
V = 100 · V(UE)

Die Eingangsspannung wird um den Faktor 100 verstärkt.
Es können beliebige Gleichungen eingegeben werden.

Bsp: Widerstand

Modellierung mit einer Stromquelle mit der Gleichung
I = V(U)/{RX}

Bsp: nichtlineare Gleichung

I=V(UX)/100*V(UX)/100*V(UX)/100

NonLinear.asc

Version 4
SHEET 1 880 680
WIRE 176 80 64 80
WIRE 384 80 176 80
WIRE 176 112 176 80
WIRE 64 160 64 80
WIRE 64 256 64 240
WIRE 176 256 176 192
FLAG 64 256 0
FLAG 176 256 0
FLAG 384 80 UX
SYMBOL bi 176 112 R0
WINDOW 3 10 101 Left 2
SYMATTR InstName B1
SYMATTR Value I=(V(UX)**3)/1000000
SYMBOL voltage 64 144 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value 1
TEXT 38 304 Left 2 !.dc V1 -10 10 0.02

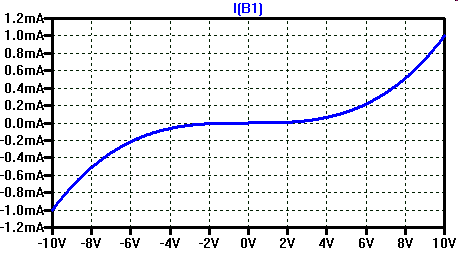Zusammenfassung

Bauelementmodelle werden in der Schaltungssimulation und dem Schaltungsentwurf verwendet.
Bauelementmodelle können anhand von UI Kennlinien (statisch), Signalmessungen und Frequenzgangsmessungen (dynamisch) bestimmt werden.
Geeignete Messbereiche und Messwiderstände müssen gewählt werden.
Ein Bauelementmodell ist nur so genau, wie die verwendeten Elemente
Beim Schaltungsentwurf verwendet man bekannte Bauteilmodelle oder erstellt sich eigene aus Messungen oder dem Datenblatt

Nächstes Mal: 17 Der Operationsverstärker

2020 Elektronik 16 Modelle Prof. Dr. Joerg Vollrath

Elektronik

16 Modelle

Prof. Dr. Jörg Vollrath

Video der 17. Vorlesung 1.12.2020

Video Quellenmessung 2.6.2022

Video Bodediagram RC Messung 2.6.2022

Übersicht

Lernziele

Sie kennen Modelle von Bauelementen

Sie können von einem Bauteil ein Modell erstellen

Lineare Modelle

Widerstandsmessung

UI Kennlinie

Kapazitätsmessung dU/dt

Strommessung

mit Spannungsrampe

Induktivitätsmessung mit Übertragungsfunktion

Laborarbeitsplatz Electronic Explorer

Quellen: DC Gleichspannung

Reale Spannungsquelle

Arbitrary Waveform Generator

Electronic Explorer

Reale Spannungsquelle

Arbitrary Waveform Generator

Electronic Explorer

Die Kennlinien von Quellen

Messung

AC Wechselspannungsquelle

Wechselspannungsquelle: Frequenzgang

Frequenzgang

Gesteuerte Quelle: 4 Pole

Bsp: Spannungsgesteuerte Spannungsquelle

Bsp: Widerstand

Bsp: nichtlineare Gleichung

Zusammenfassung