Elektronik

20 Stabilität des Operationsverstärkers

Prof. Dr. Jörg Vollrath

19 Anwendung Operationsverstärker

Video der 20. Vorlesung 15.12.2020

Länge: 01:01:43

0:0:9 Umformung der Übertragungsfunktion

0:3:40 Instabilität des Verstärkers

0:9:32 Maximale Verstärkung und Grenzfrequenz ablesen

0:10:59 Ergebnisse

0:13:49 20dB/40dB/60dB pro Dekade

0:16:1 Instabilität im Zeitbereich LTSPICE

0:19:49 Modell der Gegenkopplung

0:20:39 Ringoszillator

0:22:49 Stabiler Arbeitspunkt 0V

0:27:18 Schmitt Trigger

0:33:14 Rechnung

0:38:21 Hysterese

0:40:37 Relaxationsoszillator

0:44:14 Integrierer und Schmitt Trigger

0:50:44 T1= UH C1 R1 /Uamax

0:52:22 LTSPICE

0:57:43 Frequenzberechnung

0:59:40 Schaltungsaufbau

1:4:9 Trigger und stehendes Bild

1:7:44 Unterschiede Rechnung, Simulation, messung

Rückblick und Heute

Gegenkopplung, Instabilität
Mitkopplung
Schmitt-Trigger, Hysterese
Funktionsgenerator

Reinhold 11.5, 12.4,

Bei Schaltungen mit Rückkopplungen kann es eine stabile Gegenkopplung geben, eine Mitkopplung oder eine Oszillation.
Praktisch kann man sich neben dem rückgekoppelten Operationsverstärkers (stabile Rückkopplung) die Beispiele Latch (Mitkopplung) und des Ringoszillators anschauen.
Mathematisch werden die Pole und Nullstellen der Übertragungsfunktion untersucht.
Praktisch kann man die Phasendifferenz und Verstärkung zwischen rückgekoppeltem Signal und Eingangssignal untersuchen.
Für ein stabiles rückgekoppeltes System muss die Phasenreserve größer als 60° sein. Die Phasenreserve ist die minimale Phasendifferenz zwischen Ausgangssignal und Eingangssignal unterhalb der Transitfrequenz.
Diese Forderung nennt man Nyquistkriterium.

Modell der Gegenkopplung

Übertragungsfaktor (open loop gain): $\underline{V}$
Schleifenverstärkung:

$\underline{K} \cdot \underline{V}$

Rückkopplungsgrad:

$\underline{g} = 1 - \underline{K} \cdot \underline{V}$

Stabile Rückkopplung
(Gegenkopplung):
$|\underline{g}| \gt 1$
Keine Signalrückführung
$|\underline{g}| = 1$
Instabile Rückkopplung (Mitkopplung)
$|\underline{g}| < 1$
Selbsterregung (Oszillator)
$|\underline{g}| = 0$
K · V = 1
φ_S = n · 360°

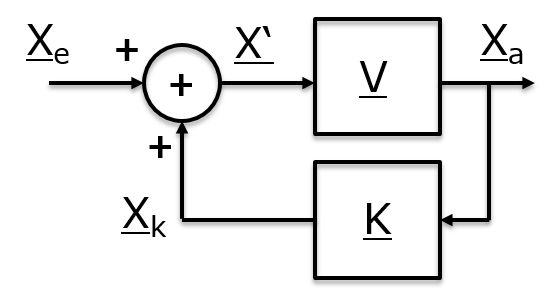$\underline{X}_a = \underline{V} \left( \underline{X}_e + \underline{K} \cdot \underline{X}_a \right)$

$\underline{Vg} = \frac{\underline{X}_a}{\underline{X}_e} = \frac{\underline{V}}{1 - \underline{K} \cdot \underline{V}} = \frac{\underline{V}}{\underline{g}}$

Für sehr grosses V:

$\underline{Vg} = \frac{1}{\frac{1}{\underline{V}} - \underline{K} } \approx \frac{1}{\underline{K}}$

Nyquist Kriterium

Ein System wird instabil wenn bei einer Phasendrehung innerhalb der Gegenkopplungsschleife ein vielfaches von 360° beträgt und die Schleifenverstärkung für diese Frequenz größer gleich 1 ist.

Instabilität des Verstärkers

Im Schaltbild wird ein Operationsverstärker ohne Beschaltung und in nichtinvertierender Konfiguration und die zugehörigen Freqenzgänge gezeigt.

OpAmpin4.asc

Version 4
SHEET 1 1064 680
WIRE 160 128 160 80
WIRE 432 128 432 80
WIRE 144 144 96 144
WIRE 416 144 368 144
WIRE 256 160 208 160
WIRE 272 160 256 160
WIRE 544 160 480 160
WIRE 144 176 112 176
WIRE 256 176 256 160
WIRE 416 176 368 176
WIRE 368 192 368 176
WIRE 160 224 160 192
WIRE 432 224 432 192
WIRE 112 272 112 176
WIRE 256 272 256 256
WIRE 256 272 112 272
WIRE 256 288 256 272
WIRE 256 384 256 368
FLAG 160 80 Vp
FLAG 160 224 Vn
FLAG 96 144 Ve
FLAG 272 160 Va
FLAG 256 384 0
FLAG 432 80 Vp
FLAG 432 224 Vn
FLAG 368 144 Ve1
FLAG 544 160 Va1
FLAG 368 192 0
SYMBOL res 272 384 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL res 272 272 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName R2
SYMATTR Value {RX}
SYMBOL OpAmpModel2 176 160 M180
SYMATTR InstName X1
SYMATTR SpiceLine VDOL=40k GBW2=1E6 GBW=5E8
SYMBOL OpAmpModel2 448 160 M180
SYMATTR InstName X2
SYMATTR SpiceLine VDOL=40k GBW2=1E6 GBW=5E8
TEXT 304 272 Left 2 !Vp Vp 0 15\nVn Vn 0 -15
TEXT 296 360 Left 2 !;tran 0 0.2m 0 1u
TEXT 304 328 Left 2 !.ac dec 10 1 1G
TEXT 48 424 Left 2 !V1 Ve 0 PULSE(0 2m 0.01m 1n 1n 0.099m 0.2m) AC 1\nV2 Ve1 0 PULSE(0 25u 0.01m 1n 1n 0.099m 0.2m) AC 1
TEXT 296 392 Left 2 !.step param RX 500k 5k -495k

Der Operationsverstärker besitzt das Verhalten eines Tiefpasses 3. Ordnung.
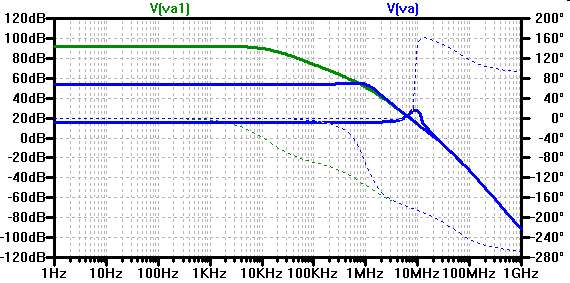Bestimmen Sie aus dem dargestellten Frequenzgang die maximale Verstärkungen mit und ohne Beschaltung und die Grenzfrequenzen des Operationsverstärkers.
An welcher Stelle ist |g| = 0 bzw. K · V = 1.
Wie gross ist dort die Phase?

Die Grenzfrequenzen liest man an den Stellen ab, an denen sich die Steigung ändert oder bei der sich die Phase um 45° geändert hat.
Der Pegel des Eingangssignals ist 0 dB (LTSPICE: AC 1).

Va1:
Maximale Verstärkung: 92 dB entsprechen: v_U = 4000.

Die gestrichelte Linie (grün) wird der Phase zugeordnet:
f_{1 3dB} (89 dB, -45°) = 10 kHz
f_{2 3dB} (-135°) = 1 MHz
f_{3 3dB} (-225°) = 50 MHz

Das Maß 55 dB entspricht der Verstärkung: v_U = 600.

Die grüne Kurve zeigt die Verstärkung V.
Die blaue Kurve zeigt die Gegenkopplung 1/K.
Bei ca. 1 MHz sind beide Kurven identisch: V · K = 1.
Die Phase (grüne Kurve) liegt bei ca -100°.
Die Rückkoppelung über den negativen Eingang addiert eine Phasendrehung von 180°.

Hier wird ein Verstärker 3. Ordnung gezeigt, um sicher eine Phasendrehung von mehr als 180° zu errreichen.
Für einen kleinen R2 = 5 k wird K gross genug, damit der Verstärker schwingt.
Das Maß ist 15.8 dB entsprechend einer Spannungsverstärkung von 6.
Die blau gestrichelte Kurve zeigt bei 10 MHz eine 180° Phasendrehung.
Die Schwingung in der zeitlichen (.tran) Simulation hat eine Frequenz von 10MHz.

Das folgende Bild zeigt ein einfaches Model für einen Operationsverstärker 3.Ordnung.
Die dritte Ordnung setzt sich aus R1, C1; R2, C2; R3, C3 zusammen.

OpAmpModel2.asc

Version 4
SHEET 1 1080 680
WIRE 128 -128 128 -160
WIRE 208 -128 208 -160
WIRE 704 -80 592 -80
WIRE 784 -80 704 -80
WIRE 800 -80 784 -80
WIRE 592 -48 592 -80
WIRE 704 -48 704 -80
WIRE 784 -32 784 -80
WIRE 128 -16 128 -48
WIRE 208 -16 208 -48
WIRE 592 64 592 32
WIRE 640 64 592 64
WIRE 704 64 704 32
WIRE 704 64 640 64
WIRE 784 64 784 32
WIRE 784 64 704 64
WIRE 128 80 128 48
WIRE 128 80 96 80
WIRE 208 80 208 48
WIRE 208 80 128 80
WIRE 288 80 208 80
WIRE 368 80 288 80
WIRE 512 80 448 80
WIRE 544 80 512 80
WIRE 640 80 640 64
WIRE 96 112 96 80
WIRE 208 112 208 80
WIRE 48 128 -16 128
WIRE 288 128 288 80
WIRE 512 128 512 80
WIRE 48 176 -16 176
WIRE 96 224 96 192
WIRE 144 224 96 224
WIRE 208 224 208 192
WIRE 208 224 144 224
WIRE 288 224 288 192
WIRE 288 224 208 224
WIRE 512 224 512 192
WIRE 512 224 288 224
WIRE 144 240 144 224
FLAG 144 240 0
FLAG -16 128 InP
IOPIN -16 128 In
FLAG -16 176 InM
IOPIN -16 176 In
FLAG 800 -80 Out
IOPIN 800 -80 Out
FLAG 128 -160 VDD
FLAG 208 -160 VSS
FLAG 512 80 Vo1
FLAG 640 80 0
SYMBOL g 96 96 R0
SYMATTR InstName G1
SYMATTR Value {VDol/R}
SYMBOL res 192 96 R0
SYMATTR InstName R1
SYMATTR Value {R}
SYMBOL cap 272 128 R0
SYMATTR InstName C1
SYMATTR Value {VDol/GBW/Pi2}
SYMBOL diode 192 -16 R0
SYMATTR InstName D1
SYMATTR Value LIMITV
SYMBOL diode 144 48 R180
WINDOW 0 24 64 Left 2
WINDOW 3 26 3 Left 2
SYMATTR InstName D2
SYMATTR Value LIMITV
SYMBOL voltage 128 -144 R0
SYMATTR InstName V3
SYMATTR Value 2
SYMBOL voltage 208 -144 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V4
SYMATTR Value -2
SYMBOL cap 496 128 R0
SYMATTR InstName C2
SYMATTR Value {1/GBW2/RS/Pi2}
SYMBOL res 464 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value {RS}
SYMBOL res 688 -64 R0
SYMATTR InstName R3
SYMATTR Value {R3}
SYMBOL cap 768 -32 R0
SYMATTR InstName C3
SYMATTR Value {1/GBW3/Pi2}
SYMBOL bi 592 32 R180
WINDOW 0 24 80 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName B1
SYMATTR Value I=V(Vo1)
TEXT -224 -24 Left 2 !VSS VSS 0 DC -5\nVDD VDD 0 DC 5
TEXT 280 -32 Left 2 !.param VDol=1000k
TEXT 272 0 Left 2 !.param GBW2 1E6
TEXT 88 280 Left 2 !.model LIMITV D(Is=2.52n Rs=.00000001 N=1.752 )
TEXT 280 -64 Left 2 !.param R 1
TEXT -224 -144 Left 2 !.param Pi2 6.2831530717959
TEXT 288 -96 Left 2 !.param RS 25
TEXT 280 -128 Left 2 !.param GBW 1E6
TEXT 592 -168 Left 2 !.param R3 1
TEXT 584 -136 Left 2 !.param GBW3 5E7

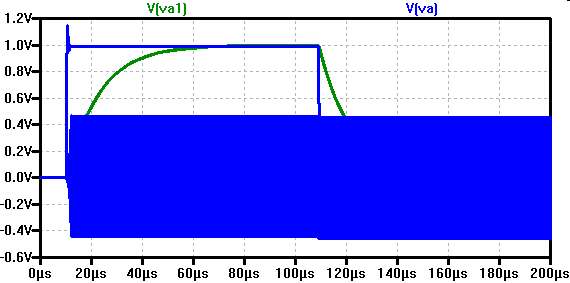
Instabilität des Verstärkers

Sprungantwort eines gegengekoppelten Verstärkers.
K = 1/500
K = 1/5

Für ein schnelles und sicheres Einschwingen benötigt ein Verstärker eine Phasenreserve von mindestens 60°.

Ringoszillator

Man kann einen Ringoszillator mit einer ungeraden Anzahl von Verstärkern bauen.

RingOsciOpAmp.asc

Version 4
SHEET 1 888 680
WIRE 160 128 160 80
WIRE 304 128 304 80
WIRE 448 128 448 80
WIRE 48 144 32 144
WIRE 128 144 48 144
WIRE 272 144 224 144
WIRE 416 144 368 144
WIRE 224 160 224 144
WIRE 224 160 192 160
WIRE 368 160 368 144
WIRE 368 160 336 160
WIRE 512 160 480 160
WIRE 128 176 96 176
WIRE 272 176 240 176
WIRE 416 176 384 176
WIRE 96 208 96 176
WIRE 240 208 240 176
WIRE 384 208 384 176
WIRE 160 224 160 192
WIRE 304 224 304 192
WIRE 448 224 448 192
WIRE 32 288 32 144
WIRE 512 288 512 160
WIRE 512 288 32 288
FLAG 160 80 Vp
FLAG 160 224 Vn
FLAG 96 208 0
FLAG 304 80 Vp
FLAG 304 224 Vn
FLAG 240 208 0
FLAG 448 80 Vp
FLAG 448 224 Vn
FLAG 384 208 0
FLAG 48 144 V0
FLAG 224 144 V1
FLAG 368 144 V2
SYMBOL OpAmpX 160 160 R0
SYMATTR InstName X1
SYMBOL OpAmpX 304 160 R0
SYMATTR InstName X2
SYMBOL OpAmpX 448 160 R0
SYMATTR InstName X3
TEXT 24 56 Left 2 !Vp Vp 0 15\nVn Vn 0 -15
TEXT 264 312 Left 2 !.tran 0 4u 0
TEXT 32 344 Left 2 !;dc V1 15 -15 0.1
TEXT 32 312 Left 2 !.global VP VN
TEXT 288 344 Left 2 !.ic v(v0)=2

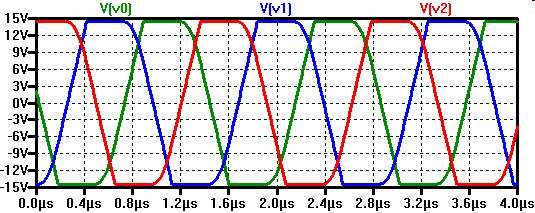
Für die Simulation benötigt man eine Anfangsbedingung (.ic initial condition) um eine Spannung zu setzen und die Schwingung zu starten.
Es gibt einen theoretischen stabilen Zustand, wenn alle Spannungen V0, V1,V2 auf 0V liegen.
In der Realität sollte dieser Zustand nicht auftreten, da es Störsignale und Unterschiede in realen Operationsverstärkern gibt.
Der Schaltungsentwickler sollte nicht nur eine stabilen Zustand (ein/aus) sondern auch das Einschalten und ausschalten einer Schaltung untersuchen.

Schmitt Trigger

Ein Schwellwertschalter mit Hysterese

SchmittL.asc

Version 4
SHEET 1 888 680
WIRE 96 128 64 128
WIRE 160 128 160 112
WIRE 64 144 64 128
WIRE 96 144 96 128
WIRE 128 144 96 144
WIRE 288 160 192 160
WIRE 320 160 288 160
WIRE -32 176 -64 176
WIRE 96 176 48 176
WIRE 128 176 96 176
WIRE 160 208 160 192
WIRE 96 304 96 176
WIRE 128 304 96 304
WIRE 288 304 288 160
WIRE 288 304 208 304
FLAG 64 144 0
FLAG 320 160 Va
IOPIN 320 160 Out
FLAG -64 176 Ve
IOPIN -64 176 In
FLAG 96 176 Vx
FLAG 160 112 VP
FLAG 160 208 VN
SYMBOL res 64 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL res 224 288 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL OpAmpX 160 160 R0
SYMATTR InstName X1
TEXT -88 96 Left 2 !.tran 0 200m 0
TEXT 128 32 Left 2 !;dc V1 15 -15 0.1
TEXT -120 368 Left 2 !V1 Ve 0 PULSE(-5 5 0 100m 100m 0 200m)
TEXT 208 88 Left 2 !.global VP VN
TEXT -88 32 Left 2 !VP VP 0 DC 15\nVN VN 0 DC -15

Achtung: Der Anschluß der Eingangsspannung an den Operationsverstärker erfolgt am positiven Eingang des Operationsverstärkers.

$U_H = U_{eE} - U_{eA}$
Berechnung der Umschaltschwellen

Erster Fall:

$U_a = U_{amin}$ ;

$U_e < U_{eE}$
Für den Umschaltpunkt muss gelten:

$I(U_x = 0) = \frac{U_{eE}}{R1} = - \frac{U_{amin}}{R_2}$

$U_{eE} = - U_{amin} \frac{R_1}{R_2}$
Symmetrie:

$U_{eA} = - U_{amax} \frac{R_1}{R_2}$
Hysterese:

$U_H = U_{eE} - U_{eA} = \left( U_{amax} - U_{amin} \right) \frac{R_1}{R_2}$

Reale Signale haben immer Störungen.
Kleine Wechselspannungen sind dem idealen Signal überlagert.
Wenn sich das Eingangssignal ändert kann es an der Umschaltschwelle durch die Störsignale zum mehrmaligen Umschalten oder Prellen führen.
Um das zu verhindern kann man einen Tiefpass oder eine Hysterese einsetzen.

Schmitt Trigger in LTSPICE

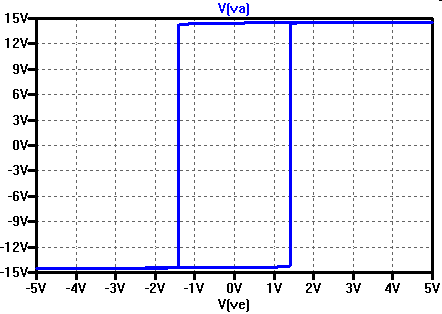
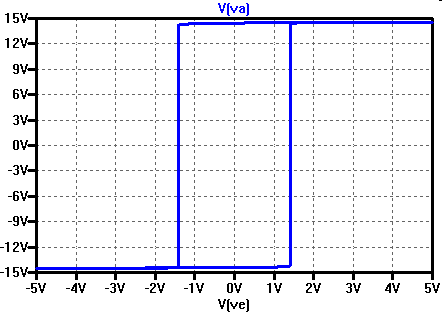
Realer Operationsverstärker

$U_{amax}, U_{amin}$
LTSPICE: DC Simulation zeigt keine Hysterese
Transiente Simulation
LTSPICE Mausklick auf x - Achse: V(ve)
Hysterese:

$U_H = \left( U_{amax} - U_{amin} \right) \frac{R_1}{R_2}$

$U_H = \left( 14 V - (- 14 V) \right) \frac{1 k\Omega}{10k\Omega} = 2.8 V$
Oszilloskopmessung: x-y Betrieb

SchmittL1.asc

Version 4
SHEET 1 888 680
WIRE 96 128 64 128
WIRE 160 128 160 80
WIRE 64 144 64 128
WIRE 96 144 96 128
WIRE 128 144 96 144
WIRE 288 160 192 160
WIRE 320 160 288 160
WIRE -32 176 -64 176
WIRE 96 176 48 176
WIRE 128 176 96 176
WIRE 160 224 160 192
WIRE 96 304 96 176
WIRE 128 304 96 304
WIRE 288 304 288 160
WIRE 288 304 208 304
FLAG 160 80 Vp
FLAG 160 224 Vn
FLAG 64 144 0
FLAG 320 160 Va
IOPIN 320 160 Out
FLAG -64 176 Ve
IOPIN -64 176 In
FLAG 96 176 Vx
SYMBOL res 64 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL res 224 288 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL OpAmpX 160 160 R0
SYMATTR InstName X1
TEXT -88 32 Left 2 !Vp Vp 0 15\nVn Vn 0 -15
TEXT -88 96 Left 2 !.tran 0 200m 0
TEXT 128 32 Left 2 !;dc V1 15 -15 0.1
TEXT -120 368 Left 2 !V1 Ve 0 PULSE(-5 5 0 100m 100m 0 200m)
TEXT 200 112 Left 2 !.global VP VN

Relaxationsoszillator

Rückgekoppelte Schaltung
Ladevorgang am Kondensator
Integrator, Schmitt Trigger

Relax.asc

Version 4
SHEET 1 888 680
WIRE 288 -32 -320 -32
WIRE -208 32 -224 32
WIRE -96 32 -144 32
WIRE 96 128 64 128
WIRE 160 128 160 80
WIRE -176 144 -176 112
WIRE 64 144 64 128
WIRE 96 144 96 128
WIRE 128 144 96 144
WIRE -320 160 -320 -32
WIRE -224 160 -224 32
WIRE -224 160 -240 160
WIRE -208 160 -224 160
WIRE 288 160 288 -32
WIRE 288 160 192 160
WIRE -96 176 -96 32
WIRE -96 176 -144 176
WIRE -48 176 -96 176
WIRE -32 176 -48 176
WIRE 96 176 48 176
WIRE 128 176 96 176
WIRE -208 192 -224 192
WIRE 160 224 160 192
WIRE -224 240 -224 192
WIRE -176 240 -176 208
WIRE 96 320 96 176
WIRE 128 320 96 320
WIRE 288 320 288 160
WIRE 288 320 208 320
FLAG 160 80 Vp
FLAG 160 224 Vn
FLAG 64 144 0
FLAG 288 160 V2
FLAG -176 112 Vp
FLAG -176 240 Vn
FLAG -224 240 0
FLAG -48 176 V1
SYMBOL res 64 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 1k
SYMBOL res 224 304 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R3
SYMATTR Value 10k
SYMBOL cap -144 16 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C1
SYMATTR Value 10�
SYMBOL res -224 144 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL OpAmpX -176 176 R0
SYMATTR InstName X1
SYMBOL OpAmpX 160 160 R0
SYMATTR InstName X2
TEXT -40 -8 Left 2 !Vp Vp 0 15\nVn Vn 0 -15
TEXT -56 56 Left 2 !.tran 0 20m 0
TEXT -48 256 Left 2 !;.ic V(v1)=1
TEXT -64 88 Left 2 !.global VP VN

Die gewünschte Spannnung würde man mit einer Operatiosnverstärkerschaltung nach aussen bringen.
Die Operationsverstärkerschaltung stellt sicher, dass der Generator nicht belastet und der gewünschte Ausgangspegel und Ausgangswiderstand eingestellt wird.

Relaxationsoszillator Rechnung

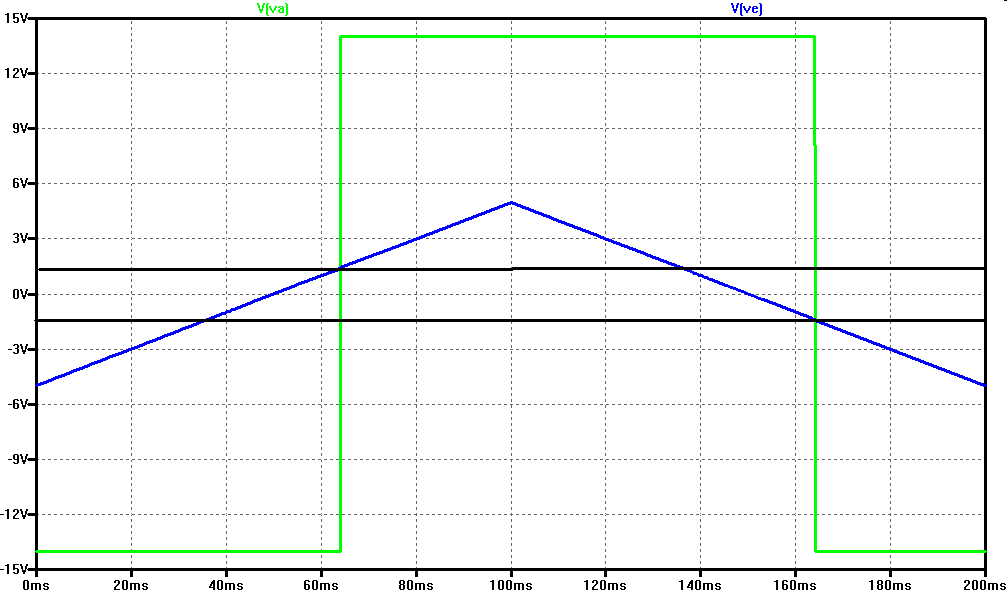
Die Spannungsverläufe

$U_1(t)$ und

$U_2(t)$ des Funktionsgenerators, sowie deren Frequenz sind zu bestimmen.

(1) Identifizierung der Blöcke
Integrator, Schmitt-Trigger
(2) Bestimmung der Parameter

$0 \leq t \leq T_1:$

$U_2(t) = U_{amax}, U_1(0) = U_{eE}$

$U_1(t) = - \frac{1}{C_1 R_1} \int_{0}^{t} U_{amax} dt + U_{eE}$

$U_1(T_1) = - \frac{U_{amax} \cdot T_1}{C_1 R_1} + U_{eE} = U_{eA}$

$T_1 = \left( U_{eE} - U_{eA} \right) \frac{C_1 \cdot R_1}{U_{amax}}$

$U_{amax} = - U_{amin} = U_B$

$U_{eE} = - U_{eA} = \frac{R_2}{R_3} U_B$

$f = \frac{1}{2 \cdot T_1} = \frac{U_{amax}}{2 \cdot C_1 R_1 \left( U_{eE} - U_{eA} \right)}$

$f = \frac{U_B \cdot R_3}{2 \cdot C_1 R_1 R_2 \left( U_{B} + U_{B} \right)}$

$f = \frac{R_3}{4 \cdot C_1 \cdot R_1 \cdot R_2} =\frac{10 k\Omega}{4 \cdot 10 \mu F \cdot 1 k\Omega \cdot 1 k\Omega}$

$f = \frac{1}{4 ms} = 250 Hz$

Relax.asc

Relaxationsoszillator Simulation

Es gibt 2 Arbeitspunkte: 0 V und oszillierend.
Man muss auch immer das Einschalten und Ausschalten betrachten.
Setzen einer Spannung mit .ic (initial condition)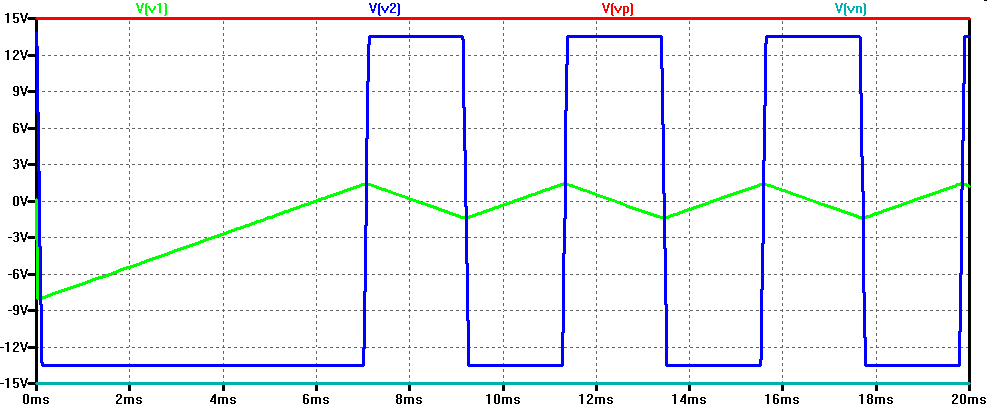

Relax.asc

Nachdenken über die Lösung

Zerlegung in Blöcke
Einzelblockberechnung
Zeichnung
Anfangsbedingung
Verifikation mit der Simulation
Aufbau und Messung der Schaltung

Funktionsgenerator
Rechtecksignal
Dreiecksignal

Relaxationsoszillator realer Versuchsaufbau

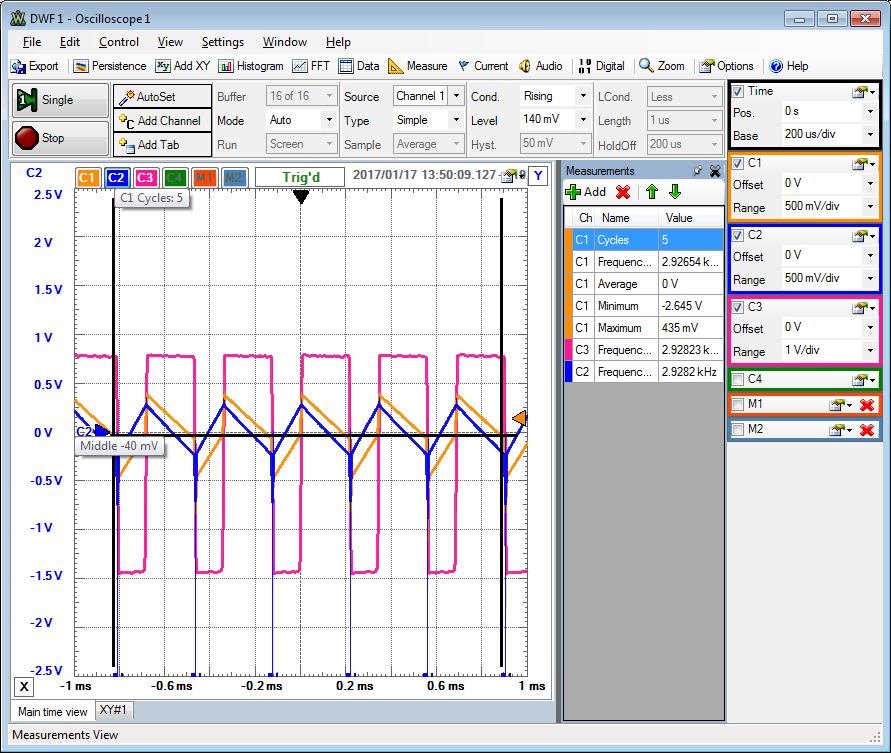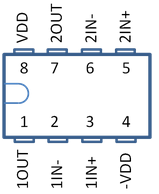
VP+ = 3 V
VP- = -3 V
OSC1: positiver Eingang des Operationsverstärkers des Schmitt-Triggers.
OSC2: Ausgang Integrator, Eingang Schmitt Trigger
OSC3: Ausgang des Schmitt-Triggers,
Maximale positive Spannung: 1.5V
Maximale negative Spannung: -2.9V
f_osc = 2.9kHz
C = 0.68 µF
Op1: Integrator
Op2: Schmitt Trigger
Widerstände: 100Ω, 1kΩ, 1kΩ, 10kΩ, 100kΩ
2. Widerstand Eingang Integrator
3.Widerstand Input Schmitt Trigger

Nächstes Mal:

21 Uebung

2020 10 09 20 Stabilität des Operationsverstärkers Elektronik Prof. Dr. Joerg Vollrath

Elektronik

20 Stabilität des Operationsverstärkers

Prof. Dr. Jörg Vollrath

Video der 20. Vorlesung 15.12.2020

Rückblick und Heute

Modell der Gegenkopplung

Nyquist Kriterium

Instabilität des Verstärkers

Instabilität des Verstärkers

Ringoszillator

Schmitt Trigger

Schmitt Trigger in LTSPICE

Relaxationsoszillator

Relaxationsoszillator Rechnung

Relaxationsoszillator Simulation

Nachdenken über die Lösung

Relaxationsoszillator realer Versuchsaufbau

Nächstes Mal: