Elektronik

22 Diode

Prof. Dr. Jörg Vollrath

21 Übung

Video der 22. Vorlesung 22.12.2020

Länge: 00:00:00

0:1:0 Diodenübersicht

0:2:46 Handtaschenlampe

0:5:50 Strom-Spannungskennlinie und Gleichung der Diode

0:13:50 Excel Diodenkennlinien

0:19:28 Serienwiderstand

0:25:8 SPICE Diodenmodell

0:30:8 LED blinkt im praktischen Aufbau

0:34:54 Bestimmung der Parameter, Strommessung mit Widerstand

0:36:33 Dreieckspannung

0:38:8 Oszilloskopbild

0:40:25 xy-Darstellung

0:43:18 Leuchtdiode als Beispiel

0:48:46 Strommesswiderstände

0:51:18 Diodenmesswerte zur Bestimmung von Diodenparametern

0:54:23 Arbeitsbereich und Gleichung

0:56:18 Sperrstrom und Sättigungsstrom

0:59:18 Exponentialbereich Berechnung von n

1:2:43 Berechnung Mathnotepad

1:4:14 Widerstandsbereich

1:5:44 2 Werte aus dem Exponentialbereich zur Bestimmung n, Is

1:11:54 Diodenschaltsymbole: Shottky, Zener, LED

1:13:18 Logarithmische Kennlinien verschiedener Dioden

1:16:56 Lineare Kennlinien und Durchbruch

Heute

Dioden Schaltsymbol und Ausführung
Kennlinie
Diodenparameter
Bestimmung der Diodenparameter
Frequenzverhalten
Gleichrichter
Spannungsregler
Spannungsverdopplung

Praxisbeispiel: Dioden

Taschenlampe

2 Dioden
Gleichrichtung
Spannungsverdopplung
Trennung

3 Leuchtdioden LED
Lichterzeugung

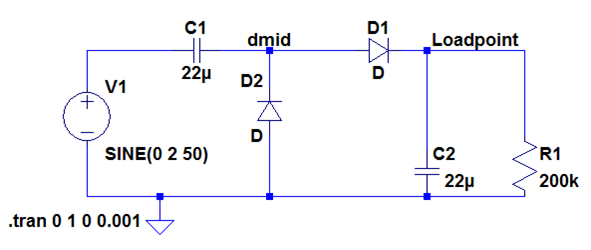Quelle: Joerg Vollrath

Strom-Spannungskennlinie der Diode

Diode_Symbol.asc

Version 4
SHEET 1 880 680
WIRE -32 48 -144 48
WIRE 144 48 32 48
SYMBOL diode 32 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D1
SYMATTR Value ""
TEXT 64 96 Left 2 !Anode
TEXT -144 96 Left 2 !Kathode
TEXT -16 -40 Left 2 ;U
TEXT -72 24 Left 2 ;I
LINE Normal -112 -16 -96 0
LINE Normal -96 -32 -112 -16
LINE Normal 96 -16 -112 -16
LINE Normal -96 48 -80 32
LINE Normal -80 64 -96 48

Vorwärtsbetrieb
$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

$\frac{U}{nU_T} \gt 1$

$I_D = I_S \left( e^{\frac{U}{nU_T}} \right)$

Temperaturspannung: $U_{T} = \frac{kT}{q} = 0.025 V$
für T=300K, Raumtemperatur
q = e = 1.6 · 10^-19 C
Elementarladung
k = 1.38 · 10^-23 J/K
Boltzmannkonstante
$10^{-18}A \lt I_S \lt 10^{-9}$
Schleusenspannung oder Flussspannung
Darstellungen

Achsen linear

Strombereich für positive und negative Werte unterschiedlich

Stromachse logarithmisch

Stromwerte absolut
Kein Logarithmus einer negativen Zahl möglich
Ablesen des Exponenten

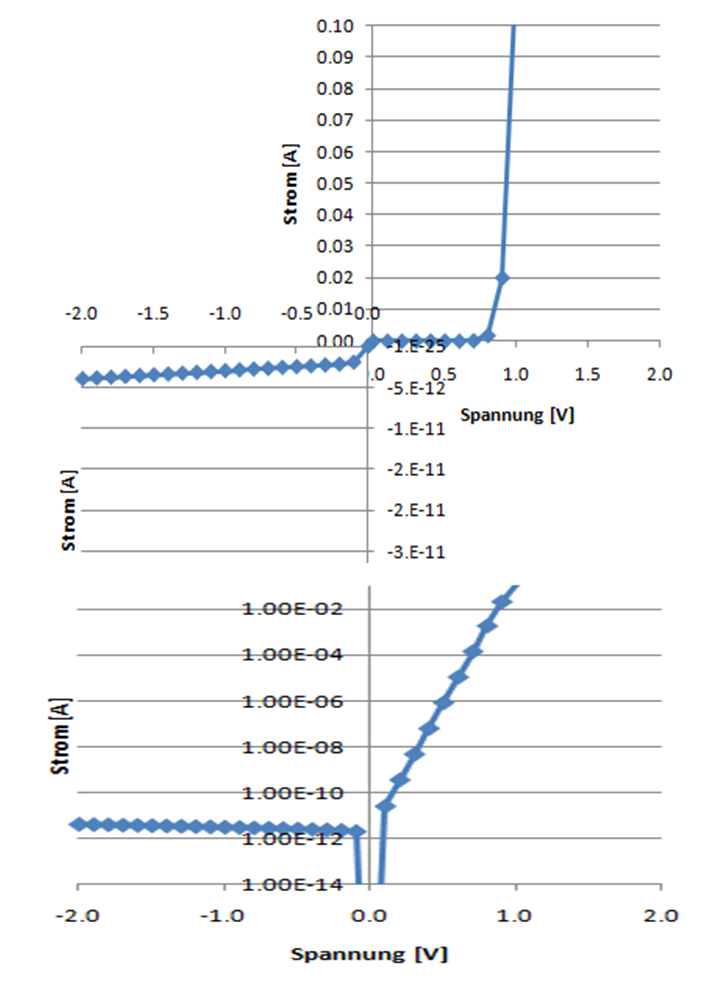Quelle: Vollrath

SPICE Diodenmodell

.model 1N914 D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=20n Iave=200m Vpk=75 mfg=Motorola type=silicon)

DC Simulation

Is Saturation current
Rs Series Resistance
N Emission Coefficient
BV, IBV Breakdown voltage

AC, Transient Simulation

Cjo Zero bias junction capacitance
M Grading coefficient
Tt Transit time

Iave Current rating
Vpk Peak voltage rating
Type LED, zener, silicon, Shottky
Mfg Hersteller

$I_D = I_S\left( e^{\frac{q (U - I_D * R_S )}{nkT}}-1\right)$

DiodeModel.asc

Version 4
SHEET 1 880 680
WIRE 16 32 16 0
WIRE 144 112 16 112
WIRE 16 128 16 112
WIRE 144 144 144 112
WIRE 16 240 16 208
WIRE 144 240 144 208
WIRE 144 240 16 240
WIRE 16 272 16 240
SYMBOL res 0 16 R0
SYMATTR InstName RS
SYMATTR Value ""
SYMBOL current 16 128 R0
SYMATTR InstName BI
SYMATTR Value ID=F(VD)
SYMBOL cap 128 144 R0
WINDOW 0 -68 -52 Left 2
SYMATTR InstName C=Cj+CD
SYMATTR Value ""

Quelle: Vollrath

Bestimmung der Parameter der Diodengleichung

Es sollen von einer Diode Is, n und Rs bestimmt werden.

3 Unbekannte, 3 Gleichungen

Der Strom wird mit einem Widerstand gemessen.
Welche Widerstandswerte werden benötigt?

Das Spannungsmessgerät hat eine begrenzte Auflösung: 20mV
Die maximale Spannung der Spannungsversorgung beträgt 10V

$I = \frac{U}{R} = \frac{UOSC2 - UOSC1}{R1}$

R [ $\Omega$ ]	I_min	I_max
10
100
1k
1M

R [ $\Omega$ ]	I_min	I_max
10	2 mA	1 A
100	0.2 mA	100 mA
1k	20 $\mu$ A	10 mA
1M	20 nA	10 $\mu$ A

DiodeR1.asc

Version 4
SHEET 1 1308 680
WIRE 176 80 80 80
WIRE 288 80 256 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 OSC1
FLAG 80 80 OSC2
SYMBOL voltage 80 112 R0
SYMATTR InstName V1
SYMATTR Value 1
SYMBOL res 272 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1
SYMATTR Value Dx
TEXT 64 296 Left 2 !.model Dx D(Is=10f Rs=0.0\n+ N=1.0 Cjo=0 M=0.5  tt=0  \n+Iave=200m Vpk=75 mfg=Motorola type=silicon)
TEXT 308 228 Left 2 !.dc V1 -1 1 0.01

1M

$\Omega$ ist der Eingangswiderstand des Multimeters/Oszilloskops.

Beispiel: Diodenmessung

An einer idealen Diode mit einem Serienwiderstand RS werden folgende Messungen gemacht.

In welchen Arbeitsbereichen befindet sich die Diode bei den Messungen 1..4?
Bestimmen Sie näherungsweise Is, n und den Serienwiderstand RS. (UT=0.025V)

Messung	1	2	3	4
V_Diode	-2 V	0.5 V	1.4 V	1.6 V
I_Diode	-0.3 nA	11 uA	400 mA	600 mA
Arbeitsbereich

Messung 1:

$I_S = 0.3 nA$ Sättigungsstrom, Sperrstrom
Messung 2:

$I = I_S \left( e^{\frac{U}{n U_T}} \right)$

$n = \frac{U}{ U_T ln \left( \frac{I}{I_S} +1 \right)} = \frac{0.5 V}{ 0.025 V ln \left( \frac{11 \mu A}{0.3 nA} +1 \right)} = 1.9$
Messung 3 und 4:

$U_{Diode3} = n U_T ln \left( \frac{I}{I_S} + 1 \right)$

$= 1.9 \cdot 0.025 V ln \left( \frac{0.4}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_3 - U_{Diode3}}{I_3} = 1 \Omega$

$U_{Diode4} = 1.9 \cdot 0.025 V ln \left( \frac{0.6}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_4 - U_{Diode4}}{I_4} = 0.97 \Omega$

$R_S = \frac{ \Delta U}{ \Delta I} = \frac{U_4 - U_3}{I_4 - I_3} = \frac{0.2 V}{200 mA} = 1 \Omega$

Diodenkennlinie

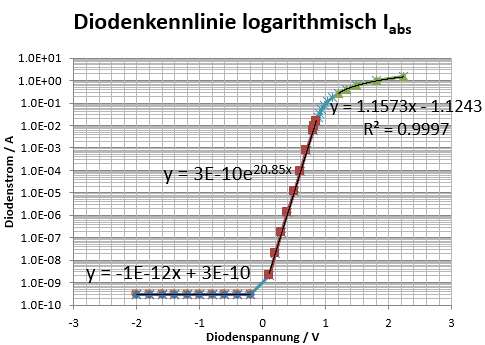
In der logarithmischen Dartsellung sieht man 3 Bereiche.
Links den Sperrbreich der Strom ist näherungsweise konstant: I = I_s
In der Mitte der exponentielle Anstieg:

$I = I_S e^{\frac{U}{n U_T}}$
Rechts der Widerstandsbereich: dI = dU/R

Entsprechende Regressionsgleichungen (Trendlinien) sind im Graphen dargestellt.

x ist dabei die Diodenspannung, y ist der Diodenstrom.

Diodensymbole (LTSPICE) und Gleichung

Vorwärtsbetrieb

$I_D = I_S \left( e^{\frac{q U}{n k T}} - 1 \right)$
Durchbruch

$U_D < BV$

$I_D = - I_S \left( e^{- \frac{q (U+BV)}{n k T}} - 1 + \frac{q BV}{k T} \right)$

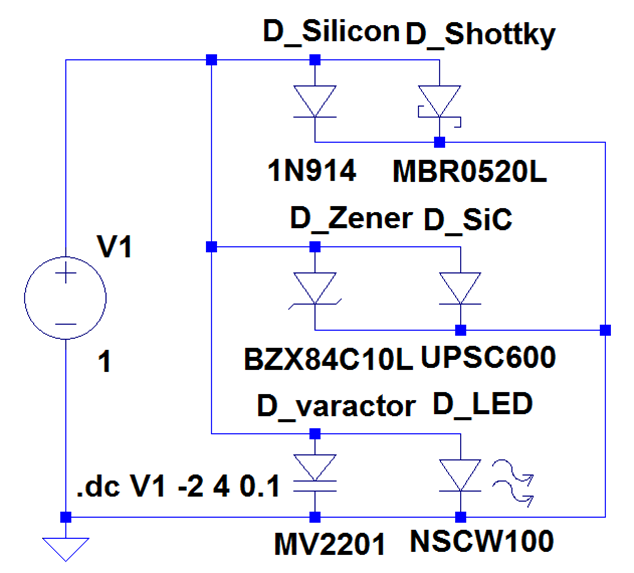Quelle: Vollrath

Dioden_arten_01.asc

Version 4
SHEET 1 880 680
WIRE -288 -160 -336 -160
WIRE -144 -160 -288 -160
WIRE -288 -128 -288 -160
WIRE -144 -128 -144 -160
WIRE -288 -32 -288 -64
WIRE -144 -32 -144 -64
WIRE -288 16 -320 16
WIRE -128 16 -288 16
WIRE -288 32 -288 16
WIRE -128 32 -128 16
WIRE -288 128 -288 96
WIRE -128 128 -128 96
WIRE -288 160 -320 160
WIRE -128 160 -288 160
WIRE -128 176 -128 160
WIRE -288 192 -288 160
WIRE -288 272 -288 256
WIRE -128 272 -128 240
FLAG -336 -160 V1
FLAG -320 16 V1
FLAG -320 160 V1
FLAG -288 -32 0
FLAG -144 -32 0
FLAG -288 128 0
FLAG -128 128 0
FLAG -288 272 0
FLAG -128 272 0
SYMBOL diode -304 -128 R0
WINDOW 0 38 19 Left 2
WINDOW 3 42 47 Left 2
SYMATTR InstName D_Silicon
SYMATTR Value 1N914
SYMBOL schottky -160 -128 R0
WINDOW 0 50 17 Left 2
WINDOW 3 47 46 Left 2
SYMATTR InstName D_Shottky
SYMATTR Value MBR0520L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL zener -304 32 R0
WINDOW 0 41 21 Left 2
WINDOW 3 38 52 Left 2
SYMATTR InstName D_Zener
SYMATTR Value BZX84C10L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL diode -144 32 R0
WINDOW 0 48 12 Left 2
WINDOW 3 46 46 Left 2
SYMATTR InstName D_SiC
SYMATTR Value UPSC600
SYMBOL varactor -304 192 R0
WINDOW 0 39 21 Left 2
WINDOW 3 44 57 Left 2
SYMATTR InstName D_varactor
SYMATTR Value MV2201
SYMATTR Type diode
SYMBOL LED -144 176 R0
WINDOW 0 83 8 Left 2
WINDOW 3 85 42 Left 2
SYMATTR InstName D_LED
SYMATTR Value NSCW100
SYMATTR Description Diode
SYMATTR Type diode
TEXT -112 0 Left 2 !.dc V1 -2 4 0.1
TEXT -96 136 Left 2 !V1 V1 0 DC 1

Dioden in LTSPICE

Netzliste (netlist)
* \Elek3_WS2011\LTSPICE\Dioden_arten_01.asc
D_Silicon N001 0 1N914
D_Shottky N001 0 MBR0520L
D_Zener N001 0 BZX84C10L
D_SiC N001 0 UPSC600
D_varactor N001 0 MV2201
D_LED N001 0 NSCW100
V1 N001 0 1
.model D D
.lib c:\lib\cmp\standard.dio
.dc V1 -2 4 0.1
.backanno
.end
Dioden fangen in der Netzliste mit dem Buchstaben D an.
Es gibt eine Bibliothek (library) standard.dio mit Bauteileigenschaften.

Quelle: Vollrath

Dioden Kennlinie logarithmisch in LTSPICE

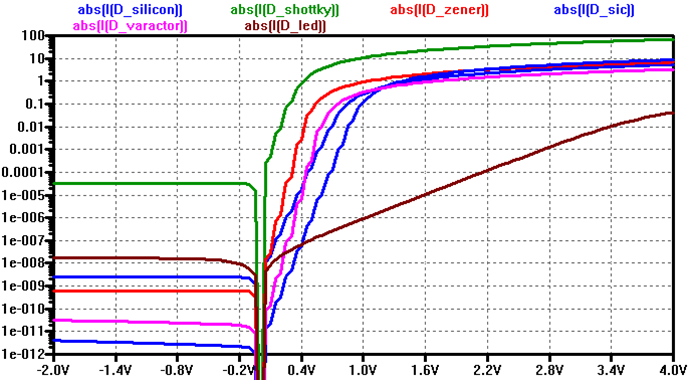
Quelle: Vollrath

	Silizium	Shottky	Zener	SiC	Varaktor	LED
I_s (A)	2.25n	31.7u	0.6n	2p	1.36p	16.9n
n	1.752	0.78	1	1.5	1	6.79

Dioden Kennlinie linear in LTSPICE

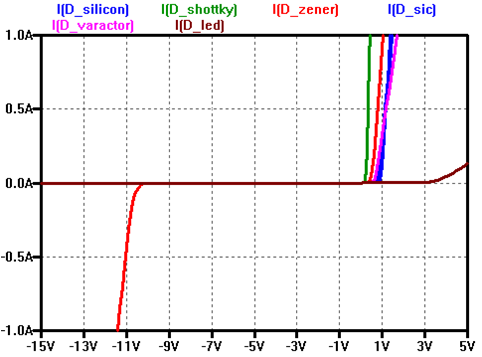
Quelle: Vollrath

Kapazitäten

Sperrschichtkapazität
(Junction Capacitance)

C_S, C_J

$C_{j0}$ : Diodenkapazität bei 0V

$C_S = C_J = \frac{C_{J0}}{\sqrt{1-\frac{U}{U_D}}}$

Es bildet sich eine Raumladungszone mit festen Ladungsträgern.
Durch die äußere Spannung wird die Größe der Raumladungszone und damit die Kapazität verändert.
Dies wirkt wie ein Plattenkondensator.

Diffusionskapazität
Bei einem Stromfluss befindet sich ein Überschuss an Ladungsträger in der Diode. Bei Änderung der angelegten Spannung verändert sich dieser Ladungsträgerüberschuss.

$C_D = \frac{d(Q)}{dU} = \tau_D \frac{I}{U_T}$

τ_D: Transitzeit
U_{T: Temperaturspannung}

Schaltverhalten: Einschalten und Ausschalten

DiodeSchalt.asc

Version 4
SHEET 1 1356 680
WIRE 48 64 32 64
WIRE 128 64 48 64
WIRE 240 64 208 64
WIRE 256 64 240 64
WIRE 32 96 32 64
WIRE 256 96 256 64
WIRE 32 192 32 176
WIRE 144 192 32 192
WIRE 256 192 256 160
WIRE 256 192 144 192
WIRE 144 208 144 192
FLAG 144 208 0
FLAG 48 64 U1
FLAG 240 64 UD
SYMBOL voltage 32 80 R0
WINDOW 3 -50 169 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value PULSE(-1.9 1.9 0.1u 1n 1n 0.05u 0.1u)
SYMATTR InstName V1
SYMBOL res 224 48 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL diode 240 96 R0
SYMATTR InstName D1
SYMATTR Value 1N4148X
TEXT -24 280 Left 2 !.tran 0 0.18u 80n 0.00001u
TEXT -32 312 Left 2 !.model 1N4148X D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=40n \n+ Iave=200m Vpk=75 mfg=Motorola type=silicon)
TEXT -32 368 Left 2 !;dc V1 -3 3 0.1

SPICE Simulation
t_d Aufladung der Diffusionskapazität
Stationärer Strom I₁

$\tau_S = \tau_D ln\left( 1- \frac{I_1}{I_2} \right)$
t_S Speicherzeit: Entladung der Diffusionskapazität
t_f Abfallzeit t_f ~ C_S(R_V+R_B)

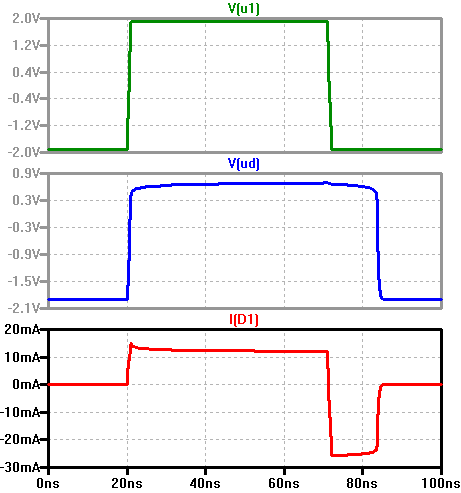td Stromspitze Einschalten, ts konstanter Gegenstrom, tf Abfall des Gegenstroms

Schaltverhalten: Messung

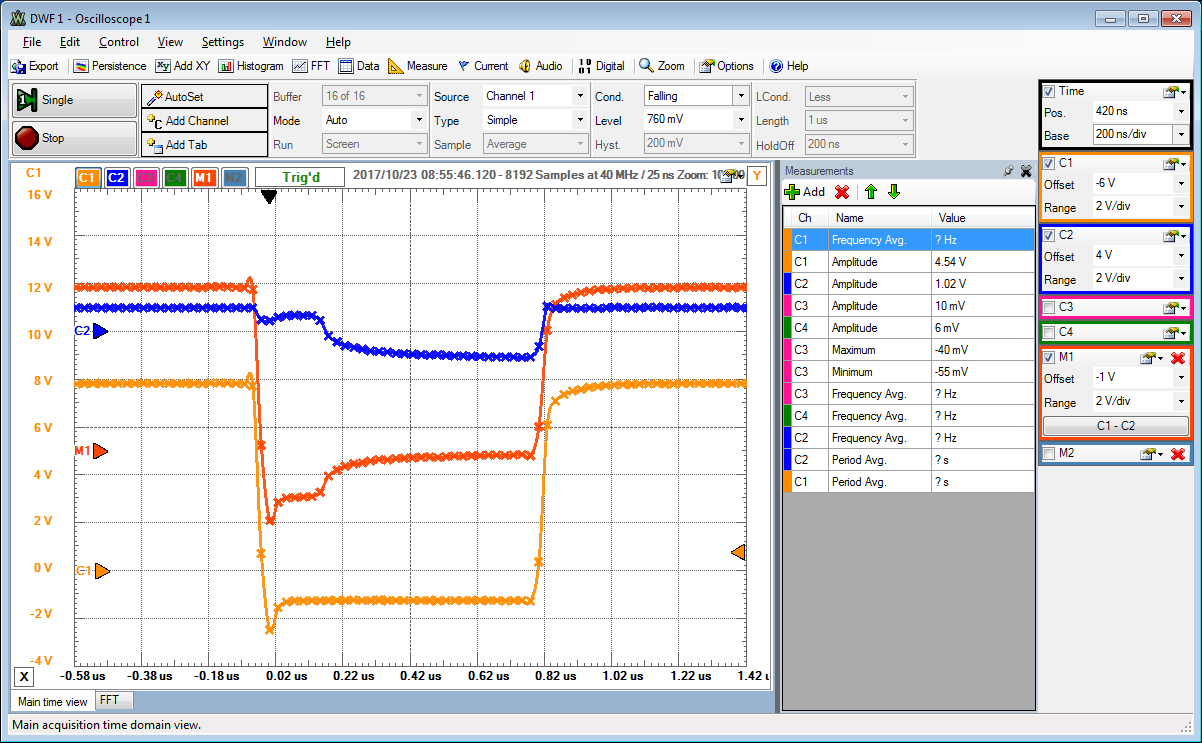
Mittlere Diode aus dem Diodenversuch.
Kleinster Widerstand 100 Ω am Ende des Sockels.
C1 zeigt das Rechteckeingansgsignal zwischen +8 V und -2 V mit einer Frequenz von 500kHz.
C2 zeigt die Diodenspannung.
Ohne eine Speicherladung im pn Übergang, sollte der Strom (M1) durch die Diode bei Sperrspannung sofort Null werden.
Da gespeicherte Ladung vorhanden ist, sieht man noch einen Stromfluss.
Dieses Verhalten entspricht einem Kapazitätsverhalten, man spricht von der Diffusionskapazität.

Ersatzschaltbilder

Warum benötigt man Ersatzschaltbilder?
Was sind Ersatzschaltbilder?
Wie kann man Ersatzschaltbilder klassifizieren?

Ein elektrisches Bauteil wird mit Hilfe von linearen Elementen: gesteuerten Quellen, Schaltern, Widerständen, Kapazitäten und Induktivitäten modelliert.
Schaltungen mit linearen Bauelementen kann man berechnen.

Kleinsignalersatzschaltbild

Was passiert bei kleinen Spannungs oder Stromänderungen um einen festen Arbeitspunkt?
Diodenspannung 1V
überlagertes Signal 10mV

Großsignalersatzschaltbild

Wie kann man die Diodengleichung durch ideale Bauteile annähern?

Ersatzschaltbild und Kleinsignalverhalten

Ein Widerstand R = 10

$\Omega$ und eine Diode sind in Reihe an einer Spannungsquelle V1 = 1 V angeschlossen.
Der Strom I soll berechnet werden?

$I = I_S\left( e^{\frac{q (V_1 - I * R )}{nkT}}-1\right)$
Dies ist eine nichtlineare Gleichung.
Die Lösung der Gleichung kann nur iterativ durch Ausprobieren erfolgen.

Näherungslösungen:

Grosssignalberechnung
Kleinsignalberechnung

Diode_Messaufbau.asc

Version 4
SHEET 1 880 680
WIRE 144 80 80 80
WIRE 288 80 224 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 SCOPE1DC
FLAG 80 80 SCOPE2DC
SYMBOL voltage 80 112 R0
SYMATTR InstName VAWG1
SYMATTR Value 1
SYMBOL res 240 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1
SYMATTR Value 1N914
TEXT 40 296 Left 2 !.dc VAWG1 0.2 1.0 0.05

Berechnung einer Diodenschaltung: Graphische Lösung

Graphische Lösung:

Was passiert wenn nur die Diode vorhanden wäre?
Wie groß ist der Strom durch den Widerstand bei verschiedenen Diodenspannungen?
Widerstandslastkennline
Wenn 0V an der Diode anliegt fliesst der maximale Strom

$I = \frac{1 V}{ 10 \Omega} = 100 mA$ .
Wenn 1V an der Diode anliegt fliesst kein Strom I = 0.
Zwischen diesen 2 Punkten ist die Kennlinie linear, da der Widerstand ein lineares Bauelement ist. Das Ohmsche Gesetz gilt.

Man kann nun den Arbeitspunkt der Schaltung aus dem Schnittpunkt der Kurven bestimmen.

$U_{Diode} = 0.75 V$ und

$I = 25 mA$

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Die Diodenkennlinie ist sehr steil.
Was passiert, wenn als Diodenspannung 0.7 V angenommen wird?
Dies entspricht einer Spannungsquelle von 0.7 V.

Diodenspannung	Strom
0.7 V	20 mA
0.75 V	25 mA
0.8 V	30 mA

Die Abweichungen zur graphischen Lösung sind gering.
Je größer die Spannung und der Widerstand sind, desto geringer ist die Abweichung.

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Was passiert mit dem Strom, wenn sich die Spannung V1 geringfügig ändert?

Man ersetzt die nichtlineare Diodenkennlinie durch eine Tangente im Arbeitspunkt.
Man ersetzt die Diode durch einen Widerstand.

$r_D = \frac{ \Delta U}{ \Delta I} = \frac{1}{\frac{\delta I}{ \delta U}} = \frac{1}{\frac{\delta I_S \left( e^{\frac{U}{n U_T}} -1 \right)}{ \delta U}}$

$r_D = \frac{1}{\frac{ I_S \left( e^{\frac{U}{n U_T}}\right)}{ n U_T}} = \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}}\right) }$

$r_D \approx \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}} - 1 \right) } = \frac{n U_T}{I_{Diode}} = 1 \Omega$

Man kann nun die Stromänderung der Schaltung im Arbeitspunkt mit der Spannungsteilerregel bestimmen.

$\Delta I = \Delta U \cdot \frac{ r_D}{ R + r_D}$

$\Delta I = 0.2 V \cdot \frac{ 1 \Omega }{ 10 \Omega + 1 \Omega} =0.018 mA$

Ersatzschaltbilder

Grosssignalersatzschaltbild:

Diode_GESB.asc

Version 4
SHEET 1 880 680
WIRE 48 144 0 144
WIRE 128 144 96 144
WIRE 224 144 208 144
SYMBOL voltage 112 144 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 -32 56 VBottom 2
SYMATTR InstName V1
SYMATTR Value 0.7 V
LINE Normal 96 144 48 112

Schalter mit Spannungsquelle (0.7 V)

Kleinsignalersatzschaltbild:

Diode_KESB.asc

Version 4
SHEET 1 880 680
WIRE 336 144 304 144
WIRE 448 144 416 144
SYMBOL res 432 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RD
SYMATTR Value ""

Widerstand

$r_D \approx \frac{n U_T}{I_{Diode}}$

Temperaturverhalten der Diode

Sperrstrom und Durchlassstrom steigen mit der Temperatur.

$I_D = I_S \left( e^{\frac{U}{nU_T}} -1 \right)$

$I_S \sim B·T^3·exp^{-\frac{W_g}{kT}}$

$U_T \sim T$
Die dargestellte Kennlinie hat für positive Werte eine andere y Achsenskala als für negative Werte.

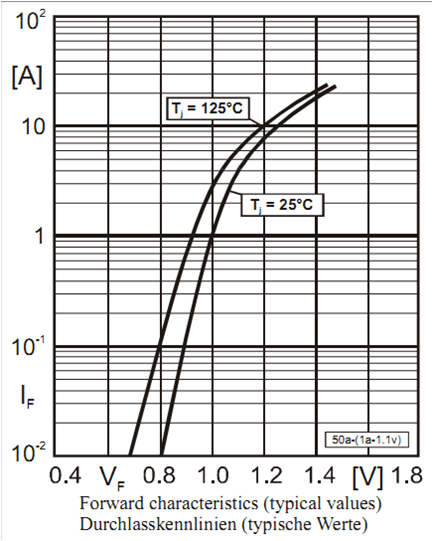Quelle: Datenblatt

Beim automatischen Testen von integrierten Schaltkreisen könen die Schutzdioden an den Pins zur Messung der Testtemperatur benutzt werden. Bei einem konstanten Strom wird die Spannung gemessen.
Dadurch wird sichergestellt, dass man wirklich die Solltemperatur für den Test erreicht hat.

Diodengleichungen

Symbol

Diode_Symbol.asc

Diodenstrom

$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

Temperaturspannung

$V_T = \frac{kT}{q}$

$( V_T(RT)= 25mV )$

Nächste Vorlesung:

Was ist ein MOSFET?
Bauteilparameter

23 MOSFET

Hochschule für angewandte Wissenschaften Kempten, Jörg Vollrath, Bahnhofstraße 61 · 87435 Kempten
Tel. 0831/25 23-0 · Fax 0831/25 23-104 · E-Mail: joerg.vollrath(a)hs-kempten.de

Impressum

2020 10 09 22 Diode Elektronik Prof. Dr. Joerg Vollrath

Elektronik

22 Diode

Prof. Dr. Jörg Vollrath

Video der 22. Vorlesung 22.12.2020

Heute

Praxisbeispiel: Dioden

Strom-Spannungskennlinie der Diode

SPICE Diodenmodell

Bestimmung der Parameter der Diodengleichung

Beispiel: Diodenmessung

Diodenkennlinie

Diodensymbole (LTSPICE) und Gleichung

Dioden in LTSPICE

Dioden Kennlinie logarithmisch in LTSPICE

Dioden Kennlinie linear in LTSPICE

Kapazitäten

Schaltverhalten: Einschalten und Ausschalten

Schaltverhalten: Messung

Ersatzschaltbilder

Ersatzschaltbild und Kleinsignalverhalten

Berechnung einer Diodenschaltung: Graphische Lösung

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Ersatzschaltbilder

Temperaturverhalten der Diode

Diodengleichungen

Nächste Vorlesung: