Elektronik

23 MOSFET

Prof. Dr. Jörg Vollrath

22 Diode

Video der 23. Vorlesung 11.1.2021

Länge: 00:00:00

0:0:0 Diode

0:5:0 Leuchtdioden, Gleichrichter,

0:6:15 MOSFET 4 Anschlüsse Gate, Drain, Source

0:7:40 Heute MOSFET

0:11:40 MOSFET Anschlüsse, NFET, PFET

0:15:45 CMOS Transistoren als Schalter

0:17:45 Gleichungen des NFET

0:22:45 Wichtige Kenngrößen

0:28:0 Kennlinien

0:33:21 Parameterextraktion MOSFET

0:36:12 Bestimmung der Transistorparameter

0:40:10 Wurzel IDS, Steigung Wurzel beta, Achsenabschnitt Uth

0:44:28 MOSFET Transistor als Diode

0:46:50 Beispiel NMOSFET Transistor

0:52:43 Kapazitäten elektronischer Bauelemente

0:55:9 LTSPICE MOSFET Modell

0:57:3 LTSPICE Modellkarte

0:58:30 Transistorentwicklung

1:3:10 MOSFET als Verstärker

1:11:8 Kleinere Änderungen, Linearisierung

1:12:12 Großsignalverhalten und Kleinsignalverhalten

1:16:45 Kleinsignalersatzschaltbild

1:19:50 Kleinsignalverhalten: Ausgangsleitwert

1:21:50 Warum habe ich einen Verstärker?

Heute

MOSFET Schaltsymbol Kennlinie MOSFET Parameter Bestimmung der MOSFET Parameter MOSFET als Schalter MOSFET als Verstärker LTSPICE Modell
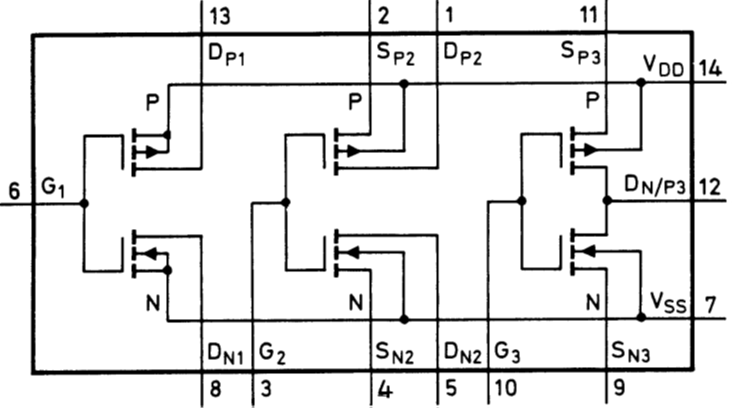	2N7000, FDG6320C, 3N1637	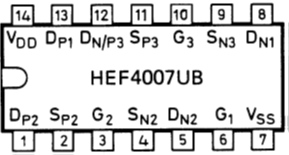CD4007, ALD110

MOSFET

MOSFET

Metall, Oxid, Semiconductor (Halbleiter) Feldeffekttransistor

Draufsicht

4 Anschlüsse
G: Gate, S. Source
D: Drain, B: Bulk (Substrat)

Funktionsweise NFET PFET

Das Gate ist isoliert und steuert den Stromfluss zwischen Drain und Source
Source und Bulk sind normalerweise verbunden

NPMOSFET.asc

Version 4
SHEET 1 880 680
SYMBOL nmos4 16 112 R0
WINDOW 0 65 15 Left 2
WINDOW 3 54 84 Left 2
SYMATTR InstName M1
SYMBOL pmos4 208 112 R0
WINDOW 0 66 21 Left 2
WINDOW 3 59 80 Left 2
SYMATTR InstName M2
TEXT -16 184 Left 2 ;G
TEXT 176 184 Left 2 ;G
TEXT 56 88 Left 2 ;D
TEXT 248 232 Left 2 ;D
TEXT 56 232 Left 2 ;S
TEXT 248 88 Left 2 ;S
TEXT 80 160 Left 2 ;B
TEXT 272 160 Left 2 ;B

CMOS Transistoren als Schalter

	Symbol	Eingang: Gate
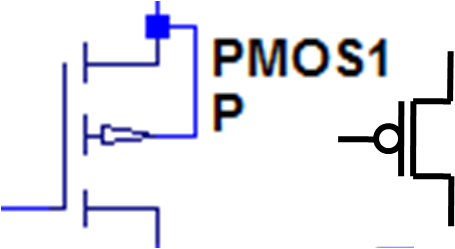
PFET Transistor: Eingang 1: Schalter offen Eingang 0: Schalter geschlossen Logikschaltung: PFETs im Schaltplan oben, verbunden mit VDD		0	1
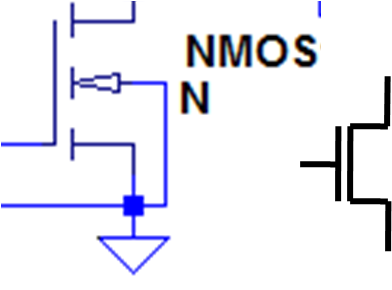
NFET Transistor: Eingang 1: Schalter geschlossen Eingang 0: Schalter offen Logikschaltung: NFETs im Schaltplan unten, verbunden mit GND, VSS, 0V.		0	1

Zur Realisierung von booleschen Funktionen werden MOSFET (metal oxide semiconductor field effect transistor) Transistoren eingesetzt.
Dabei werden Halbleiter (semiconductor, Silizium) verwendet, bei denen man durch Einbringen von Femdatomen (Dotierung) die Leitfähigkeit (Elektronen, Löcher) verändern kann.
Der MOS Transistor hat drei Anschlüsse Gate, Drain und Source.
Das Gate ist der Eingang. An der Drain ist der Ausgang und an der Source ist VDD (Betriebsspannnung, PFET) oder GND (0 V, NFET).
FET Feldeffekttransistor ist der Überbegriff für Halbleiterbaulemente, bei denen das elektrische Feld zwischen Gate und Kanal den Kanalwiderstand steuert bzw die Verbindung zwischen Drain und Source trennt oder schliesst.
Es gibt PFETs (PMOSFETs, Löcherleitung, positive Ladungsträger, Löcher) und NFETs (NMOSFETs, negative Ladungsträger, Elektronen) deren Verhalten komplementär sind (complementary metal oxide semiconductors, CMOS).
Ist die Gatesourcespannung beim NFET positiv, größer als eine Schwellspannung (threshold voltage), wird die Verbindung zwischen Drain und Source leitend (Ein Schalter wird geschlossen).
Ist die Gatesourcespannung beim PFET negativ, kleiner als eine Schwellspannung, wird die Verbindung zwischen Drain und Source leitend (Ein Schalter wird geschlossen).
Durch geschicktes Kombinieren der Transistoren können Logikfunktionen technisch realisiert werden.
Fast alle modernen Mikroprozessoren und digitalen Schaltungen werden mit CMOS Transistoren realisiert.

Typen des Feldeffekttransistors

Isolation

Dielektrisch: MOSFET, MISFET, IGFET
Gesperrter pn-Übergang: Sperrschicht-FET, JFET, MESFET

Die Schwellspannung des Gate

Selbstleitender FET: Depletion FET

Bei der Gatespannung U_GS=0V ist ein leitender Kanal vorhanden

Selbstsperrender FET: Enhancement FET

Bei der Gatespannung U_GS=0V ist kein leitender Kanal vorhanden

Kanalart

p-leitender Kanal PFET
n-leitender Kanal: NFET

Die Gleichung des n-Kanal MOSFETs

$I_{DS} = \cases{ 0 & \text{ Sperrbereich } \cr \text{ für } U_{GS} \leq U_{th} \cr \cr \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) & \text{ Sättigung} \cr \text{ für } 0 \leq U_{GS} - U_{th} \lt U_{DS} \cr \cr \beta \left( 2 \left( U_{GS}-U_{th} \right) U_{DS} - U_{DS}^2 \right) & \text{ Triodenbereich} \cr \text{ für } 0\leq U_{GS} - U_{th} \geq U_{DS} }$

$\beta = \frac{\mu_n \epsilon_{ox}}{2d_{ox}} \frac{W}{L} = \frac{1}{2} \mu_n C_{ox}^{'} \frac{W}{L} = \frac{1}{2} K_{n}^{'} \frac{W}{L} = \frac{1}{2} K_{n} = \frac{1}{2} KP$

Übertragungs-
kennlinie

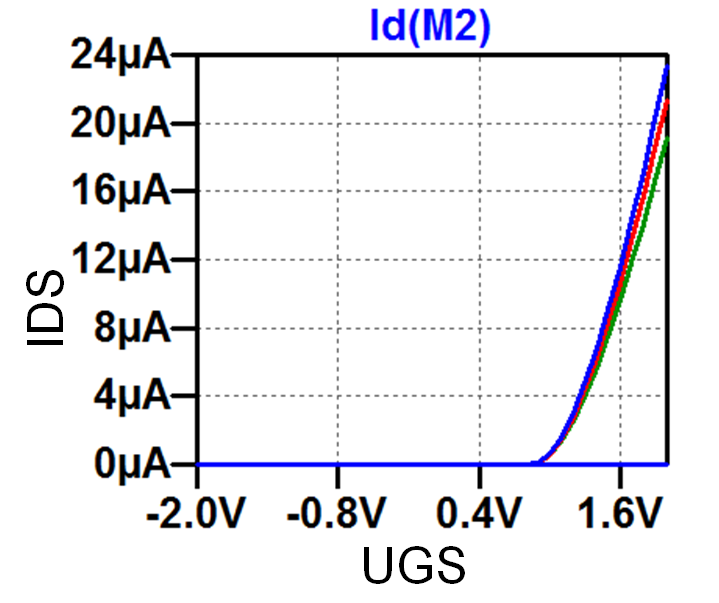Quelle Vollrath

Ausgangs-
kennlinie

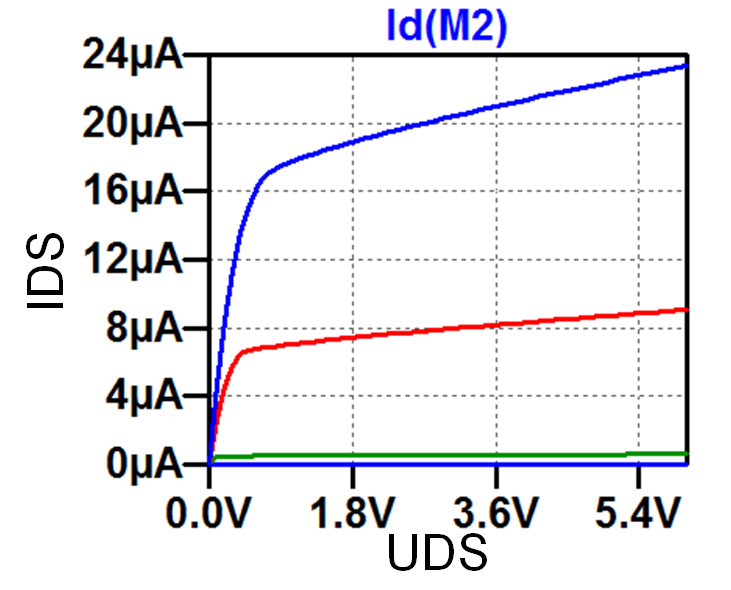Quelle Vollrath

Wichtige Kenngrößen

U_th : Schwellspannung [V]
β : Steilheitsparameter [A V^-2]

$\mu_n$ : Beweglichkeit (NFET)
Oxidkapazität pro Fläche $C_{ox}^{'}=\frac{\epsilon_{ox}}{2d_{ox}}$
W: Transistorweite
L: Transistorlänge

λ : Kanallängenmodulation [V^-1]
Integrierte Schaltungen

W und L werden vom Schaltungsentwickler bestimmt (gezeichnet)
C_ox: wird durch die Technologie bestimmt

SPICE:
M2 0 N001 N002 0 P_1u l=1u w=1u

SPICE:
Mxxx Nd Ng Ns Nb <model> [m=<value>] [L=<len>] [W=<width>]
Anschlüsse, Knoten, Geometrie
m: Anzahl Transistoren in Parallelschaltung

Kennlinien:

Übertragungskennlinie

Quelle Vollrath

Ausgangskennlinie

Quelle Vollrath

Beispiel: NMOSFET-Transistor

Berechnen Sie den Drain Source Strom für einen NMOS Transistor mit U_GS=5V, U_DS=10V, U_th=1V, K_n=1mA/V² und

$\lambda =0.02V^{-1}$ .
In welchem Arbeitsbereich befindet sich der Transistor?

$U_{DS} > U_{GS} - U_{th} Sättigung$

$I_{DS}= \beta \left(U_{GS} - U_{th}\right)^2 \left( 1+ \lambda U_{DS} \right)$

$I_{DS}= \frac{1}{2} K_n\left(U_{GS} - U_{th}\right)^2 \left( 1+ \lambda U_{DS} \right)$

$I_{DS} = \frac{1mA}{2V^2} \left(5V - 1V\right)^2 \left( 1+ 0.02 V^{-1} 10V \right)$

$I_{DS}= \frac{1}{2} 16 \cdot 1.2mA=9.6mA$

Beispiel: MOSFET Bauteil und Kennlinie

An einem MOSFET messen Sie bei einer Gate-Sourcespannung von 2V bei U_DS=3V I_DS=4mA und bei U_DS=5V I_DS=4.4mA. Bei U_GS=1.5V und U_DS=3V messen Sie I_DS=1mA.
Berechnen Sie

$\lambda$ , V_th und K_N.

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\frac{I_{DS1}}{I_{DS2}}= \frac{ \left( 1+\lambda U_{DS1} \right)}{\left( 1+\lambda U_{DS2} \right)}$

$\left( 1+\lambda U_{DS2} \right) \frac{I_{DS1}}{I_{DS2}}= 1+\lambda U_{DS1}$

$\lambda \left( U_{DS2} \frac{I_{DS1}}{I_{DS2}} - U_{DS1} \right) = 1- \frac{I_{DS1}}{I_{DS2}}$

$\lambda =\frac{ 1- \frac{I_{DS1}}{I_{DS2}} }{U_{DS2} \frac{I_{DS1}}{I_{DS2}} - U_{DS1}} = \frac{ 1- \frac{4}{4.4} }{5 \frac{4}{4.4} - 3} V^{-1} =\frac{1}{11} \frac{11}{17} V^{-1}$

$=\frac{1}{17}=0.06 V^{-1}$

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\lambda =0.06 V^{-1}$

$\frac{I_{DS1}}{I_{DS3}}= \frac{ \left( U_{GS1}-U_{th} \right)^2}{\left( U_{GS3}-U_{th} \right)^2}$

$\sqrt{\frac{I_{DS1}}{I_{DS3}}}= \frac{ U_{GS1}-U_{th} }{U_{GS3}-U_{th}}$

$\left( U_{GS3}-U_{th} \right) \sqrt{\frac{I_{DS1}}{I_{DS3}}}= U_{GS1}-U_{th}$

$U_{th} \left( 1-\sqrt{\frac{I_{DS1}}{I_{DS3}}} \right) = U_{GS1}- U_{GS3} \sqrt{\frac{I_{DS1}}{I_{DS3}}}$

$U_{th} = \frac {U_{GS1}- U_{GS3} \sqrt{\frac{I_{DS1}}{I_{DS3}}}}{1-\sqrt{\frac{I_{DS1}}{I_{DS3}}}} = \frac{ 2V -1.5V \cdot 2}{1-2}=1V$

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\lambda =0.06 V^{-1}$

$U_{th} = 1 V$

$\beta = \frac{\left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)}{I_{DS}}$

$\beta = \frac{4mA}{\left( 2V-1V \right)^2 \left( 1+0.06 \cdot 3V \right)} = \frac{4}{1.18} \frac{mA}{V^2} = 3.39 \frac{mA}{V^2}$

MOSFET Parameterextraktion

Extraktion aus Messpunkten im Sättigungsbereich:

$U_{GS} = const$ ;

$U_{DS1}, U_{DS2} \rightarrow \frac{I_{DS1}}{I_{DS2}} \rightarrow \lambda$

$U_{DS} = const$ ;

$U_{GS1}, U_{GS2} \rightarrow \frac{I_{DS1}}{I_{DS2}} \rightarrow U_{th}$

$\beta$

Auftragung der Messwerte als lineare Funktion:

$y = \sqrt{I_{DS}} = \sqrt{\beta} \left( U_{GS} - U_{th} \right) \sqrt{\left( 1 + \lambda U_{DS} \right)}$

$y = \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{GS} - \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{th}$

$x = U_{GS}$ ,

$a = \sqrt{\beta \left( 1 + \lambda U_{DS} \right) }$ ,

$b = - \sqrt{\beta \left( 1 + \lambda U_{DS} \right)} U_{th} = - a \cdot U_{th}$

$y = ax + b$

1. Mathematische Methode:
Bei 2 Messungen bei gleicher Spannung U_GS und unterschiedlicher Spannnung U_DS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme λ.
Bei 2 Messungen bei gleicher Spannung U_DS und unterschiedlicher Spannnung U_GS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme U_th.
β kann man dann aus einer Messung durch einsetzen von I_DS, U_th, λ und U_GS berechnen.
2. Methode durch grafische Interpretation

Bei 2 Messungen bei gleicher Spannung U_GS im Sättigungsbereich erhält man aus dem Verhältnis der Ströme λ. Trägt man die Wurzel des Stromes I_DS über der Gate-Source-Spannung auf ergibt sich eine Geradengleichung.
Aus der Steigung dieser Geraden und dem y-Achsenabschnitt bei x = U_GS0 ergeben sich U_th und bei kleinem λ und Vernachlässigung von λ U_DS gegenüber 1 dann β.

NMOSFET SPICE Modell

Typische Werte

$KP = 20..50 \mu A /V^2$
KP = K_N = 2 · β
λ = 0

$V_{th} = 1V$

$C_{GD0} = C_{GS0} = 0 F$

$C_{GB0} =C_{JSW} = 0 F$

LEVEL = 1 einfache Gleichungen
.model Ntyp NMOS(LEVEL=1 KP=50u VT0=1 LAMBDA=0.002
+ CGSO=45n CGBO=2n CGDO=45n)

CD4007

.model CD4007N NMOS(LEVEL=1 KP=500u VT0=1 LAMBDA=0.002
+ CGSO=45n CGBO=2n CGDO=45n)

NMOSmodel01.asc

Version 4
SHEET 1 880 680
WIRE 400 -96 400 -112
WIRE 448 -16 400 -16
WIRE 528 -16 512 -16
WIRE 288 80 272 80
WIRE 400 80 400 -16
WIRE 400 80 352 80
WIRE 448 80 400 80
WIRE 528 80 528 -16
WIRE 528 80 512 80
WIRE 400 112 400 80
WIRE 80 128 80 112
WIRE 272 160 272 80
WIRE 272 160 240 160
WIRE 528 160 528 80
WIRE 576 160 528 160
WIRE 160 176 80 176
WIRE 32 208 16 208
WIRE 272 224 272 160
WIRE 288 224 272 224
WIRE 400 224 400 192
WIRE 400 224 352 224
WIRE 448 224 400 224
WIRE 528 224 528 160
WIRE 528 224 512 224
WIRE 80 256 80 224
WIRE 400 304 400 224
WIRE 448 304 400 304
WIRE 528 304 528 224
WIRE 528 304 512 304
WIRE 400 384 368 384
WIRE 272 416 272 224
WIRE 288 416 272 416
WIRE 528 416 528 304
WIRE 528 416 352 416
FLAG 240 160 G
FLAG 576 160 B
FLAG 368 384 S
FLAG 400 -112 D
FLAG 80 112 D
FLAG 160 176 B
FLAG 80 256 S
FLAG 16 208 G
SYMBOL nmos4 32 128 R0
SYMATTR InstName M1
SYMBOL cap 352 64 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName CGD
SYMATTR Value ""
SYMBOL cap 352 208 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName CGS
SYMATTR Value ""
SYMBOL cap 352 400 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName CGB
SYMATTR Value ""
SYMBOL current 400 112 R0
SYMATTR InstName I1
SYMATTR Value ID
SYMBOL diode 512 64 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 Invisible 2
SYMATTR InstName DDB
SYMBOL diode 512 208 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName SB
SYMATTR Value ""
SYMBOL cap 512 -32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 Invisible 2
SYMATTR InstName CGD
SYMATTR Value ""
SYMBOL cap 512 288 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName CSB
SYMATTR Value ""
SYMBOL res 384 -112 R0
WINDOW 3 36 76 Invisible 2
SYMATTR InstName RD
SYMATTR Value ""
SYMBOL res 384 288 R0
SYMATTR InstName R2
SYMATTR Value ""

SPICE MOS Modell

.model AO6407 VDMOS(pchan Rg=3 Rd=14m Rs=10m 
+ Vto=-.8 Kp=32 Cgdmax=.5n Cgdmin=.07n Cgs=.9n 
+ Cjo=.26n Is=26p Rb=17m mfg=Alpha_&_Omega 
+ Vds=-20 Ron=34m Qg=13n)

.MODEL N_1u NMOS LEVEL  = 3                  
+ TOX  = 200E-10 NSUB = 1E17    GAMMA = 0.5          
+ PHI  = 0.7     VTO  = 0.8     DELTA = 3.0         
+ UO   = 650     ETA  = 3.0E-6  THETA = 0.1          
+ KP   = 120E-6  VMAX = 1E5     KAPPA = 0.3                
+ RSH  = 0       NFS  = 1E12    TPG   = 1                  
+ XJ   = 500E-9  LD   = 100E-9                 
+ CGDO = 200E-12 CGSO = 200E-12 CGBO  = 1E-10              
+ CJ   = 400E-6  PB   = 1       MJ    = 0.5           
+ CJSW = 300E-12 MJSW = 0.5                                  
*

Weitere Modelle finden sich im Internet:

Baker: 1 µm MOSFET model, 50 nm MOSFET model, cmosedu_models.txt
Sedra Smith Level=1 5 µm, 0.5 µm: sedra_lib.lib
Allen, Holberg Level=3 0.8 µm: Holberg.txt
TSMC 0.25um CMOS MOSFETs (level 3) t14y_tsmc_025_level3.lib from MOSIS .
ALD1101, ALD1102, David A. Johns University of Toronto

CD4007

.model CD4007N NMOS(LEVEL=1 KP=500u VT0=1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)
.model CD4007P PMOS(LEVEL=1 KP=500u VT0=-1 LAMBDA=0.002 CGSO=45n CGBO=2n CGDO=45n)

ALD1106, ALD1107

.model ALD1106N NMOS(LEVEL=1 KP=0.48m VT0=0.7 LAMBDA=0.018 CGDO=100n CGSO=100n)
.model ALD1107P PMOS(LEVEL=1 KP=0.2m VT0=-0.7 LAMBDA=0.018 CGDO=100n CGSO=100n)

ALD1101, ALD1102

* ALD ALD1101 (NMOS) and ALD 1102 (NMOS) model
* This model was extracted from measurements.
* The model is correct only for W = 1738 um and L = 1 um.
* The device size above doesn't represent the actual device size.

* NMOS hand analysis values: Vtn = 0.71 V; UnCox(W/L) = 4.5 mA/V^2 ; VA = 80 V;
.MODEL ALD1101 NMOS LEVEL = 2 UO = 12.72 VTO = 0.6766 NFS = 1.154E12 TOX = 1E-08 NSUB = 3.892E17 UCRIT = 4.582E05 UEXP = 0.07025 VMAX = 6363 RS = 9.491 RD = 5.659 XJ = 4.787E-09 LD = 0 DELTA = 1E-12 NEFF = 0.8345 NSS = -3.801 CGSO = 1.15E-9 CGDO = 1.15E-9 CGBO = 0 CBD = 0 CBS = 0 CJ = 0 MJ = 0.5 CJSW = 0 MJSW = 0.6057 IS = 1.0E-14 PB = 0.8 FC = 0.5 NEFF=5

* PMOS hand analysis values: Vtn = -0.65 V; UpCox(W/L) = 2.10 mA/V^2 ; VA = -19 V;
.MODEL ALD1102 PMOS LEVEL = 2 UO = 5.536 VTO = -0.6093 NFS = 3.602E12 TOX = 1E-08 NSUB = 4.046E16 UCRIT = 8.118E04 UEXP = 0.1647 VMAX = 1399 RS = 9.249 RD = 38.77 XJ = 4.443E-09 LD = 0 DELTA = 8828 NEFF = 2.145 NSS = -8.793 CGSO = 1.15E-9 CGDO = 1.15E-9 CGBO = 0 CBD = 0 CBS = 0 CJ = 0 MJ = 0.5 CJSW = 0 MJSW = 0.33 IS = 1E-14 PB = 0.8 FC = 0.5

CMOS 1µm models (Holberg)

** Holberg, p 337 Table6.6-1
.model NMOS1 NMOS(LEVEL=1 VT0=0.70 KP = 110U GAMMA = 0.4 LAMBDA = 0.04 PHI = 0.7 MJ = 0.5
+ MJSW = 0.38 CGBO =700P CGSO=220P CGDO = 220P CJ = 770U CJSW = 380P LD = 0.016U TOX= 14N) 
.model PMOS1 PMOS (LEVEL=1 VT0 = -0.70 KP = 50U GAMMA = 0.57 LAMBDA = 0.05 PHI = 0.8 MJ = 0.5
+ MJSW = 0.35 CGBO =700P CGSO=220P CGDO = 220P CJ = 560U CJSW = 350P LD = 0.014U TOX= 14N)

Transistorentwicklung

Transistoren werden immer kleiner
Was bedeutet das für die elektrischen Eigenschaften.

Modelle werden komplizierter
Spannungen werden kleiner
Eingangskapazitäten werden kleiner
Leistungsverbrauch nimmt ab.
Höhere Frequenzen möglich

MOSFETs finden immer mehr Anwendungen

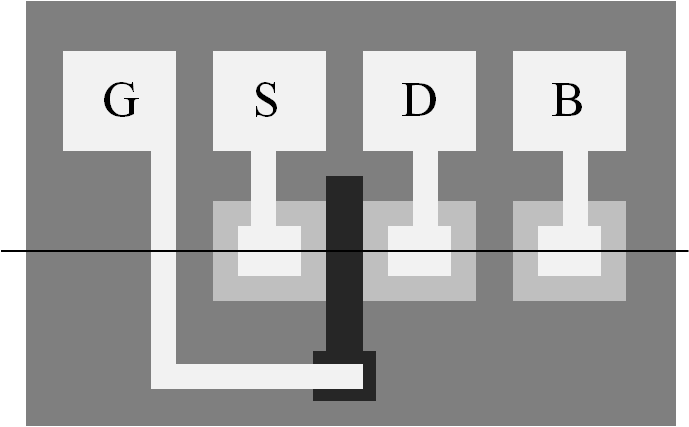1970 8 µm
1980 2

$\mu m$
1990 0.5

$\mu m$
2000 130

$nm$
2010 40

$nm$
2013 22

$nm$
2015 14

$nm$
2020 5

$nm$

Jahr und Strukturgröße

Wikipedia: 5 nm Process

MOSFET als Verstärker: Das Prinzip

R_D: Bestimmt die Ausgangsspannung Ua
U_a(t)= U_DD-I_DS(t)·R_D
$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$
Die Eingangsspannung erzeugt eine Stromänderung,
die mit R_D in eine Ausgangsspannung umgesetzt wird.

Verstaerker03.asc

Version 4
SHEET 1 888 680
WIRE 256 80 256 64
WIRE 256 176 256 160
WIRE 304 176 256 176
WIRE 256 192 256 176
WIRE 352 240 256 240
WIRE 208 272 176 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 256 304 256 288
FLAG 256 304 0
FLAG 176 272 UGS
FLAG 304 176 UA
FLAG 256 64 VDD
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMATTR Value CD4007N
SYMBOL res 240 64 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 20k
SYMATTR InstName RD
TEXT 120 432 Left 2 !VDD VDD 0 DC 5\nVGS UGS 0 SINE(1.6 0.1 1k)
TEXT 112 496 Left 2 !.dc VGS 0 5 0.1
TEXT 120 344 Left 2 !.model CD4007N NMOS(LEVEL=1 \n+ KP=500u VT0=1 LAMBDA=0.002\n+ CGSO=45n CGBO=2n CGDO=45n)
TEXT 144 160 Left 2 !;tran 5m

MOSFET als Verstärker: Die Kennlinie

$U_{a}= U_{DD} - \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) \cdot R_{D}$

R_D: Bestimmt die Ausgangsspannung Ua

Die Ausgangsspannung U_a hängt nicht linear mit der Eingangsspannung U_GS zusammen.

Die Eingangsspannung erzeugt eine Stromänderung,
die mit R_D in eine Ausgangsspannung umgesetzt wird.

$U_{th} = 1 V$ ,

$V_{DD} = 9 V$ ,

$\beta = 0.12 mAV^{-2}$ ,

$\lambda = 0.01 V^{-1}$ ,

$R_{Load} = 10 k\Omega$
Arbeitspunkt: U_GS=2.5V

$\Delta U_{GS} = 1V (+-0.5V)$

$\Delta I_{DS} = 0.5 mA - 0.1 mA = - 0.4 mA$

$\Delta U_{DS} = 4 V - 8 V = -4 V$
Spannngsverstärkung: VU = -4V/1V = -4

Großsignalverhalten und Kleinsignalverhalten

Großsignalverhalten

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\text{für} 0 \leq U_{GS} - U_{th} \lt U_{DS} \text{Sättigung}$

Kleinsignalverhalten

Kleine Signale
Näherung durch Tangente (Ableitung)

$\Delta I_{DS}= \frac{dI_{DS}}{dU_{GS}}|_{U_{GS}} \cdot \Delta U_{GS}$

$\frac{dI_{DS}}{dU_{GS}}= \frac{ d \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)} { dU_{GS}}$

$\frac{dI_{DS}}{dU_{GS}} = 2 \beta \left( U_{GS}-U_{th} \right) \left( 1+\lambda U_{DS} \right)$

$\frac{dI_{DS}}{dU_{GS}} = 2 \frac{I_{DS}}{U_{GS}-U_{th}}$

Kleinsignalersatzschaltbild
AC Analysis

Kleinsignalverhalten

Steilheit: g_m

Sättigung

$g_m = \frac{dI_{DS}}{dU_{GS}}= \frac{ \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)} {dU_{GS}}$

$g_m = 2 \beta \left( U_{GS}-U_{th} \right) \left( 1+\lambda U_{DS} \right)$

$g_m = \frac{2 I_{DS}}{U_{GS}-U_{th}} \simeq 2 \sqrt{\beta \cdot IDS}$

Große Steilheit für großen Strom

Ausgangsleitwert: g_d

$g_d = \frac{dI_{DS}}{dU_{DS}}= \frac{ \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)} {dU_{DS}}$

$g_d = \beta \left( U_{GS}-U_{th} \right)^2 \lambda = \frac{I_{DS}\lambda}{1+\lambda U_{DS}}$

$g_d \simeq I_{DS} \lambda$

MOSKlein.asc

Version 4
SHEET 1 880 680
WIRE 16 64 0 64
WIRE 48 64 16 64
WIRE 304 64 112 64
WIRE 384 64 304 64
WIRE 400 64 384 64
WIRE 112 80 112 64
WIRE 304 96 304 64
WIRE 112 192 112 160
WIRE 112 192 0 192
WIRE 304 192 304 176
WIRE 304 192 112 192
WIRE 400 192 304 192
FLAG 16 64 ugs
FLAG 384 64 uds
SYMBOL bi 112 80 R0
SYMATTR InstName B1
SYMATTR Value {gm}*V{ugs}
SYMBOL res 288 80 R0
SYMATTR InstName R1
SYMATTR Value {gd}
TEXT 56 48 Left 2 ;G
TEXT 192 48 Left 2 ;D
TEXT 136 216 Left 2 ;S
TEXT 176 216 Left 2 !PARAM gm=1m gd=1/1u
LINE Normal 0 176 0 80
LINE Normal -16 160 0 176
LINE Normal 16 160 0 176
LINE Normal 400 176 400 80
LINE Normal 384 160 400 176
LINE Normal 416 160 400 176

Spannungsverstärkung: V_u

$v_u = \frac{u_{DS}}{u_{GS}} = \frac{- g_m \cdot u_{GS}}{g_d \cdot u_{GS}} = - \frac{g_m}{g_d}$

$v_u = - \frac{2 I_{DS}}{(U_{GS}-U_{th}) I_{DS} \lambda}$

$v_u = - \frac{2}{(U_{GS}-U_{th}) \lambda}$

Nächste Vorlesung:

MOSFET Grundschaltungen

24 MOSFET

Kapazitäten elektronischer Bauelemente

Limit high-frequency performance of the electronic device they are associated with.
Limit switching speed of circuits in logic applications
Limit frequency at which useful amplification can be obtained in amplifiers.
MOSFET capacitances depend on region of operation and are non-linear functions of voltages at device terminals.

$C_{GS}= C_{GD} = 0.5 \cdot C_{ox}$

$C_{ox}= \epsilon_{ox} \frac{WL}{d_{ox}}$

W: Kanalweite, L: Kanallänge, d_ox = t_ox: Oxiddicke

MOSFET Frequenzverhalten

Grundlage ist die einfache Verstärkerschaltung mit den Transistorkapazitäten ohne Lastkapazität.
C_GD = C_GS = C_ox/2
Bei einer idealen Spannungsquelle am Eingang spielt C_GS keine Rolle.
Durch die Kapazitäten wird ein Tiefpass realisiert.

Es kann das Kleinsignalersatzschaltbild aufgestellt werden und die komplexe Kleinsignalübertragungsfunktion erstellt werden.
Durch die Kopplung von Eingang und Ausgang durch C_GD wird die Rechnung etwas komplizierter.

Ohne Kapazität ergebe sich eine Spannungsverstärkung:

$v_u = - g_m \cdot (R_L || r_d)$

$r_D = \frac{1}{g_D}$ ist der Kleinsignalausgangswiderstand
g_m ist der Übertragungsleitwert
R_L der Lastwiderstand

Ist die Eingangsspannungsänderung u_GS sehr klein, so wirkt die gesamte Kapazität C_GD, wie eine Last parallel zu R_L und g_D.

$v_u \approx - g_m \cdot (R_L || r_d || C_{GD} )$

$v_u \approx - \frac{g_m}{ \frac{1}{R_L} + g_d + j \omega C_{GD}}$
Dies ist eine Übertragungsfunktion mit einer Polstelle: eine Tiefpassfunktion.

Verstaerker03b.asc

Version 4
SHEET 1 880 680
WIRE 256 80 256 64
WIRE 256 176 256 160
WIRE 256 176 144 176
WIRE 352 176 256 176
WIRE 144 192 144 176
WIRE 256 192 256 176
WIRE 352 240 256 240
WIRE 144 272 144 256
WIRE 144 272 96 272
WIRE 208 272 144 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 144 304 144 272
WIRE 144 384 144 368
WIRE 256 384 256 288
WIRE 256 384 144 384
WIRE 256 400 256 384
FLAG 256 400 0
FLAG 96 272 UGS
FLAG 256 64 VDD
FLAG 352 176 UA
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMBOL res 240 64 R0
SYMATTR InstName RL
SYMATTR Value ""
SYMBOL cap 128 304 R0
WINDOW 0 23 8 Left 2
SYMATTR InstName CGS
SYMATTR Value 10p
SYMBOL cap 128 192 R0
SYMATTR InstName CGD
SYMATTR Value 10p

MOSFET Frequenzverhalten

Genauere Rechnung:

Spannungsverstärkung

$\underline{V}_u = \frac{\underline{U}_a}{\underline{U}_e} = \frac{\underline{U}_{DS}}{\underline{U}_{GS}} =$

Spannungsquelle U_GS

C_GS fällt weg
Umwandeln in eine Stromquelle:
$\underline{I}_e =\underline{U}_{GS} \cdot j \omega C_{GD}$

$\underline{U}_a = \underline{I} (R \parallel C) = (\underline{I}_e - g_m \underline{U}_{GS}) (R_{L} \parallel r_{d} \parallel C_{GD})$

$\underline{V}_u = \frac{\underline{U}_a}{\underline{U}_e} = \frac{(\underline{U}_{GS} j\omega C_{GD}-g_m\underline{U}_{GS})}{\underline{U}_{GS}} \frac{1}{\frac{1}{R_L} + g_d+ j\omega C_{GD}}$

$\underline{V}_u = \frac{ j\omega C_{GD} - g_m }{\frac{1}{R} + j\omega C_{GD}} = \frac{R \left( j\omega C_{GD} - g_m \right)}{1+R j \omega C_{GD}}$

mit

$R = \frac{1}{g_d+\frac{1}{R_L}}$

MOSFrequenz01a.asc

Version 4
SHEET 1 880 680
WIRE 96 48 32 48
WIRE 128 48 96 48
WIRE 432 48 192 48
WIRE 528 48 432 48
WIRE 608 48 528 48
WIRE 96 64 96 48
WIRE 432 64 432 48
WIRE 528 64 528 48
WIRE 192 80 192 48
WIRE 96 176 96 128
WIRE 192 176 192 160
WIRE 192 176 96 176
WIRE 432 176 432 144
WIRE 432 176 192 176
WIRE 528 176 528 144
WIRE 528 176 432 176
WIRE 192 192 192 176
FLAG 192 192 0
FLAG 32 48 UGS
FLAG 608 48 UDS
SYMBOL cap 192 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 Invisible 2
SYMATTR InstName CGD
SYMATTR Value 1000p
SYMBOL cap 112 128 R180
WINDOW 0 24 56 Left 2
WINDOW 3 24 8 Invisible 2
SYMATTR InstName CGS
SYMATTR Value 1p
SYMBOL bi 192 80 R0
WINDOW 3 24 78 Left 2
SYMATTR Value I= - {gm} * V(UGS)
SYMATTR InstName B1
SYMBOL res 416 48 R0
WINDOW 3 36 76 Invisible 2
SYMATTR Value 10k
SYMATTR InstName RD
SYMBOL res 512 48 R0
WINDOW 3 36 76 Invisible 2
SYMATTR Value 10k
SYMATTR InstName RL
TEXT 224 208 Left 2 ;S
TEXT 16 224 Left 2 !.param gm=0.1
TEXT 440 224 Left 2 !V1 UGS 0 AC 1
TEXT 248 224 Left 2 !.ac dec 10 1k 1G
TEXT 280 16 Left 2 ;I
LINE Normal 288 48 272 32
LINE Normal 272 64 288 48

MOSFrequenz02a.asc

Version 4
SHEET 1 880 680
WIRE 80 48 0 48
WIRE 192 48 80 48
WIRE 448 48 192 48
WIRE 544 48 448 48
WIRE 608 48 544 48
WIRE 448 64 448 48
WIRE 544 64 544 48
WIRE 0 80 0 48
WIRE 80 80 80 48
WIRE 192 80 192 48
WIRE 0 176 0 160
WIRE 80 176 80 144
WIRE 80 176 0 176
WIRE 192 176 192 160
WIRE 192 176 80 176
WIRE 448 176 448 144
WIRE 448 176 192 176
WIRE 544 176 544 144
WIRE 544 176 448 176
WIRE 192 192 192 176
FLAG 192 192 0
FLAG 608 48 UDS
SYMBOL cap 64 80 R0
SYMATTR InstName CGD
SYMATTR Value 1000p
SYMBOL bi 192 80 R0
WINDOW 3 24 78 Left 2
SYMATTR Value I= - {gm} * V(UGS)
SYMATTR InstName B1
SYMBOL res 432 48 R0
WINDOW 3 36 76 Invisible 2
SYMATTR Value 10k
SYMATTR InstName RD
SYMBOL res 528 48 R0
WINDOW 3 36 76 Invisible 2
SYMATTR Value 10k
SYMATTR InstName RL
SYMBOL current 0 80 R0
WINDOW 123 24 108 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName Ie
SYMATTR Value 1
TEXT 224 208 Left 2 ;S
TEXT 16 224 Left 2 !.param gm=0.1
TEXT 248 224 Left 2 !.ac dec 10 1k 1G
TEXT 280 16 Left 2 ;I
LINE Normal 288 48 272 32
LINE Normal 272 64 288 48

MOSFET Frequenzverhalten

$\underline{V}_u = \frac{Rj\omega C_{GD}-Rg_m}{1+Rj\omega C_{GD}} = \frac{j\omega - \frac{g_m}{C_{GD}}}{j\omega + \frac{1}{RC_{GD}}}$
Grenzfrequenz für g_m >> C_GD

$\omega_g = \frac{1}{R C_{GD}}$

Je kleiner der Transistor, desto kleiner C_GD

Spannungsverstärkung:

$v_u(0) = -R \cdot g_m = - \frac{g_m}{g_D}$

Verstärkungsbandbreiteprodukt ( gain band width GBW)
Transitfrequenz: v_u=1

$\omega_T = \omega_g \cdot v_u(0) = \frac{g_m}{C_{GD}} \sim \frac{V_{GS}-V_{th}}{L^2}$

Eine Last C_L am Ausgang würde parallel zu C_GD liegen und die Kapazitäten würden addiert, so dass sich die Grenzfrequenz und Transitfrequenz verringert.

Quelle Vollrath

Nächste Vorlesung

24 Anwendung MOSFET

Kennlinie und MOSFET Parameter Vth, β, λ
MOSFET als Verstärker
MOSFET als Schalter
MOSFET in Leistungsendstufen
MOSFET Ringoszillator
MOSFET Ladungspumpe
MOSFET Spannungsregler
MOSFET Verstärker mit Diodenlast

2020 10 09 23 MOSFET Elektronik Prof. Dr. Joerg Vollrath

Elektronik

23 MOSFET

Prof. Dr. Jörg Vollrath

Video der 23. Vorlesung 11.1.2021

Heute

MOSFET

CMOS Transistoren als Schalter

Typen des Feldeffekttransistors

Die Gleichung des n-Kanal MOSFETs

Wichtige Kenngrößen

Kennlinien:

Übertragungskennlinie

Ausgangskennlinie

Beispiel: NMOSFET-Transistor

Beispiel: MOSFET Bauteil und Kennlinie

MOSFET Parameterextraktion

NMOSFET SPICE Modell

CD4007

SPICE MOS Modell

CD4007

ALD1106, ALD1107

ALD1101, ALD1102

CMOS 1µm models (Holberg)

Transistorentwicklung

MOSFET als Verstärker: Das Prinzip

MOSFET als Verstärker: Die Kennlinie

Großsignalverhalten und Kleinsignalverhalten

Kleinsignalverhalten

Nächste Vorlesung:

Kapazitäten elektronischer Bauelemente

MOSFET Frequenzverhalten

MOSFET Frequenzverhalten

Genauere Rechnung:

MOSFET Frequenzverhalten

Nächste Vorlesung