Elektronik

24 MOSFET

Prof. Dr. Jörg Vollrath

23 MOSFET

Video der 24. Vorlesung 12.1.2021

Länge: 00:00:00

0:0:0 PFET Rechnung

0:2:0 MOSFET als Verstärker

0:3:0 Verstärker und Transistorkennlinie

0:6:0 Kleinsignalverhalten und Spannungsverstärkung

0:9:27 MOSFET Bauteil, Messung und Kennlinie

0:14:0 Messaufbau

0:16:20 Arbeitspunkt bestimmen

0:23:12 Lambda mit Gleichungen 1 und 2 (UGS = konstant)

0:29:13 Nachdenken über die Lösung

0:34:48 Schwellspannung Uth 1 und 3 (UDS = konstant)

0:40:28 KN

0:41:13 Praktische Durchführung

0:44:38 MOSFET als Spannungsverstärker

0:49:35 Schaltungssimulation in LTSPICE

0:56:13 Transistormodell in LTSPICE

0:59:55 Spannungsverstärkung Formeln

1:2:5 MOSFET als Schalter

1:4:54 Stromspitzen beim Schalten, Kapazitätsumladung

1:6:13 Helligkeit mit Pulsweitenmodulation

1:7:58 Leistungsendstufen A-Betrieb

1:11:58 Leistung P = U * I

1:14:34 Effektivwert

1:15:43 Wirkungsgrad

1:18:7 A-Betrieb 25% Wirkungsgrad

1:19:13 B und A-B Betrieb

Heute

MOSFET Parameter
MOSFET Verstärker
- Spannungsverstärkung
- Schalter für eine Leuchtdiode
Wechselspannung, Wechselstrom:
Lautsprecher
MOSFET Endstufen

Beispiel: MOSFET Bauteil und Kennlinie

An einem MOSFET messen Sie bei einer Gate-Sourcespannung von 2V bei U_DS=3V I_DS=4mA und bei U_DS=5V I_DS=4.4mA. Bei U_GS=1.5V und U_DS=3V messen Sie I_DS=1mA.
Berechnen Sie

$\lambda$ , V_th und K_N.

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\frac{I_{DS1}}{I_{DS2}}= \frac{ \left( 1+\lambda U_{DS1} \right)}{\left( 1+\lambda U_{DS2} \right)}$

$\left( 1+\lambda U_{DS2} \right) \frac{I_{DS1}}{I_{DS2}}= 1+\lambda U_{DS1}$

$\lambda \left( U_{DS2} \frac{I_{DS1}}{I_{DS2}} - U_{DS1} \right) = 1- \frac{I_{DS1}}{I_{DS2}}$

$\lambda =\frac{ 1- \frac{I_{DS1}}{I_{DS2}} }{U_{DS2} \frac{I_{DS1}}{I_{DS2}} - U_{DS1}} = \frac{ 1- \frac{4}{4.4} }{5 \frac{4}{4.4} - 3} V^{-1} =\frac{1}{11} \frac{11}{17} V^{-1}$

$=\frac{1}{17}=0.06 V^{-1}$

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\lambda =0.06 V^{-1}$

$\frac{I_{DS1}}{I_{DS3}}= \frac{ \left( U_{GS1}-U_{th} \right)^2}{\left( U_{GS3}-U_{th} \right)^2}$

$\sqrt{\frac{I_{DS1}}{I_{DS3}}}= \frac{ U_{GS1}-U_{th} }{U_{GS3}-U_{th}}$

$\left( U_{GS3}-U_{th} \right) \sqrt{\frac{I_{DS1}}{I_{DS3}}}= U_{GS1}-U_{th}$

$U_{th} \left( 1-\sqrt{\frac{I_{DS1}}{I_{DS3}}} \right) = U_{GS1}- U_{GS3} \sqrt{\frac{I_{DS1}}{I_{DS3}}}$

$U_{th} = \frac {U_{GS1}- U_{GS3} \sqrt{\frac{I_{DS1}}{I_{DS3}}}}{1-\sqrt{\frac{I_{DS1}}{I_{DS3}}}} = \frac{ 2V -1.5V \cdot 2}{1-2}=1V$

3 Gleichungen, 3 Unbekannte. Der Arbeitsbereich bestimmt welche Gleichung man verwenden muss.

U_GS	U_DS	I_DS
2V	3V	4mA
2V	5V	4.4mA
1.5V	3V	1mA

$I_{DS}= \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)$

$\lambda =0.06 V^{-1}$

$U_{th} = 1 V$

$\beta = \frac{\left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right)}{I_{DS}}$

$\beta = \frac{4mA}{\left( 2V-1V \right)^2 \left( 1+0.06 \cdot 3V \right)} = \frac{4}{1.18} \frac{mA}{V^2} = 3.39 \frac{mA}{V^2}$

MOSFET als Spannungsverstärker

Die Eingangsspannung am Gate erzeugt eine Stromänderung IDS, die mit R_D in eine Ausgangsspannung umgesetzt wird.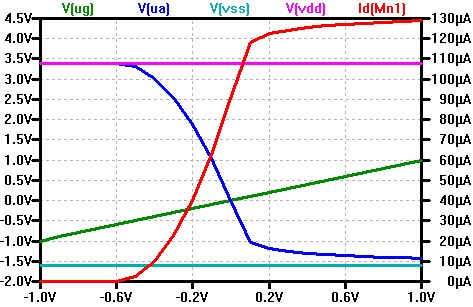

Verstaerker04.asc

Version 4
SHEET 1 888 680
WIRE 256 80 256 64
WIRE 256 176 256 160
WIRE 304 176 256 176
WIRE 256 192 256 176
WIRE 352 240 256 240
WIRE 208 272 176 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 256 304 256 288
FLAG 176 272 UG
FLAG 304 176 UA
FLAG 256 64 VDD
FLAG 256 304 VSS
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMATTR Value CD4007N
SYMBOL res 240 64 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 37.5k
SYMATTR InstName RD
TEXT 120 464 Left 2 !VDD VDD 0 DC 3.4\nVSS VSS 0 DC -1.6\nVGS UG 0 SINE(0 0.05 1k)
TEXT 280 312 Left 2 !.dc VGS -1.0 1.0 0.01
TEXT 112 376 Left 2 !.model CD4007N NMOS(LEVEL=1 \n+ KP=500u VT0=1 LAMBDA=0.002\n+ CGSO=45n CGBO=2n CGDO=45n)
TEXT 144 160 Left 2 !;tran 5m

VSS = -1.6 V, VDD = 3.4 V
Das Schaltbild zeigt die einfachste Spannungsverstärkungsschaltung mit einem MOSFET und einem Widerstand.
Die statische Kennlinie der Schaltung mit den Spannungen und dem Strom wird links gezeigt.
Die rote Kurve zeigt die Änderung des Drain-Source-Stromes mit der Gate-Source-Spannung (Übertragungskennlinie).
Die grüne Kurve zeigt die Eingangsspannung.
Für kleine Eingangsspannungen um 0 V sieht man eine größere invertierte Ausgangsspanungsänderung.
100 mV Amplitude am Eingang (grüne Kurve im Bereich der x-Achse -0.2 V bis 0 V) erzeugt ein invertiertes Signal (blau) mit 1 V Amplitude (y-Achse 2V bis 0V). Eine Spannungsverstärkung v = ua/ue mit dem Faktor 10.
Dies könnte man auch in einer zeitlichen Simulation sehen.

Wie kann man die Spannungsverstärkung ändern?
Warum benötigt man eine negative Spannungsversorgung?

R_D: Bestimmt die Spannungsverstärkung und den Ausgangspegel
Mit VSS kann man den Arbeitspunkt UGS und IDS bestimmen.

MOSFET als Schalter

Der Transistor schaltet die LED an oder aus.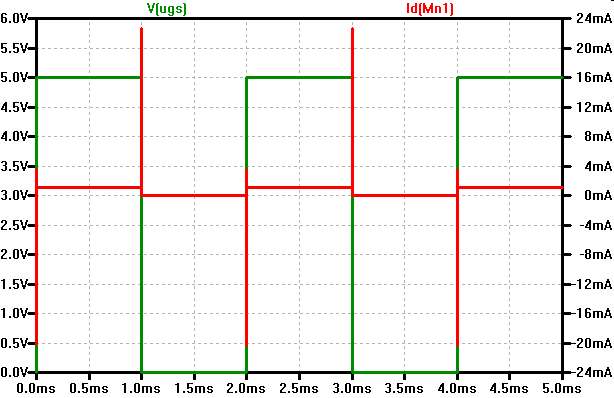

SchalterLED.asc

Version 4
SHEET 1 912 680
WIRE 256 80 256 64
WIRE 256 192 256 144
WIRE 352 240 256 240
WIRE 208 272 176 272
WIRE 352 288 352 240
WIRE 352 288 256 288
WIRE 256 304 256 288
FLAG 176 272 UGS
FLAG 256 64 VDD
FLAG 256 304 0
SYMBOL nmos4 208 192 R0
SYMATTR InstName MN1
SYMATTR Value CD4007N
SYMBOL LED 240 80 R0
SYMATTR InstName D1
SYMATTR Value NSCW100
SYMATTR Description Diode
SYMATTR Type diode
TEXT 120 464 Left 2 !VDD VDD 0 DC 3.4\nVSS VSS 0 DC -1.6\nVGS UGS 0 PULSE(0 5 0 100n 100n 1m 2m)
TEXT 280 312 Left 2 !;dc VGS -1.6 1.6 0.1
TEXT 112 376 Left 2 !.model CD4007N NMOS(LEVEL=1 \n+ KP=500u VT0=1 LAMBDA=0.002\n+ CGSO=45n CGBO=2n CGDO=45n)
TEXT 144 160 Left 2 !.tran 5m

Der Transistors wird nach dem maximalen Strom für die LED bei Betriebsspannung VDD ausgewählt.
Da der Transistor nur ein und ausgeschaltet werden kann, bestimmt man die Helligkeit der LED mit einer Pulsweitenmodulation des Ansteuersignals.
Pulsweitenmodulation: Bei einer hohen Frequenz wird das Verhältnis der Zeit von Transistor an zu Transistor aus variiert.

Bei der Simulation sieht man Stromspitzen, die durch Ladung und Entladung von Kapazitäten entstehen.
Kopplung des Eingangssignals auf den Ausgang auf Grund der Gate-Drain-Kapazität.
Ladung und Entladung der Diodenkapazität.

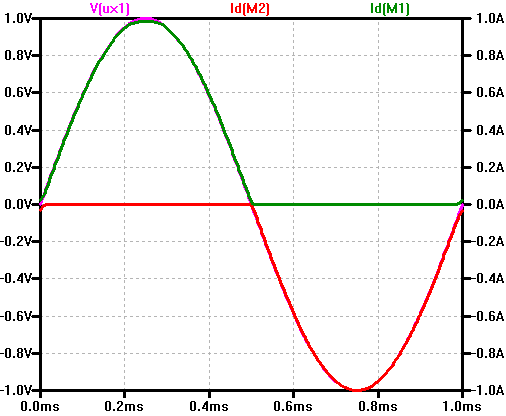
Leistungsendstufen Operationsverstärker AB-Betrieb

Verstärker im AB Betrieb
Niedriger Ausgangswiderstand
Guter Wirkungsgrad
Regelungsschleife mit Opamp
Keine tote Zone, wenig Verzerrungen
Ruhestrom wird durch
VGS2 = - VPP * R2 / (R1+R2)
VGS1 = - VPM * R4 / (R3+R4)
eingestellt.

ClassAB_OpAmpInv.asc

Version 4
SHEET 1 988 680
WIRE 16 -112 -32 -112
WIRE 32 -112 16 -112
WIRE 176 -112 112 -112
WIRE 272 -112 176 -112
WIRE 320 -112 272 -112
WIRE -32 -96 -32 -112
WIRE 272 -64 272 -112
WIRE 272 -64 176 -64
WIRE 16 -32 16 -112
WIRE 80 -32 16 -32
WIRE 128 -32 80 -32
WIRE 176 0 176 -16
WIRE 176 0 -160 0
WIRE 320 0 176 0
WIRE -160 32 -160 0
WIRE -128 32 -160 32
WIRE 320 32 320 0
WIRE -32 48 -32 -16
WIRE -32 48 -64 48
WIRE 128 48 -32 48
WIRE -128 64 -160 64
WIRE 176 64 176 0
WIRE -32 80 -32 48
WIRE 80 80 16 80
WIRE 128 80 80 80
WIRE 272 112 176 112
WIRE 320 128 320 112
WIRE -32 176 -32 160
WIRE 16 176 16 80
WIRE 16 176 -32 176
WIRE 64 176 16 176
WIRE 176 176 176 160
WIRE 176 176 144 176
WIRE 272 176 272 112
WIRE 272 176 176 176
WIRE 320 176 272 176
FLAG 320 -112 VPP
FLAG 320 176 VPM
FLAG 128 48 Ux2
FLAG -160 64 Ux1
FLAG 80 80 Ux2n
FLAG 320 0 UM
FLAG 320 128 0
FLAG 80 -32 Ux2p
SYMBOL nmos4 128 160 M180
WINDOW 3 56 74 Left 2
SYMATTR Value TN0702
SYMATTR InstName M1
SYMBOL OpAmpModel -96 48 M180
SYMATTR InstName X2
SYMATTR SpiceLine R=3 VX = 5
SYMBOL pmos4 128 -112 R0
SYMATTR InstName M2
SYMATTR Value LP0701
SYMBOL res -48 -112 R0
SYMATTR InstName R1
SYMATTR Value 6k
SYMBOL res -48 64 R0
SYMATTR InstName R3
SYMATTR Value 6k
SYMBOL res 128 -128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL res 160 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R4
SYMATTR Value 10k
SYMBOL res 304 16 R0
SYMATTR InstName RL
SYMATTR Value 1
TEXT 408 -16 Left 2 !;dc VAWG1 -2 3 0.05
TEXT 408 -56 Left 2 !.tran 0 10m 1m
TEXT 416 -96 Left 2 !;ac dec 10 1 1000k
TEXT 408 64 Left 2 !VAWG1 Ux1 0 SINE(0 0.5 1k) AC 1\nVPP VPP 0 DC 1.5\nVPM VPM 0 DC -1.5
TEXT 408 32 Left 2 !.include CMOS070.txt

Durch den Operationsverstärker wird eine Rückkoppelung realisiert, so dass das Ausgangssignal dem Eingangssignal folgt.
Dies gleicht die Nichtlinearitäten der Transistoren aus.

Leistungsbetrachtung

$P_{\sin} = \frac{V_{DD}^{2}}{2 \cdot R_{L}}$

$P_{VDD} = \frac{1}{T} \int_0^{T/2} V_{DD} \frac{V_{DD}}{R_{L}} sin( \frac{2 \pi}{T} t) dt$

$P_{VDD} = \frac{1}{T} [ - \frac{V_{DD}^2 T}{2 \pi \cdot R_{L}} cos( \frac{2 \pi}{T} t)]_{0}^{T/2}$

$P_{VDD} = \frac{1}{T} \frac{V_{DD}^2}{R_{L}} \frac{T}{\pi} = \frac{V_{DD}^2}{\pi R_{L}}$

$P_{VDD} = P_{VSS}$

$P_{G} = P_{VSS} + P_{VDD} = \frac{2 \cdot V_{DD}^2}{\pi R_{L}}$

$\eta = \frac{P_{\sin}}{P_{G}} = \frac{\frac{V_{DD}^{2}}{2 \cdot R_{L}}}{\frac{2 \cdot V_{DD}^2}{\pi R_{L}}} = \frac{\pi}{4} = 0.79 = 79 \%$

LTSPICE < ctrl > < left mouseclick >:

Bei sinusförmiger Wechselspannung bestimmt man die mittlere (average) Leistung.

Dabei findet man heraus, dass die mittlere Wechselspannungsleistung einer Gleichspannungsleistung mit einer Gleichspannung

$U_{Gleich} = \frac{\hat{u}_{Wechsel}}{\sqrt{2}}$
und einem Gleichstrom

$I_{Gleich} = \frac{\hat{i}_{Wechsel}}{\sqrt{2}}$
entspricht.

$P = U \cdot I = \frac{\hat{u}}{\sqrt{2}} \cdot \frac{\hat{i}}{\sqrt{2}} = \frac{\hat{u} \cdot \hat{i}}{2}$

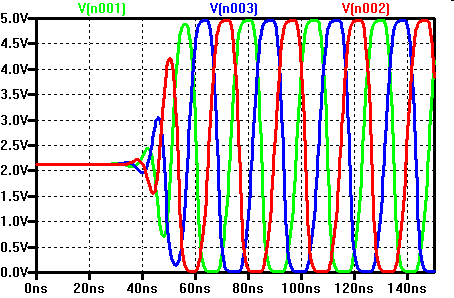
Ringoszillator

Hintereinanderschaltung einer ungeraden Anzahl von Invertern > 1
Inverter sind auch nur Verstärker
Jeder Inverter hat eine Eingangskapazität und einen Ausgangswiderstand.
$\tau = R \cdot C$
Man kann dadurch die Leistung eines Halbleiterherstellungsprozesses bestimmen.

Ring.asc

Version 4
SHEET 1 880 680
WIRE 528 -32 -96 -32
WIRE 16 48 -16 48
WIRE 192 48 160 48
WIRE 384 48 352 48
WIRE -96 144 -96 -32
WIRE -16 144 -16 48
WIRE -16 144 -96 144
WIRE 64 144 64 128
WIRE 160 144 160 48
WIRE 160 144 64 144
WIRE 240 144 240 128
WIRE 352 144 352 48
WIRE 352 144 240 144
WIRE 432 144 432 128
WIRE 528 144 528 -32
WIRE 528 144 432 144
WIRE 576 144 528 144
WIRE 64 160 64 144
WIRE 240 160 240 144
WIRE 432 160 432 144
WIRE 576 160 576 144
WIRE -16 240 -16 144
WIRE 16 240 -16 240
WIRE 160 240 160 144
WIRE 192 240 160 240
WIRE 352 240 352 144
WIRE 384 240 352 240
WIRE 64 272 64 256
WIRE 240 272 240 256
WIRE 432 272 432 256
FLAG 64 272 0
FLAG 64 32 VDD
FLAG 240 272 0
FLAG 240 32 VDD
FLAG 432 272 0
FLAG 432 32 VDD
FLAG 576 240 0
SYMBOL nmos 16 160 R0
SYMATTR InstName M1
SYMATTR Value AO6408
SYMBOL pmos 16 128 M180
SYMATTR InstName M2
SYMATTR Value AO6407
SYMBOL nmos 192 160 R0
SYMATTR InstName M3
SYMATTR Value AO6408
SYMBOL pmos 192 128 M180
SYMATTR InstName M4
SYMATTR Value AO6407
SYMBOL nmos 384 160 R0
SYMATTR InstName M5
SYMATTR Value AO6408
SYMBOL pmos 384 128 M180
SYMATTR InstName M6
SYMATTR Value AO6407
SYMBOL res 560 144 R0
SYMATTR InstName R1
SYMATTR Value 1MEG
TEXT -144 288 Left 2 !VDD VDD 0 5
TEXT 32 320 Left 2 !.tran 0 7.36215m 7.362m 1u

Je höher die Versorgungsspannung ist, desto höher ist die Frequenz und die umgesetzte Leistung.
Bei PCs wird dies genutzt, um mit hoher Spannung höhere Taktfrequenzen zu ermöglichen (Overclocking) oder mit niedriger Spannung die benötigite Leistung zu vermindern (Mobile Geräte).
Die minimale Spannung wird von den Schwellspannungen der Transistoren bestimmt. Die maximale Spannung wird von der Transistorlänge und der Dotierung bestimmt, da sich die Raumladungszonen von Drain und Source zur Verhinderung eines Durchbruchs nicht berühren dürfen.

Ladungspumpe, Pelliconi Charge pump,

MOS Transistor als Schalter: X1, X2, X3, X4
Ladungsspeicher C1, C2
Start: Alle Knoten 0 V.
Phase(1): Phi1 high (VDD), Phi2 low

M1:off, M9:on
M2:on, M8:off
In is charging C2: VDD
Out is connected to C1: VDD

Phase(2): Phi1 low, Phi2 high (VDD)

M1:on, M9:off
M2:off, M8:on
In is charging C1: VDD
Out is connected to C2: 2 VDD

C1,C2: 10 uF
C3: 1 uF

Charge.asc

Version 4
SHEET 1 2324 680
WIRE 1072 16 1072 0
WIRE 1008 32 944 32
WIRE 944 48 944 32
WIRE 1264 64 1184 64
WIRE 960 96 928 96
WIRE 1008 96 1008 32
WIRE 1072 96 1072 80
WIRE 1072 96 1056 96
WIRE 1136 96 1072 96
WIRE 1184 96 1184 64
WIRE 1264 96 1264 64
WIRE 1264 96 1232 96
WIRE 1040 160 1040 144
WIRE 1104 160 1040 160
WIRE 1216 160 1216 144
WIRE 1216 160 1104 160
WIRE 928 176 928 96
WIRE 928 176 896 176
WIRE 1264 176 1264 96
WIRE 1312 176 1264 176
WIRE 1392 176 1312 176
WIRE 1008 208 976 208
WIRE 1072 208 1072 96
WIRE 1072 208 1008 208
WIRE 1152 208 1072 208
WIRE 1312 208 1312 176
WIRE 1408 208 1312 208
WIRE 976 224 976 208
WIRE 1152 224 1152 208
WIRE 1408 224 1408 208
WIRE 928 272 928 176
WIRE 960 272 928 272
WIRE 1104 272 1104 160
WIRE 1104 272 1056 272
WIRE 1136 272 1104 272
WIRE 1264 272 1264 176
WIRE 1264 272 1232 272
WIRE 1104 304 1104 272
WIRE 1312 304 1312 288
WIRE 1408 304 1408 288
WIRE 1408 304 1312 304
WIRE 1184 320 1184 272
WIRE 1264 320 1264 272
WIRE 1264 320 1184 320
WIRE 1312 320 1312 304
WIRE 1008 336 1008 272
WIRE 1104 400 1104 368
FLAG 1008 336 0
FLAG 944 48 0
FLAG 896 176 In
IOPIN 896 176 In
FLAG 1392 176 Out
IOPIN 1392 176 Out
FLAG 1072 0 Phi1
IOPIN 1072 0 In
FLAG 1104 400 Phi2
IOPIN 1104 400 In
FLAG 1312 320 0
FLAG 1104 160 G2
FLAG 1008 208 G1
SYMBOL nmos4 1056 224 R90
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL nmos4 960 144 R270
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M1
SYMBOL pmos4 1232 224 R90
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M8
SYMBOL pmos4 1136 144 R270
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M9
SYMBOL cap 1056 16 R0
SYMATTR InstName C1
SYMATTR Value 10�
SYMBOL cap 1088 304 R0
SYMATTR InstName C2
SYMATTR Value 10�
SYMBOL res 1296 192 R0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL cap 1392 224 R0
SYMATTR InstName C3
SYMATTR Value 1�
TEXT 856 -112 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 1264 -32 Left 2 !VIN IN 0 2\nV1 Phi1 0 PULSE(0 5 0 100u 100u 900u 2000u)\n \nV2 Phi2 0 PULSE(0 5 1000u 100u 100u 900u 2000u)
TEXT 1320 344 Left 2 !.tran 0 60m 0m

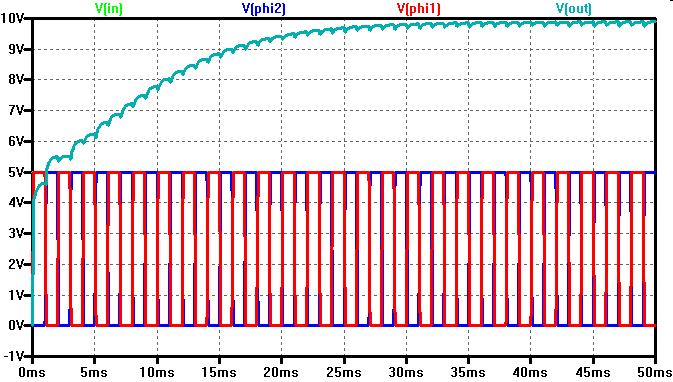
Eine Ladungspumpe kann Spannungen erzeugen, die größer sind als die Versorgungsspannung oder negativ sind. Jede Stufe kann erhöht oder erniedrigt die erzeugte Spannung um eine Versorgungsspannung.
Zum Verständnis der Schaltung führt man die Simulation per Hand durch.
Bei einer Änderung der Spannung an Phi1 wird die Spannungsdifferenz an C1 entsprechend verschoben.
Achtung: Bulk der PFETs muss mit der größten Spannung verbunden sein.

Bei negativen Spannungen wird Eingang und Ausgnag vertauscht und der Bulk Anschluss der NFETs mit der negativsten Spannung verbunden.

ChargeN.asc

Da im idealen Fall die Eingangsleistung gleich der Ausgangsleistung ist, wird bei erhöhter Spannung am Ausgang der Ausgangsstrom entsprechend kleiner.
Dies ist bei der Dimensionierung der Schaltung zu beachten.

Mehrere Stufen

Es dauert einige Zeit bis die Ausgangsspannung erreicht ist.
Ausgangsspannungsschwankungen

Charge3.asc

Version 4
SHEET 1 2776 680
WIRE 1008 32 944 32
WIRE 1584 32 1520 32
WIRE 2144 32 2080 32
WIRE 944 48 944 32
WIRE 1520 48 1520 32
WIRE 2080 48 2080 32
WIRE 1264 64 1184 64
WIRE 1840 64 1760 64
WIRE 2400 64 2320 64
WIRE 960 96 928 96
WIRE 1008 96 1008 32
WIRE 1072 96 1072 80
WIRE 1072 96 1056 96
WIRE 1136 96 1072 96
WIRE 1184 96 1184 64
WIRE 1264 96 1264 64
WIRE 1264 96 1232 96
WIRE 1536 96 1504 96
WIRE 1584 96 1584 32
WIRE 1648 96 1648 80
WIRE 1648 96 1632 96
WIRE 1712 96 1648 96
WIRE 1760 96 1760 64
WIRE 1840 96 1840 64
WIRE 1840 96 1808 96
WIRE 2096 96 2064 96
WIRE 2144 96 2144 32
WIRE 2208 96 2208 80
WIRE 2208 96 2192 96
WIRE 2272 96 2208 96
WIRE 2320 96 2320 64
WIRE 2400 96 2400 64
WIRE 2400 96 2368 96
WIRE 1040 160 1040 144
WIRE 1104 160 1040 160
WIRE 1216 160 1216 144
WIRE 1216 160 1104 160
WIRE 1616 160 1616 144
WIRE 1680 160 1616 160
WIRE 1792 160 1792 144
WIRE 1792 160 1680 160
WIRE 2176 160 2176 144
WIRE 2240 160 2176 160
WIRE 2352 160 2352 144
WIRE 2352 160 2240 160
WIRE 928 176 928 96
WIRE 928 176 896 176
WIRE 1264 176 1264 96
WIRE 1312 176 1264 176
WIRE 1344 176 1312 176
WIRE 1504 176 1504 96
WIRE 1504 176 1344 176
WIRE 1840 176 1840 96
WIRE 1888 176 1840 176
WIRE 1936 176 1888 176
WIRE 2064 176 2064 96
WIRE 2064 176 1936 176
WIRE 2400 176 2400 96
WIRE 2448 176 2400 176
WIRE 2528 176 2448 176
WIRE 1072 208 1072 96
WIRE 1072 208 976 208
WIRE 1152 208 1072 208
WIRE 1312 208 1312 176
WIRE 1408 208 1312 208
WIRE 1648 208 1648 96
WIRE 1648 208 1552 208
WIRE 1728 208 1648 208
WIRE 1888 208 1888 176
WIRE 1984 208 1888 208
WIRE 2208 208 2208 96
WIRE 2208 208 2112 208
WIRE 2288 208 2208 208
WIRE 2448 208 2448 176
WIRE 2544 208 2448 208
WIRE 976 224 976 208
WIRE 1152 224 1152 208
WIRE 1408 224 1408 208
WIRE 1552 224 1552 208
WIRE 1728 224 1728 208
WIRE 1984 224 1984 208
WIRE 2112 224 2112 208
WIRE 2288 224 2288 208
WIRE 2544 224 2544 208
WIRE 928 272 928 176
WIRE 960 272 928 272
WIRE 1104 272 1104 160
WIRE 1104 272 1056 272
WIRE 1136 272 1104 272
WIRE 1264 272 1264 176
WIRE 1264 272 1232 272
WIRE 1504 272 1504 176
WIRE 1536 272 1504 272
WIRE 1680 272 1680 160
WIRE 1680 272 1632 272
WIRE 1712 272 1680 272
WIRE 1840 272 1840 176
WIRE 1840 272 1808 272
WIRE 2064 272 2064 176
WIRE 2096 272 2064 272
WIRE 2240 272 2240 160
WIRE 2240 272 2192 272
WIRE 2272 272 2240 272
WIRE 2400 272 2400 176
WIRE 2400 272 2368 272
WIRE 1104 304 1104 272
WIRE 1312 304 1312 288
WIRE 1408 304 1408 288
WIRE 1408 304 1312 304
WIRE 1680 304 1680 272
WIRE 1888 304 1888 288
WIRE 1984 304 1984 288
WIRE 1984 304 1888 304
WIRE 2240 304 2240 272
WIRE 2448 304 2448 288
WIRE 2544 304 2544 288
WIRE 2544 304 2448 304
WIRE 1184 320 1184 272
WIRE 1264 320 1264 272
WIRE 1264 320 1184 320
WIRE 1312 320 1312 304
WIRE 1760 320 1760 272
WIRE 1840 320 1840 272
WIRE 1840 320 1760 320
WIRE 1888 320 1888 304
WIRE 2320 320 2320 272
WIRE 2400 320 2400 272
WIRE 2400 320 2320 320
WIRE 2448 320 2448 304
WIRE 1008 336 1008 272
WIRE 1584 336 1584 272
WIRE 2144 336 2144 272
FLAG 1008 336 0
FLAG 944 48 0
FLAG 896 176 In
IOPIN 896 176 In
FLAG 1344 176 Out1
FLAG 1072 16 Phi1
IOPIN 1072 16 In
FLAG 1104 368 Phi2
IOPIN 1104 368 In
FLAG 1312 320 0
FLAG 1584 336 0
FLAG 1520 48 0
FLAG 1936 176 Out2
FLAG 1648 16 Phi1
IOPIN 1648 16 In
FLAG 1680 368 Phi2
IOPIN 1680 368 In
FLAG 1888 320 0
FLAG 2144 336 0
FLAG 2080 48 0
FLAG 2528 176 Out3
IOPIN 2528 176 Out
FLAG 2208 16 Phi1
IOPIN 2208 16 In
FLAG 2240 368 Phi2
IOPIN 2240 368 In
FLAG 2448 320 0
SYMBOL nmos4 1056 224 R90
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL nmos4 960 144 R270
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M1
SYMBOL pmos4 1232 224 R90
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M8
SYMBOL pmos4 1136 144 R270
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M9
SYMBOL cap 1056 16 R0
SYMATTR InstName C1
SYMATTR Value 10�
SYMBOL cap 1088 304 R0
SYMATTR InstName C2
SYMATTR Value 10�
SYMBOL res 1296 192 R0
SYMATTR InstName R1
SYMATTR Value 100k
SYMBOL cap 1392 224 R0
SYMATTR InstName C3
SYMATTR Value 1�
SYMBOL nmos4 1632 224 R90
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M3
SYMBOL nmos4 1536 144 R270
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M4
SYMBOL pmos4 1808 224 R90
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M5
SYMBOL pmos4 1712 144 R270
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M6
SYMBOL cap 1632 16 R0
SYMATTR InstName C4
SYMATTR Value 10�
SYMBOL cap 1664 304 R0
SYMATTR InstName C5
SYMATTR Value 10�
SYMBOL res 1872 192 R0
SYMATTR InstName R2
SYMATTR Value 100k
SYMBOL cap 1968 224 R0
SYMATTR InstName C6
SYMATTR Value 1�
SYMBOL nmos4 2192 224 R90
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M7
SYMBOL nmos4 2096 144 R270
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M10
SYMBOL pmos4 2368 224 R90
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M11
SYMBOL pmos4 2272 144 R270
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M12
SYMBOL cap 2192 16 R0
SYMATTR InstName C7
SYMATTR Value 10�
SYMBOL cap 2224 304 R0
SYMATTR InstName C8
SYMATTR Value 10�
SYMBOL res 2432 192 R0
SYMATTR InstName R3
SYMATTR Value 100k
SYMBOL cap 2528 224 R0
SYMATTR InstName C9
SYMATTR Value 1�
TEXT 856 -112 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 856 432 Left 2 !VIN IN 0 5\nV1 Phi1 0 PULSE(0 5 0 100u 100u 900u 2000u)\n\nV2 Phi2 0 PULSE(0 5 1000u 100u 100u 900u 2000u)
TEXT 1320 344 Left 2 !.tran 0 250m 0

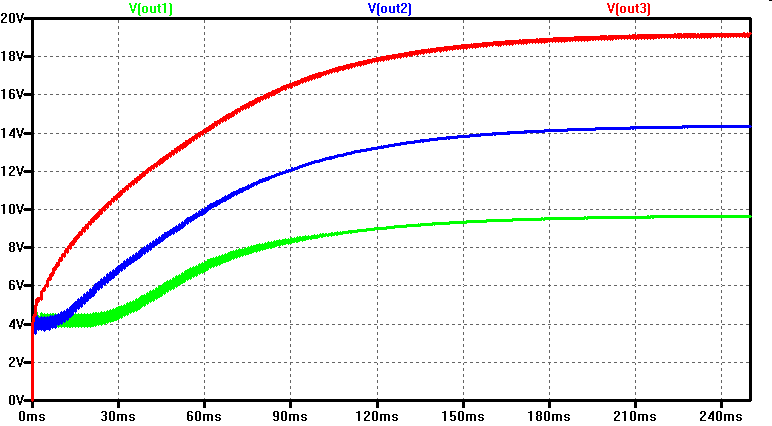
Bei n Stufen ergibt sich eine Spannung von n · VDD.

Praktische Realisierung

Ladungspumpe Ringoszillator

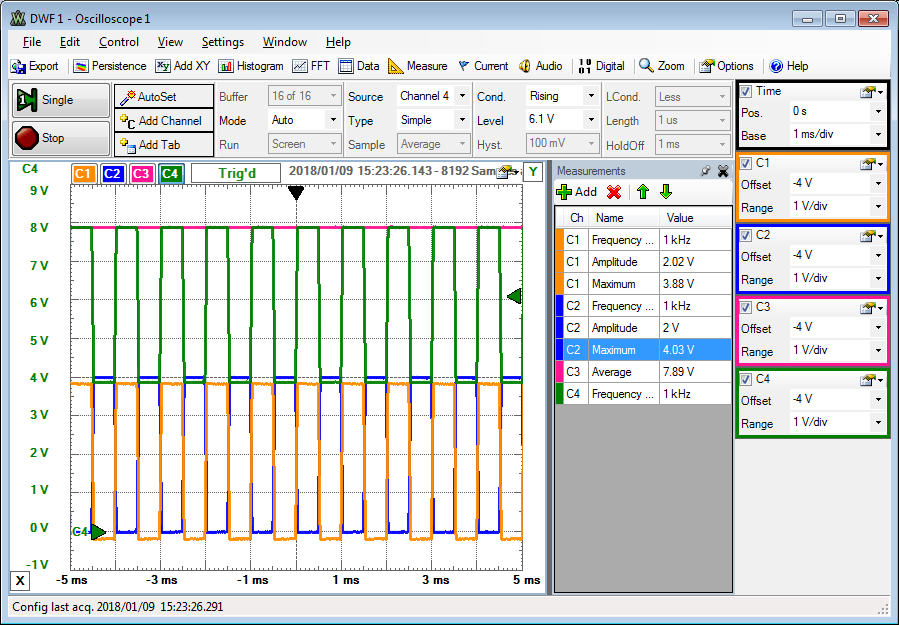
Ringoszillator

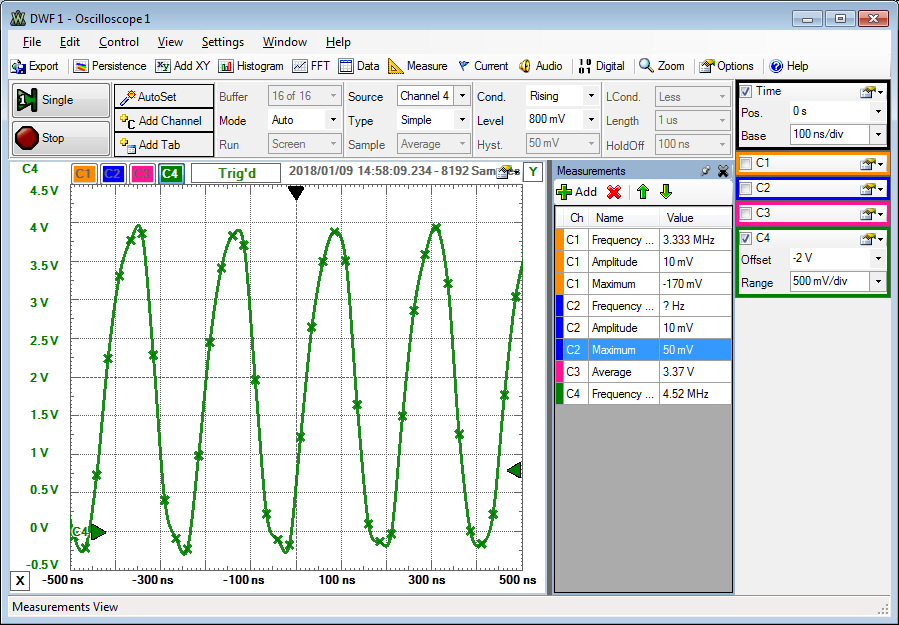
C = 470 nF, f = 1kHz, VDD = 4 V.
Bei der Ladungspumpe wird die Spannung ohne Last von 4 V auf 8 V verdoppelt.
Mit einer Last von 68kΩ reduziert sich die Spannung.

VDD [V]	2	3	4	5	6
f [kHz]	227	2100	4500	6800	8900

Je höher die Spanung, desto größer die Frequenz.

Spannungsregler

Ein Operationsvertärker steuert einen sehr grossen MOSFET (M1) an.
Der Op vergleicht die Ausgangsspannung (U1) mit einer Referenzspannung(Uref).

SpRegler.asc

Version 4
SHEET 1 1132 680
WIRE 32 32 -16 32
WIRE -16 64 -16 32
WIRE 32 112 32 32
WIRE 32 112 -16 112
WIRE -208 128 -240 128
WIRE -64 144 -144 144
WIRE -208 160 -240 160
WIRE -16 176 -16 160
WIRE 80 176 -16 176
WIRE -240 272 -240 160
WIRE -16 272 -16 256
WIRE -16 272 -240 272
WIRE -16 368 -16 352
FLAG 80 176 V1
FLAG -16 32 VDD
FLAG -240 128 Vref
FLAG -16 368 0
SYMBOL res -32 160 R0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL res -32 256 R0
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL pmos4 -64 64 R0
WINDOW 3 57 76 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M1
SYMBOL Opamps\\opamp -176 80 R0
SYMATTR InstName U1
TEXT -248 328 Left 2 !Vref Vref 0 3
TEXT -224 256 Left 2 !.tran 0 2m 0
TEXT -248 296 Left 2 !;dc VDD 4 15 1
TEXT -264 -136 Left 2 !.model CD4007P PMOS(LEVEL=1\n+ KP=200u  VT0=-0.75 \n+ LAMBDA=0.0133 CGDO=400n)\n.include opamp.sub
TEXT -264 -16 Left 2 !VDD VDD 0 SINE( 10 1 10k)

Nächste Vorlesung: Uebung

25 Uebung

Beispiel: Arbeitspunkt einer Transistorschaltung

$Kn = 250 \mu A V^{-2}, Kp = 100 \mu A V^{-2},$

$V_{TN} = 0.6 V, V_{TP} = -0.5 V, V_{DD} = 5V , \lambda = 0.001 V^{-1}.$
Bestimmen Sie die Spannungen

$V_{A}$ und

$V_{B}$ und den Strom

$I_{DSM1}$ .

Transistorgleichung in der Sättigung
Knotengleichung
PFET: Absolutwerte

$\frac{K_{P}}{2} \left( \left|V_{GS3}\right|- |V_{Thp}| \right)^{2} = \frac{K_{N}}{2} \left( V_{GS2}- V_{Thn} \right)^{2} = \frac{K_{N}}{2} \left( V_{GS1}- V_{Thn} \right)^{2}$

$V_{DD} = |V_{GS3}| + V{GS2} + V_{GS}$

$V_{A} = V_{GS1}$ ,

$V_{B} = 2 \cdot V_{A}$

$\frac{K_{P}}{2} \left( V_{DD} - 2 \cdot V_{A} - | V_{Thp}| \right)^{2} = \frac{K_{N}}{2} \left( V_{A}- V_{Thn} \right)^{2}$

$V_{DD} - 2 \cdot V_{A} - | V_{Thp}| = \sqrt{ \frac{K_{N}}{K_{P}}} \left( V_{A}- V_{Thn} \right)$

$V_{A} \left( \sqrt{ \frac{K_{N}}{K_{P}}} + 2 \right) = V_{DD} - | V_{Thp}| + \sqrt{ \frac{K_{N}}{K_{P}} } V_{Thn}$

$V_{A} = \frac{V_{DD} - | V_{Thp}| + \sqrt{ \frac{K_{N}}{K_{P}} } V_{Thn}} { \sqrt{ \frac{K_{N}}{K_{P}}} + 2} = 1.52 V$

$V_{B} = 2 \cdot V_{A} = 3.04 V$ ,

$I_{DS} = \frac{K_{N}}{2} \left( V_{A}- V_{Thn} \right)^{2} = 106\mu A$

MOSArbeit01.asc

Version 4
SHEET 1 1132 680
WIRE 160 -32 160 -48
WIRE 112 -16 96 -16
WIRE 96 80 96 -16
WIRE 160 80 160 64
WIRE 160 80 96 80
WIRE 208 80 160 80
WIRE 96 160 96 80
WIRE 112 160 96 160
WIRE 160 208 160 176
WIRE 160 208 96 208
WIRE 208 208 160 208
WIRE 96 288 96 208
WIRE 112 288 96 288
WIRE 160 320 160 304
FLAG 160 -48 VDD
IOPIN 160 -48 In
FLAG 160 320 0
FLAG 208 208 VA
FLAG 208 80 VB
SYMBOL nmos 112 208 R0
SYMATTR InstName M1
SYMATTR Value CD4007N
SYMBOL nmos 112 80 R0
SYMATTR InstName M2
SYMATTR Value CD4007N
SYMBOL pmos 112 64 M180
SYMATTR InstName M3
SYMATTR Value CD4007P
TEXT 80 -208 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=250u VT0=0.6 LAMBDA=0.001 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=100u VT0=-0.5 LAMBDA=0.001 CGDO=400n)
TEXT 80 -144 Left 2 !VDD VDD 0 5
TEXT 88 -56 Left 2 !.op

Quelle: WS2011_Aufgabe_3.asc

Verstärker Grundschaltungen mit Diodenlast

GrundschaltungenD.asc

Version 4
SHEET 1 1196 708
WIRE 0 128 -144 128
WIRE 32 128 0 128
WIRE 64 128 32 128
WIRE -144 144 -144 128
WIRE 64 176 64 128
WIRE 64 176 0 176
WIRE -48 208 -64 208
WIRE -64 240 -64 208
WIRE 0 240 0 224
WIRE 0 240 -64 240
WIRE 96 240 0 240
WIRE -144 256 -144 224
WIRE -144 256 -160 256
WIRE -80 256 -144 256
WIRE -144 272 -144 256
WIRE 80 288 0 288
WIRE -80 320 -80 256
WIRE -48 320 -80 320
WIRE 0 352 0 336
WIRE 0 352 -144 352
WIRE 80 352 80 288
WIRE 80 352 0 352
WIRE 0 368 0 352
FLAG 0 368 0
FLAG 96 240 UA2
FLAG 32 128 VDDA
FLAG -224 256 UGS
SYMBOL nmos4 -48 240 R0
SYMATTR InstName MN4
SYMATTR Value2 m=4
SYMBOL pmos4 -48 128 R0
SYMATTR InstName M4
SYMATTR Value2 m=1
SYMBOL res -160 128 R0
SYMATTR InstName R4
SYMATTR Value 200k
SYMBOL res -160 256 R0
SYMATTR InstName R5
SYMATTR Value 100k
SYMBOL cap -160 240 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C3
SYMATTR Value 1�
TEXT -368 -8 Left 2 !.model NMOS NMOS(LEVEL=1 KP=500u VT0=1 \n+ LAMBDA=0.002 CGSO=200n CGBO=2n CGDO=200n)\n.model PMOS PMOS(LEVEL=1 KP=500u VT0=-1 \n+ LAMBDA=0.002 CGSO=200n CGBO=2n CGDO=200n)
TEXT -352 320 Left 2 !;tran 0 2.2u 0.2u
TEXT -360 384 Left 2 !.ac oct 10 100 100000k
TEXT -368 104 Left 2 !VE UGS 0 SINE(5 0.1 10000k) AC 1
TEXT -368 352 Left 2 !;dc VE 0 10 0.1
TEXT -344 144 Left 2 !VDDA VDDA 0 10

GrundschaltungenDKESB.asc

Version 4
SHEET 1 880 680
WIRE -32 128 -64 128
WIRE 64 128 -32 128
WIRE 336 128 144 128
WIRE 384 128 336 128
WIRE 432 128 384 128
WIRE 480 128 432 128
WIRE 144 160 144 128
WIRE 336 160 336 128
WIRE 432 160 432 128
WIRE -32 208 -32 128
WIRE 64 208 64 128
WIRE -32 320 -32 288
WIRE 64 320 64 288
WIRE 64 320 -32 320
WIRE 144 320 144 240
WIRE 144 320 64 320
WIRE 336 320 336 240
WIRE 336 320 144 320
WIRE 432 320 432 240
WIRE 432 320 336 320
WIRE 336 336 336 320
FLAG 336 336 0
FLAG -64 128 UGS
IOPIN -64 128 In
FLAG 64 128 UGS
FLAG 384 128 VDS
FLAG 480 128 UA2
IOPIN 480 128 Out
SYMBOL res 48 192 R0
SYMATTR InstName R5
SYMATTR Value 100k
SYMBOL res -48 192 R0
SYMATTR InstName R4
SYMATTR Value 200k
SYMBOL res 416 144 R0
SYMATTR InstName RMP
SYMATTR Value {rmp}
SYMBOL res 320 144 R0
SYMATTR InstName RDN
SYMATTR Value 100k
SYMBOL bi 144 160 R0
SYMATTR InstName B1
SYMATTR Value I={gmn} * V(UGS)
TEXT -40 72 Left 2 !.param gmn=2m rmp=10k
TEXT -120 352 Left 2 !VGS UGS 0 SINE(0 0.5 100k) AC 1
TEXT -120 384 Left 2 !.tran 50u

Der PFET M4 ersetzt den Widerstand. Da Gate und Drain verbunden sind, ist im Kleinsignalersatzschaltbild nur der Ausgangsleitwert g_mp wirksam.
1/g_mp ist normalerweise kleiner als R_dp.
Durch das Größenverhältnis (Stromverhältnis, β )der Transistoren lässt sich die Verstärkung festlegen.
Mit dieser Schaltung lässt sich nur eine niedrige Verstärkung realisieren (< 10).

Die Gatespannung am Transistor M4 wird durch Überlagerung der Gleichspannung VDD und der Eingangsspannung UE erzeugt.

Superposition

Wechselspannungsquelle UE:

$UG1 = \frac{\frac{1}{\frac{1}{R4}+\frac{1}{R4}}} {j \omega C3 + \frac{1}{\frac{1}{R4}+\frac{1}{R4}}} UE$

$UG1 = \frac{1} { j \omega C3 \left( \frac{1}{R4}+\frac{1}{R4} \right) + 1} UE$

Für größere Frequenzen wird damit

$UG1 \approx UE$

Gleichspannungsquelle VDD:

$UG2 = \frac{R5}{R4 + R5} VDD$

$UG = UG1 + UG2 = UE + \frac{R5}{R4 + R5} VDD$

Zur Wechselspannung UE wird eine Gleichspannung UG2 addiert.

Kleinsignalbetrachtung:

$v_u = \frac{u_a}{u_e} = - \frac{u_e \cdot g_{mn4} \cdot \frac{1}{g_{dn4} + g_{mp4}}}{u_e} = - \frac{ g_{mn4} }{g_{dn4} + g_{mp4}} \approx - \frac{ g_{mn4} }{g_{mp4}}$
Großsignalbetrachtung:

$I_{DS} = \beta_{n4} \left( U_{GSN4} - U_{thn} \right)^2 = \beta_{p4} \left( U_{GSP4} - U_{thp} \right)^2$

$\sqrt{\frac{\beta_{n4}}{\beta_{p4}}} \left( U_{E} - U_{thn} \right) = \left( U_{DD} - U_{A} - U_{thp} \right)$

$U_{A} = U_{DD} - U_{thp} + \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{thn} - \sqrt{\frac{\beta_{n4}}{\beta_{p4}}} U_{E}$

Nächste Vorlesung

25 Übung: Diode, MOSFET, Bauteilparameter

2020 10 09 24 MOSFET Elektronik Prof. Dr. Joerg Vollrath

Elektronik

24 MOSFET

Prof. Dr. Jörg Vollrath

Video der 24. Vorlesung 12.1.2021

Heute

Beispiel: MOSFET Bauteil und Kennlinie

MOSFET als Spannungsverstärker

MOSFET als Schalter

Leistungsendstufen Operationsverstärker AB-Betrieb

Leistungsbetrachtung

Ringoszillator

Ladungspumpe, Pelliconi Charge pump,

Mehrere Stufen

Praktische Realisierung

Ringoszillator

Spannungsregler

Nächste Vorlesung: Uebung

Beispiel: Arbeitspunkt einer Transistorschaltung

Verstärker Grundschaltungen mit Diodenlast

Superposition

Nächste Vorlesung