Elektronik

26 Anwendungen

Prof. Dr. Jörg Vollrath

25 Uebung

Video der 26. Vorlesung Übung 19.1.2021

Länge: 00:00:00

0:0:0 Operationsverstärker Übertragungsfunktion

0:0:45 Ansatz Übertragungsfunktion

0:6:3 Gleichspannungsverstärkung

0:8:53 Eingangswiderstand

0:11:13 Komplexe Übertragungsfunktion

0:12:13 Eckfrequenzen

0:23:14 MOSFET Parameter

0:28:3 Arbeitsbereich für die Messungen

0:36:3 Transistorgleichung Sättigung

0:38:11 Uth

0:39:45 Übertragungsfunktion

0:46:37 Lösung

0:47:15 f3dB

0:49:38 Verifikation mit LTSPICE

0:54:31 Frequenzgang

Einweggleichrichter

Spannungsabfall an der Diode
Ohne Glättungskondensator eine positive Halbwelle
Mit Glättungskondensator
Zeitkonstante

$\tau = R_1 \cdot C_1$

Gleich01.asc

Version 4
SHEET 1 880 680
WIRE 96 -112 32 -112
WIRE 384 -112 160 -112
WIRE 32 -16 32 -112
WIRE 96 -16 32 -16
WIRE 192 -16 160 -16
WIRE 288 -16 192 -16
WIRE 384 -16 384 -112
WIRE 32 0 32 -16
WIRE 288 0 288 -16
WIRE 192 16 192 -16
WIRE 32 96 32 80
WIRE 112 96 32 96
WIRE 192 96 112 96
WIRE 288 96 288 64
WIRE 288 96 192 96
WIRE 384 96 384 64
WIRE 384 96 288 96
WIRE 112 112 112 96
FLAG 112 112 0
FLAG 192 -16 URC
FLAG 384 -112 UR
SYMBOL diode 96 0 R270
WINDOW 0 32 32 VTop 2
WINDOW 3 0 32 VBottom 2
SYMATTR InstName D1
SYMBOL res 176 0 R0
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL voltage 32 -16 R0
WINDOW 3 -1 99 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value SINE(0 10 50)
SYMATTR InstName V1
SYMBOL cap 272 0 R0
SYMATTR InstName C1
SYMATTR Value 2m
SYMBOL diode 96 -96 R270
WINDOW 0 32 32 VTop 2
WINDOW 3 0 32 VBottom 2
SYMATTR InstName D2
SYMBOL res 368 -32 R0
SYMATTR InstName R2
SYMATTR Value 100
TEXT 24 152 Left 2 !.tran 0 60m 20m

Graetzschaltung

4 Dioden
2 Diodenspannungen UF Verlust
SPICE funktioniert nur mit realen Dioden.
SPICE Masseverbindung bei dem Generator.
UR und UX bewegen sich in Bezug auf Masse.
Bei Netzspannung liegen sehr hohe Spannungen an den Dioden.

Graetzschaltung.asc

Version 4
SHEET 1 880 680
WIRE 48 -16 0 -16
WIRE 64 -16 48 -16
WIRE 256 -16 160 -16
WIRE 304 -16 256 -16
WIRE 368 -16 304 -16
WIRE 384 -16 368 -16
WIRE 160 0 160 -16
WIRE 256 0 256 -16
WIRE 0 48 0 -16
WIRE 304 48 304 -16
WIRE 384 48 384 -16
WIRE 64 80 64 -16
WIRE 256 80 256 64
WIRE 256 80 64 80
WIRE 160 96 160 64
WIRE 160 96 64 96
WIRE 256 96 256 80
WIRE 64 128 64 96
WIRE 64 128 0 128
WIRE 160 176 160 160
WIRE 256 176 256 160
WIRE 256 176 160 176
WIRE 304 176 304 112
WIRE 304 176 256 176
WIRE 384 176 384 128
WIRE 384 176 304 176
WIRE 0 256 0 128
FLAG 384 176 UR
FLAG 0 256 0
FLAG 368 -16 Ux
FLAG 48 -16 V1
SYMBOL diode 176 160 R180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D1
SYMATTR Value 1N914
SYMBOL diode 272 160 R180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D2
SYMATTR Value 1N914
SYMBOL diode 176 64 R180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D3
SYMATTR Value 1N914
SYMBOL diode 272 64 R180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D4
SYMATTR Value 1N914
SYMBOL voltage 0 32 R0
WINDOW 3 27 175 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
WINDOW 0 22 16 Bottom 2
SYMATTR Value SINE(0 10 50)
SYMATTR InstName V1
SYMBOL res 368 32 R0
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL cap 288 48 R0
SYMATTR InstName C1
SYMATTR Value 1m
TEXT 64 240 Left 2 !.tran 0 240m 200m

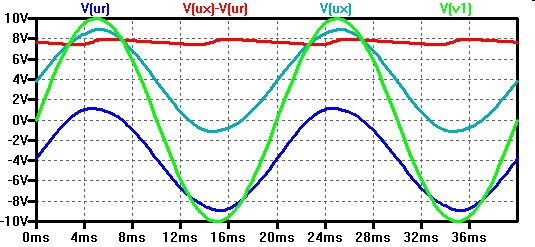Villard Schaltung

C1 und D1 verdoppeln die Spannung des Generators (abzüglich der Vorwärtsspannung U_F)
D2 Trennt den Generator von der Batterie (Entkoppeln)

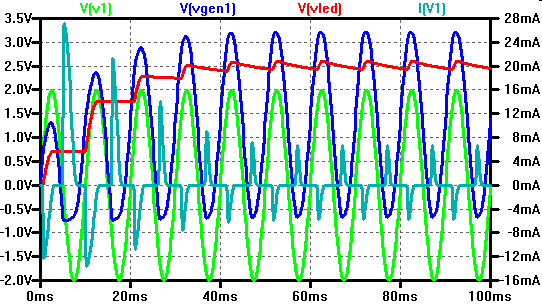Quelle: Vollrath

Villard.asc

Version 4
SHEET 1 880 680
WIRE 96 48 48 48
WIRE 224 48 160 48
WIRE 256 48 224 48
WIRE 336 48 320 48
WIRE 416 48 336 48
WIRE 224 80 224 48
WIRE 336 80 336 48
WIRE 416 80 416 48
WIRE 48 96 48 48
WIRE 48 192 48 176
WIRE 224 192 224 144
WIRE 224 192 48 192
WIRE 288 192 224 192
WIRE 336 192 336 144
WIRE 336 192 288 192
WIRE 416 192 416 144
WIRE 416 192 336 192
WIRE 288 208 288 192
FLAG 288 208 0
FLAG 416 48 vled
FLAG 224 48 vgen1
FLAG 48 48 v1
SYMBOL voltage 48 80 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(0 2 100)
SYMBOL cap 160 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C1
SYMATTR Value 22�
SYMBOL diode 240 144 R180
WINDOW 0 24 72 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D1
SYMATTR Value 1N914
SYMBOL diode 256 32 M90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D2
SYMATTR Value 1N914
SYMBOL cap 320 80 R0
SYMATTR InstName C2
SYMATTR Value 10�
SYMBOL LED 400 80 R0
WINDOW 3 -53 90 Left 2
SYMATTR Value NSPW500BS
SYMATTR InstName D3
SYMATTR Description Diode
SYMATTR Type diode
TEXT 40 224 Left 2 !.tran 0 0.1 0

Man zerlegt die Schaltung in 2 Einweggleichrichterschaltungen.
Die Teilschaltung C1, D1:
Die Spannung

$V_{gen1}$ ist die Summe aus Generatorspannung und einer Kondensatorgleichspannung.

$V_{gen1} = V_{~wechsel} + V_{C}$
Diese pulsierende Gleichspannung wird in der 2.Stufen durch die Diode und den Kondensator geglättet.

Erste positive Halbwelle: C1 und C2 werden mit D2 in Flussrichtung jeweils auf die halbe Versorgungsspannung geladen (C1=C2).
Negative Halbwelle D1 in Flussrichtung lädt C1 auf.

Freilaufdiode

Vermeidung eines Abschaltfunkens oder Zerstörung eines Transistors als Schalter bei induktiver Last.
Das Abschalten führt zu einer Induktionsspannung.
Energie im Magnetfeld
Diode in Durchlassrichtung für die Induktionsspannung.
Wie sehen Strom- und Spannungsverlauf aus?
SPICE:

Freilauf.asc

Version 4
SHEET 1 880 680
WIRE 256 160 -48 160
WIRE 352 160 256 160
WIRE 432 160 352 160
WIRE 256 176 256 160
WIRE 432 176 432 160
WIRE 352 192 352 160
WIRE 160 288 64 288
WIRE -48 304 -48 160
WIRE 256 304 256 256
WIRE 304 304 256 304
WIRE 352 304 352 256
WIRE 352 304 304 304
WIRE 432 304 432 256
WIRE 528 304 432 304
WIRE 64 320 64 288
WIRE 352 352 256 352
WIRE 512 352 432 352
WIRE 160 384 160 288
WIRE 208 384 160 384
WIRE 384 384 208 384
WIRE -48 432 -48 384
WIRE 64 432 64 400
WIRE 64 432 -48 432
WIRE 256 432 256 400
WIRE 256 432 64 432
WIRE 352 432 352 352
WIRE 352 432 256 432
WIRE 432 432 432 400
WIRE 432 432 352 432
WIRE 512 432 512 352
WIRE 512 432 432 432
WIRE 512 448 512 432
FLAG 64 288 vin
FLAG 304 304 mid
FLAG 528 304 mid_no
FLAG 512 448 0
SYMBOL ind 240 160 R0
SYMATTR InstName L1
SYMATTR Value 2m
SYMATTR SpiceLine Rser=10
SYMBOL nmos4 208 304 R0
SYMATTR InstName M1
SYMATTR Value2 l=100u w=100u m=10000
SYMBOL diode 368 256 R180
WINDOW 0 24 72 Left 2
WINDOW 3 -46 -1 Left 2
SYMATTR InstName D1
SYMATTR Value 1N914
SYMBOL ind 416 160 R0
SYMATTR InstName L2
SYMATTR Value 2m
SYMATTR SpiceLine Rser=10
SYMBOL nmos4 384 304 R0
SYMATTR InstName M2
SYMATTR Value2 l=100u w=100u m=10000
SYMBOL voltage 64 304 R0
WINDOW 3 1 154 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value PULSE(0 5 2m 100u 100u 1.9m 4m)
SYMATTR InstName V1
SYMBOL voltage -48 288 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value 12
TEXT -56 488 Left 2 !.tran 0 4.7m 3.7m

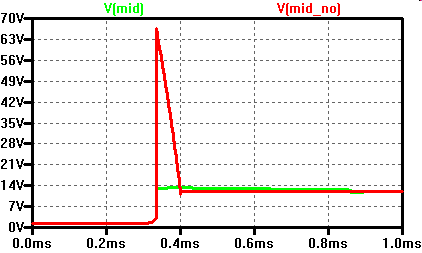Z-Diode: Spannungsbegrenzung

Betrieb im Durchbruch
Dotierung und Geometrie bestimmen die Durchbruchsspannung
Lawinendurchbruch
Maximale Verlustleistung darf nicht überschritten werden.
Temperaturkoeffizient
Positiv
Innenwiderstand im Durchbruchbereich
LTSPICE

zDiode1.asc

Version 4
SHEET 1 880 680
WIRE 128 -16 32 -16
WIRE 256 -16 208 -16
WIRE 32 16 32 -16
WIRE 256 32 256 -16
WIRE 32 112 32 96
WIRE 208 112 32 112
WIRE 256 112 256 96
WIRE 256 112 208 112
WIRE 208 144 208 112
FLAG 208 144 0
FLAG 256 -16 Vout
FLAG 32 -16 Vin
SYMBOL voltage 32 0 R0
WINDOW 3 -22 132 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value SINE(9 2 50)
SYMATTR InstName V1
SYMBOL res 224 -32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1000
SYMBOL zener 272 96 R180
WINDOW 0 24 72 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D1
SYMATTR Value BZX84C6V2L
SYMATTR Description Diode
SYMATTR Type diode
TEXT 8 160 Left 2 !.dc V1 4 8

zDiode2.asc

Version 4
SHEET 1 880 680
WIRE -32 144 -48 144
WIRE 80 144 48 144
WIRE 176 144 160 144
WIRE 16 256 -48 256
WIRE 176 256 80 256
SYMBOL res 176 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RZ1
SYMATTR Value ""
SYMBOL voltage 64 144 R90
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName VZ1
SYMATTR Value ""
SYMBOL zener 16 272 R270
WINDOW 0 36 32 VTop 2
WINDOW 3 -4 32 VBottom 2
SYMATTR InstName D1

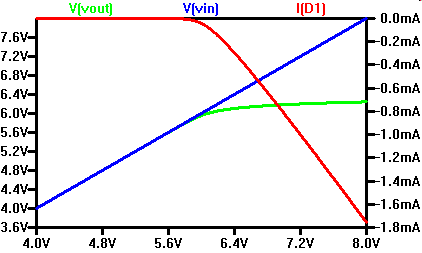Eine Z-Diode wird als Spannungsquelle und Widerstand modelliert.

Z-Diode: Beispiel

Eine Z-Diode mit

$R_Z = 2.8 \Omega$ und

$U_Z = 5.3 V$ wird zur Spannungsstabilisierung an einer Spannungsquelle mit einem Innenwiderstand von

$50 \Omega$ , die zwischen 6V und 8V schwankt eingesetzt. Ein Lastwiderstand von

$5k \Omega$ ist verbunden. Berechnen Sie die minimale und maximale Spannung am Lastwiderstand.

Maschengleichungen und Knotengleichungen
Superposition
Quellenumwandlung
(1)

$U_L = I_2 \cdot R_2$
(2)

$U_L = U_Z + I_Z \cdot R_Z$
(3)

$U_L = U_1 - I_1 \cdot R_1$
(4)

$I_1 = I_2 + I_Z$
in (4) die Ströme durch (1),(2) und (3) ersetzen.

(5)

$\frac{U_1-U_L}{R_1} = \frac{U_L}{R_2} + \frac{U_L-U_Z}{R_Z}$

$(U_1-U_L)R_2R_Z= U_L R_1 R_Z + (U_L-U_Z)R_1 R_2$

$U_L(R_1 R_Z+R_1 R_2+R_2R_Z) = U_1R_2R_Z + U_Z R_1 R_2$

$U_L = \frac{U_1R_2R_Z + U_Z R_1 R_2}{R_1 R_Z+R_1 R_2+R_2R_Z}$

$U_{Lmin} = 5.33 V$

$U_{Lmax} = 5.44 V$
Bei einer Spannungsquellenänderung von 2 V ändert sich die Spannung U_L nur um 0.11 V.

zDiode3.asc

Version 4
SHEET 1 880 680
WIRE 48 32 -16 32
WIRE 176 32 128 32
WIRE 272 32 176 32
WIRE -16 128 -16 32
WIRE 176 128 176 112
WIRE 272 128 272 32
WIRE -16 240 -16 208
WIRE 112 240 -16 240
WIRE 176 240 176 208
WIRE 176 240 112 240
WIRE 272 240 272 208
WIRE 272 240 176 240
WIRE 112 272 112 240
FLAG 112 272 0
FLAG 272 32 UL
FLAG -16 32 U1
SYMBOL voltage -16 112 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(7 1 50)
SYMBOL res 144 16 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 50
SYMBOL res 256 112 R0
SYMATTR InstName R2
SYMATTR Value 5k
SYMBOL res 160 16 R0
SYMATTR InstName RZ
SYMATTR Value 2.8
SYMBOL voltage 176 112 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName VZ
SYMATTR Value 5.3
TEXT -48 272 Left 2 !.tran 100m

Nächste Vorlesung:

27 Musterklausur

2020 10 09 26 Anwendungen Elektronik Prof. Dr. Joerg Vollrath