Elektronik 3

07 Bipolartransistor

Prof. Dr. Jörg Vollrath

06 MOSFET

Elektronik 3 alt Video 12 Bipolartransistor

Länge: 01:06:27

0:0:0 Bipolartransistor

0:1:6 Spitzentransistor

0:5:9 Bipolartransistor Struktur

0:9:34 Animation Struktur und Kennlinien

0:14:23 Bipolartransistor Struktur Folie 5

0:17:20 Vereinfachtes Transportmodell

0:18:36 IC = BN * IB

0:21:14 y=IC, 40=1/UT

0:22:54 AN=IC/IE

0:25:49 Beispiel Bipolartransistor im Normalbetrieb

0:30:16 UCE = VCC - IC * R1 = 8 V

0:32:15 IB = IC/BN = IC (1-AN)/AN = 5,26µA

0:35:36 UBE=0.69 V

0:38:41 Simulation mit min, max Spannungen und Parametern

0:40:0 Early Effekt UEA

0:44:22 Transistoraufbau BCY 591 NPN

0:46:41 Mikroskopbild aufgeschnittener Transistor

0:47:30 Surface mount device (SMD) Gehäuse 1 mm x 2 mm

0:49:58 Bipolar Versuch 06

0:53:59 Messung, Simulation, Gleichung

0:56:12 Bipolar Transistor Messung

0:58:19 Dokumentation einer Messung

1:0:26 Bipolartransistor als Verstärker Kennlinienfelder

1:5:20 Kleinsignalmodell

1:7:49 SPICE Modell Q

1:9:34 Frequenzverhalten

Ziele

Sie können einen Bipolartransistor beschreiben: Anschlüsse, Struktur, Gleichungen, SPICE Modell, Kleinsignalersatzschaltbild
Sie kennen Unterschiede und Gemeinsamkeiten von Bipolartransistor und MOSFET

Spitzentransistor

Walter Brattain
16.Dezember 1947
Spannungsverstärkung 15
Shockley, Bardeen und Brattain: Nobelpreis

Quelle: Wikimedia

Bipolartransistor Struktur

Anschlüsse:

Emitter: E (Bezugspunkt)
Basis: B (Eingang)
Kollektor: C (Ausgang)

Prinzip:

I_C kann durch I_B gesteuert werden.
Geringe Basisweite

Gibt es Ähnlichkeiten zu Feldeffekttransistoren?
Was sind die Unterschiede zu Feldeffekttransistoren?

BipolarT.asc

Version 4
SHEET 1 880 680
WIRE 288 -32 224 -32
WIRE 160 16 112 16
WIRE 224 96 224 64
WIRE 224 96 112 96
WIRE 288 96 224 96
FLAG 288 -32 C
FLAG 112 96 E
FLAG 112 16 B
SYMBOL npn 160 -32 R0
SYMATTR InstName Q2
SYMATTR Value 2N2222
TEXT 8 48 Left 2 ;UBE
TEXT 128 -24 Left 2 ;IB
TEXT 240 -64 Left 2 ;IC
TEXT 128 -24 Left 2 ;IB
TEXT 312 40 Left 2 ;UCE
TEXT 48 160 Left 2 !V1 B 0  0.7
TEXT 48 136 Left 2 !.dc V2 0 10 0.1 V1 0.6 0.7 0.02
TEXT 56 -88 Left 2 ;npn Transistor
TEXT 48 192 Left 2 !V2 C 0 5.0
TEXT 240 160 Left 2 !V3 E 0 0
LINE Normal 80 96 80 16
LINE Normal 80 96 64 80
LINE Normal 96 80 80 96
LINE Normal 144 16 128 0
LINE Normal 128 32 144 16
LINE Normal 272 -16 256 -32
LINE Normal 256 -32 272 -48
LINE Normal 304 80 304 -16
LINE Normal 320 64 304 80
LINE Normal 304 80 288 64

BipolarDioden.asc

Version 4
SHEET 1 880 680
WIRE 192 64 192 32
WIRE 192 144 192 128
WIRE 192 144 128 144
WIRE 192 160 192 144
WIRE 192 256 192 224
FLAG 128 144 B
FLAG 192 256 E
FLAG 192 32 C
SYMBOL diode 176 160 R0
SYMATTR InstName D1
SYMBOL diode 208 128 R180
WINDOW 0 24 64 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName D2

Bipolartransistor Struktur

Ube [V]	Uce [V]
0.7	4.0

Bipolartransistor Struktur

Anschlüsse:

Emitter (Source)
Basis (Gate)
Kollektor (Drain)

Gibt es Ähnlichkeiten zu Feldeffekttransistoren?

3 Anschlüsse

Was sind die Unterschiede zu Feldeffekttransistoren?

Asymmetrie von Kollektor und Emitter
Der Bipolartransistor ist stromgesteuert (I_B signifikant), der MOS Transistor ist Spannungsgesteuert I_G=0.
Herstellung ist komplexer:
Mehr Masken, Isolation, Epitaxie

Quelle: Vollrath

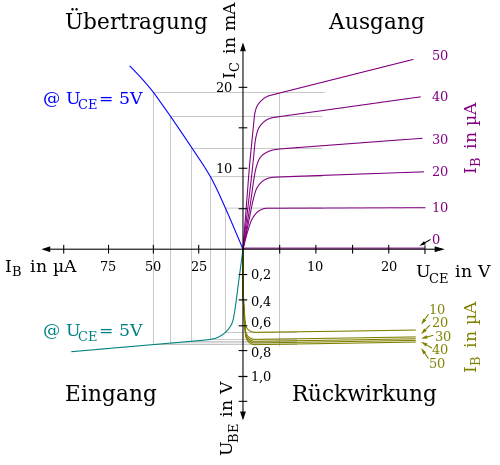
Vereinfachtes Transportmodell im Normalbetrieb

Basis-Kollektor Übergang

Gesperrt

Basis-Emitter Übergang

Durchlassrichtung

Ein kleiner Basis-Emitter Strom steuert einen großen Emitter-Kollektor Strom.
Stromverstärkung:

Emitterschaltung: Emitter ist der gemeinsame Anschluss zwischen Eingang und Ausgang

$B_N =\frac{I_C}{I_B} = \frac{A_N}{1-A_N}=\beta$

Wertebereich: 100..300

$A_N =\frac{I_C}{I_E}=\alpha$

Wertebereich: 0.990..0.997

$I_{C} =B_{N} \cdot I_{B} = I_{S} \cdot e^{\frac{U_{BE}}{U_T}}$

$I_{B} = \frac{I_{C}}{B_{N}} = \frac{I_{S}}{B_{N}} \cdot e^{\frac{U_{BE}}{U_T}}$

$I_{E} = I_{B} +I_{C} = \left( 1 + B_{N} \right) I_{B}$

BipErsatz.asc

Version 4
SHEET 1 880 680
WIRE 256 128 240 128
WIRE 144 176 96 176
WIRE 240 208 240 128
WIRE 144 240 144 176
WIRE 144 336 144 304
WIRE 240 336 240 288
WIRE 240 336 144 336
WIRE 240 384 240 336
WIRE 272 384 240 384
FLAG 96 176 B
FLAG 256 128 C
FLAG 272 384 E
SYMBOL diode 128 240 R0
SYMATTR InstName D2
SYMBOL current 240 208 R0
SYMATTR InstName I2
TEXT 128 144 Left 2 ;IB
TEXT 264 168 Left 2 ;IC
TEXT 264 352 Left 2 ;IE
LINE Normal 128 176 112 160
LINE Normal 112 192 128 176
LINE Normal 240 176 224 160
LINE Normal 256 160 240 176
LINE Normal 240 368 224 352
LINE Normal 256 352 240 368

Quelle: Wikipedia

Der Transistorparameter B_N kann bei der Auftragung I_C über I_B aus der Steigung gewonnen werden.
Der Transistorparameter I_S kann mit einem Messpunkt bestimmt werden.

$I_{S} = \frac{I_{C}}{ e^{\frac{U_{BE}}{U_T}}}$

Beispiel: Bipolartransistor im Normalbetrieb

Beispiel: Berechnen Sie die Spannungen und Ströme folgender Schaltung.
Gegeben:

$I_{S} =10^{-16}A,\alpha_N = 0.95, R_1 = 20 k \Omega$

$V_{CC} = 10 V, I_C = 100 \mu A$

Annahmen: Transportmodell im Normalbetrieb, Raumtemperatur U_T = 25.0 mV

$V_{CE} = V_{CC} - R_1 \cdot I_{C} = 10 V - 100 \mu A \cdot 20 k \Omega = 8V$

$I_{B} = \frac{I_{C}}{B_N} = I_{C} \frac{1 - A_N}{A_N} = 100 \mu A \cdot \frac{0.05}{0.95} = 5.26 \mu A$

$V_{BE} = U_T \cdot \ln \left( \frac{I_{C}}{I_S} \right) = 25 mV \ln \left( \frac{100 \mu A}{10^{-16}A} \right) = 0.69 V$

$I_{E} = I_{C} + I_{B} = 105 \mu A$

Bipolar_B1.asc

Version 4
SHEET 1 880 680
WIRE 432 64 432 48
WIRE 432 176 432 144
WIRE 368 224 320 224
WIRE 432 288 432 272
FLAG 432 288 0
FLAG 432 48 VCC
FLAG 320 224 VBE
SYMBOL npn 368 176 R0
SYMATTR InstName Q1
SYMBOL res 416 48 R0
SYMATTR InstName R1
SYMATTR Value 20k

Bipolartransistor Fragen

Wie heißen die Anschlüsse eines Bipolartransistors?
Welche Gleichungen beschreiben das Verhalten des Bipolartransistors?
Zeichnen Sie einen Querschnitt eines Bipolartransistors

Early Effekt

Leichter Anstieg der Ausgangskennlinie
Veränderung der Basisweite:
Sperrschicht Basis Kollektor

$I_{C} = B_N \cdot I_B \left(1+\frac{U_{CE}}{U_{EA}}\right)$
Early Spannung U_EA

Die Early Spannung U_EA kann bei Messung von 2 Strömen I_C bei gleichem Strom I_B mit 2 Spannungen U_CE aus der Steigung gewonnen werden.

$I_{C1} = B_N \cdot I_B \left(1+\frac{U_{CE1}}{U_{EA}}\right)$

$I_{C2} = B_N \cdot I_B \left(1+\frac{U_{CE2}}{U_{EA}}\right)$

$\frac{I_{C1}}{I_{C2}} = \frac{1+\frac{U_{CE1}}{U_{EA}} }{1+\frac{U_{CE2}}{U_{EA}}}$

$\frac{I_{C1}}{I_{C2}} = \frac{U_{EA}+U_{CE1} }{U_{EA}+U_{CE2}}$

$\frac{I_{C1}}{I_{C2}} \left( U_{EA}+U_{CE2} \right) = U_{EA}+U_{CE1}$

$U_{EA} \left( \frac{I_{C1}}{I_{C2}} - 1 \right) = U_{CE1} - \frac{I_{C1}}{I_{C2}}U_{CE2}$

$U_{EA} = \frac{U_{CE1} - \frac{I_{C1}}{I_{C2}}U_{CE2}}{\frac{I_{C1}}{I_{C2}} - 1}$

Bipolar Transistor BCY 591 NPN

Quelle: Vollrath

Bipolar Transistor Messung

BCY59: NPN
1k Basis AWG1
100 Ohm Collector zu AWG2
AWG1: 750mV+-100mV, 20Hz
AWG2: 3V, 3V, 100Hz

Komplementär BCY79 PNP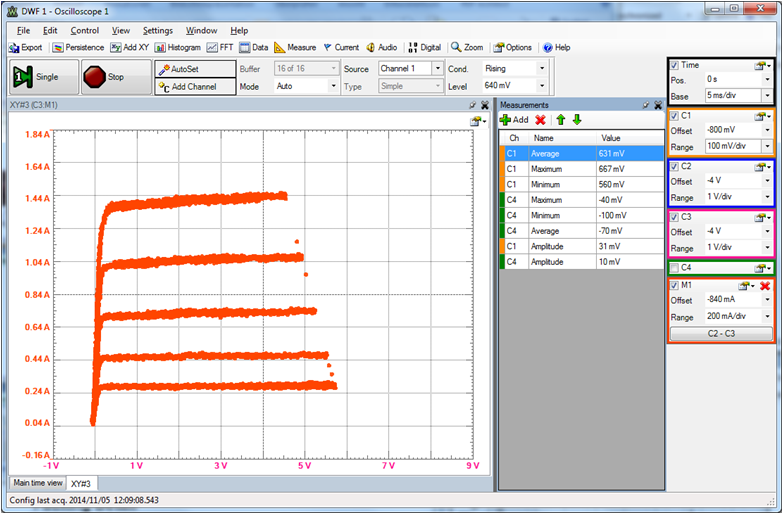
Bipolar Transistor 591 NPN

Quelle: Vollrath

Quelle: Vollrath Bipolar Transistor 591 NPN

Quelle: Vollrath

Die Basis bekommt die Treppenspannung.
Der Kollektor bekommt eine Sinus oder Dreieckspannung.

Bipolartransistor als Verstärker

Kombiniertes Kennlinienfeld Transistor 2

Quelle: Wikipedia Bipolartransistor

Kleinsignalmodell: Hybrid $\pi$ Modell

Linear Näherung für einen Arbeitspunkt Q

Eingangswiderstand

$r_{BE} = \frac{dU_{BE}}{dI_B|_{U_{CE0}}} = \frac{1}{\frac{dI_B}{dU_{BE}}|_{U_{CE0}}}$

$= \frac{1}{\frac{dI_S e^{\frac{U_{BE}}{U_T}}}{dU_{BE}}|_{U_{CE0}}} = \frac{1}{\frac{I_B}{U_T}} = \frac{U_T}{I_B}$

gesteuerte Stromquelle

$\beta i_B = g_m u_{BE} = S \cdot u_{BE}$

$g_m = \frac{\beta i_B}{u_{BE}} = \frac{\beta}{r_{BE}} = \frac{\beta I_B}{U_T} = \frac{I_C}{U_T}$

Ausgangswiderstand

$r_o = \frac{1}{g_d}= \frac{1}{\frac{dI_C}{dU_{CE}}} = \frac{1}{\frac{dI_{S} e^{\frac{U_{BE}}{U_T}} \left(1 + \frac{U_{CE}}{U_{EA}}\right)}{dU_{CE}}} = \frac{U_{EA}}{I_C}$

$I_{C} = I_{S} e^{\frac{U_{BE}}{U_T}} \left(1 + \frac{U_{CE}}{U_{EA}}\right) = \beta I_B \left(1 + \frac{U_{CE}}{U_{EA}}\right)$

BipolarHybPI.asc

Version 4
SHEET 1 880 680
WIRE 32 32 0 32
WIRE 304 32 176 32
WIRE 384 32 304 32
WIRE 32 64 32 32
WIRE 176 64 176 32
WIRE 304 64 304 32
WIRE 32 176 32 144
WIRE 32 176 0 176
WIRE 176 176 176 144
WIRE 176 176 32 176
WIRE 304 176 304 144
WIRE 304 176 176 176
WIRE 384 176 304 176
SYMBOL res 16 48 R0
SYMATTR InstName RBE
SYMATTR Value 1MEG
SYMBOL res 288 48 R0
SYMATTR InstName RCE
SYMATTR Value 100k
SYMBOL current 176 64 R0
SYMATTR InstName I1
SYMATTR Value b IB
TEXT 408 104 Left 2 ;UCE
TEXT -72 112 Left 2 ;UBE
TEXT 8 0 Left 2 ;IB
TEXT 376 8 Left 2 ;IC
LINE Normal 400 160 400 48
LINE Normal 384 144 400 160
LINE Normal 384 144 384 144
LINE Normal 400 160 416 144
LINE Normal -8 168 -8 56
LINE Normal -24 152 -8 168
LINE Normal -40 152 -40 152
LINE Normal -8 168 8 152
LINE Normal 32 32 16 16
LINE Normal 16 48 32 32
LINE Normal 352 32 368 16
LINE Normal 368 48 352 32

SPICE Model Q. Bipolar transistor

Symbol Names: NPN, PNP, NPN2, PNP2

Syntax: Qxxx Collector Base Emitter [Substrate Node] model [area] [off] [IC=] [temp=]

Beispiel:
Q1 C B E MyNPNmodel
.model MyNPNmodel NPN(Bf=75)

Name	Description	Units	Default
I_S	Transport saturation current	A	1E-16
B_f	Ideal maximum forward beta	-	100
V_af	Forward Early voltage	V	infinity
B_r	Ideal maximum reverse beta	-	1

Bipolartransistor LTSPICE Simulation

BipolarVersuchEE.asc

Version 4
SHEET 1 880 680
WIRE 416 -16 384 -16
WIRE 240 16 208 16
WIRE 112 48 96 48
WIRE 240 48 240 16
WIRE 240 48 208 48
WIRE 288 48 240 48
WIRE 416 48 416 -16
WIRE 416 48 368 48
WIRE 208 64 208 48
WIRE 0 112 -80 112
WIRE 112 112 112 48
WIRE 112 112 80 112
WIRE 144 112 112 112
WIRE 416 144 416 48
WIRE -80 160 -80 112
WIRE -80 256 -80 240
WIRE 160 256 -80 256
WIRE 208 256 208 160
WIRE 208 256 160 256
WIRE 416 256 416 224
WIRE 416 256 208 256
WIRE 160 272 160 256
FLAG 160 272 0
FLAG -80 112 SCOPE1DC
FLAG 96 48 SCOPE2DC
FLAG 208 16 SCOPE3DC
FLAG 384 -16 SCOPE4DC
SYMBOL npn 144 64 R0
SYMATTR InstName Q1
SYMATTR Value 2N2222
SYMBOL voltage -80 144 R0
SYMATTR InstName VAWG1
SYMATTR Value 0.6
SYMBOL voltage 416 128 R0
SYMATTR InstName VAWG2
SYMATTR Value 10
SYMBOL res 384 32 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL res 96 96 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R2
SYMATTR Value 10k
TEXT -88 312 Left 0 !.dc VAWG2 0 4 0.1 VAWG1 0.6 0.7 0.025
TEXT 128 136 Left 0 ;B
TEXT 184 184 Left 0 ;E
TEXT 184 48 Left 0 ;C

Quelle: Vollrath

Frequenzverhalten

Datenblatt

$\beta = h_{FE}$	300
$f_{T}$	6 kHz
$f_{g}$	20 Hz

Gain-bandwith product
Verstärkungsbandbreiteprodukt

$f_{T} = \beta \cdot f_{g}$

Quelle Vollrath

Arbeitspunkt und Stromverstärkung

Bei mittleren Strömen maximal

Kleine Ströme
Generations-, Rekombinationsstrom des Basis Emitterübergang steigt an ohne Kollerktorstrom zu beeinflussen.

Große Ströme
Leitfähigkeitserhöhung der Basis
Grössere Raumladungszone zwischen Basis und Kollektor

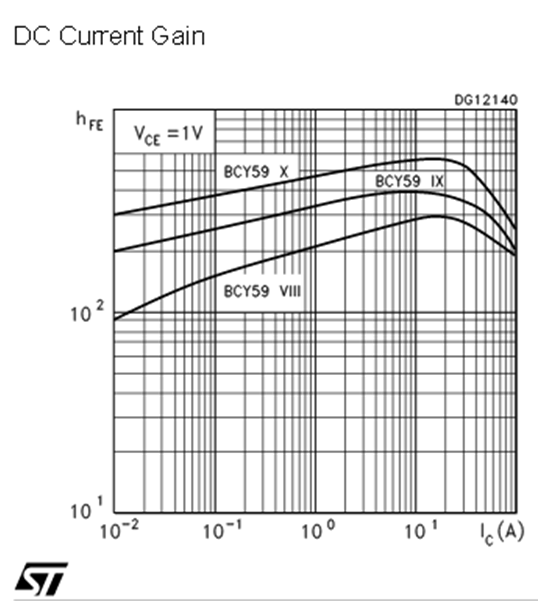Quelle: Datenblatt ST

MOSFET und Bipolartransistor
Kleinsignalparameter und Verstärkung

Bipolartransistor:

$\beta =100, U_{EA}=75V, U_{CE}=10V$

I_C	$g_m = \frac{I_C}{U_T}$	$r_{BE} = \frac{\beta}{g_m}$	$r_o = \frac{U_{EA}}{I_C}$	$\|v_f\| = \frac{U_{EA}}{U_T}$
1uA	40uS	2.5M $\Omega$	75M $\Omega$	3000
10uA	400uS	250k $\Omega$	7.5M $\Omega$	3000
100uA	4mS	25k $\Omega$	750k $\Omega$	3000
1mA	40mS	2.5k $\Omega$	75k $\Omega$	3000
10mA	400mS	0.25k $\Omega$	7.5k $\Omega$	3000

MOSFET:

$KP=1mA/V^2, \lambda =0.0133V^{-1}, U_{DS}=10V$

I_C	$g_m = \sqrt{2 K_P I_D}$	$r_{in} = \infty$	$r_o = \frac{1}{\lambda I_D}$	$\|v_f\| = \frac{1}{\lambda}\sqrt{\frac{2K_P}{I_D}}$	$U_{GS}-U_{th}$
1uA	44.7uS	$\infty$	85.2M $\Omega$	3363	0.04 V
10uA	141uS	$\infty$	8.5M $\Omega$	1063	0.14 V
100uA	447uS	$\infty$	852k $\Omega$	363	0.45 V
1mA	1.41mS	$\infty$	85.2k $\Omega$	106	1.41 V
10mA	4.47mS	$\infty$	8.5k $\Omega$	34	4.47 V

v_f: Spannungsverstärkung in Vorwärtsrichtung (Bipolartransistor)
MOSFET Spannungsverstärkung:

$|v_{f}| = |v_{u}| = \frac{g_{m}}{r_{o}} = \frac{2 I_{D}}{U_{GS}-U_{th}} \frac{1}{\lambda I_{D}}$

$|v_{f}| = \frac{ 2 I_{D }}{\sqrt{\frac{2 I_{D}}{K_{P}}}} \frac{1}{\lambda I_{D}} = \frac{1}{\lambda}\sqrt{\frac{2 K_P}{I_D}}$

Das Verhalten des MOSFETs wird durch das W/L Verhältnis in K_P skaliert.

Diskussion Vergleich MOSFET und Bipolartransistor

Ähnliche Spannungen und für I_C=I_D=1uA ähnliche Spannungsverstärkung
U_BE = 0.7V für alle Bipolartransistoren ( Diodenflussspannung)
U_GS verschieden je nach Schwellspannung U_th
- Bevorzugt Transistor mit Schwellspannung U_th =0.7V
I_D skalierbar mit W/L des Transistors
Spannungsverstärkung nimmt für hohe Ausgangsströme ab.
Ausgangswiderstand abhängig von U_EA, $\lambda$
Eingangswiderstand beim MOSFET $\infty$
Eingangssignale für das Kleinsignalmodell

MOSFET: u_gs < 0.2(U_GS-U_th)
Bipolartransistor: u_be < 0.005V, i_c < 0.2I_C

Nächstes Mal:

08 Rauschen

2023 Elektronik 3 07 Bipolartransistor Prof. Dr. Joerg Vollrath

Elektronik 3

07 Bipolartransistor

Prof. Dr. Jörg Vollrath

Elektronik 3 alt Video 12 Bipolartransistor

Ziele

Spitzentransistor

Bipolartransistor Struktur

Bipolartransistor Struktur

Bipolartransistor Struktur

Vereinfachtes Transportmodell im Normalbetrieb

Beispiel: Bipolartransistor im Normalbetrieb

Bipolartransistor Fragen

Early Effekt

Bipolar Transistor BCY 591 NPN

Bipolar Transistor Messung

Bipolartransistor als Verstärker

Kleinsignalmodell: Hybrid \pi \pi Modell

SPICE Model Q. Bipolar transistor

Bipolartransistor LTSPICE Simulation

Frequenzverhalten

Arbeitspunkt und Stromverstärkung

MOSFET und Bipolartransistor Kleinsignalparameter und Verstärkung

Diskussion Vergleich MOSFET und Bipolartransistor

Nächstes Mal:

Kleinsignalmodell: Hybrid $\pi$ Modell

MOSFET und Bipolartransistor
Kleinsignalparameter und Verstärkung