Elektronik 3

06 MOSFET

Prof. Dr. Jörg Vollrath

05 Diodenschaltungen

Länge: 00:42:10

0:0:0 Bis 9.11.20 Übung 1 Aufgabe 1,2 Übung 2 Aufgabe 3, WS2011 Aufgabe 1; WS2012 Aufgabe 2

0:2:40 Was haben Sie im Praktikum gelernt?

0:4:4 Reflektieren was sie gelernt haben

0:6:50 Abbildung x U Diode, y I Diodenstrom

0:8:18 Ergebnissicherung

0:10:12 Messbereich Oszilloskop Formatfüllende Darstellung

0:12:40 2 Perioden

0:14:25 MOSFET Was nehmen Sie aus der Folie mit?

0:14:57 MOSFET Anschlüsse G, S, D, B

0:17:59 Schaltsymbole

0:19:43 Funktionsprinzip

0:20:59 NFET Kennlinienfeld

0:22:21 Ausgnagskennlinie IDS(UDS) Übertragungskennlinie I(UGS)

0:24:54 Negative Bulkspannung

0:26:54 Drain und Source werden durch angelegte Spannungen definiert

0:28:29 Typen des Feldeffekttransistors

0:31:33 Kennlinien

0:33:10 Vereinfachtes Schaltsymbol

0:34:54 Schalter und Verstärker

0:35:54 Messaufbau für die Kennlinie V4

0:38:48 Gleichung des NFET

0:42:54 3 Parameter Uth, β , λ

0:53:8 Wichtige Kenngrößen, W und L

0:55:39 Schwellspannung

0:57:31 Beispiel NMOS Arbeitsbereich und Strom

1:0:49 Arbeitsbereich Nicht im Sperrbereich

1:2:2 Gleichung für den Strom

1:2:54 1 + λ UDS

1:4:36 Datenblatt Vt, IDS, GOS

1:7:16 Betriebsbereich

1:10:4 PFET Absolutwerte

Elektronik 3 alt Vorlesung und Video Stromspiegel
Elektronik 3 alt Vorlesung und Video Differenzverstärker

Rückblick und Heute

Diode

Spannungsverdopplung
Z-Diode: Spannungsquelle

MOSFET

Physikalische Struktur
Stromspiegel
Differenzverstärker

Elektronische Schaltungstechnik, Reinhold: Kapitel 6, S. 102-124
Microelectronic, Jaeger: Chapter 4, page: 145-216

NFET Kennlinienfeld

Querschnitt eines MOSFET

Ugs [V]	Uds [V]	Ubs [V]
0	0	0

Im Querschnitt des n-Kanal MOSFETs (NFET, NMOS) sieht man in hellgrün die stark n-dotierten (n⁺) Gebiete von Source (S) und Drain (D) in einem schwach p-dotiertem Silizium Wafer (Bulk Kontakt). Diese werden darüber mit Aluminium-Metallkontakten nach oben verbunden (dunkelblau). Zwischen Source und Drain befindet sich das isolierte (grau) Gate (orange, Polysilizium).
Das Isolationsmaterial ist meist SiO₂ (Siliziumoxid, Glas) oder Si₃N₄ (Siliziumnitrid).

Die Animation zeigt, wie sich die Raumladungszone (Source-Bulk, Drain-Bulk, hell orange) und die Ladungsträgerkonzentration (hellgrün) sich bei angelegter Spannung ändert. Dabei wird der gewählte Arbeitspunkt im Kennlinienfeld (oben Ausgangskennlinie, unten Übertragungskennlinie) markiert.

Wie sieht der Querschnitt und das Kennlinienfeld eines PFETS aus?

Die Gleichung des n-Kanal MOSFETs

$I_{DS} = \cases{ 0 & \text{ Sperrbereich } \cr \text{ für } U_{GS} \leq U_{th} \cr \cr \beta \left( U_{GS}-U_{th} \right)^2 \left( 1+\lambda U_{DS} \right) & \text{ Sättigung} \cr \text{ für } 0 \leq U_{GS} - U_{th} \lt U_{DS} \cr \cr \beta \left( 2 \left( U_{GS}-U_{th} \right) U_{DS} - U_{DS}^2 \right) & \text{ Triodenbereich} \cr \text{ für } 0\leq U_{GS} - U_{th} \geq U_{DS} }$

$\beta = \frac{\mu_n \epsilon_{ox}}{2d_{ox}} \frac{W}{L} = \frac{1}{2} \mu_n C_{ox}^{'} \frac{W}{L} = \frac{1}{2} K_{n}^{'} \frac{W}{L} = \frac{1}{2} K_{n} = \frac{1}{2} KP$

U_th : Schwellspannung [V]
β : Steilheitsparameter [A V^-2]
λ : Kanallängenmodulation [V^-1]

Stromspiegel

Einsatz:

Lastelement anstatt eines Widerstandes
Konstantstromquelle

Es soll das Stromverhältnis I2 zu I1 berechnet werden.

Die Transistoren befinden sich in der Sättigung. Es gilt:

$I_{DS} = \beta \left( U_{GS} - U_{Th} \right)^{2} \left( 1 + \lambda U_{DS} \right)$

$U_{GS1} = U_{GS2}$

$\frac{I_2}{I_1} = \frac{\beta_2}{\beta_1} \frac{ \left( 1 + \lambda U_{DS2} \right) }{\left( 1 + \lambda U_{DS1} \right)} = \frac{W_2 \cdot L_1 }{W_{1} \cdot L_{2}} \frac{ \left( 1 + \lambda U_{DS2} \right) }{\left( 1 + \lambda U_{DS1} \right)}$
mit

$L_{1} = L_{2}$

$\frac{I_2}{I_1} \approx \frac{W_{2} }{W_{1}}$

$\lambda$ ist sehr klein.

Man kann mit einem Stromspiegel durch die Wahl eines geeigneten Weitenverhältnisses oder der Anzahl der Transistoren einen Strom verstärken.

Stromspiegel.asc

Version 4
SHEET 1 880 680
WIRE 64 16 64 0
WIRE 64 144 64 96
WIRE 128 144 64 144
WIRE 64 160 64 144
WIRE 240 160 240 0
WIRE 128 240 128 144
WIRE 128 240 112 240
WIRE 160 240 128 240
WIRE 192 240 160 240
WIRE 64 288 64 256
WIRE 240 288 240 256
WIRE 240 288 64 288
WIRE 240 304 240 288
FLAG 240 304 0
FLAG 240 0 VDD
IOPIN 240 0 In
FLAG 160 240 VG
FLAG 64 0 VDD
IOPIN 64 0 In
SYMBOL nmos 192 160 R0
SYMATTR InstName M2
SYMATTR Value NMOS1
SYMBOL nmos 112 160 M0
SYMATTR InstName M1
SYMATTR Value NMOS1
SYMBOL current 64 16 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName I1
SYMATTR Value 1m
TEXT 16 -160 Left 2 !.model NMOS1 NMOS(LEVEL=1\n+ KP=500u  VT0=1 LAMBDA=0.00167\n+ CGSO=1n CGBO=2n CGDO=200n)
TEXT 296 112 Left 2 ;I2
TEXT 80 360 Left 2 !;dc VDD 0 10 0.5
TEXT 0 320 Left 2 !VDD VDD 0 DC 10
TEXT 80 392 Left 2 !.dc I1 1m 5m 1m
LINE Normal 240 128 208 96
LINE Normal 272 96 240 128

Ein Strom I1 durch M1 stellt eine Gate Source Spannung der Transistoren ein und bewirkt einen Stromfluss I2 = I1 im Transistor M2.
Der Strom durch M2 bleibt bei Variation der Spannung VDD nahezu konstant (Stromquelle).

Ausgangswiderstand des Stromspiegels

Bei einer realen Stromquelle interessiert der Innenwiderstand der Quelle.

Ausgangswiderstand von M2

$R_{out} = r_{D}$

Für die Sättigung ist der Ausgangsleitwert definiert als:

$g_d = \frac{d I_{DS}}{d U_{DS}} = \frac{\beta \left( U_{GS} - U_{Th} \right)^{2} \left( 1 + \lambda U_{DS} \right)}{d U_{DS}}$

$g_d = \frac{d I_{DS}}{d U_{DS}} = \beta \left( U_{GS} - U_{Th} \right)^{2} \lambda \approx I_{DS} \lambda$

Der Ausgangswiderstand oder Innenwiderstand einer Stromquelle sollte möglichst groß sein

MOSFET:

$R_{out} = \frac{1}{I_{DS} \lambda}$
Bipolar:

$R_{out} = \frac{U_{EA}}{I_{C}}$

$\frac{1}{ \lambda}$ entspricht

$U_{EA}$

Stromspiegel.asc

Beispiel MOS Stromspiegel

Berechnen Sie den Strom

$I_2$ und den Ausgangswiderstand von folgender Schaltung.

$I_{1} = 150 \mu A, V_{DD} = 10 V,$

$V_{Th} = 1 V, K_{n} = 250 \mu A V^{-2},$

$\lambda = 0.0133 V^{-1}$

$I_{DS} = \frac{K_N}{2} \left( U_{GS} - U_{Th} \right)^{2} \left( 1 + \lambda U_{DS} \right)$
Zur Berechnung des Arbeitspunktes wird der Term

$1 + \lambda U_{DS}$ vernachlässigt.

$U_{GS} = U_{Th} + \sqrt{ \frac{2 \cdot I_{1}}{K_N}} = 1V +\sqrt{\frac{2 \cdot 150 \mu A}{250 \mu A V^{-2}}} = 2.1 V$

$I_2$ unter Berücksichtigung von

$\lambda$

$I_{2} = 150 \mu A \frac{1 + \lambda V_{DD}}{1 + \lambda U_{GS}} = 150 \mu A \frac{1 + 0.0133 \cdot 10 }{1 + 0.0133 \cdot 2.1} = 150 \mu A \frac{1.13}{1.028} = 165 \mu A$
Es gibt eine kleine Stromerhöhung (10%) durch die Spannung

$U_{DS}$ von 10V.

Ausgangswiderstand:

$R_{out} = \frac{1}{I_{DS} \cdot \lambda } = \frac{1}{165 \mu A \cdot 0.0133 V^{-1}} = 456 k \Omega$
Wollte man den Transistor durch einen ohmschen Widerstand ersetzen, benötigt man folgende Spanung:

$U = I_{2} \cdot R_{out} = 165 \mu A \cdot 456 k \Omega = \frac{1}{\lambda} = 75V$

Stromspiegel.asc

Nachdenken über die Lösung

Wann kann man $\left( 1 + \lambda U_{DS} \right)$ vernachlässigen?
Nicht ideales Spiegelverhältnis

$U_{DS}$ ist unterschiedlich

Ausgangswiderstand

äquivalente Spannung $\frac{1}{\lambda }$
Typischer Wert $> 100k \Omega$

Simulation und Demonstration

StromspiegelALD.asc

Version 4
SHEET 1 880 680
WIRE 368 -96 336 -96
WIRE 416 -96 368 -96
WIRE 576 -96 416 -96
WIRE 640 -96 576 -96
WIRE 416 -64 416 -96
WIRE 576 -64 576 -96
WIRE 336 -16 336 -96
WIRE 416 -16 336 -16
WIRE 640 -16 640 -96
WIRE 640 -16 576 -16
WIRE 480 16 464 16
WIRE 528 16 480 16
WIRE 576 48 576 32
WIRE 640 48 576 48
WIRE 416 64 416 32
WIRE 480 64 480 16
WIRE 480 64 416 64
WIRE 576 64 576 48
WIRE 416 96 416 64
WIRE 464 96 416 96
WIRE 576 160 576 144
WIRE 640 160 576 160
WIRE 464 176 416 176
WIRE 416 208 416 176
WIRE 576 208 576 160
WIRE 416 304 416 288
WIRE 576 304 576 288
FLAG 368 -96 VP+
FLAG 416 304 0
FLAG 576 304 0
FLAG 464 96 OSC1
FLAG 640 48 OSC3
FLAG 640 160 OSC4
FLAG 464 176 OSC2
SYMBOL pmos4 528 -64 R0
SYMATTR InstName M3
SYMATTR Value ALD1107P
SYMBOL pmos4 464 -64 M0
SYMATTR InstName M4
SYMATTR Value ALD1107P
SYMBOL res 400 80 R0
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL res 560 48 R0
SYMATTR InstName R2
SYMATTR Value 100
SYMBOL voltage 576 192 R0
SYMATTR InstName VAWG2
SYMATTR Value 0
SYMBOL voltage 416 192 R0
SYMATTR InstName VAWG1
SYMATTR Value 0
TEXT 320 -216 Left 2 !.model ALD1107P PMOS(LEVEL=1\n+ KP=500u  VT0=-1 LAMBDA=0.00167\n+ CGSO=1n CGBO=2n CGDO=200n)
TEXT 424 -128 Left 2 !VP+ VP+ 0 DC 10
TEXT 408 352 Left 2 !.dc VAWG2 -3 3 0.1 VAWG1 0 6 2
TEXT 344 -64 Left 2 ;11
TEXT 448 -80 Left 2 ;3
TEXT 536 -80 Left 2 ;12
TEXT 464 -16 Left 2 ;2
TEXT 504 -16 Left 2 ;13
TEXT 392 40 Left 2 ;1
TEXT 544 40 Left 2 ;14

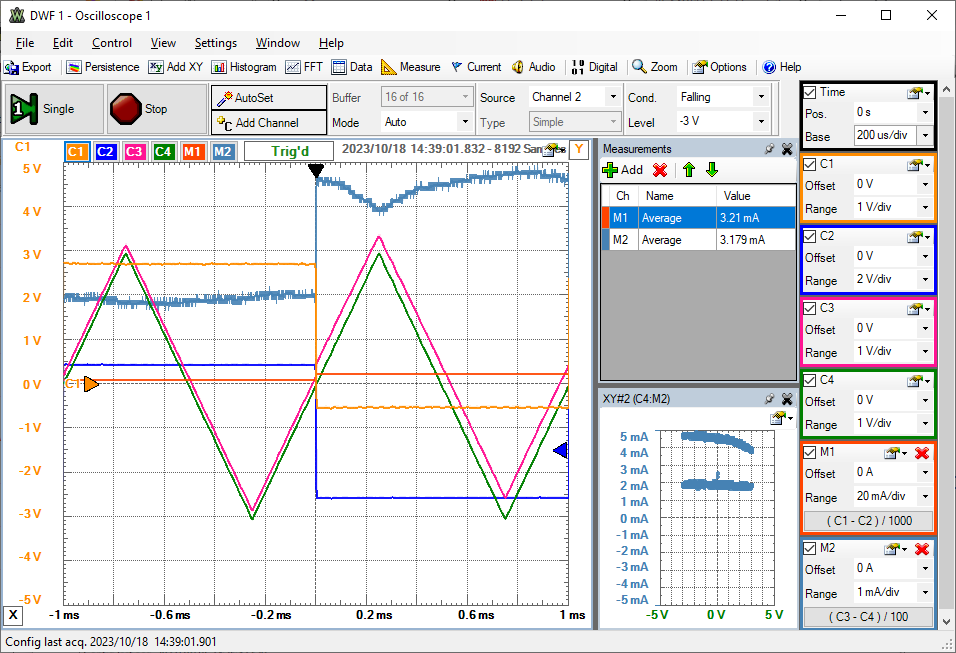
Ein PFET Array ALD1107 wird mit R1 = 1 kOhm und R2 = 100 Ohm verschaltet und mit dem Electronic Explorer betrieben.
Die Versorgungsspannung VP+ = 8V liegt an. Bei grosser Variation der Ausgangsspannung VAWG2 verändert sich der Ausgangsstrom

$I_{R2} = \frac{OSC3 - OSC4}{100}$ wegen des hohen Ausgangswiderstandes kaum.
Man bestimmt mit AWG1 = 1 V, -5 V (Rechtecksignal, f = 500 Hz, Amplitude = 3 V, Offset = -2 V) den Strom I1 (M1) = 2 mA, 4.5 mA und erkennt, dass bei Variation von AWG2 (Triangle, f = 1 kHz, Amplitude = 4 V, Offset = 0 V) von -3 V bis zu +3 V sich der Strom nur wenig ändert.
Die typische Stromquellen Kennlinie ist in der xy Darstellung zu sehen.

Differenzverstärker: Schaltbild

Stromquelle M6 (NFET)
Stromspiegel M4, M5 (PFET)
Eingangstransistoren M2, M7 (NFET)
Gleiche Transistorpaare

M2, M7
M4, M5

Eingang: VA, VB
Ausgang: OUT

Arbeitspunkt: Stromquelle M6
Symmetrische Sourceschaltung

Der Strom verteilt sich hälftig auf M2 und M7

MOSDiff0.asc

Version 4
SHEET 1 1356 680
WIRE 512 -32 416 -32
WIRE 592 -32 512 -32
WIRE 656 -32 592 -32
WIRE 416 -16 416 -32
WIRE 416 -16 368 -16
WIRE 592 -16 592 -32
WIRE 368 32 368 -16
WIRE 416 32 368 32
WIRE 656 32 656 -32
WIRE 656 32 592 32
WIRE 496 64 464 64
WIRE 544 64 496 64
WIRE 416 96 416 80
WIRE 416 96 352 96
WIRE 496 96 496 64
WIRE 496 96 416 96
WIRE 592 96 592 80
WIRE 688 96 592 96
WIRE 416 112 416 96
WIRE 592 112 592 96
WIRE 432 160 416 160
WIRE 592 160 576 160
WIRE 368 192 352 192
WIRE 688 192 640 192
WIRE 432 208 432 160
WIRE 432 208 416 208
WIRE 576 208 576 160
WIRE 592 208 576 208
WIRE 416 256 416 208
WIRE 480 256 416 256
WIRE 512 256 480 256
WIRE 592 256 592 208
WIRE 592 256 512 256
WIRE 496 304 480 304
WIRE 432 336 304 336
WIRE 480 384 480 352
WIRE 496 384 496 304
WIRE 496 384 480 384
WIRE 480 400 480 384
FLAG 480 400 0
FLAG 512 -32 VDD
IOPIN 512 -32 In
FLAG 352 192 VA
IOPIN 352 192 In
FLAG 688 192 VB
IOPIN 688 192 In
FLAG 688 96 OUT
IOPIN 688 96 Out
FLAG 352 96 OUTA
IOPIN 352 96 Out
FLAG 512 256 Vlow
FLAG 304 336 Vref
SYMBOL nmos4 368 112 R0
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL pmos4 464 -16 M0
SYMATTR InstName M4
SYMATTR Value CD4007P
SYMBOL pmos4 544 -16 R0
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M5
SYMBOL nmos4 432 256 R0
WINDOW 3 77 58 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M6
SYMBOL nmos4 640 112 M0
WINDOW 3 -77 121 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M7
TEXT 272 -152 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 312 456 Left 2 !VREF VREF 0 3.33\nVB VB 0 5\nVDD VDD 0 10\nV1 VA 0 SINE(5 0.005 10k) AC 1
TEXT 688 480 Left 2 !.tran 0 0.5m 0
TEXT 688 448 Left 2 !;ac oct 10 1 1MEG
TEXT 536 384 Left 2 ;Differenzverstaerker

Der zweite Eingang des Differenzverstärkers erlaubt die Messung von Differenzen.
Schwankungen der Versorgungsspannung zeigen sich am Ausgang kaum.

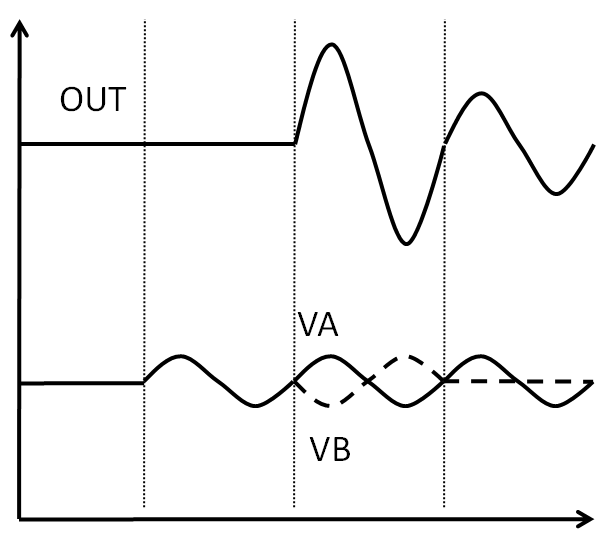
Gegentakt, Differenzverstärker, Signale

MOSDiff1.asc

Version 4
SHEET 1 1356 680
WIRE 512 -32 416 -32
WIRE 592 -32 512 -32
WIRE 656 -32 592 -32
WIRE 416 -16 416 -32
WIRE 416 -16 368 -16
WIRE 592 -16 592 -32
WIRE 368 32 368 -16
WIRE 416 32 368 32
WIRE 656 32 656 -32
WIRE 656 32 592 32
WIRE 496 64 464 64
WIRE 544 64 496 64
WIRE 416 96 416 80
WIRE 416 96 352 96
WIRE 496 96 496 64
WIRE 496 96 416 96
WIRE 592 96 592 80
WIRE 688 96 592 96
WIRE 416 112 416 96
WIRE 592 112 592 96
WIRE 432 160 416 160
WIRE 592 160 576 160
WIRE 368 192 352 192
WIRE 688 192 640 192
WIRE 432 208 432 160
WIRE 432 208 416 208
WIRE 576 208 576 160
WIRE 592 208 576 208
WIRE 416 256 416 208
WIRE 480 256 416 256
WIRE 512 256 480 256
WIRE 592 256 592 208
WIRE 592 256 512 256
WIRE 496 304 480 304
WIRE 432 336 304 336
WIRE 480 384 480 352
WIRE 496 384 496 304
WIRE 496 384 480 384
WIRE 480 400 480 384
FLAG 480 400 0
FLAG 512 -32 VDD
IOPIN 512 -32 In
FLAG 352 192 VA
IOPIN 352 192 In
FLAG 688 192 VB
IOPIN 688 192 In
FLAG 688 96 OUT
IOPIN 688 96 Out
FLAG 352 96 OUTA
IOPIN 352 96 Out
FLAG 512 256 Vlow
FLAG 304 336 Vref
SYMBOL nmos4 368 112 R0
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL pmos4 464 -16 M0
SYMATTR InstName M4
SYMATTR Value CD4007P
SYMBOL pmos4 544 -16 R0
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M5
SYMBOL nmos4 432 256 R0
WINDOW 3 77 58 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M6
SYMBOL nmos4 640 112 M0
WINDOW 3 -77 121 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M7
TEXT 272 -152 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 312 456 Left 2 !VREF VREF 0 3.33\nVB VB 0 5\nVDD VDD 0 10\nVA VA 0 SINE(5 0.005 10k) AC 1
TEXT 688 480 Left 2 !;tran 0 0.5m 0
TEXT 688 448 Left 2 !;ac oct 10 1 1MEG
TEXT 536 384 Left 2 ;Differenzverstaerker
TEXT 688 512 Left 2 !.dc VA 0 10 0.01 VB 0 10 2

Eingangssignal:

Gleichtakt:

$u_{gl} = \frac{u_A + u_B }{2}$

Gegentakt, Differenz:

$u_D = u_A - u_B$

Direkte Einkopplung, keine Koppelkapazität, Gleichspannungsverstärkung
Bei 2 Eingängen kann man das Eingangssignal in einen Gleichtaktsignal und ein Gegentaktsignal zerlegen.
Idealerweise hat der Verstärker eine große Gegentaktverstärkung und keine Gleichtaktverstärkung.
Idealerweise wirkt sich eine Versorgungsspannungsänderung nicht auf das Ausgangssignal aus.
Im Allgemeinen spricht man von single ended und differentiellen (differential) Signalen.
Differentielle Signale sind nicht so störanfällig, da sich Störungen auf beide Signalleitungen auswirken und nachfolgende Differenzverstärker mit geringer Gleichtaktverstärkung diese Störungen unterdrücken.

Funktionsweise des Differenzverstärkers

M6 ist ein Stromspiegeltransistor und stellt den Arbeitspunkt der Schaltung I_DS ein.
Mit I_DS wird über g_m und r_D die Verstärkung und die Leistungsaufnahme festgelegt.
u_a liegt am positiven Eingang
Eine Änderung von u_a bewirkt eine Änderung von der Spannung outa, die die Sourceschaltung aus M5 (Verstärker) und M7 (Last) ansteuert.
Eine positive Änderung von u_a bewirkt eine positive Änderung der Ausgangsspannnung.
u_b liegt am negativem Eingang, an der Sourceschaltung aus M7 (Verstärker) und M5 (Last).
Am Ausgang ergibt sich dadurch die verstärkte Differenzspannung:
u_D = k ( u_a - u_b)

Es wird als nächstes das Kleinsignalersatzschaltbild erstellt und die Gegentakt- und Gleichtaktverstärkung berechnet.

MOSDiff2.asc

Version 4
SHEET 1 1356 680
WIRE 512 -32 416 -32
WIRE 592 -32 512 -32
WIRE 656 -32 592 -32
WIRE 416 -16 416 -32
WIRE 416 -16 368 -16
WIRE 592 -16 592 -32
WIRE 368 32 368 -16
WIRE 416 32 368 32
WIRE 656 32 656 -32
WIRE 656 32 592 32
WIRE 496 64 464 64
WIRE 544 64 496 64
WIRE 416 96 416 80
WIRE 416 96 352 96
WIRE 496 96 496 64
WIRE 496 96 416 96
WIRE 592 96 592 80
WIRE 688 96 592 96
WIRE 416 112 416 96
WIRE 592 112 592 96
WIRE 432 160 416 160
WIRE 592 160 576 160
WIRE 368 192 352 192
WIRE 688 192 640 192
WIRE 432 208 432 160
WIRE 432 208 416 208
WIRE 576 208 576 160
WIRE 592 208 576 208
WIRE 416 256 416 208
WIRE 480 256 416 256
WIRE 512 256 480 256
WIRE 592 256 592 208
WIRE 592 256 512 256
WIRE 496 304 480 304
WIRE 432 336 304 336
WIRE 480 384 480 352
WIRE 496 384 496 304
WIRE 496 384 480 384
WIRE 480 400 480 384
FLAG 480 400 0
FLAG 512 -32 VDD
IOPIN 512 -32 In
FLAG 352 192 VA
IOPIN 352 192 In
FLAG 688 192 VB
IOPIN 688 192 In
FLAG 688 96 OUT
IOPIN 688 96 Out
FLAG 352 96 OUTA
IOPIN 352 96 Out
FLAG 512 256 Vlow
FLAG 304 336 Vref
SYMBOL nmos4 368 112 R0
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL pmos4 464 -16 M0
SYMATTR InstName M4
SYMATTR Value CD4007P
SYMBOL pmos4 544 -16 R0
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M5
SYMBOL nmos4 432 256 R0
WINDOW 3 77 58 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M6
SYMBOL nmos4 640 112 M0
WINDOW 3 -77 121 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M7
TEXT 272 -152 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 312 456 Left 2 !VREF VREF 0 3.33\nVB VB 0 5\nVDD VDD 0 10\nV1 VA 0 SINE(5 0.005 10k) AC 1
TEXT 688 480 Left 2 !.tran 0 0.5m 0
TEXT 688 448 Left 2 !;ac oct 10 1 1MEG
TEXT 536 384 Left 2 ;Differenzverstaerker

Differenzverstärker Simulation und Demonstration

DiffAmpALD.asc

Version 4
SHEET 1 1820 680
WIRE 416 -80 352 -80
WIRE 512 -80 416 -80
WIRE 592 -80 512 -80
WIRE 656 -80 592 -80
WIRE 416 -64 416 -80
WIRE 592 -64 592 -80
WIRE 352 -16 352 -80
WIRE 416 -16 352 -16
WIRE 656 -16 656 -80
WIRE 656 -16 592 -16
WIRE 496 16 464 16
WIRE 544 16 496 16
WIRE 416 64 416 32
WIRE 416 64 336 64
WIRE 496 64 496 16
WIRE 496 64 416 64
WIRE 592 96 592 32
WIRE 688 96 592 96
WIRE 416 112 416 64
WIRE 592 112 592 96
WIRE 432 160 416 160
WIRE 592 160 576 160
WIRE 368 192 352 192
WIRE 688 192 640 192
WIRE 432 208 432 160
WIRE 432 208 416 208
WIRE 576 208 576 160
WIRE 592 208 576 208
WIRE 416 256 416 208
WIRE 480 256 416 256
WIRE 512 256 480 256
WIRE 592 256 592 208
WIRE 592 256 512 256
WIRE 496 304 480 304
WIRE 432 336 304 336
WIRE 480 384 480 352
WIRE 496 384 496 304
WIRE 496 384 480 384
WIRE 480 400 480 384
FLAG 480 400 0
FLAG 512 -80 VDD
IOPIN 512 -80 In
FLAG 352 192 VAAWG2
IOPIN 352 192 In
FLAG 688 192 VBAWG1
IOPIN 688 192 In
FLAG 688 96 OUT
IOPIN 688 96 Out
FLAG 336 64 OUTA
IOPIN 336 64 Out
FLAG 512 256 Vlow
FLAG 304 336 Vref1
SYMBOL nmos4 368 112 R0
WINDOW 3 83 72 Left 2
SYMATTR Value ALD1106N
SYMATTR InstName M1N
SYMBOL pmos4 464 -64 M0
SYMATTR InstName M4P
SYMATTR Value ALD1107P
SYMBOL pmos4 544 -64 R0
WINDOW 3 56 73 Left 2
SYMATTR Value ALD1107P
SYMATTR InstName M3P
SYMBOL nmos4 432 256 R0
WINDOW 3 77 58 Left 2
SYMATTR Value ALD1106N
SYMATTR InstName M4N
SYMBOL nmos4 640 112 M0
WINDOW 3 -77 121 Left 2
SYMATTR Value ALD1106N
SYMATTR InstName M2N
TEXT 720 -104 Left 2 !.model ALD1106N NMOS(LEVEL=1 \n+KP=1123u VT0=1.48 LAMBDA=0.018 \n+CGDO=400n)\n.model ALD1107P PMOS(LEVEL=1 \n+KP=1123u VT0=-1.48 LAMBDA=0.018 \n+CGDO=400n)
TEXT 736 232 Left 2 !VREF1 VREF1 0 3.33\nVB VBAWG1 0 5\nVDD VDD 0 10\nV1 VAAWG2 0 SINE(5 0.005 10k) AC 1
TEXT 720 160 Left 2 !.tran 0 0.5m 0
TEXT 720 136 Left 2 !;ac oct 10 1 1MEG
TEXT 536 384 Left 2 ;Differenzverstaerker
TEXT 352 168 Left 2 ;2
TEXT 384 232 Left 2 ;3
TEXT 448 240 Left 2 ;5
TEXT 560 232 Left 2 ;12
TEXT 648 168 Left 2 ;13
TEXT 384 320 Left 2 ;6
TEXT 456 368 Left 2 ;7
TEXT 560 104 Left 2 ;14
TEXT 560 40 Left 2 ;10
TEXT 392 104 Left 2 ;1
TEXT 520 32 Left 2 ;9
TEXT 464 32 Left 2 ;6
TEXT 392 32 Left 2 ;5
TEXT 416 -104 Left 2 ;7
TEXT 584 -104 Left 2 ;8
TEXT 768 88 Left 2 ;OSC1
TEXT 824 184 Left 2 ;OSC2
TEXT 272 232 Left 2 ;OSC4
TEXT 272 104 Left 2 ;OSC3

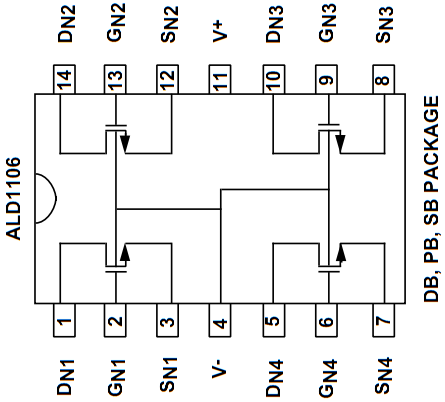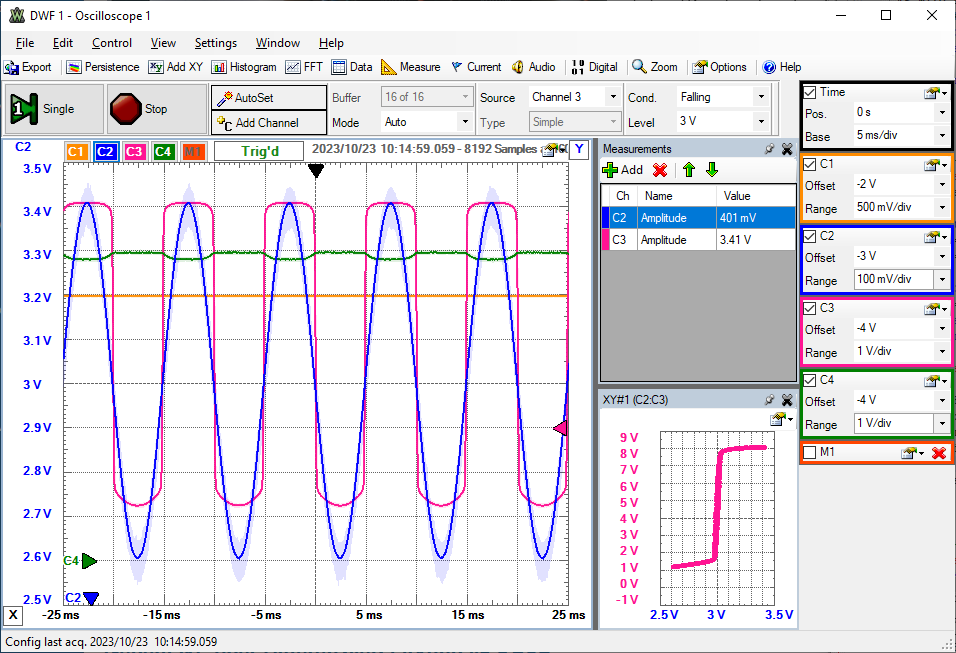
Ein PFET Array ALD1107 und NFET Array ALD1106 wird als Differenzverstärker verschaltet und mit dem Electronic Explorer betrieben.
Die Versorgungsspannung VP+ = 8V und die Referenzspannung Vref1 = 1.4 V liegt an. Bei einer Spannung VAWG1 = 3 V (Offset, 0V Amplitude) wird die Spannungsquelle VAWG2 mit einem Sinussignal (Offset = 3 V, Amplitude = 400 mV) betrieben.
Am Oszilloskop sieht man in blau (C2) die Eingangsspannung VAWG2 mit 400 mV Amplitude, die Spannung OUTA (grün, C4) und die verstärkte Spannung OUT (pink, C3).
In einer x-y Darstellung von C3 über C1 kann man die Übertragungskennlinie sehen und eine Verstärkung von vdiff = dC3/dC2 = 4V / 10mV = 400 ablesen.
Folgende weitere Untersuchungen sind interessant:
1) Variation von Vref1: Wie ändert sich der Strom und die Spannungsverstärkung?
Bei kleinerem Vref nimmt die Verstärkung zu, aber man sieht auch eine Hysterese, bedingt durch eine Phasenverschiebung bei kleinerer Eckfrequenz.
2) Gleichtaktverstärkung: Beide Eingänge werden mit AWG2 betrieben.
vgl = d C3 / d C2 = 35 mV / 400 mV = 0.09
Berechnung der Common mode rejection rate.
CMRR = 20 log (vdiff / vgl ) = 20 log (400 / 0.09 ) = 72 dB
3) Power supply rejection rate: PSRR.
Signal an der Betriebsspannung: d VP+ (C1) = 100 mV; d Vout = 100 mV;
vb = d VP+ / dVout = 1
PSRR = 20 log(vdiff/ vb) = 20 log(400 / 1) = 52 dB
4) Frequenzgang
Wie ändert sich die Verstärkung bei verschiedenen Frequenzen?

Gegentakt- oder Differenzverstärkung v_D KESB

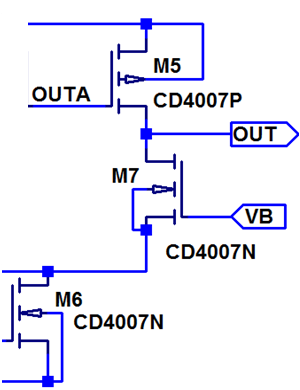
Das Bild zeigt das Kleinsignalersatzschaltbild in LTSPICE.
Berechnung der Differenzverstärkung:

$u_{out} = - \left( i_5 + i_7 \right) \cdot \left( r_{d5} || r_{d7} \right)$

$u_{out} = - \left( u_{outa} \cdot g_{m5} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right)$

$u_{out} = - \left( - u_{a} \cdot g_{m2} \left( r_{D2} || r_{m4} \right) \cdot g_{m5} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right)$
Näherung

$r_{m4} \ll r_{D2}$

$u_{out} \approx - \left( - u_{a} \cdot g_{m2} \frac{g_{m5}}{g_{m4}} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right)$
Mit

$g_{m5} = g_{m4}$ und

$g_{m7} = g_{m2}$ und

$r_{d5} = r_{d7}$

$u_{out} \approx \left( u_{a} - u_{b} \right) \frac{ r_{d7} \cdot g_{m7} }{2}$

MOSDiffE.asc

Version 4
SHEET 1 1356 680
WIRE 416 -64 336 -64
WIRE 688 -64 416 -64
WIRE 768 -64 688 -64
WIRE 416 -48 416 -64
WIRE 336 -32 336 -64
WIRE 688 -32 688 -64
WIRE 768 -32 768 -64
WIRE 336 64 336 48
WIRE 416 64 336 64
WIRE 688 64 688 48
WIRE 688 64 592 64
WIRE 768 64 768 48
WIRE 768 64 688 64
WIRE 592 96 592 64
WIRE 656 96 592 96
WIRE 224 128 208 128
WIRE 336 128 336 64
WIRE 336 128 272 128
WIRE 448 128 336 128
WIRE 592 128 592 96
WIRE 592 128 560 128
WIRE 688 128 592 128
WIRE 784 128 752 128
WIRE 272 144 272 128
WIRE 448 144 448 128
WIRE 560 144 560 128
WIRE 688 144 688 128
WIRE 272 256 272 224
WIRE 448 256 448 224
WIRE 448 256 272 256
WIRE 496 256 448 256
WIRE 512 256 496 256
WIRE 560 256 560 224
WIRE 560 256 512 256
WIRE 688 256 688 224
WIRE 688 256 560 256
WIRE 496 352 496 256
FLAG 208 128 VA
IOPIN 208 128 In
FLAG 784 128 VB
IOPIN 784 128 In
FLAG 656 96 OUT
IOPIN 656 96 Out
FLAG 416 64 OUTA
FLAG 512 256 Vlow
FLAG 416 -48 0
FLAG 496 352 0
SYMBOL bi 272 144 R0
SYMATTR InstName B2
SYMATTR Value I={gm}*V(VA)
SYMBOL res 432 128 R0
SYMATTR InstName RD2
SYMATTR Value {rd}
SYMBOL res 544 128 R0
SYMATTR InstName RD7
SYMATTR Value {rd}
SYMBOL bi 688 144 R0
SYMATTR InstName B7
SYMATTR Value I={gm}*V(VB)
SYMBOL res 320 -48 R0
SYMATTR InstName RM4
SYMATTR Value {1/gm}
SYMBOL bi 688 48 R180
WINDOW 0 24 80 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName B5
SYMATTR Value I={gm}*V(OUTA)
SYMBOL res 752 -48 R0
SYMATTR InstName RD5
SYMATTR Value {rd}
TEXT 216 -176 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u \n+ VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u \n+VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 208 368 Left 2 !VREF VREF 0 3.33\nVB VB 0 SINE(0 0.005 10k) AC 1\nVDD VDD 0 10\nV1 VA 0 SINE(0 0.005 10k 0 0 180) AC 1
TEXT 648 392 Left 2 !.tran 0 0.5m 0
TEXT 648 368 Left 2 !;ac oct 10 1 1MEG
TEXT 528 312 Left 2 ;Differenzverstaerker
TEXT 208 104 Left 2 ;G2
TEXT 752 112 Left 2 ;G7
TEXT 288 280 Left 2 ;S
TEXT 608 272 Left 2 ;S
TEXT 720 -80 Left 2 ;S
TEXT 656 424 Left 2 !.param gm=1m\n.param rd=1/10u

MOSDiffE1.asc

Version 4
SHEET 1 1356 680
WIRE 432 64 400 64
WIRE 48 128 32 128
WIRE 272 128 96 128
WIRE 368 128 272 128
WIRE 416 128 368 128
WIRE 768 128 560 128
WIRE 928 128 768 128
WIRE 1024 128 928 128
WIRE 1104 128 1024 128
WIRE 96 144 96 128
WIRE 272 144 272 128
WIRE 368 144 368 128
WIRE 560 144 560 128
WIRE 768 144 768 128
WIRE 928 144 928 128
WIRE 1024 144 1024 128
WIRE 96 256 96 224
WIRE 272 256 272 224
WIRE 272 256 96 256
WIRE 368 256 368 224
WIRE 368 256 272 256
WIRE 448 256 368 256
WIRE 496 256 448 256
WIRE 560 256 560 224
WIRE 560 256 496 256
WIRE 768 256 768 224
WIRE 768 256 560 256
WIRE 928 256 928 224
WIRE 928 256 768 256
WIRE 1024 256 1024 224
WIRE 1024 256 928 256
WIRE 1104 256 1024 256
WIRE 496 352 496 256
FLAG 32 128 VA
IOPIN 32 128 In
FLAG 400 64 VB
IOPIN 400 64 In
FLAG 1104 128 OUT
IOPIN 1104 128 Out
FLAG 416 128 OUTA
FLAG 448 256 Vlow
FLAG 496 352 0
SYMBOL bi 96 144 R0
SYMATTR InstName B2
SYMATTR Value I={gm}*V(VA)
SYMBOL res 256 128 R0
SYMATTR InstName RD2
SYMATTR Value {rd}
SYMBOL res 1008 128 R0
SYMATTR InstName RD7
SYMATTR Value {rd}
SYMBOL bi 768 144 R0
SYMATTR InstName B7
SYMATTR Value I={gm}*V(VB)
SYMBOL res 352 128 R0
SYMATTR InstName RM4
SYMATTR Value {1/gm}
SYMBOL bi 560 144 R0
SYMATTR InstName B5
SYMATTR Value I={gm}*V(OUTA)
SYMBOL res 912 128 R0
SYMATTR InstName RD5
SYMATTR Value {rd}
TEXT 544 0 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u \n+ VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u \n+VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 88 312 Left 2 !VREF VREF 0 3.33\nVB VB 0 SINE(0 0.005 10k) AC 1\nVDD VDD 0 10\nV1 VA 0 SINE(0 0.005 10k 0 0 180) AC 1
TEXT 792 344 Left 2 !.tran 0 0.5m 0
TEXT 792 304 Left 2 !;ac oct 10 1 1MEG
TEXT 528 312 Left 2 ;Differenzverstaerker
TEXT 32 104 Left 2 ;G2
TEXT 432 48 Right 2 ;G7
TEXT 88 280 Left 2 ;S
TEXT 608 272 Left 2 ;S
TEXT 80 8 Left 2 !.param gm=1m
TEXT 72 40 Left 2 !.param rd=100k

Bei der Differenzverstärkung ist Δ U_A = - Δ U_B und Δ I_A = - Δ I_B. Damit bleibt der Knoten V_low auf konstanten Potential und M6 kann im Kleinsignalersatzschaltbild wegfallen.
Gleichtaktverstärkung: u_A = u_B
v_gl ist hier wegen der Näherung

$r_{m4} \ll r_{D2}$ gleich 0.
Berücksichtigt man die Näherung, ergibt sich:

$u_{out} = - \left( 1 - \left( r_{D2} || r_{m4} \right) \cdot g_{m5} \right) u_{a} \cdot g_{m7} \cdot \left( r_{d5} || r_{d7} \right)$

$v_{gl} = - \left( 1 - \frac{r_{D2} || r_{m4}}{r_{m4}}\right) \cdot 2 \cdot v_{D}$
Bei den bisherigen Beispielen war r_D ≈ 100 · r_m.

$v_{gl} = \left( 1 - \frac{1}{1 + \frac{r_{m4}}{ r_{D2}}} \right) \cdot 2 \cdot v_{D} = 0.02 \cdot v_{D}$

Gleichtaktverstärkung: v_Gl mit M6

UDSM6 ändert sich:

M6 Ausgangswiderstand

Man betrachtet aus Symmetriegründen nur die Hälfte der Schaltung: M6, M7, M5
Sourceschaltung mit Stromquellen als Last und Gegenkopplung

Parallelwiderstand

$v_{Gl} = \frac{v_{out}}{v_{B}} = \frac{I \cdot r_{D5}}{v_{GS7} - I \cdot 2 \cdot r_{D6}} = = \frac{1}{\frac{v_{GS7}}{I \cdot r_{D5}} - 2 \frac{r_{D6}}{r_{D5}}}$

$I = - g_m \cdot v_{GS7} \frac{r_{D7}||\left( r_{D5} + 2 \cdot r_{D6}\right)}{r_{D5} + 2 \cdot r_{D6}}$

$v_{Gl} = - \frac{1}{\frac{r_{D5} + 2 \cdot r_{D6}}{g_m \cdot \left( r_{D5} r_{D7}||\left( r_{D5} + 2 \cdot r_{D6}\right) \right)} + 2 \frac{r_{D6}}{r_{D5}}}$

$v_{Gl} = - \frac{1}{\frac{r_{D5} + 2 \cdot r_{D6} + r_{D7}}{g_m \cdot r_{D5} \cdot r_{D7} } + 2 \frac{r_{D6}}{r_{D5}}}$

$v_{Gl} = - \frac{r_{D5}}{2 \cdot r_{D6}} \frac{1}{1 + \frac{r_{D5} + 2 \cdot r_{D6} + r_{D7}}{2 \cdot g_m \cdot r_{D6} \cdot r_{D7} }} \approx - \frac{r_{D5}}{2 \cdot r_{D6}}$

$v_{Gl} = - \frac{r_{D5}}{2 \cdot r_{D6}}$

Mit M6 kann man die Gleichtaktverstärkung klein halten.
Störsignale auf beiden Eingängen A und B erscheinen nicht am Ausgang und werden unterdrückt.

MOSDiff3.asc

Version 4
SHEET 1 1356 680
WIRE 512 -32 416 -32
WIRE 592 -32 512 -32
WIRE 656 -32 592 -32
WIRE 416 -16 416 -32
WIRE 416 -16 368 -16
WIRE 592 -16 592 -32
WIRE 368 32 368 -16
WIRE 416 32 368 32
WIRE 656 32 656 -32
WIRE 656 32 592 32
WIRE 496 64 464 64
WIRE 544 64 496 64
WIRE 416 96 416 80
WIRE 416 96 352 96
WIRE 496 96 496 64
WIRE 496 96 416 96
WIRE 592 96 592 80
WIRE 688 96 592 96
WIRE 416 112 416 96
WIRE 592 112 592 96
WIRE 432 160 416 160
WIRE 592 160 576 160
WIRE 368 192 352 192
WIRE 688 192 640 192
WIRE 432 208 432 160
WIRE 432 208 416 208
WIRE 576 208 576 160
WIRE 592 208 576 208
WIRE 416 256 416 208
WIRE 480 256 416 256
WIRE 512 256 480 256
WIRE 592 256 592 208
WIRE 592 256 512 256
WIRE 496 304 480 304
WIRE 432 336 304 336
WIRE 480 384 480 352
WIRE 496 384 496 304
WIRE 496 384 480 384
WIRE 480 400 480 384
FLAG 480 400 0
FLAG 512 -32 VDD
IOPIN 512 -32 In
FLAG 352 192 VA
IOPIN 352 192 In
FLAG 688 192 VB
IOPIN 688 192 In
FLAG 688 96 OUT
IOPIN 688 96 Out
FLAG 352 96 OUTA
IOPIN 352 96 Out
FLAG 512 256 Vlow
FLAG 304 336 Vref
SYMBOL nmos4 368 112 R0
WINDOW 3 83 72 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M2
SYMBOL pmos4 464 -16 M0
SYMATTR InstName M4
SYMATTR Value CD4007P
SYMBOL pmos4 544 -16 R0
WINDOW 3 56 73 Left 2
SYMATTR Value CD4007P
SYMATTR InstName M5
SYMBOL nmos4 432 256 R0
WINDOW 3 77 58 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M6
SYMBOL nmos4 640 112 M0
WINDOW 3 -77 121 Left 2
SYMATTR Value CD4007N
SYMATTR InstName M7
TEXT 272 -152 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=1.48 LAMBDA=0.018 CGDO=400n)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-1.48 LAMBDA=0.018 CGDO=400n)
TEXT 312 456 Left 2 !VREF VREF 0 3.33\nVB VB 0 5\nVDD VDD 0 10\nV1 VA 0 SINE(5 0.005 10k) AC 1
TEXT 688 480 Left 2 !.tran 0 0.5m 0
TEXT 688 448 Left 2 !;ac oct 10 1 1MEG
TEXT 536 384 Left 2 ;Differenzverstaerker

Gleichtaktunterdrückung

Common mode rejection rate (CMRR)
Angabe in Dezibel (dB)
$G = \frac{v_{D}}{v_{Gl}} = \frac{g_m \left( r_{D2} || r_{D4}\right)} {\frac{r_{D4}}{2 \cdot r_{D6}}} = \frac{2 \cdot g_m \cdot r_{D2} \cdot r_{D6}}{r_{D2}+r_{D4}}$
$CMRR = 20 log G$
Power supply rejection ratio (PSRR)

Änderung des Ausgangssignals bei Spannungsversorgungsänderung

CMOS Operationsverstärker TLC272 gebondeter Chip

Man kann integrierte Bauelemente auch als Wafer oder Chips bekommen.
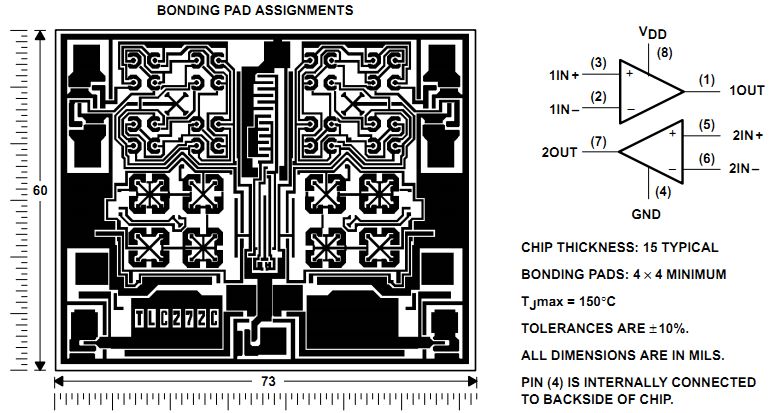
Das Bild zeigt den Chip TLC272 dessen Bondpads mit feinen Golddrähten (25 µm Dicke) mit dem Gehäuse verbunden sind.
Pin 1 ist bei dem Bild rechts oben, damit die Eingänge links und die Ausgänge rechts sind.
Die Chips wurden hier an der Hochschule Kempten im Labor Mikrosystemtechnik gebondet.
Es befinden sich 2 Operationsverstäker auf dem Chip. Einer oben und einer unten.
Die Spannungsversorgungspads befinden sich in der Mitte rechts (VDD) und links (GND).
Links oben und unten befinden sich jeweils die beiden Eingänge.
Links In+ rechts In-.
Rechts oben und unten befinden sich die Ausgänge.
Der Chip ist 1.524 mm x 1.8542 mm (60 mil x 73 mil) gross.
Weitere Informationen findet man auch im Datenblatt.

CMOS Operationsverstärker TLC272

Quelle: Texas Instruments Datenblatt tlc272a.pdf

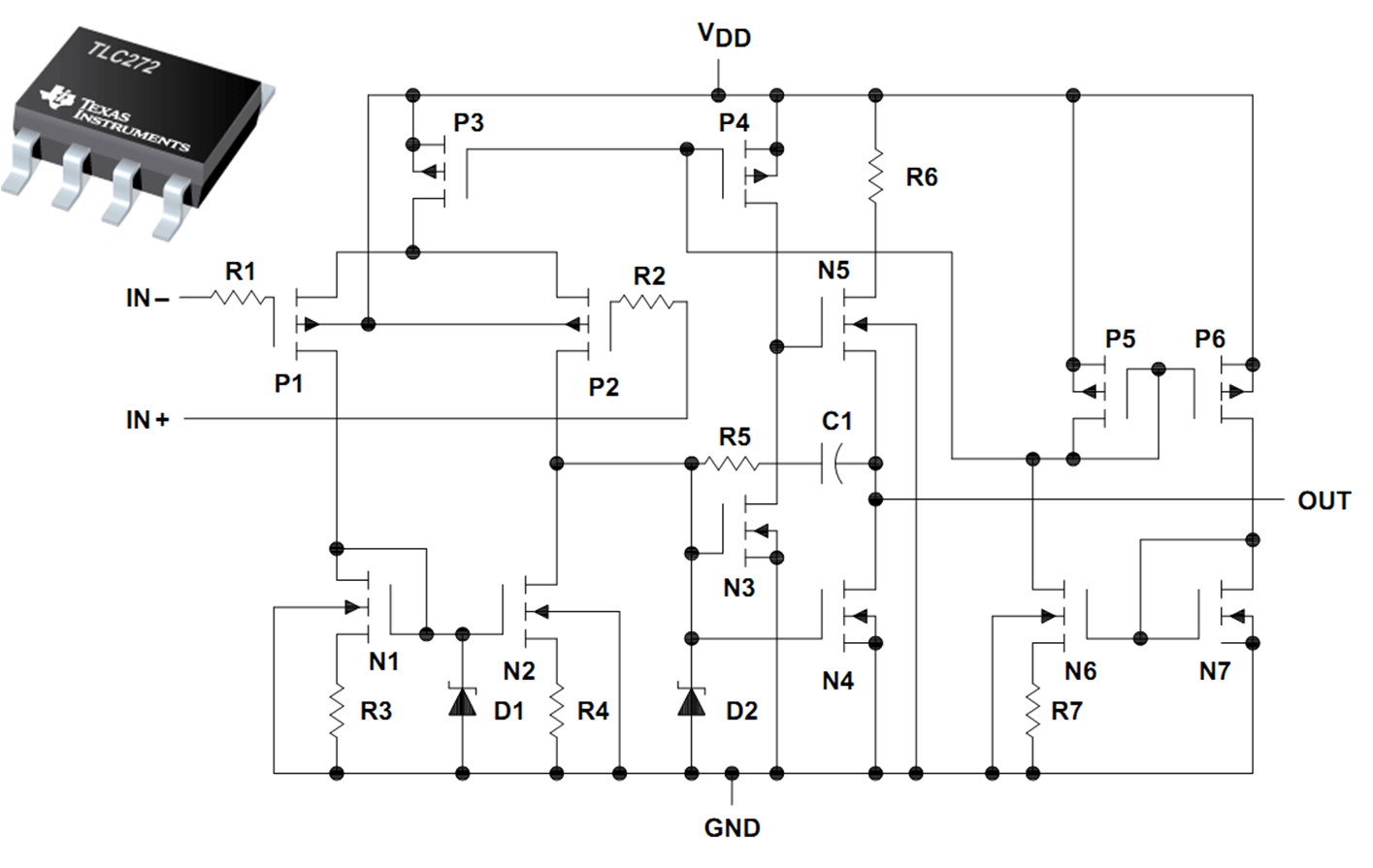
Referenzstromquelle rechts: P5, P6, N6, N7, R7
Differenzverstärker: P1, P2, P3, N1, N2
Zenerdiode für den Startup
2.te Verstärkerstufe: Sourceschaltung: N3, P4
Ausgangsstufe: N4, N5
Frequenzgangkompensation: R5, C1

Input/Output rail-to-rail Operationsverstärker:
TLV246
MCP6022

Nächstes Mal:

MOSFET-Stromquelle
Differenzverstärkerschaltung und Messung
Input/Output rail-to-rail Operationsverstärker MCP6022

07 Bipolartransistor

2023 Elektronik 3 06 MOSFET Prof. Dr. Joerg Vollrath

Elektronik 3

06 MOSFET

Prof. Dr. Jörg Vollrath

Rückblick und Heute

NFET Kennlinienfeld

Wie sieht der Querschnitt und das Kennlinienfeld eines PFETS aus?

Die Gleichung des n-Kanal MOSFETs

Stromspiegel

Man kann mit einem Stromspiegel durch die Wahl eines geeigneten Weitenverhältnisses oder der Anzahl der Transistoren einen Strom verstärken.

Ausgangswiderstand des Stromspiegels

Beispiel MOS Stromspiegel

Nachdenken über die Lösung

Simulation und Demonstration

Differenzverstärker: Schaltbild

Gegentakt, Differenzverstärker, Signale

Funktionsweise des Differenzverstärkers

Differenzverstärker Simulation und Demonstration

Gegentakt- oder Differenzverstärkung vD KESB

Gleichtaktverstärkung: vGl mit M6

Gleichtaktunterdrückung

CMOS Operationsverstärker TLC272 gebondeter Chip

CMOS Operationsverstärker TLC272

Nächstes Mal:

Gegentakt- oder Differenzverstärkung v_D KESB

Gleichtaktverstärkung: v_Gl mit M6