Elektronik 3

08 Rauschen

Prof. Dr. Jörg Vollrath

07 Bipolartransistor

Video Rauschen

Rückblick und Heute

Bipolartransistor
Gleichung, Modell, physikalischer Aufbau
BJT Verstärker

Heute: Rauschen

Definition
Widerstandsrauschen
Diodenrauschen
Transistorrauschen
Rauschspannung
Rauschfaktor
SPICE Simulation

Reinhold: Kap. 7; S. 125-131
Jaeger: p. 1204,p. 823

Motivation Rauschen

Warum interessiert mich Rauschen?

Damit wird das kleinste zu detektierende Signal begrenzt:
Diode als Temperaturmesser: 0.2 mV/K
Wägezelle, Dehnungsmesstreifen:
Handysignal:
Messgenauigkeit Oszilloskop
Wie geht man mit Rauschen um?
Bandbreite, Mittelwertbildung, Verstärkung
R, andere Rauschquellen und C

Sie können Rauschquellen in eine Schaltung einzeichnen und den Beitrag am Ausgang der Schaltung berechnen.

Rauschen

Ein störendes Signal in einem Schaltkreis
Versuchsaufbau

Quelle, Schaltung, Messgerät (Oszilloskop, Spektrum Analysator)

Oszilloskop Messung

Zeit: x-Achse
Amplitude: y-Achse
Überlagerung von verschiedenen Frequenzen

Spektrum Analysator

Frequenz: x-Achse
Leistung (Amplitude):
y-Achse
Angabe: Rauschspannung $\frac{V}{\sqrt{Hz}}$

Rauschen und das Oszilloskop

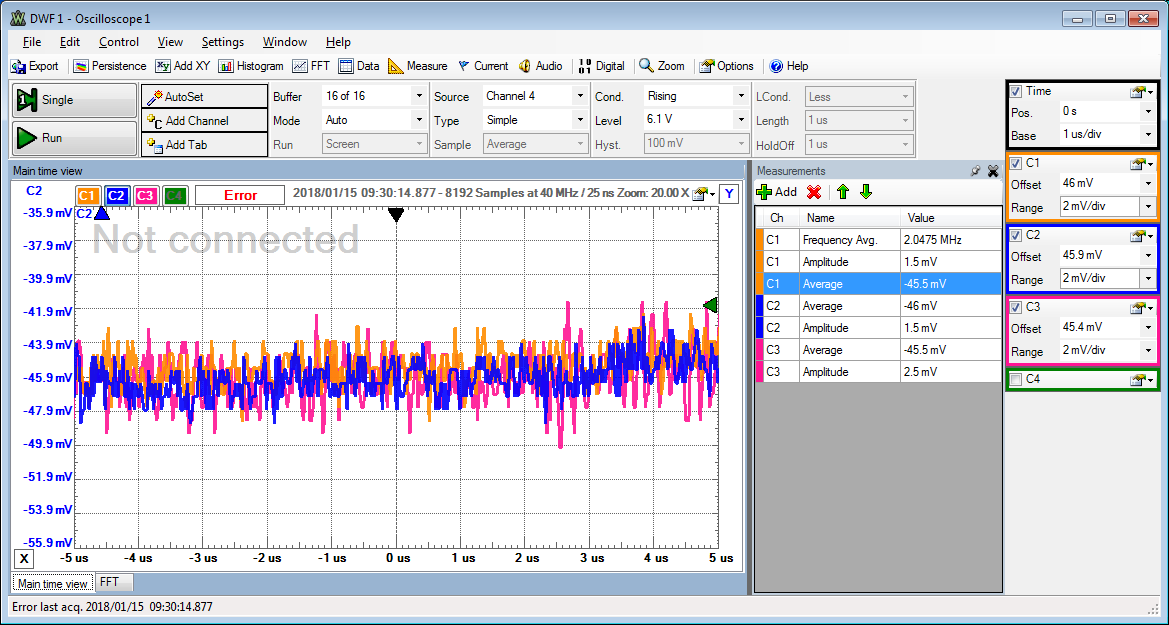
Am Oszilloskopbild kann man das Rauschen durch zufällige Werte um einen Mittelwert herum sehen.
Es gibt einen Mittelwert und einen Effektivwert (RMS: root mean square).

$U_{RMS} = \sqrt{U_{DC}^2 + U_{noise}^2}$

Bei dieser Darstellung treten nur diskrete Spannungswerte mit einer Schrittweite von ca. 1 mV auf. Diese Auflösung wird von der Auflösung des Analog-Digitalwandlers vorgegeben.

Man kann das Signal mit einer FFT in den Frequenzbereich übertragen.

Eingangsbezogenes Rauschen

Messung am Ausgang
Wie überlagert sich das Rauschen dem Quellsignal?

Verstärkung A

Beispiel

An einem Verstärker mit einer Verstärkung von 100 wird ein weißes Rauschspektrum (konstant über der Frequenz) von Gleichspannung bis 100MHz von

$10 \frac{nV}{\sqrt{Hz}}$ gemessen.
Berechnen Sie die Eingangsrauschspannung.

$U_{onoise}^{2}(f)=(10 \frac{nV}{\sqrt{Hz}})^2 = 100 \cdot 10^{-18} \frac{V^2}{Hz}$
Berechnung des Effektivwertes am Ausgang mit Hilfe der Bandbreite:

$U_{onoise,rms} = \sqrt{\int_{0}^{100MHz} 100 \cdot 10^{-18} df } V = 100 \mu V$
Transfer mit der Verstärkung zum Eingang:

$U_{inoise,rms} = \frac{U_{onoise,rms}}{A} = 1 \mu V$
Wie groß ist die Spitze-Spitze-Spannung (peak-to-peak)?
Multipliziere den Effektivwert mit 6.6

$U_{onoisepp} = 6.6 \cdot 100 \mu V = 660 \mu V$

Widerstandsrauschen

Statistische Stromschwankung durch thermische Bewegung der Ladungsträger.

Rauschstrom
Rauschspannung

Ersatzspannungsquelle
Ersatzstromquelle

Addition von Quellen:

$U_{r} = \sqrt{ \sum_{i=1}^{n} U_{ri}^{2}}$

$U_{rR}^2 (f) = 4 k T R$

$U_{rR,rms}^2 = \int U_{rR}^2 (f) df = 4 k T R \Delta f$

$U_{rR,rms} = \sqrt{4 k T R \Delta f}$

$I_{rR,rms} = \sqrt{\frac{4 k T \Delta f}{R}}$

Da Rauschspannungquellen nicht korreliert sind, keine feste Frequenz und Phasenbeziehung haben, wird die Gesamtspannung aus der Summe der Quadrate gebildet.
Die Leistungen addieren sich.

Beispiel: Δ f = 100 MHz
k = 13.8 · 10 ^-24 J/K
T = 300 K

R [Ω]	1k	100k	1M
U_r(f) [nV Hz^-0.5]	4.1	41	129
U_rms [mV]	0.04	0.4	1.2
U_pp [mV]	0.24	2.44	7.7

Amplitude, Spektrum, Histogram

Gaussverteilung

V_pp = 6.6 V_rms

(Cresting factor, Scheitelfaktor)

Simulation Rauschen mit FFT in Javascript

Kann man die Eigenschaften von weissen Rauschen mit einer Simulation bestätigen?

JavaScript

1. Versuch
Zufallszahlen erzeugt mit Math.random() 0..1
Erzeugung der FFT und des Histogramms
2. Versuch
Erzeugung der FFT mit zufälliger Phase
Erzeugung der Zeitdaten und des Histogramms.
Gaussverteilung, Vpp = 6.6 Vrms (Cresting factor, Scheitelfaktor)

Spektrum und Noise Density
Ein Spektrum verteilt den Effektivwert auf N_FFT einzelne Frequnezen.
Ein Spektrum normiert die Spectral Density mit 1 Hz.
A_e = 20 log(e_n)
Effektivwert vom Spektrum:
A_e + 20 * log(N_FFT/2)

Widerstandsrauschen

$U_{nR} = \sqrt{4 k T R BW}$

$U_{nR} = 0.128 \frac{nV}{\sqrt{\Omega Hz}}\sqrt{R BW}$

$BW = \frac{\pi}{2} f_{3dB}$

Es wird die Bandbreite BW eines Tiefpasses

$\frac{\pi}{2}$ zu Grunde gelegt.

Ein Widerstand von 1 MOhm hat bei einer Bandbreite von 100 Hz eine Rauschspannung größer 1 uV.
Thermisches Rauschen und Nyquist-Formel (Lokal)

R / Ω	BW / Hz	U_nR / V
10 k	10 k	1.28 µ
1 M	10 k	12.8 µ

Beispiel ohmsche Widerstände

Berechnen Sie die effektive eingangs- und ausgangsbezogene Rauschspannung im Bereich bis 1kHz.

Ersatzschaltbild ausgangsbezogene Rauschspannung Parallelschaltung: Stromquellen

$I_{10k}^{2}(f) = \frac{4kT}{R_1} = \frac{4 \cdot 13.8 \cdot 10^{-24} \cdot 300 }{10000} \frac{A^2}{Hz} = 1.66 \cdot 10^{-24} \frac{A^2}{Hz}$

$I_{1k}^{2}(f) = 16.6 \cdot 10^{-24} \frac{A^2}{Hz}$

$I_{10k,rms}^{2} = \int_{0}^{1kHz} I_{10k}^{2}(f) df = 1.66 \cdot 10^{-21} A^2$

$I_{1k,rms}^{2} = 16.6 \cdot 10^{-21} A^2$

$U_{rout,rms} = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{10k,rms}^{2} + I_{1k,rms}^{2}} = 123 nV$

$U_{rin,rms} = 123 nV \frac{R_1 + R_2}{R_2} = 1.35 \mu V$
Alternative Superposition:

$U_{10k}(f) = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{10k}^{2}(f)} = 1.2 \frac{nV}{\sqrt{Hz}}$

$U_{1k}(f) = \frac{R_1 \cdot R_2}{R_1 + R_2} \sqrt{I_{1k}^{2}(f)} = 3.7 \frac{nV}{\sqrt{Hz}}$

NoiseR.asc

Version 4
SHEET 1 880 680
WIRE 80 80 -32 80
WIRE 208 80 160 80
WIRE -32 96 -32 80
WIRE 208 128 208 80
WIRE -32 240 -32 176
WIRE 80 240 -32 240
WIRE 208 240 208 208
WIRE 208 240 80 240
WIRE 80 256 80 240
FLAG 80 256 0
FLAG 208 80 VA
SYMBOL voltage -32 80 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName VIN
SYMATTR Value ""
SYMBOL res 192 112 R0
SYMATTR InstName R2
SYMATTR Value 1k
SYMBOL res 176 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10k
TEXT -64 296 Left 2 !.noise v(VA,0) Vin dec 100 1 100000k
TEXT -56 32 Left 2 !.temp 300

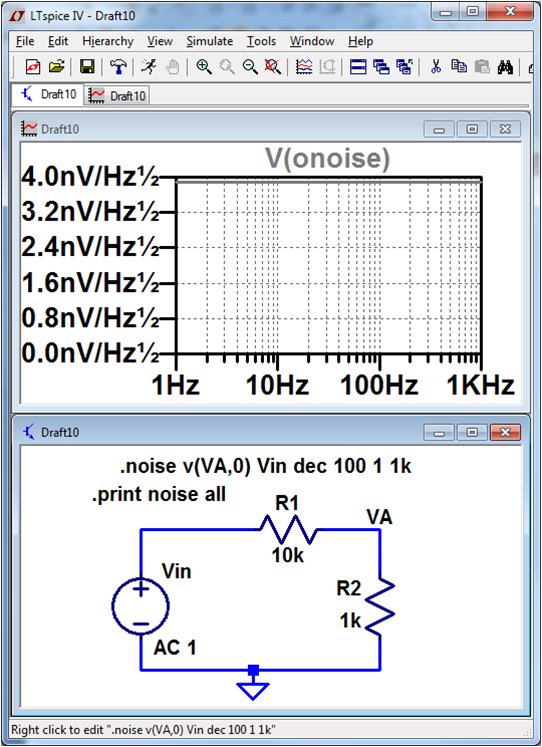
LTSPICE Verifikation

$U_{rout}(f) = 3.81 \frac{nV}{\sqrt{Hz}}$
'Strg' click auf die Beschriftung

$U_{rout, rms} = 122.7 nV$

Nachdenken über die Lösung

Je größer der Widerstand, desto größer die Rauschspannung
Einheiten
Quellenersatzschaltbild
Addition von Rauschspannungen und Strömen

Wurzel der Summe der Quadrate

Effektivwerte

Spannungsteiler um ein Signal auf den Eingangsbereich eines Verstärkers oder AD Wandlers an zu passen.

Beispiel RC Rauschen

Berechnen Sie die effektive ausgangsbezogene Rauschspannung.

$U_{out,noise}(f) = \sqrt{4 k T R } \frac{1}{1 + j \omega R C}$

$U_{out,noise,rms} = \sqrt{ \int_{0}^{f_{3db} \frac{\pi}{2}} U_{out,noise}^2 (f) df}$

$U_{out,noise,rms} = \sqrt{ f_{3db} \frac{\pi}{2} 4kTR}$

$U_{out,noise,rms} = \sqrt{ \frac{1}{2 \pi R C} \frac{\pi}{2} 4kTR} = \sqrt{ \frac{kT}{C} } = 64 \mu V$

NoiseRC.asc

Version 4
SHEET 1 880 680
WIRE 448 80 336 80
WIRE 576 80 528 80
WIRE 336 96 336 80
WIRE 576 144 576 80
WIRE 336 240 336 176
WIRE 448 240 336 240
WIRE 576 240 576 208
WIRE 576 240 448 240
WIRE 448 256 448 240
FLAG 448 256 0
FLAG 576 80 VA1
SYMBOL voltage 336 80 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName VIN
SYMATTR Value ""
SYMBOL res 544 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R4
SYMATTR Value 10k
SYMBOL cap 560 144 R0
SYMATTR InstName C1
SYMATTR Value 1pF
TEXT 272 296 Left 2 !.noise v(VA1,0) Vin dec 100 1 1000MEG
TEXT 360 328 Left 2 !.print noise all

Vergleich einer Mittelwertbildung und eines RC Schaltkreises.

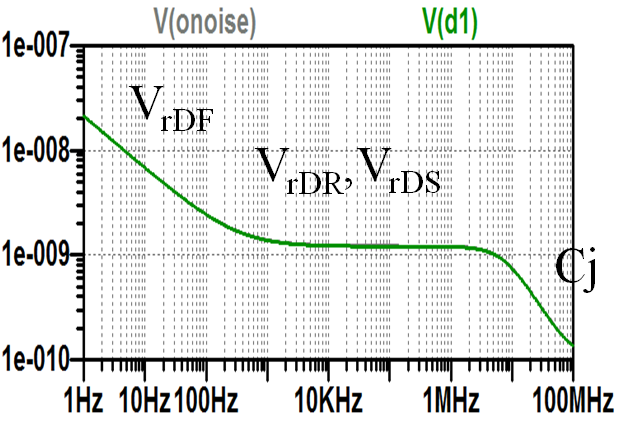
Diodenrauschen

Schrotrauschen (Shot noise)

Ladungsträger überschreiten Grenzflächen (Potenzialbarrieren)
$I_{rDS}(f)=\sqrt{2 q I}$
I Diodenstrom, Arbeitspunktstrom, q Elementarladung

Funkelrauschen (Flicker noise,1/f)
$I_{rDF}(f) = \sqrt{\frac{K_F I^{AF}}{f^{b}}}$

KF, AF und b Materialparameter
Silizium KF=10-16, AF=1, b=1

Thermisches Rauschen $I_{rDR}(f)$

Bahnwiderstände der Diode

Summe
$I_{rD}(f) = \sqrt{2 q I + \frac{K_F I^{AF}}{f^{b}} + I_{rDR}^{2} (f) }$

DiodeR.asc

Version 4
SHEET 1 1492 680
WIRE 96 96 -32 96
WIRE 240 96 176 96
WIRE -32 144 -32 96
WIRE 240 144 240 96
WIRE -32 256 -32 224
WIRE 96 256 -32 256
WIRE 240 256 240 208
WIRE 240 256 96 256
WIRE 96 272 96 256
FLAG 96 272 0
FLAG 240 96 VA
SYMBOL voltage -32 128 R0
WINDOW 3 15 131 Left 0
WINDOW 123 15 103 Left 0
WINDOW 39 0 0 Left 0
SYMATTR InstName Vin
SYMATTR Value 5
SYMATTR Value2 AC 1
SYMBOL res 192 80 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL diode 224 144 R0
SYMATTR InstName D1
SYMATTR Value 1N914x
TEXT -96 -40 Left 0 !.noise v(VA,0) Vin dec 100 1 100MEG
TEXT -96 -8 Left 0 !.model 1N914x D(Is=2.52n Rs=.568 N=1.752 Cjo=4p \n+ KF=1E-16 AF=1 M=.4 tt=20n Iave=200m Vpk=75 \n+ mfg=Motorola type=silicon)

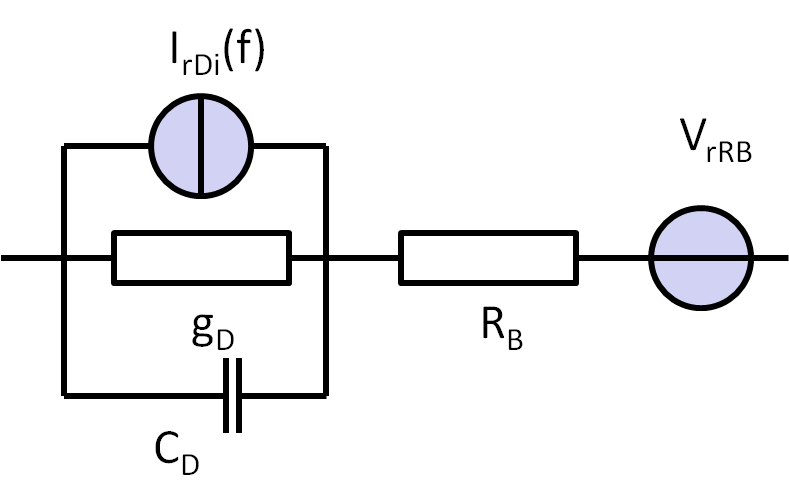
Diodenrauschersatzschaltung

Zwei Quellen:

Strom
$I_{rDi} = \sqrt{2 1 I \Delta f + \frac{K_F I^{AF} \Delta f}{}f^{b}}$
Spannungsquelle für den Bahnwiderstand
$V_{rRB} = \sqrt{4kTR \Delta f}$

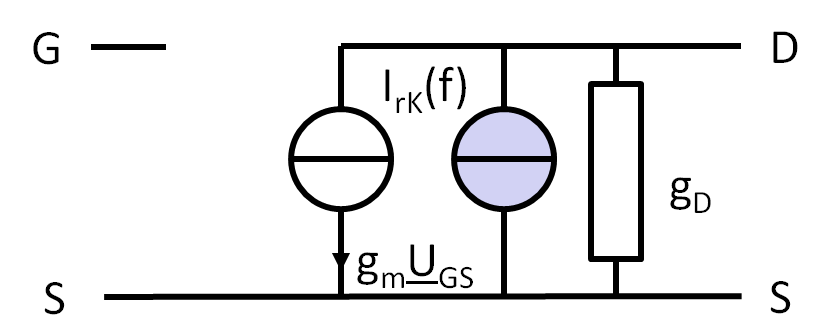
Transistorrauschen

Bipolartransistor: Diode BE, BC
Feldeffekttransistor
- Kanalrauschen I_rK
- 1/f Rauschen IrKF
- Thermisches Kanalrauschen IrKt
- Schrotrauschen Drain-Bulk, Source Bulk

$I_{rK}(f) = \sqrt{I_{rKt}^{2}(f) + I_{rKF}^{2}(f)}$

$I_{rKF}(f) = \sqrt{\frac{K_F I_D^{AF}}{C_{ox} f^b}}$

$I_{rKt}(f) = \sqrt{\frac{8}{3} k T g_m }$

Rauschfaktor

Signal Rausch Abstand

Signal to noise ratio (SNR)
Quotient aus Signalleistung P_s und Rauschleistung P_r

Rauschfaktor, Rauschzahl:
- Verhältnis der Signalrauschabstände von Eingang und Ausgang
Rauschmaß: logarithmierter Rauschfaktor

$SNR = \frac{P_S}{P_r}$

$SNR_{dB} = 10 \cdot log \left( \frac{P_S}{P_r} \right) = 10 \cdot log \left(P_S\right) - 10 \cdot log \left(P_r\right)$

$F = \frac{SNR_E}{SNR_A}$

$F_{dB} = 10 \cdot log \left( F \right)$

Rauschen eines Operationsverstärkers

Das Rauschen eines Operationsverstärkers kann durch eine weisse Rauschstromquelle i_eop und eine weisse Rauschspannungsquelle v_eop modelliert werden.
Die Beschaltung mit Widerständen enthält zusätzliche Rauschquellen.
Für jede Quelle wird die Ausgangsrauschspannung für eine gegebene Bandbreite mit der Übertragungsfunktion bestimmt
Die Spannungsquellen werden zusammengefasst.
Wurzel der Summe der Quadrate

NoiseOpAmp.asc

Version 4
SHEET 1 880 680
WIRE 48 128 32 128
WIRE 272 128 48 128
WIRE 48 144 48 128
WIRE 352 144 336 144
WIRE 272 160 256 160
WIRE 160 192 128 192
WIRE 256 192 256 160
WIRE 256 192 240 192
WIRE 48 256 48 224
FLAG 48 256 0
FLAG 352 144 Vout
FLAG 128 192 Inp
FLAG 32 128 Inm
SYMBOL voltage 256 192 R90
WINDOW 0 -32 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Veop
SYMATTR Value 3.76�
SYMBOL current 48 144 R0
SYMATTR InstName Ieop
SYMATTR Value 37.6p
SYMBOL Opamps\\opamp 304 80 R0
SYMATTR InstName U1
TEXT 416 176 Left 2 !.op
TEXT 72 264 Left 2 !.include opamp.sub

Berechnung Rauschen einer Opamp Schaltung

Berechnen Sie den Effektivwert der äquivalenten Rauschspannung am Ausgang.

T = 27 C = 300 K
R1 = 4kΩ
R2 = 1kΩ
v_eop = 3 nV/

$\sqrt{Hz}$
i_eop = 30 fA/

$\sqrt{Hz}$
GBW = 10 MHz
Berechnen Sie den Beitrag der einzelnen Rauschquellen am Ausgang.
Wie groß ist die äquivalente Ausgangsspannungsquelle?
Welchen peak to peak Wert der Ausgangsrauschspannung erwarten Sie?
Wie groß ist die äquivalente Eingangsrauschspannungsquelle?

OpNonInvRausch.asc

Version 4
SHEET 1 880 680
WIRE 96 -192 32 -192
WIRE 192 -176 160 -176
WIRE 272 -176 192 -176
WIRE 96 -160 80 -160
WIRE 192 -160 192 -176
WIRE 80 -80 80 -160
WIRE 128 -80 80 -80
WIRE 192 -80 128 -80
WIRE 192 -64 192 -80
FLAG 192 16 0
FLAG 32 -192 Ve
IOPIN 32 -192 In
FLAG 272 -176 Va
IOPIN 272 -176 Out
FLAG 128 -80 Vx
SYMBOL Opamps\\opamp 128 -112 M180
SYMATTR InstName U2
SYMBOL res 176 -176 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 4k
SYMATTR InstName R1
SYMBOL res 176 -80 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 1k
SYMATTR InstName R2
TEXT -24 -240 Left 2 !.include opamp.sub
TEXT -24 -272 Left 2 !VE VE 0 DC 0
TEXT -24 -312 Left 2 !;dc Ve -1 1 0.05
TEXT -24 56 Left 2 !.noise V(va) Ve dec 10 1 100k

Berechnung Rauschen einer Opamp Schaltung

Berechnen Sie den Effektivwert der äquivalenten Rauschspannung am Ausgang.

T = 80 C
R1 = 4kΩ
R2 = 1kΩ
v_eop = 3 nV/

$\sqrt{Hz}$
i_eop = 30 fA/

OpNonInvRauschQ.asc

Version 4
SHEET 1 880 680
WIRE -48 -192 -64 -192
WIRE 96 -192 32 -192
WIRE 192 -176 160 -176
WIRE 272 -176 192 -176
WIRE 96 -160 80 -160
WIRE 192 -144 192 -176
WIRE 192 -48 192 -64
WIRE 80 32 80 -160
WIRE 192 32 80 32
WIRE 192 48 192 32
WIRE 80 64 80 32
WIRE 80 208 80 144
FLAG 192 208 0
FLAG -64 -192 Ve
IOPIN -64 -192 In
FLAG 272 -176 Va
IOPIN 272 -176 Out
FLAG 80 208 0
SYMBOL Opamps\\opamp 128 -112 M180
SYMATTR InstName U2
SYMBOL res 176 -64 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 4k
SYMATTR InstName R1
SYMBOL res 176 112 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 1k
SYMATTR InstName R2
SYMBOL voltage 48 -192 R90
WINDOW 0 -32 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName V3
SYMATTR Value 3.76�
SYMBOL voltage 192 32 R0
SYMATTR InstName V2
SYMBOL voltage 192 -160 R0
SYMATTR InstName V1
SYMBOL current 80 144 R180
WINDOW 0 24 80 Left 2
WINDOW 3 24 0 Left 2
SYMATTR InstName I1
SYMATTR Value 37.6p
TEXT 104 -232 Left 2 !.include opamp.sub
TEXT -112 -112 Left 2 !VE VE 0 DC 0
TEXT -120 -64 Left 2 !;dc Ve -1 1 0.05
TEXT 16 -264 Left 2 !.noise V(va) Ve dec 10 1 100k

Für die Berechnung des Effektivwertes der äquivalenten Rauschspannung benötigt man die Bandbreite.
GBW = 10 MHz
Verstärkung des Operationsverstärkers:

$v_u = \frac{v_a}{v_e} = \frac{R_1 + R_2}{R_2} = 5$
Grenzfrequenz des Operationsverstärkers:

$f_g = \frac{GBW}{v_u} = 2 MHz$
Bandbreite für die Rauschspannung (RC-Glied):

$f_{BW} = \frac{\pi}{2} f_g = 3.14 MHz$

Berechnung der Effektivwerte der Rauschspannungs- und Stromquellen:

$v_{eoprms} = v_{eop} \cdot \sqrt{f_{BW}} = 5.3 \mu V$

$i_{eoprms} = i_{eop} \cdot \sqrt{f_{BW}} = 53 pA$

$v_{R1rms} = \sqrt{4 k T R_1 f_{BW}} = 14.4 \mu V$

$v_{R2rms} = \sqrt{4 k T R_2 f_{BW}} = 7.2 \mu V$

Superposition der Rauschquellen

1) v_eop

$v_{a veop rms} = v_u * v_{eoprms} = 26.5 \mu V$

2) I_eop
Ein invertierender Operationsverstärker mit der Eingangsspannung

$v_i = i_{eop} * R_2$

$v_{a ieop rms} = v_i \cdot \frac{R_1}{R_2} = i_{eop} \cdot R_1 = 212 nV$

3) v_noiseR2
Ein invertierender Operationsverstärker mit der Eingangsspannung v_R2rms

$v_{a R2 rms} = v_{R2rms} \cdot \frac{R_1}{R_2} = 28.8 \mu V$

4) v_noiseR1

$v_{a R1 rms} = v_{R1rms} = 14.4 \mu V$

Gesamtspannung:

$v_{a rms} = \sqrt{ v_{a veop rms}^2 + v_{a ieop rms}^2 + v_{a R2 rms}^2 + v_{a R1 rms}^2} = 41.43 \mu V$

$v_{app} = 6.6 \cdot V_{a rms} = 273 \mu V$

Zusammenfassung Rauschen

Spannung oder Strom
Frequenzabhängige Größen: $V/\sqrt{Hz}, A/\sqrt{Hz}$
Mit einer FFT wird der Effektivwert auf N_FFT Frequenzen verteilt.
Amplitude 6.6-mal größer als Effektivwert
Effektivwert: $V_{r,RMS} = \sqrt{\int V_{rR}^2(f)df}$
Mehrere Quellen: Wurzel aus der Summe der Quadrate
Umrechnung der Quellen
Widerstand, Diode, Transistor

Thermisches Rauschen: 4kTR
R = 1 MΩ, f_bw = 100 MHz, U_rms = 1.2 mV, U_pp = 7.7 mV
Kapazitäten: RC Tiefpass
$U_{rms} = \sqrt{\frac{kT}{C}}$
C = 1 pF, U_rms = 64 µV
1/f Rauschen, Funkelrauschen: $\frac{K_F I^{AF}}{f^{b}}$
Schrotrauschen: 2qI

Kapazität: Tiefpass, begrenzt Rauschen
Signalrauschverhältnis
Rauschzahl

Sie können Rauschquellen in eine Schaltung einzeichnen und den Beitrag am Ausgang der Schaltung berechnen.

Nächstes Mal:

09 Hallmessung, Magnetfeldmessung, Solarzelle

2023 09 29 Elektronik 3 08 Rauschen Prof. Dr. Joerg Vollrath

Elektronik 3

08 Rauschen

Prof. Dr. Jörg Vollrath

Rückblick und Heute

Motivation Rauschen

Warum interessiert mich Rauschen?

Rauschen

Rauschen und das Oszilloskop

Eingangsbezogenes Rauschen

Beispiel

Widerstandsrauschen

Amplitude, Spektrum, Histogram

Gaussverteilung

Kann man die Eigenschaften von weissen Rauschen mit einer Simulation bestätigen?

Widerstandsrauschen

Beispiel ohmsche Widerstände

LTSPICE Verifikation

Nachdenken über die Lösung

Beispiel RC Rauschen

Diodenrauschen

Diodenrauschersatzschaltung

Transistorrauschen

Rauschfaktor

Rauschen eines Operationsverstärkers

Berechnung Rauschen einer Opamp Schaltung

Berechnung Rauschen einer Opamp Schaltung

Zusammenfassung Rauschen

Nächstes Mal: