Hochschule Kempten      
Fakultät Elektrotechnik      
Elektronik 3       Fachgebiet Elektronik, Prof. Vollrath      

Elektronik 3

11 Schaltregler

Prof. Dr. Jörg Vollrath


10 Längsregler


Video der 14. Vorlesung Schaltungstechnik 5.5.2021


Länge: 1:02:43
0:0:0 Schaltregler

0:1:37 5.17 Simple Buck Converter

0:3:18 Schaltfrequenz, Periodendauer, Duty Cycle

0:7:2 Schaltungsanalyse

0:8:22 Spulenstrom und Spannung

0:9:48 Signalverlauf

0:13:26 Ansatz Spannungsverhältnis

0:14:38 Spannungsverhältnis und Duty Cycle

0:16:18 LTSPICE Schaltbild (Falsche Diode)

0:18:28 Einschwingvorgang

0:20:18 Nur bei größerem Strom CCM

0:24:22 Wirkungsgrad (mit falscher Diode zu klein)

0:28:18 Ergebnis ohne Leistung an der Diode

0:31:18 Continous conduction mode CCM, Discontinous conduction mode

0:34:18 Mindeststrom Iamin für CCM

0:38:5 Ergebnis Iamin= T/2/L Ua (1 - Ua / Ue)

0:39:18 Dimensionierung L = T / 2 / Iamin Ua (1 - Ua / Ue)

0:44:8 Welligkeit dUa

0:49:18 Faktor 4 oder 8 mit Tietze Schenk

0:54:38 Faktor 8

0:56:18 Kapazitätsdimensionierung für dUa

0:58:23 Welligkeit 30 mV, T = 4 us, L = 18 uH, Ue =12 V, Ua = 6 V

1:0:48 Iamin Rechnung

1:1:58 C = 10 uF

1:4:48 LT3570 Beipielsimulation

1:8:18 Power on sequence

1:9:48 Zu niedrige Ausgangsspannung wegen R8, Ri = 1 Ohm an der Eingangsspannung

Übersicht

Schaltregler



Unit 6, 1-7

Analog Devices, Linear Technology: LT3570

Buck converter, Abwärtswandler


Halbleiterschaltungstechnik, Tietze, Schenk, 18.6.1 Abwärtswandler


Schaltbild Buck converter


T: Periodendauer ( Cycle time)
tEin: Einschaltdauer
tAus: Ausschaltdauer
D: Duty Cycle

\( D = \frac{t_{Ein}}{t_{Ein} + t_{Aus}} \)
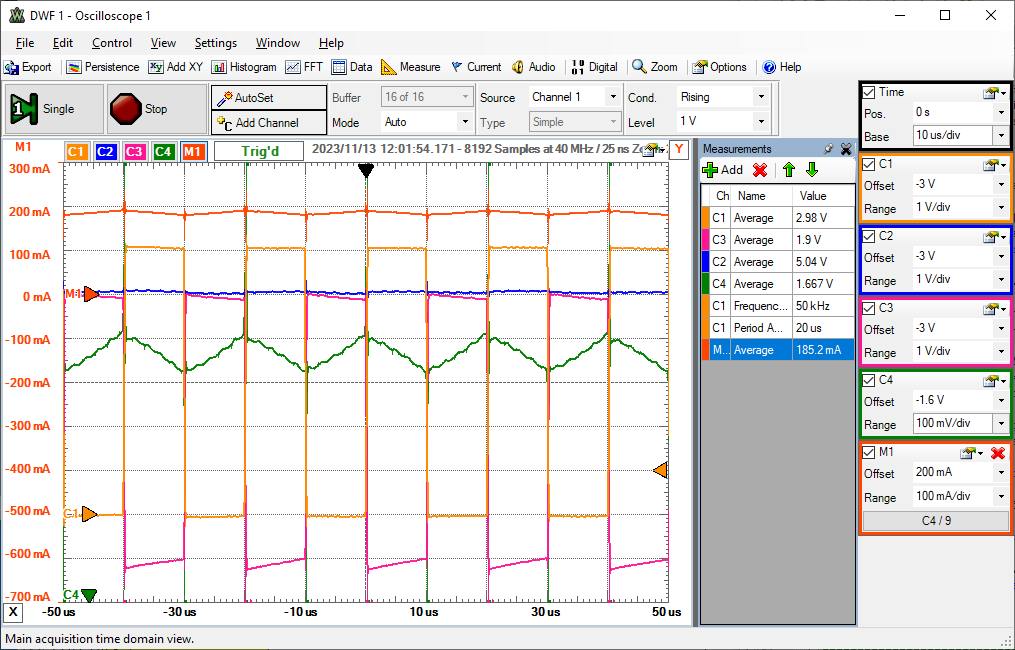
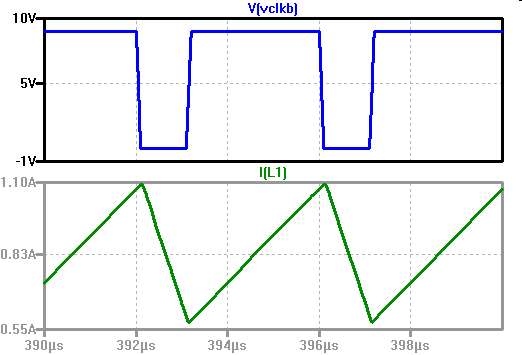Vclkb ist das invertierte VCLK1 signal.
Vclkb "high" der Transistor leitet, Schalter zu.

Continous Conduction Mode (CCM)

ILmin > 0

Ia,avg:Mittlerer Ausgangsstrom
d IL = ILmax - ILmin


Schaltbild

Eine externe Spannungsquelle wird mit einem Transistorschalter (Ein, verbunden) mit einer Reihenschaltung aus Spule und einer Kapazität verbunden.
Eine Diode schliesst den Schaltkreis, wenn der Transistor (Aus, offen) nichtleitend ist.

Je nach Stromverbrauch der Last und der Schaltungsauslegung kann man den Continous Conduction Mode (CCM, ILmin > 0 ), den Critical Conduction Mode ( ILmin gerade 0 ) und den Discontinous Conduction Mode (DCM, ILmin längere Zeit 0 ) unterscheiden.

Ausgangsspannung CCM


Spulenstrom und Spulenspannung:
\( U_L = L \cdot \frac{d I_L}{dt} \)
\( d I_L = \frac{1}{L} U_L dt \)

Einschaltzeit tEin:
UL = Ue - Ua

Ausschaltzeit tAus:
UL = - Ua

Stromänderung der Spule:
\( d I_L = \frac{1}{L} ( U_e - U_a ) t_{ein} = \frac{1}{L} U_a t_{aus} \)

\( ( U_e - U_a ) t_{ein} = U_a t_{aus} \)
\( U_e t_{ein} = U_a (t_{aus} + t_{ein} )\)

\( U_a = U_e \frac{ t_{ein}}{t_{aus} + t_{ein}} = U_e \frac{ t_{ein}}{T} = U_e D \)
Der Duty Cycle bestimmt die Ausgangsspannung.

Mindeststrom CCM

Stromänderung der Spule:
\( d I_L = \frac{1}{L} ( U_e - U_a ) t_{ein} \)

Für diese Betriebsart darf der Spulenstrom nie Null werden.
Der Ausgangsstrom muss größer sein als
\( I_{amin} = \frac{1}{2} d I_L \)


\( U_a = U_e \frac{ t_{ein}}{T} \)
\( t_{ein} = T \frac{U_a}{U_e} \)

\( I_{amin} = \frac{1}{2 L} ( U_e - U_a ) t_{ein} \)
\( I_{amin} = \frac{1}{2 L} ( U_e - U_a ) T \frac{U_a}{U_e} \)

\( I_{amin} = \frac{T}{2 L} U_a \left( 1 - \frac{U_a}{U_e} \right) \)

Ausgangsspannung DCM


Der Strom ist zeitweise Null.

Stromanstieg während der Einschaltzeit tEin von 0 auf:

\( I_L = \frac{1}{L} \cdot U_L \cdot t_{ein} \)

Der arithmetische Mittelwert während einer Periode ist dann:

\( I_{em} = \frac{1}{2} \cdot I_L \cdot \frac{t_{ein}}{T} \)

\( I_{em} = \frac{1}{2} \cdot \frac{1}{L} \cdot U_L \cdot t_{ein} \cdot \frac{t_{ein}}{T} \)

\( I_{em} = \frac{T}{2 L} \cdot U_L \cdot \frac{t_{ein}^2}{T^2} = \frac{T \cdot D^2}{2 L} \cdot \left( U_e - U_a \right) \)

Verlustfreie Schaltung: Leistungsbetrachtung

\( U_e I_{em} = U_a I_a \)

\( U_{a} = \frac{U_e^2 D^2 T}{ 2 L I_a + U_e D^2 T} \)

\( D = \sqrt{\frac{2 L}{T} \frac{U_a}{U_e ( U_e - U_a)} I_a} \)
Bei niedrigen Strömen muss für eine konstante Ausgangsspannung der Duty Cycle verringert werden.

Dimensionierung L


Man stellt die Gleichung für Iamin nach L um.

\( L = \frac{T}{2 I_{amin} } U_a \left( 1 - \frac{U_a}{U_e} \right) \)

Frequenz f, Schwingungsdauer T
T klein, L klein aber dynamische Schaltverluste, teurer Schalttransistor

Für kleine geometrische Dimensionen von Spannungsreglern sollte L klein sein.

Dimensionierung C Welligkeit


Kapazität:
\( d Ua = \frac{d Q}{C} \)
\( d Ua = \frac{ I dt}{C} \)
Der Strom des Kondensators während einer Periodendauer ist der Unterschied zum mittleren Strom.
Eine Flächenbetrachtung ergibt den Faktor 8.
Ein halbes (laden und entladen 1/2) Dreieck (1/2) mit der Höhe 1/2 dIL.

\( d Ua = \frac{ d I_L T}{ 8 C} \)

\( C = \frac{ T I_{amin}}{ 4 d Ua} \)

Mit der Welligkeit d Ua

Beispiel


Es soll ein Schaltregler entworfen werden der aus einer Eingangsspannung von 12 V eine Ausgangsspannung von 5 V mit einem Strom zwischen 0.1 und 1 A und einer Welligkeit von 200 mV erzeugt. Der Schaltregler wird mit 10 kHz im continous conduction mode (CCM) betrieben.
Bestimmen Sie den notwendigen Duty Cycle D, L und C.
Welchen Dutycycle benötigt man bei einem Stromverbrauch von 50 mA.

Schaltregler Simulation



In welchem Betriebsmodus ist man? DCM oder CCM?

\( I_{amin} = \frac{T}{2 L} U_a \left( 1 - \frac{U_a}{U_e} \right) \)
\( I_{amin} = \frac{4 \mu s}{2 \cdot 180 \mu H} 6 V \left( 1 - \frac{6 V}{12 V} \right) = 33 mA \)
Betriebsmodus CCM
\( D = \frac{U_a}{U_e} = 0.5 \)

\( d U_a = \frac{T I_{a min}}{4 C} = \frac{4 \mu s 33 mA}{4 \cdot 10 \mu F} = 3.3 mV \)
Simulation V(vout): 6.149 - 6.145 = 4 mV

Simulation Wirkungsgrad η
\( \eta = \frac{P_a}{P_e} = \frac{U_a \cdot I_a}{U_e \cdot I_e} = \frac{6.147 V \cdot 102.45 mA}{12 V \cdot 56.471 mA} = 92.9 \% \)

Da die Eingangsspannung doppelt so gross ist wie die Ausgangsspannung ist der Eingangsstrom etwa halb so gross wie der Ausgangsstrom.



In VP+ = 5 V (90 mA), Cin = 15 uF, IRF9530, C = 47 uF, Diode, RL = 9 Ω ( I = 1.65 V / RL = 180 mA), f = 50 kHz, L = 207 uH, LR = 4 Ω

Vout_Ripple = 80 mV
neff = Pout/Pin= (1.65 V * 180 mA) / (5 V * 90 mA) = 66%
Pin = 5 V * 90 mA = 450 mW
Pout = 1.65 V * 180 mA = 300 mW
PRL = 4 Ω * 180 mA * 180 mA = 130 mW
(PPFET = 1/4 * 100 mV * 90 mA = 22 mW)


Schaltregler



LT3570
Bei grossem R8 werden die Ausgangsspannungen nicht erreicht Buck, Boost, LDO
Evaluation Board DC1106A 170.- (2023)


Ladungspumpe, Pelliconi Charge pump,

  • MOS Transistor als Schalter: X1, X2, X3, X4
  • Ladungsspeicher C1, C2
  • Start: Alle Knoten 0 V.
  • Phase(1): Phi1 high (VDD), Phi2 low
    • M1:off, M9:on
    • M2:on, M8:off
    • In is charging C2: VDD
    • Out is connected to C1: VDD
  • Phase(2): Phi1 low, Phi2 high (VDD)
    • M1:on, M9:off
    • M2:off, M8:on
    • In is charging C1: VDD
    • Out is connected to C2: 2 VDD
  • C1,C2: 10 uF
  • C3: 1 uF
Eine Ladungspumpe kann Spannungen erzeugen, die größer sind als die Versorgungsspannung oder negativ sind. Jede Stufe erhöht oder erniedrigt die erzeugte Spannung um eine Versorgungsspannung.
Zum Verständnis der Schaltung führt man die Simulation per Hand durch.
Bei einer Änderung der Spannung an Phi1 wird die Spannungsdifferenz an C1 entsprechend verschoben.
Achtung: Bulk der PFETs muss mit der größten Spannung verbunden sein.

Bei negativen Spannungen wird Eingang und Ausgang vertauscht und der Bulk Anschluss der NFETs mit der negativsten Spannung verbunden.


Da im idealen Fall die Eingangsleistung gleich der Ausgangsleistung ist, wird bei erhöhter Spannung am Ausgang der Ausgangsstrom entsprechend kleiner.
Dies ist bei der Dimensionierung der Schaltung zu beachten.

Mehrere Stufen

  • Es dauert einige Zeit bis die Ausgangsspannung erreicht ist.
  • Ausgangsspannungsschwankungen
Bei n Stufen ergibt sich eine Spannung von n · VDD.

Praktische Realisierung

Ladungspumpe Spannungsverdopplung

Ladungspumpe          Ringoszillator

C = 470 nF, f = 1kHz, VDD = 4 V.
Bei der Ladungspumpe wird die Spannung ohne Last von 4 V auf 8 V verdoppelt.
Mit einer Last von 68kΩ reduziert sich die Spannung.

Takterzeugung: Ringoszillator




Vout [V] 2 3 4 5 6
f [kHz]2272100450068008900

Je höher die Spanung, desto größer die Frequenz.

Zusammenfassung und nächste Vorlesung



Nächstes Mal