Hochschule Kempten      
Fakultät Elektrotechnik      
Elektronik 3       Fachgebiet Elektronik, Prof. Vollrath      

Elektronik 3

20 Datenwandler Kennwerte

Prof. Dr. Jörg Vollrath


19 Datenwandler


Video der 20. Vorlesung 15.12.2021


Länge: 1:02:43
0:0:0 DAC Eigenschaften

0:1:18 Kennlinie und Tabelle DAC

0:3:3 Operationsverstärker für Anpassung Ausgangsbereich

0:4:50 Offset

0:6:54 Gain Error

0:8:45 LSB real

0:10:0 DAC Sinussignal

0:13:10 Formel zur Erzeugung eines Sinussignals

0:16:29 Sinus Lookup Table

0:18:22 Wie sehen Signale bei verschiedene Frequenzen aus

0:19:32 Aliasing, Perioden = 31 und = 1 sehen bei 32 Abtastpunkten gleich aus

0:21:50 Beispiel: LSB, Vout=2 V mit Vref=3.3V N=10 Bit

0:23:10 LSBabs

0:27:30 Genauigkeit LSB

0:30:20 Codeberechnung

0:38:30 Kalibrierung DAC

0:41:30 Konvertierung in Dualzahl

0:44:30 ADC Kenngrößen

0:45:58 ADC Kennlinie und Tabelle

0:50:0 Beispiel LSB

0:50:50 LSBabs und LSBrel

0:53:25 Kalibrierung ADC

0:55:52 Kennlinie, Offset, Gain Error

0:58:1 Beispiel Multimeter

0:59:35 Maximaler und minimaler Code

1:3:20 LTSPICE Model Skalierbarer 4-Bit DAC

1:6:5 LTSPICE Model Skalierbarer 4-Bit ADC

1:6:35 LTSPICE Test

Übersicht


Reinhold: Kap 17, 342-347

DAC Differential non linearity (DNL)


Schrittweite

Differential non linearity characterizes the step size (difference) between 2 successive codes.
Step size:     \( LSB = \frac{V(111) - V(000)}{2^{3}-1} = 1 V \)

The step size between 2 successive codes is normalized with LSB and calculated as DNL:

\( DNL(n) = \frac{ V(n) - V(n-1) - LSB}{LSB} \)


Since the LSB is calculated using the first and last code:
\( \sum DNL_i = 0 \)
The graph and the table represent the same data and contain the same information.

DAC Differential non linearity (DNL)


Schrittweite

Differential non linearity characterizes the step size (difference) between 2 successive codes.
Step size:     \( LSB = \frac{V(111) - V(000)}{2^{3}-1} = 1 V \)

The step size between 2 successive codes is normalized with LSB and calculated as DNL:

\( DNL(n) = \frac{ V(n) - V(n-1) - LSB}{LSB} \)


Since the LSB is calculated using the first and last code:
\( \sum DNL_i = 0 \)
The graph and the table represent the same data and contain the same information.

DAC Integral non linearity (INL)

Absolutwertabweichung


Integral non linearity characterizes the difference real and ideal transfer characteristics.
Step size:
\( LSB = \frac{V(111) - V(000)}{2^{3}-1} = 1 V \)

The difference between real and ideal curve is normalized with LSB and calculated as INL:

\( INL(n) = \frac{ V_{real}(n) - V_{ideal}(n)}{LSB} \)


Since the INL is calculated using the first and last code:
INL(000) = 0; INL(111) = 0;


The error of the output voltage should be less than ±1/2 LSB.
-1/2 LSB > INL > 1/2 LSB

DAC Integral non linearity (INL)

Absolutwertabweichung


Integral non linearity characterizes the difference real and ideal transfer characteristics.
Step size:
\( LSB = \frac{V(111) - V(000)}{2^{3}-1} = 1 V \)

The difference between real and ideal curve is normalized with LSB and calculated as INL:

\( INL(n) = \frac{ V_{real}(n) - V_{ideal}(n)}{LSB} \)


Since the INL is calculated using the first and last code:
INL(000) = 0; INL(111) = 0;


\( INL(n) = \sum_{i=0}^n{ DNL(i)} \)

The error of the output voltage should be less than ±1/2 LSB.
-1/2 LSB > INL > 1/2 LSB

How to measure INL and DNL?

DAC:
Apply digital code and use a good voltmeter to measure corresponding analog output.
Noise can be filtered with averaging.

ADC:
Transition voltages have to be measured.
Noisy transitions.
Provide slow ramp and measure transition voltage.

Die Auflösung des Messgerätes sollte mindestens 4 mal so gross sein, wie die Auflösung der zu messenden Schaltung.

Characterization System




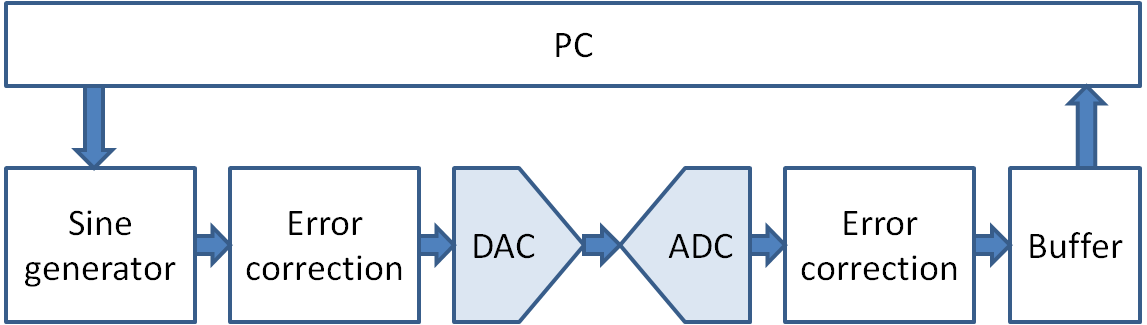
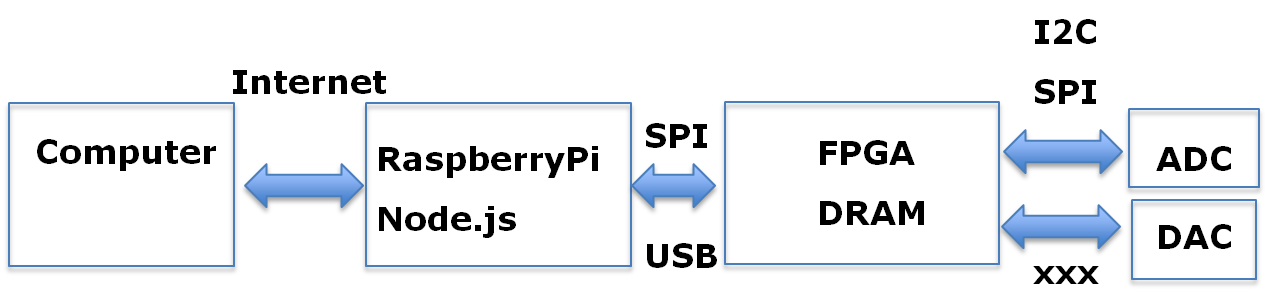
Characterization Waveforms

Rampe


Offset, Gain, INL, DNL
Rechteck
Settling time
<<Sinus
Signal to noise ratio

DAC Settling Time

  • Data Conversion Handbook p.292
  • Full scale settling time: 000...111
    • Linear Technolgy (AN120f)
    • Analog Devices MT-013
  • Mid scale settling time: 011..100
    • Analog Devices MT-013

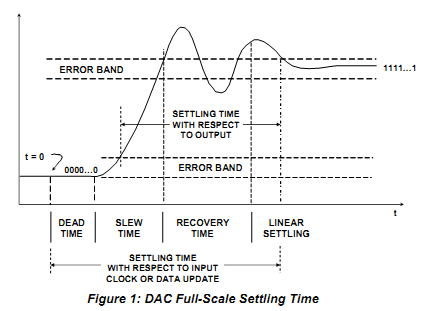
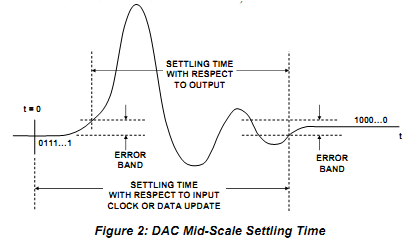
Quantization Error

Quantization error is the difference between the quantized signal and the original signal.

The quantization error stays between \( \pm \frac{1}{2} LSB \) for the input range.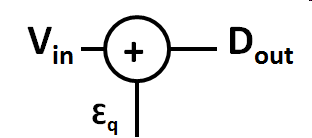
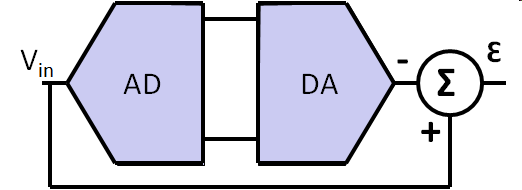
Quantization error can be modeled adding an extra signal εq to the original signal.

ADC dynamic range

First approximation:

Vsp: signal peak full scale voltage
Vqp: peak quantization noise voltage

\( SNR \approx 20 \cdot log\frac{V_{sp}}{V_{qp}} \)

\( SNR \approx 20 \cdot log\frac{LSB \cdot 2^{N}}{LSB} dB \)

\( SNR = 20 \cdot N \cdot log(2) \)

\( SNR = 6.02 \cdot N dB\)


ADC dynamic range


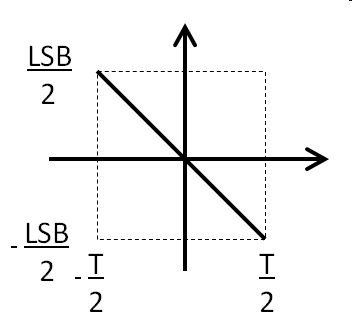
Second approximation:

\( SQNR = 6.02 \cdot N dB + 1.76 dB \)

Using integral over quantization error function.
\( \overline{\epsilon_{q}^2} = \frac{1}{T} \int_{- \frac{T}{2}}^{+\frac{T}{2}} ( k \cdot t )^2 dt \)

Root mean square value for quantization error is calculated with the integral over one period T, when the quantization error goes from \( +\frac{T}{2} \) to \( -\frac{T}{2} \):
\( \overline{\epsilon_{q}^2} = \frac{1}{T} \int_{- \frac{T}{2}}^{+\frac{T}{2}} ( k \cdot t )^2 dt \)
with \( k = - \frac{LSB}{T} \) giving \( T = - \frac{LSB}{k} \):
\( \overline{\epsilon_{q}^2} = - \frac{k}{LSB} \int_{+ \frac{LSB }{2 \cdot k}}^{- \frac{LSB}{2 \cdot k}} ( k \cdot t )^2 dt = - \frac{k^3}{LSB} \left( - \frac{LSB^{3}}{8 \cdot 3 \cdot k^3} - \frac{LSB^{3}}{8 \cdot 3 \cdot k^3} \right) = \frac{LSB^2}{12}\)
\( \epsilon_{q} = \frac{LSB}{\sqrt{12}} \)

\( SQNR = 20 \cdot log \frac{\frac{1}{\sqrt{2}} \frac{LSB \cdot 2^{N}}{2}}{\frac{LSB}{\sqrt{12}}} dB = 20 \cdot log \frac{\sqrt{12}\cdot 2^{N}}{2 \cdot \sqrt{2}} dB \)
\( SQNR = 20 \cdot log \left( 2^{N} \sqrt{\frac{3}{2}} \right) dB = N \cdot 20 \cdot log (2) dB + 20 \cdot log \left( \sqrt{\frac{3}{2}} \right) dB \)

\( SQNR = 6.02 \cdot N dB + 1.76 dB \)

Signal to Quantization noise

Signal to Quantization Noise Ratio:

\( SQNR = 6.02 \cdot N dB + 1.76 dB \)

Signal to noise and distortion ratio:
SINAD
without distortion:

SINAD = SQNR = 6.02 N dB + 1.76 dB

Effective Number of Bits:

\( ENOB = \frac{SINAD - 1.76 dB}{ 6.02 dB} \)

NSQNR [dB]
8 50
12 74
1698
20122

Die Grafik zeigt ein Sinussignal mit einer Amplitude von 128 und einer Auflösung von 8 Bit.
Führt man eine FFT mit NFFT = 256 Punkten durch ergibt sich ein Wert von

\( A_{signal} = 20 \cdot log_{10}(\frac{128}{\sqrt{2}}) = 39 dB \)

Man erwartet ein SQNR = 6.02 * 8 dB + 1.76 dB = 49.78 dB

Das wäre ein Rauschpegel von - 10.78 dB (Grüne Linie).

Dieses Rauschen wird auf alle dargestellten Frequenzen (128 = 256 / 2) aufgeteilt.

\( v_{Ges} = \sqrt{N \cdot v_i } \)

\( dA_{NFFT} = 20 \cdot log_{10} \left(\sqrt{\frac{NFFT}{2}}\right) = 10 \cdot log_{10}\left(\frac{NFFT}{2}\right) = 21 dB \)

Das Rauschen der einzelnen Frequenzen liegt dann in etwa bei -31 dB (Rote Kurve).
Bei der logarithmischen Darstellung der Frequenz liegen die Punkte der höheren Frequenzen dichter zusammen. In der Darstellung sieht man eine starke Schwankung der einzelnen Werte.
Eine Ablesung des Signal-Rausch Verhältnisses aus der Graphik ist deshalb nicht sinnvoll.
Der Signal-Rausch Abstand muss numerisch berechnet werden.

Data converter classification

  • Nyquist rate:


    fsignal < fsampling/2
    Basic ADC circuits

  • Oversampling:


    fsignal << fsampling/2
    High resolution AD converters
    Limited analog circuit complexity, higher stability concerns, high digital signal processing effort

  • Undersampling (sub-sampling):


    fsignal > fsampling/2
    Wireless, software defined radio
    Analog filter limits the band of interest

FFT simulator

The JavaScript simulator can be used:
ADCharacteristic
8-bit ADC, 0.5 V Amplitude, 0.5 V offset, 17 periods, 4096 points FFT.
Lowest frequency shows in this simulation DC magnitude.
Signal magnitude is -9 dB for frequency 17: 500 mV amplitude gives \( 20 \cdot log \left( \frac{0.5}{\sqrt{2}} \right) = -9 dB \)
Total noise is -58 dB which is -9 dB - 6.02*8 dB -1.76 dB = -58 dB using 8 bits.
Since the noise is distributed over 4096 bins the noise is distributed around:
-58 dB - 10 log (2048) dB = -91 dB.
Unfortunately there is a lot of noise, so it is difficult to estimate the -91 dB.


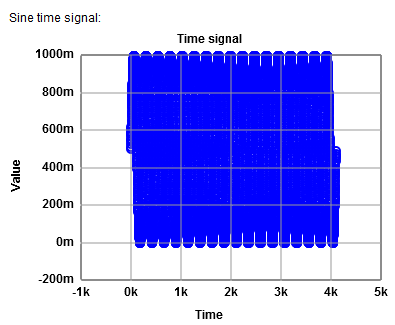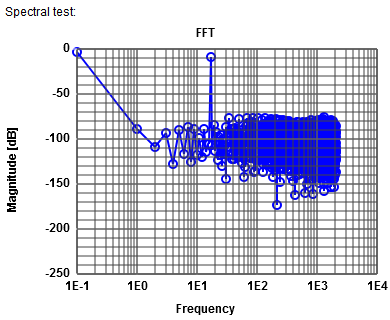Experiments using 8 bits resolution:
16 times the number of ADC levels are used as number of samples for FFT.
28 · 16 = 4096 samples for FFT.

Aliasing

- Number of periods 4096+17 = 4113

Bleeding

- Non integer number of periods shows bleeding.

Windowing

- Windowing reduces bleeding. The signal peak is distributed over some bins and the magnitude a little reduced.

Noise pattern

- Non prime integer number of periods shows noise pattern.

DNL, INL and spectral analysis

Errors: Sine amplitude 0.01 is 1 %. It is expected to loose more than 1 bit.
INL is -2.5 and could be centered.
FFT without windowing shows a signal level at fsignal of -9 dB and a harmonic at 2 fsignal with -48 dB.
This gives an ENOB of (-9 dB - (-48 dB) - 1.76 dB) / 6.02 dB = 6 bits.

White noise

A noise of 0.01 shows no clear steps in the transfer characteristic any more.
As expected the random INL will vary with every simulation run. Maximum absolute INL is around 3.
FFT without windowing shows a signal level at fsignal of -9 dB and a total noise level of -34 dB.
This gives an ENOB of (-9 dB - (-34 dB) - 1.76 dB) / 6.02 dB = 4 bits.

Single distortion in INL, DNL

What happens with the error, if there is one bad conversion.
8 bits and 17 periods simulation.
Distortion start 0.49, distortion length 0.0036 and distortion amplitude of 0.004.
INL and DNL is 0.9 LSB. Noise floor is 58.13 dB compared to 58.23 dB.
Distortion start 0.49, distortion length 0.0078 and distortion amplitude of 0.01.
From INL and DNL the value of -2 LSB is critical. Noise floor is 56.88 dB compared to 58.23 dB.
Very precise INL, DNL and FFT measurements are needed to catch missing codes.

Amplitude modulation

Windowing is like amplitude modulation spreading the power:
ω is ω + δ and ω - δ

Zusammenfassung und nächste Vorlesung


  • DNL, INL Berechnung
  • SNR Berechnung
  • Nyquist, Oversampling, Undersampling
DAC7565 2021 (1 Stk 11.- Euro, ab 2000 Stk 6.- Euro)
NBit, fs, settling time, INL, DNL,
Bipolar operation
ADS5204 2021 (1 Stk. 14.- Euro)
INl, DNL

Nächstes Mal