Elektronik 319 DatenwandlerProf. Dr. Jörg Vollrath18 Übung 3 |

|
Video der 14. Vorlesung 5.5.2021
|
Länge: 1:02:43 |
0:0:0 Schaltregler 0:1:37 5.17 Simple Buck Converter 0:3:18 Schaltfrequenz, Periodendauer, Duty Cycle 0:7:2 Schaltungsanalyse 0:8:22 Spulenstrom und Spannung 0:9:48 Signalverlauf 0:13:26 Ansatz Spannungsverhältnis 0:14:38 Spannungsverhältnis und Duty Cycle 0:16:18 LTSPICE Schaltbild (Falsche Diode) 0:18:28 Einschwingvorgang 0:20:18 Nur bei größerem Strom CCM 0:24:22 Wirkungsgrad (mit falscher Diode zu klein) 0:28:18 Ergebnis ohne Leistung an der Diode 0:31:18 Continous conduction mode CCM, Discontinous conduction mode 0:34:18 Mindeststrom Iamin für CCM 0:38:5 Ergebnis Iamin= T/2/L Ua (1 - Ua / Ue) 0:39:18 Dimensionierung L = T / 2 / Iamin Ua (1 - Ua / Ue) 0:44:8 Welligkeit dUa 0:49:18 Faktor 4 oder 8 mit Tietze Schenk 0:54:38 Faktor 8 0:56:18 Kapazitätsdimensionierung für dUa 0:58:23 Welligkeit 30 mV, T = 4 us, L = 18 uH, Ue =12 V, Ua = 6 V 1:0:48 Iamin Rechnung 1:1:58 C = 10 uF 1:4:48 LT3570 Beipielsimulation 1:8:18 Power on sequence 1:9:48 Zu niedrige Ausgangsspannung wegen R8, Ri = 1 Ohm an der Eingangsspannung |
Übersicht
- Übersicht elektronische Schaltungen
- Digitale und analoge Signale
- Digital-Analog-Wandler
- Analog-Digital-Wandler
- LSB, MSB, Nbit, Vref, Vmax, VFS, Voffset, gain error
Analog Digital Interface Circuits
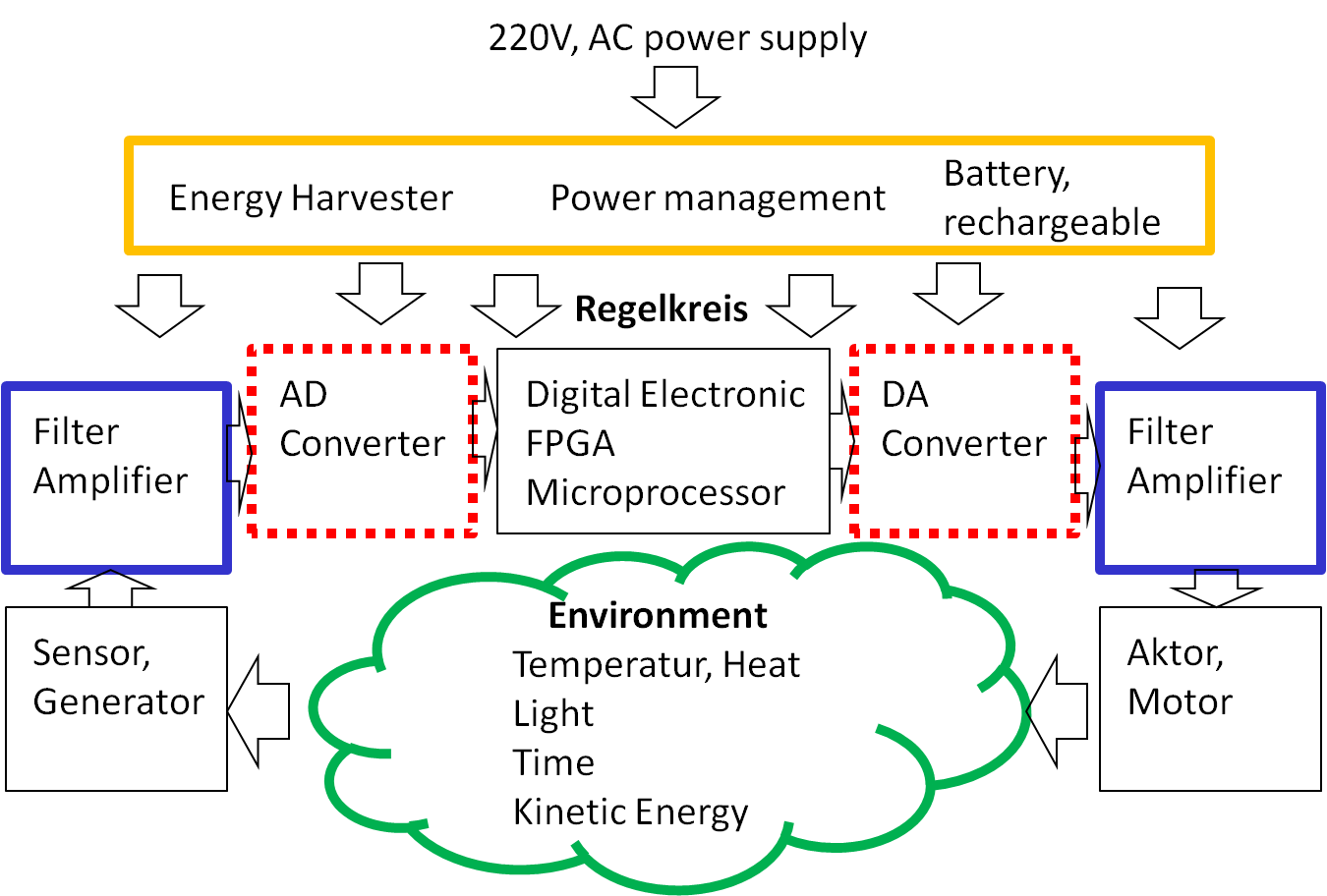
- Naturally occuring signals are analog
- Why are data converters and digital signal processing used?
FPGA embedded system
|
  |
Hier wird ein FPGA board von Digilent für etwa 120.- Euro (2023) als embedded System gezeigt. FPGAs erlauben es viele taktgenaue Funktionen parallel zu relaisieren, da sehr viele Anschlüsse zur Verfügung stehen, die einzeln programmiert werden können.
Hier werden die Anschlüsse für 18 Schiebeschalter, 18 LEDs, eine vierstellige 7-Segment Anzeige, 4 PMOD Anschlüsse (mit jeweils 8 programmierbaren Pins), Videoausgang und USB Anschluss verwendet.
Mikrocontroller Embedded System
|
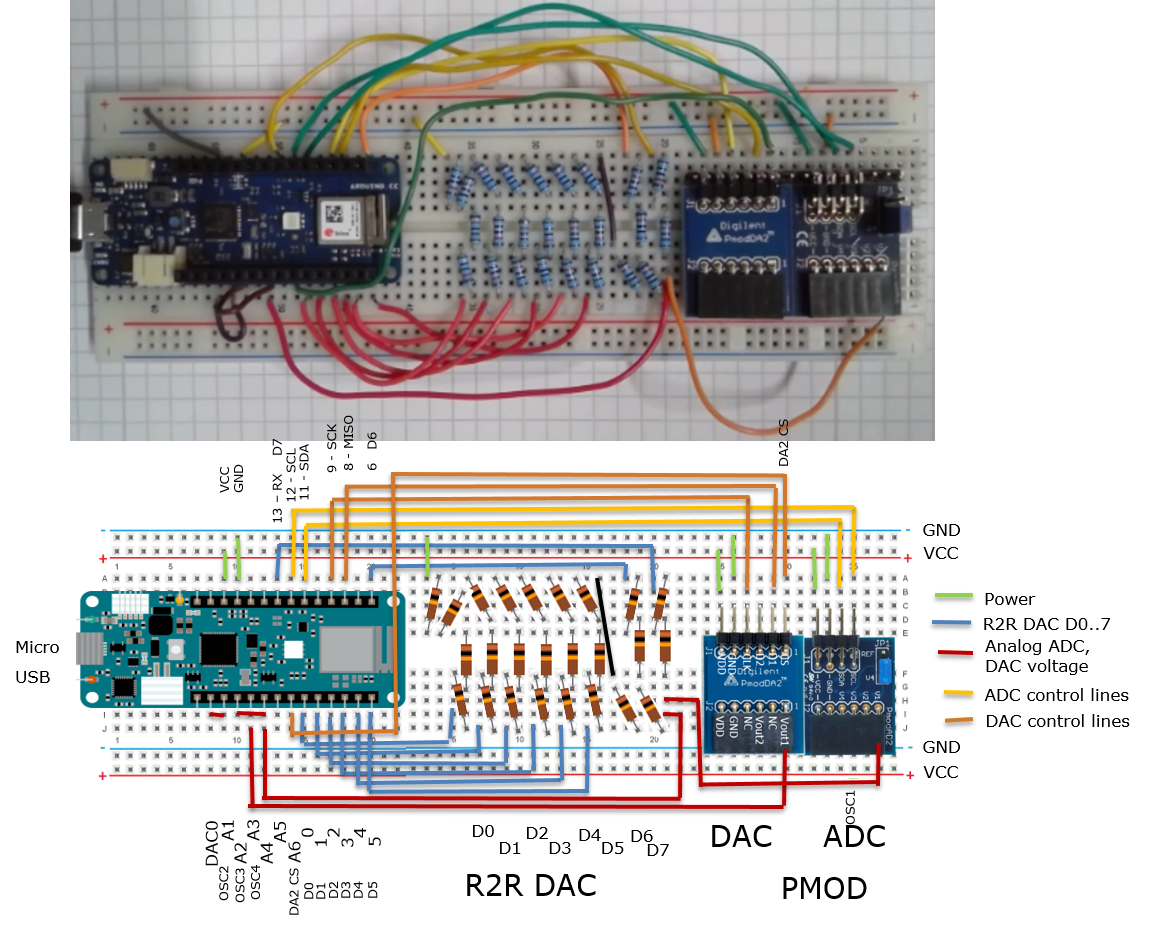
|
Hier wird ein Arduino MKR WIFI 1010 Mikrocontroller Board gezeigt (27.- 2023). Ausserdem wird ein R2R DAC realisiert, ein DAC DA2 PMOD (20.-) und ein ADC AD2 PMOD (20.- 2023) sind via SPI und I2C Schnittstelle angeschlossen.
Eine Programmierung in C erlaubt eine schnellere Entwicklung einer Applikation, die nur Zeitabläufe mit Genauigkeiten im ms Bereich möglich macht.
PMOD DA2 ( 2 Channel, 12-Bit, 125kHz, 8 µs)
Digilent: PMOD DA2 20.-
Texas Instruments DAC121S101 8us settling 12-Bit 16.5 MS/s $1.-
30 MHz SCLK
PMOD AD2
Digilent: PMOD AD2 20.-
Analog devices AD7991 4 channel, I2C, 1us conversion time, 12-bit
Properties of digital signals
Properties:
|
|
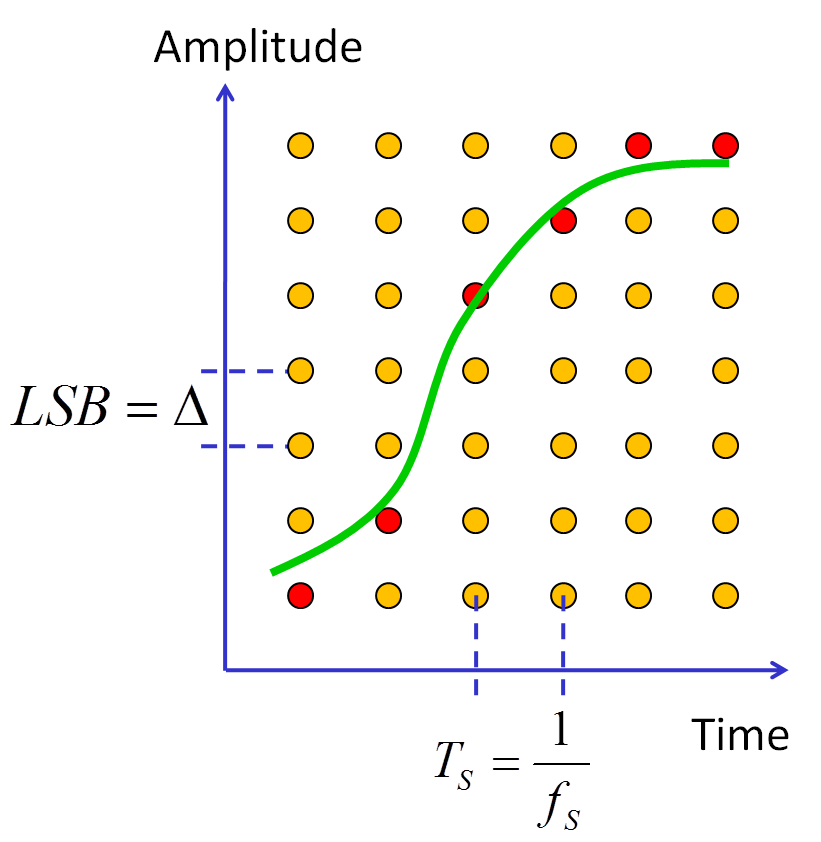
The green analog curve is discretized in time and level resulting in the red points.
The smallest difference in level is called delta Δ or LSB (least significant bit).
The smallest difference in time is called sampling time (ts).
The smallest difference in level is called delta Δ or LSB (least significant bit).
The smallest difference in time is called sampling time (ts).
Digital to analog converter metric
|
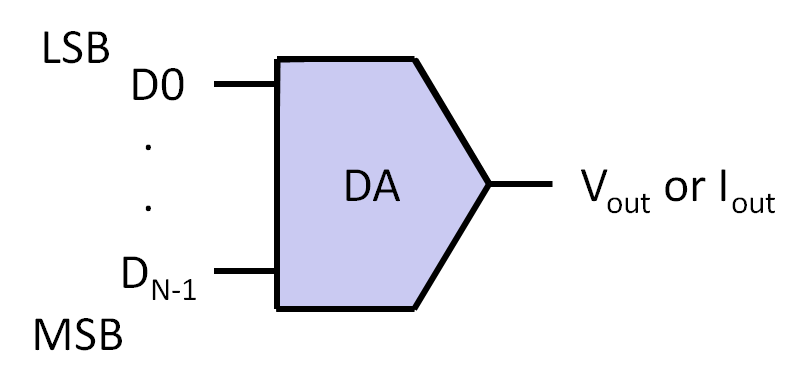 \[ \Delta = LSB = \frac{V_{ref}}{2^{Nbit}} \]
\[ N_{bit} = log_2 \frac{V_{ref}}{\Delta} = ld \frac{V_{ref}}{\Delta} \]
\[ V_{max} = V_{ref}- \Delta \]
\[ \Delta = LSB = \frac{V_{ref}}{2^{Nbit}} \]
\[ N_{bit} = log_2 \frac{V_{ref}}{\Delta} = ld \frac{V_{ref}}{\Delta} \]
\[ V_{max} = V_{ref}- \Delta \]
|
\[ V_O = V_{ref} \sum_{i=0}^{Nbit-1} \frac{D_{i}}{2^{Nbit-i}} \] \[ V_O = \Delta \sum_{i=0}^{Nbit-1} D_{i} \cdot 2^{i} \]
LSB and Digital to analog example
Es gibt das absolute Least Significant Bit (LSB) und das relative LSB.
\( LSB_{abs} = \frac{Vref}{2^{NBits}} \)
\( LSB_{rel} = \frac{1}{2^{NBits}} \)
Man rechnet einen Spannungswert in einen binären Code um, den man an den DAC anlegt.
Binary weighted inputs:
\( V_O = V_{ref} \sum_{i=0}^{Nbit-1} \frac{D_{i}}{2^{Nbit-i}} = \Delta \sum_{i=0}^{Nbit-1} D_{i} \cdot 2^{i} \)
Beispiel: LSBabs = 12 mV, Uout = 1.430 V
Welche Maximalspannung kann ein 10-Bit Wandler mit diesen Daten ausgeben?
Wie gross ist Vref?
Welche Dezimalzahl und Binärcode benötigt der DAC zur Erzeugung von Uout?
Nbit = 10
Vmax = LSB · (2Nbit - 1) = 12 mV * 1023 = 12.276 V
Vref = LSB · 2Nbit = 12 mV * 1023 = 12.288 V
Code = 1.430V / 12 mV = 119.1667
Eine ganze Zahl wird benötigt: 119
Es wird eine Spannung von 119 * LSB = 1.428 V ausgegeben.
Umwandlung Dualzahl:
Dualzahl Teilen durch 2, oder Hexadezimalzahl mit Teilen durch 16 und Umwandlung in Dual
Theorie Zahlenumwandlung
Zahlenumwandlung
119 : 2 = 59 Rest 1 LSB
59 : 2 = 29 Rest 1
29 : 2 = 14 Rest 1
14 : 2 = 7 Rest 0
7 : 2 = 3 Rest 1
3 : 2 = 1 Rest 1
1 : 2 = 0 Rest 1 MSB
MSB 1110111 LSB
119 : 16 = 7 Rest 7
7 : 16 = 0 Rest 7
x77 = 01110111
\( V_o = V_{ref} \cdot \left( \frac{0}{2^{7}} + \frac{1}{2^{6}} + \frac{1}{2^{5}} + \frac{1}{2^{4}} + \frac{0}{2^{3}} + \frac{1}{2^{2}} + \frac{1}{2^{1}} + \frac{1}{2^{0}} \right) \)
\( V_o = LSB_{abs} \cdot \left( 0 \cdot 2^{7} + 1 \cdot 2^{6} + 1 \cdot 2^{5} + 1 \cdot 2^{4} + 0 \cdot 2^{3} + 1 \cdot 2^{2} + 1 \cdot 2^{1} + 1 \cdot 2^{0} \right) \)
Vmax = LSB · (2Nbit - 1) = 12 mV * 1023 = 12.276 V
Vref = LSB · 2Nbit = 12 mV * 1023 = 12.288 V
Code = 1.430V / 12 mV = 119.1667
Eine ganze Zahl wird benötigt: 119
Es wird eine Spannung von 119 * LSB = 1.428 V ausgegeben.
Umwandlung Dualzahl:
Dualzahl Teilen durch 2, oder Hexadezimalzahl mit Teilen durch 16 und Umwandlung in Dual
Theorie Zahlenumwandlung
Zahlenumwandlung
119 : 2 = 59 Rest 1 LSB
59 : 2 = 29 Rest 1
29 : 2 = 14 Rest 1
14 : 2 = 7 Rest 0
7 : 2 = 3 Rest 1
3 : 2 = 1 Rest 1
1 : 2 = 0 Rest 1 MSB
MSB 1110111 LSB
119 : 16 = 7 Rest 7
7 : 16 = 0 Rest 7
x77 = 01110111
\( V_o = V_{ref} \cdot \left( \frac{0}{2^{7}} + \frac{1}{2^{6}} + \frac{1}{2^{5}} + \frac{1}{2^{4}} + \frac{0}{2^{3}} + \frac{1}{2^{2}} + \frac{1}{2^{1}} + \frac{1}{2^{0}} \right) \)
\( V_o = LSB_{abs} \cdot \left( 0 \cdot 2^{7} + 1 \cdot 2^{6} + 1 \cdot 2^{5} + 1 \cdot 2^{4} + 0 \cdot 2^{3} + 1 \cdot 2^{2} + 1 \cdot 2^{1} + 1 \cdot 2^{0} \right) \)
Digital to analog converter transfer characteristic
|
Vref = 2 V Table: Ideal 2-bit DAC
|
\( LSB = \frac{V(11)-V(00)}{2^{Nbit}-1} \)
Offset error: Voffset = V(00) = 0.2 V
Gain error: Vgain = \( \frac{V(11)_{real} }{ V(11)_{ideal} } = 1.1 \)
The points are the generated measurable values. The straight line only interpolates these values to show a
linear relationship of the values.
DAC sine signal
|
U(t) = A · sin(ωt) Erzeuge Codes für positive ganze Zahlen: \( A = \frac{2^{Nbit} - 1}{2} \) U(t) = Runde( A · ( 1 + sin(ωt))) Erzeugung mit festem Zeitraster tCLK
|
Je nach Anzahl von Messpunkten und Perioden werden nicht alle möglichen
Ausgangscodes verwendet.
Wenn die Anzahl der Perioden größer ist als die halbe Anzahl der Punkte sieht man Aliasing.
Punkte 16: Periode 1, sieht genauso aus wie Periode 15, 17, 31, 33 ..
Man spricht von Nyquistzonen und undersampling.
Es wird meist eine Tabelle verwendet, da die Sinusberechnung zu lange dauert.
Spezielle Hardware implementiert eine Sinusberechnung mit Reihenentwicklung.
Komplexe Rechnung kann auch verwendet werden.
Wenn die Anzahl der Perioden größer ist als die halbe Anzahl der Punkte sieht man Aliasing.
Punkte 16: Periode 1, sieht genauso aus wie Periode 15, 17, 31, 33 ..
Man spricht von Nyquistzonen und undersampling.
Es wird meist eine Tabelle verwendet, da die Sinusberechnung zu lange dauert.
Spezielle Hardware implementiert eine Sinusberechnung mit Reihenentwicklung.
Komplexe Rechnung kann auch verwendet werden.
#define HWORDS 1024 // Buffer length should be 4 * NCODE to excercise all codes
#define NCODE 256 // Number of codes 2^8
volatile uint16_t sintable1[HWORDS];
volatile uint16_t periods;
for (uint16_t i = 0; i < HWORDS; i++) // Calculate the sine table with HWORDS entries
{
sintable1[i] = (uint16_t)((sinf(2 * PI * (float)i / (float)HWORDS) + 1) / 2 * (NCODE-1) );
}
periods = 1; // number of periods (odd number) per HWORDS samples
for (uint16_t i = 0; i < HWORDS; i++) // Step through sintable array
{
Outputvalue = sintable1[ (i * periods) % HWORDS];
}
Beispiel: DAC
|
Datenblatt des Mikrocontrollers Vref=3.3V Nbit = 10 Berechnen Sie die kleinste Schrittweite. Mit welcher Genauigkeit muß die Schrittweite angegeben werden? Welcher Code wird für 2.000 V Ausgangsspannung benötigt. Wie groß ist die Ausgangsspannung wirklich? |
\( LSB_{abs} = \frac{3.3 V}{1024} = 3.222656 mV \)
4 gültige Ziffern: 3.223 mV
3.22 mV * 1024 = 3.297 V
Die Abweichung vom Wert 3.3 ist 3 mV, etwa 1 LSBabs.
\( \frac{V_{out}}{LSB_{abs}} = \frac{2.000 V}{3.222656 mV} = 620.54 \)
Man nimmt 621 und bekommt:
2.0015 V
Kalibrierung
Jeder DAC und ADC muss in regelmäßigen Zeitabständen kalibriert werden.Zur Kalibrierung wird die Spannung beim minimalen Code (Cmin = 00..00) gemessen V(Min) und die Spannung beim maximalen Code (Cmax = 11..11) V(Max).
\( LSBreal = \frac{V(Max) - V(Min)}{Cmax - Cmin} \)
Für eine Ausgangsspannung lautet die Gleichung dann:
\( Code = Runde \left( \frac{Vout - V(Min)}{LSBreal} \right) + Cmin \)
AD Converter Metric
|
Nbit: Number of Bits D0..DN-1: Binary weighted data lines Vin: Positiv input voltage Vmax: Maximum input voltage VFS: Full scale voltage Vref: Reference voltage Δ = LSB: minimum resolvable input For small Nbit there is a significant difference LSB or Δ between Vmax, VFS and Vref. In general \( V_{max} = V_{FS} = V_{ref} - LSB \) (Baker). For large Nbit, LSB gets small and Vmax = VFS ≈ Vref. |
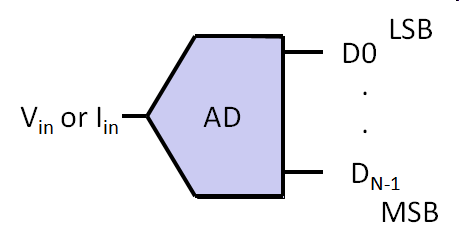 Ideal analog-to-digital converter An analog voltage or current is transfered into a digital output. Input range is positiv. Uniform, binary digital encoding |
AD Transfer Characteristic
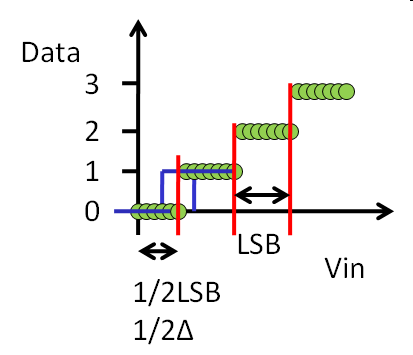 Transition depends on measurement accuracy and step size. |
Vref = 1V Nbit = 2 LSB = 0.25V Upper voltage limit (transition voltage) for a digital output code:
|
Analog-Digital-Converter (ADC)
Nbit: Number of bits
Vref: Reference voltage
Example: N = 12, Vref = 4 V
\( LSB_{rel} = \frac{1}{2^{12}} = \frac{1}{4096} = 0.00024414 = 244.14 ppm \)
\( LSB_{abs} = \frac{4 V}{2^{12}} = \frac{4 V}{4096} = 976.56 uV \)
We are using LSBabs.
Attention rounding of LSB:
4095 * 976.56 uV = 3.999 V
4095 * 976 uV = 3.996 V
3 mV Difference in calculation versus LSBabs 0.976 mV
Kalibrierung
Man misst bei einer sehr hohen Spannung Vmax den maximalen Code Cmax.Man misst bei einer sehr niedrigen Spannung Vmin den minimalen Code Cmin.
Man berechnet LSBreal:
\( LSB_{real} = \frac{V(Max) - V(Min)}{Cmax - Cmin} \)
Man berechnet die Spannung:
Vreal = (Cout - Cmin) * LSBreal + Vmin
Static Errors
|
Offset Error, Gain Error Offset and gain error will be fixed during manufacturing. A trimmable amplifier is used. In this lecture first the LSB or Δ is calculated from the first and last points of the transfer curve. Then the offset is calculated for the first code or first transition voltage. Then static errors differential non linearity (DNL) and integral non linearity (INL) are calculated. |
\( LSB = \frac{ V_T (10/11)_{real} - V_T (00/01)_{real}}{2^{Nbit}-2} \)
Offset error: Voffset = VT(00/01) - 0.5 LSB = - 0.2 V
Gain error: \( V_{gain} = \frac{V_T (10/11)_{real} }{ V_T (10/11)_{ideal} } = 0.9 \)
Beispiel: ADC Multimeter
|
Das links abgebildete Multimeter ist zu sehen. Was ist die benötigte Anzahl Bits für die Einstellung V 2000m? Berechnen Sie LSBreal und LSBrel. Mit welcher Genauigkeit muß die Schrittweite angegeben werden? Wieviel Bits kann ein DAC haben, dem man mit diesem Multimeter misst? |

|
Maximum Code: 1999
Minimum Code: -1999
Anzahl codes: 3999
NBit = log2 3999 ≈ 12 Bit
\( LSB_{rel} = \frac{1}{4096} = 0.000244 = 244.14 ppm \)
\( LSB_{abs} = \frac{4 V}{4096} = 0.9765625 mV \)
0.976 mV * 4096 = 3997.696 mV
0.9765 mV * 4096 = 3999.744 mV
0.97656 mV * 4096 = 3999.989 mV
Mit 4 gültigen Stellen ist der Fehler am Ende kleiner als 0.5 LSB.
Das messende Multimeter muss mehr Bits haben, als der zu messende DAC (Device under Test: DUT).
Nbit,DACmax ≈ Nbit,test - 4
Minimum Code: -1999
Anzahl codes: 3999
NBit = log2 3999 ≈ 12 Bit
\( LSB_{rel} = \frac{1}{4096} = 0.000244 = 244.14 ppm \)
\( LSB_{abs} = \frac{4 V}{4096} = 0.9765625 mV \)
0.976 mV * 4096 = 3997.696 mV
0.9765 mV * 4096 = 3999.744 mV
0.97656 mV * 4096 = 3999.989 mV
Mit 4 gültigen Stellen ist der Fehler am Ende kleiner als 0.5 LSB.
Das messende Multimeter muss mehr Bits haben, als der zu messende DAC (Device under Test: DUT).
Nbit,DACmax ≈ Nbit,test - 4
LTSPICE: Scalable behavioral 4 Bit DAC
|
Behavioral voltage source BV with equation V=V(in1)/16+V(D3)/2+V(D2)/4+V(D1)/8+V(D0)/16 Scalable DAC takes input signal In1 as high resolution input and adds D3..D0 information. For high resolution more modules can be combined. The digital input for a sine signal can be easily generated with a behavioral ADC with a sine source as input. |
LTSPICE: Scalable behavioral 4 Bit ADC
|
Behavioral voltage source BV Rounding function: V(D3) = round(V(IN)) V(D2) = round(V(IN)*2-V(D3)) ... Residue: V(Out) = V(in)*16-V(D3)*8-V(D2)*4-V(D1)*2-V(D0) Residue allows extending the ADC for high resolution. A sample and hold circuit at the input can be seen. |
LTSPICE: Test for 4 Bit ADC and DAC
|
A 4 Bit ADC and DAC test can be simulated in LTSPICE. The output file size can be limited by using the .save dialog option. The output shows the step size of the digitalisation. 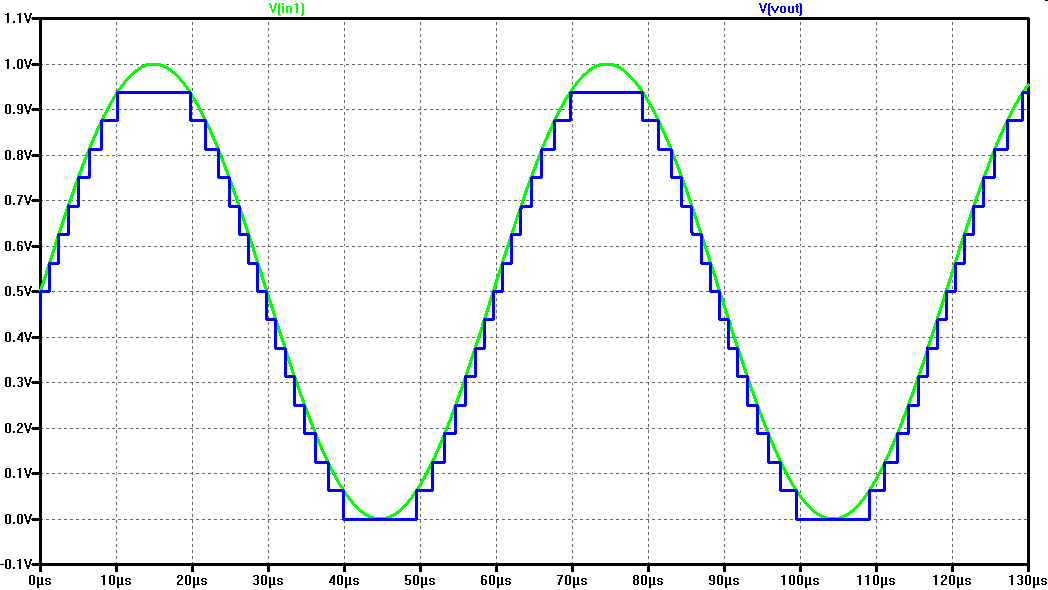
|
Zusammenfassung und nächste Vorlesung
- Unterschied zwischen analogen und digitalen Signalen
- Parameter für Datenwandler
LSBabs, LSBrel, Δ, fs, Ts, Di, MSB, Vout, Nbit, Vref, Vmax, VFS, Voffset, gain error
Nächstes Mal