Übersicht, Lernziele
- Spezifischer Widerstand und spezifische Leitfähigkeit
- Materialien für Leiter
- Widerstand, Material und Geometrie
- Temperaturabhänigkeit von Widerständen
Ein ohmscher Widerstand wird durch das verwendete Material und die Geometrie bestimmt.
Der Widerstand ändert sich meist mit der Temperatur.
Der Widerstand ändert sich meist mit der Temperatur.
Spezifischer Widerstand und Leitfähigkeit
\( \left[\kappa\right]= \frac{1}{\Omega m} = \frac{S}{m} \frac{A}{V m} \) |
|
Ein Widerstand ergibt sich aus einem leitendem Material mit einem Querschnitt A und einer Länge l.
Jedes Material hat einen spezifischen Widerstand.
In der Elektrotechnik wird Kohlenstoff oder Kupfer, Aluminium als Leiter und Widerstand eingesetzt.
Jedes Material hat einen spezifischen Widerstand.
In der Elektrotechnik wird Kohlenstoff oder Kupfer, Aluminium als Leiter und Widerstand eingesetzt.
Praxisbezug Widerstand
|
|
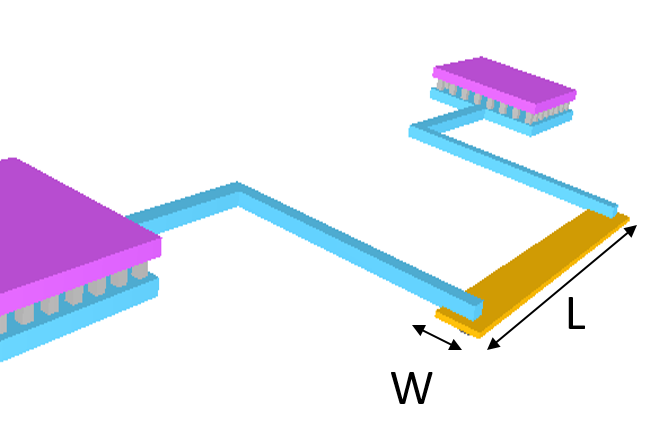
Das obere Bild zeigt eine Mikroskopaufnahme eines integrierten Widerstandes.
In der Mitte ist eine horizontale dotierte Widerstandsbahn zu sehen, die
rechts und links an Metallbahnen angeschlossen ist.
Im unteren Bild ist diese Struktur mit einer Weite W und einer Länge L
schematisch in einer 3D Ansicht zu sehen.
Tabelle spezifischer Widerstand bei 20 °C
| Material | Spezifischer Widerstand / Ω m |
Temperaturkoeffizient α20 / K-1 |
| Aluminium (Al) | 0.0278 · 10 -6 | 3.9 · 10 -3 |
| Eisen (Fe) | 0.1..0.15 · 10 -6 | 5.6 · 10 -3 |
| Kupfer (Cu) | 0.0176 · 10 -6 | 3.9 · 10 -3 |
| Konstantan | 0.5 · 10 -6 | 5 · 10 -5 |
| Silizium (Si) | 2.3 · 10 3 | -75 · 10 -3 |
| \( X(T) = X(T_{0}) \left(1 + \alpha (T - T_{0}) \right) \) |
T0 Bezugstemperatur
α Temperaturkoeffizient
Quelle:??
Eine temperaturabhängige Größe wird näherungsweise durch ein lineares Modell beschrieben.
Eine temperaturabhängige Größe wird näherungsweise durch ein lineares Modell beschrieben.
Beispiel: Widerstandsberechnung
Bestimmen Sie den Widerstand eines 1 m langen Kupferdrahtes mit einem Durchmesser von 1 mm bei Raumtemperatur.
Wie groß ist der Spannungsabfall an diesem Widerstand, wenn ein Strom von 100 mA fliesst?
Die Formel lautet:
\( R = \frac{\rho l}{A} \)
ρ liest man für Kupfer aus der Tabelle ab:
\( \rho = 0.0176 \cdot 10^{-6} \Omega m \)
l = 1 m
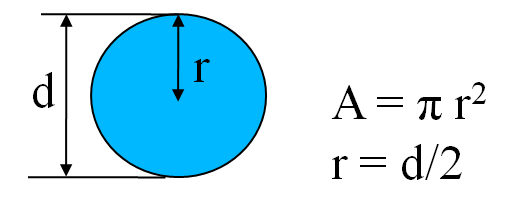
\( A = \pi r^2 = \pi \left( \frac{d}{2}\right)^2 = 3.14 \left( \frac{1 \cdot 10^{-3} m}{2}\right)^2 = 3.14 \cdot 0.25 \cdot 10^{-6} m^2 = 7.85 \cdot 10^{-7} m^{2}\)
\( R = \frac{\rho l}{A} = \frac{0.0176 \cdot 10^{-6} \Omega m 1 m}{7.85 \cdot 10^{-7} m^{2}} = \)
\( R = \frac{\rho l}{A} \)
ρ liest man für Kupfer aus der Tabelle ab:
\( \rho = 0.0176 \cdot 10^{-6} \Omega m \)
l = 1 m
\( A = \pi r^2 = \pi \left( \frac{d}{2}\right)^2 = 3.14 \left( \frac{1 \cdot 10^{-3} m}{2}\right)^2 = 3.14 \cdot 0.25 \cdot 10^{-6} m^2 = 7.85 \cdot 10^{-7} m^{2}\)
\( R = \frac{\rho l}{A} = \frac{0.0176 \cdot 10^{-6} \Omega m 1 m}{7.85 \cdot 10^{-7} m^{2}} = \)
Beispiel: Temperaturabhängigkeit eines Widerstandes
Wie ändert sich der Widerstand eines 1 m langen Kupferdrahtes mit einem Durchmesser von 1 mm, wenn sich die Temperatur von 22°C (Raumtemperatur) auf 80°C ändert?.
Wie ändert sich der Spannungsabfall an diesem Widerstand, wenn ein Strom von 100 mA fliesst?
Beispiel: Temperaturabhängigkeit eines Widerstandes
Erwärmt man einen Leiter von T1 = 20 °C auf T2 = 60 °C, so nimmt sein Widerstand um p = 0.62% zu. Wie groß ist der Temperaturkoeffizient α20 des Leitermaterials?
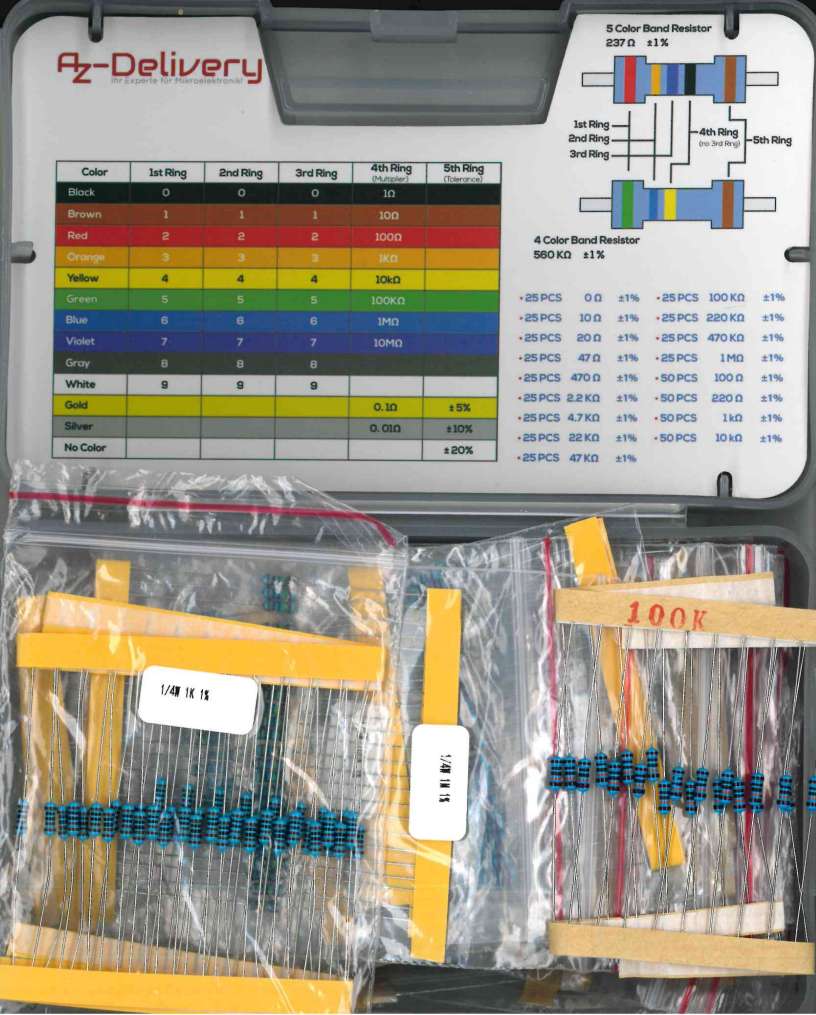
Ein Widerstandssortiment
|
Wertebereich: 10 Ω bis 1 MΩ Toleranzbereich: 10%, 1%, 0.1% Bauform: Axial (mounting through hole), SMD (surface mount devices) Maximale Leistung: 1/4 W, 1/8 W |
|
Der Widerstandswert kann mit einem Farbcode auf dem Bauteil markiert werden.
Je nach dem Toleranzbereich gibt es mehr oder weniger verschiedene Widerstandswerte.
Die Anschlussdrähte sollten einen geeigneten Durchmesser für ein Breadboard (Steckbrett) haben.
Bei einem Widerstandssortiment sollte ein gewünschter Wert schnell gefunden werden. Dies ist mit maximal 20 unterschiedlichen Werten in Fächern oder beschrifteten Tüten der Fall.
Bei kleinen Widerstandswerten kann die maximale Leistung schnell überschritten werde.
\( P = U \cdot I = U \cdot \frac{U}{R} = \frac{U^2}{R} =\frac{(5 V)^2}{10 \Omega } = 2.5 W \)
Für eine Diodenmessung werden 6 Messwiderstände für die Strommessung verwendet: 10 Ω, 100 Ω, 1 kΩ, 10 kΩ, 100 kΩ und 1 MΩ.
Je nach Messwiderstand können kleinere oder größere Ströme gemessen werden.
Je nach Widerstandswert wird bei einer festen Spannung der Strom begrenzt.
Beispiel: U = 5 V, R = 1 kΩ, \( I_{max} = \frac{U}{I} = 5 mA\)
Je nach dem Toleranzbereich gibt es mehr oder weniger verschiedene Widerstandswerte.
Die Anschlussdrähte sollten einen geeigneten Durchmesser für ein Breadboard (Steckbrett) haben.
Bei einem Widerstandssortiment sollte ein gewünschter Wert schnell gefunden werden. Dies ist mit maximal 20 unterschiedlichen Werten in Fächern oder beschrifteten Tüten der Fall.
Bei kleinen Widerstandswerten kann die maximale Leistung schnell überschritten werde.
\( P = U \cdot I = U \cdot \frac{U}{R} = \frac{U^2}{R} =\frac{(5 V)^2}{10 \Omega } = 2.5 W \)
Für eine Diodenmessung werden 6 Messwiderstände für die Strommessung verwendet: 10 Ω, 100 Ω, 1 kΩ, 10 kΩ, 100 kΩ und 1 MΩ.
Je nach Messwiderstand können kleinere oder größere Ströme gemessen werden.
Je nach Widerstandswert wird bei einer festen Spannung der Strom begrenzt.
Beispiel: U = 5 V, R = 1 kΩ, \( I_{max} = \frac{U}{I} = 5 mA\)
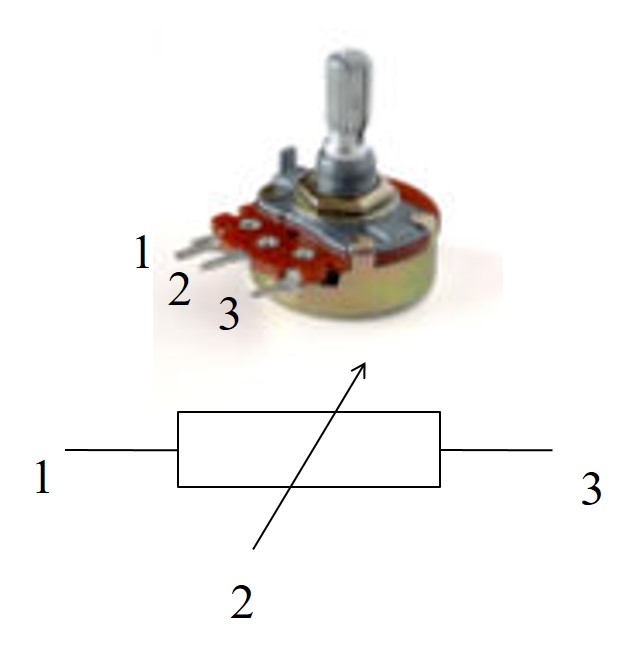
Verstellbare Widerstände: Potentiometer
|

|
Beispiel Messung des spezifischen Widerstands

|
Für die Messung wählt man eine geeignete Drahtlänge l, einen Durchmesser d für einen Querschnitt A
und einen geeigneten Messstrom.
Man verwendet einen sehr kleinen Querschnitt und eine grosse Drahtlänge.
Damit sich der Draht nicht erwärmt, sollte der Strom durch den Leiter klein sein. Durch die grosse Länge ergibt sich selbst bei kleinen spezifischen Widerständen ein messbarer Spannungsabfall.
Damit der Versuchsaufbau nicht zu gross wird, werden die Lüsterklemmen zur Verbindung genommen. Man misst eine Kombination aus Drahtwiderstand und Klemmenwiderstand.
LEIFI Physik Bestimmung des spezifischen Widerstandes
Man verwendet einen sehr kleinen Querschnitt und eine grosse Drahtlänge.
Damit sich der Draht nicht erwärmt, sollte der Strom durch den Leiter klein sein. Durch die grosse Länge ergibt sich selbst bei kleinen spezifischen Widerständen ein messbarer Spannungsabfall.
Damit der Versuchsaufbau nicht zu gross wird, werden die Lüsterklemmen zur Verbindung genommen. Man misst eine Kombination aus Drahtwiderstand und Klemmenwiderstand.
LEIFI Physik Bestimmung des spezifischen Widerstandes
Zusammenfassung
- Sie können mit dem spezifischen Widerstand oder Leitwert für eine gegebene Geometrie den ohmschen Widerstand berechnen.
- Sie können die Veränderung des Widerstandes mit der Temperatur bestimmen.
Nächste Vorlesung:
04 Reihen und Parallelschaltung
