Diese Präsentation beschäftigt sich mit dem Schaltungsentwurf.

Eine Funktion wird mathematisch beschrieben und mit einer Topologie (Anordnung von Bauelementen) und Auswahl geeigneter Bauelementeeigenschaften beschrieben.
Die Eigenschaften einer Zusammenschaltung von Quellen und Widerständen soll nicht nur mathematisch beschrieben werden.

Die mathematische Beschreibung wird durch Simulation, einen Schaltungsaufbau und eine Messung ergänzt.
Die mathematische Rechnung, die Simulation und die Messung sollen die gleichen Ergebnisse liefern.
Dieses Vorgehen bezeichnet man als Schaltungsentwurf.

Die obige Liste zeigt ausserdem die nächsten Themen und Bauelemente dieser Vorlesung: Nichtlineare Elemente und Verstärker, die in den kommenden Vorlesungen behandelt werden.

Beim Schaltungsentwurf soll ein Verhalten, das z.B. durch eine Gleichung beschrieben wird mit diskreten oder integrierten Schaltkreisen auf einer Platine in einem Gehäuse realisiert werden.
Eine typische Übertragungsfunktion, die ein elektrisches Verhalten beschreibt, ist in der Mitte abgebildet.
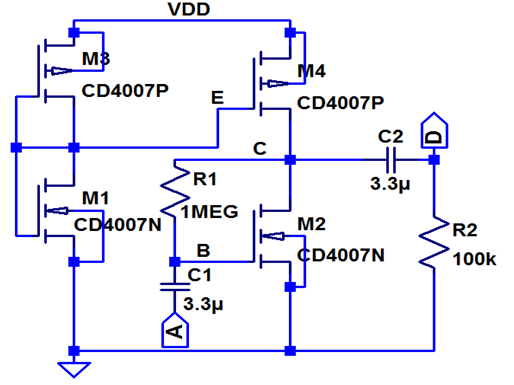
Man kann diese Übertragungsfunktion mit integrierten Schaltungen (links oben) oder einer Transistorschaltung auf einer Platine (rechts unten) realisieren. Dazu erstellt man einen geeigneten Schaltplan (links unten) und verifiziert die Funktionsweise mit einer Simulation und mit einem Steckbrettaufbau (rechts oben).
Die Abbildungen zeigen beispielhaft sehr unterschiedliche Schaltungen.
Komplexere Schaltungen realisiert man durch Zusammenschaltung von Einzelbauelementen oder Teilschaltungen.
Diese Vorlesung beschäftigt sich mit den Eigenschaften (Strom-Spannungs-Kennlinien) von Bauelementen (Widerstand, Diode, MOSFET, Operationsverstärker) und einfachen Schaltungen.

Zu jedem Schaltungsentwurf gehört ein Modell (Gleichung), eine Simulation und eine Messung einer aufgebauten Schaltung.
Eine funktionierende Schaltung wird durch Verönderungen von Bauteilen und Bauteileigenschaften oder Teilschaltungen für einen Anwendungsfall optimiert.
Dafür benötigt man das Verständnis der Gleichung, die Simulation und die Messung eines Schaltungsaufbaus.

Die Schaltung zeigt eine Spannungsquelle V1 die mit einer Reihenschaltung von R1 und R2 verbunden ist.
Die Berechnung von Spannung und Strom wird mit der Simulation und Messung verglichen.
Es fliesst ein Strom I durch R1 und R2 und es gilt das ohmsche Gesetz für den Gesamtwiderstand R = R1 + R2 und die Einzelwiderstände R2 und R1.

\( I = \frac{V_1}{R_1 + R_2} = \frac{V(C2DC)}{R_2} = \frac{V(C1DC) - V(C2DC)}{R_1} \)

\( V(C2DC) = V_1 \cdot \frac{R_2}{R_1 + R_2} = 4 V \cdot \frac{100 k\Omega}{10 k\Omega + 100 k\Omega} = 3.64 V \)
Das ist die bekannte Spannungsteilerformel.

\( I = \frac{V_1}{R_1 + R_2} = \frac{4 V}{10 k\Omega + 100 k\Omega} = 36.4 uA \)

Nach dem Herunterladen des LTSPICE Schaltplans, der Simulation und der Darstellung von V(c2dc) und I(R2) liest man mit dem Cursor die Maximale Spannung und den meaximalen strom bei V1 = 4 V ab.
Um die Ablesegenauigkeit zu vergrößern kann man in die Grafik hineinzoomen oder eine Messanweisung durchführen.

.MEAS TRAN VC2DC FIND V(c2dc) AT=0.5m
.MEAS TRAN I FIND I(R2) AT=0.5m

Im SPICE Error Log (Aktives Schaltplanfenster, 'View','SPICE Error Log') findet man

vc2dc: v(c2dc)=3.63636 at 0.0005
i: i(r2)=-3.63636e-005 at 0.0005

Nach Aufbau der Schaltung auf dem breadboard kann man eine Messung durchführen. Beim Oszilloskop aktiviert man die Berechnung des Stromes ('M1 = (C2 - C1)/1000') und die Messung der Amplitude von C2 und M1 bei einem Dreieckssignal (AWG1, Dreieck, f = 1kHz, Offset 0 V, Amplitude 4 V), wie bei der Simulation.
Die gemessenen Werte schwanken etwas (3.63 V .. 3.65 V, 36..37 uA) um die berechneten und simulierten Werte.

Die Messung und Simulation bestätigen die Rechnung.