Meine Person
|
|
Bei meiner Tätigkeit in der Industrie (1994-2010) wurden die neusten CMOS-Prozesstechnolgien für
integrierte Schaltungen (DRAMs) eingesetzt.
In CMOS Technologie wurden Ladungspumpen, Spannungsregler, PLLs und DLLs, analoge Verstärker, Referenzspannungsquellen, digitale Schaltungen und high speed Busse realisiert.
Dabei traten nur parasitäre, laterale bipolare Transistoren auf.
Das Design in einer neuen Technologie musste gleich funktionieren, da ein Maskensatz mehrere hunderttausend Euro kostet.
Die Simulation wurde zur Schaltungsentwicklung eingesetzt und musste das reale Verhalten der Schaltung möglichst genau abbilden.
Eine grosse Bedeutung hat der Test.
Für die Simulation wurden sowohl CMOS Bauelemente, als auch parasitäre Widerstände und Kapazitäten von Leitungen und Bauelementen charakterisiert.
Am Speicherchip wurden mit Hilfe von Testpunkten interne Signal gemessen und mit der Simulation verglichen.
Ausserdem wurde die Gesamtfunktionalität bei verschiedenen Spannungen und Temperaturen verifiziert. Dabei wurde auch der Herstellungsprozess variiert (Process window).
Da Millionen von Chips hergestellt wurden traten einige Fehler nur sehr selten auf 1..100 ppm und mussten dennoch reproduziert, analysiert und behoben werden, um dass Produkt erfolgreich verkaufen zu können.
In CMOS Technologie wurden Ladungspumpen, Spannungsregler, PLLs und DLLs, analoge Verstärker, Referenzspannungsquellen, digitale Schaltungen und high speed Busse realisiert.
Dabei traten nur parasitäre, laterale bipolare Transistoren auf.
Das Design in einer neuen Technologie musste gleich funktionieren, da ein Maskensatz mehrere hunderttausend Euro kostet.
Die Simulation wurde zur Schaltungsentwicklung eingesetzt und musste das reale Verhalten der Schaltung möglichst genau abbilden.
Eine grosse Bedeutung hat der Test.
Für die Simulation wurden sowohl CMOS Bauelemente, als auch parasitäre Widerstände und Kapazitäten von Leitungen und Bauelementen charakterisiert.
Am Speicherchip wurden mit Hilfe von Testpunkten interne Signal gemessen und mit der Simulation verglichen.
Ausserdem wurde die Gesamtfunktionalität bei verschiedenen Spannungen und Temperaturen verifiziert. Dabei wurde auch der Herstellungsprozess variiert (Process window).
Da Millionen von Chips hergestellt wurden traten einige Fehler nur sehr selten auf 1..100 ppm und mussten dennoch reproduziert, analysiert und behoben werden, um dass Produkt erfolgreich verkaufen zu können.
Arbeitsgebiete
Wechselgröße: Ton
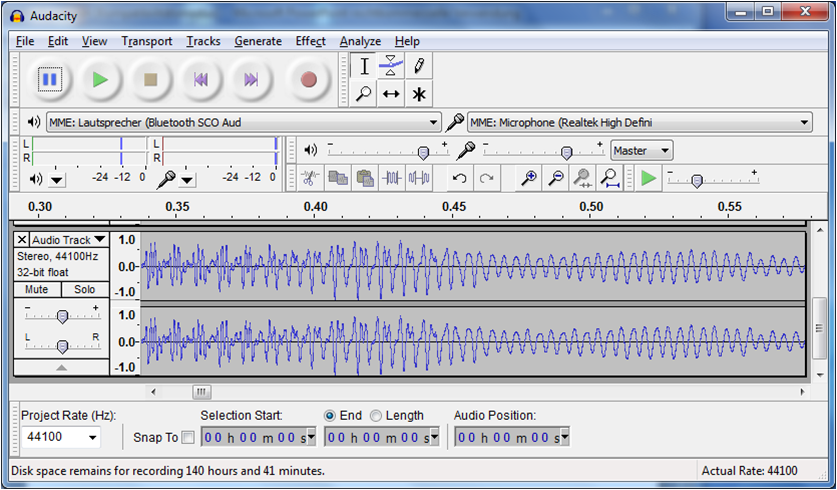
Das Bild zeigt die zeitabhängige Spannung eines Musikstückes im Programm Audacity.
Dies ist ein Beispiel für die elektrische Nachrichtenübertragung.
Man sieht eine Wechselgröße bei der eine Spannung zeitlich variiert, positive und negative Werte annehmen kann.
Eine reine Wechselgröße hat einen zeitlichen Mittelwert von Null.
Ist der zeitliche Mittelwert (Average) nicht Null liegt eine Mischgröße vor mit Wechselanteil und Gleichanteil. Der Gleichanteil wird auch als Offset bezeichnet.
Dies ist ein Beispiel für die elektrische Nachrichtenübertragung.
Man sieht eine Wechselgröße bei der eine Spannung zeitlich variiert, positive und negative Werte annehmen kann.
Eine reine Wechselgröße hat einen zeitlichen Mittelwert von Null.
Ist der zeitliche Mittelwert (Average) nicht Null liegt eine Mischgröße vor mit Wechselanteil und Gleichanteil. Der Gleichanteil wird auch als Offset bezeichnet.
Test 1
Geben Sie die charakteristischen Größen der folgenden Spannungsmessung an:
Spannungsmessung
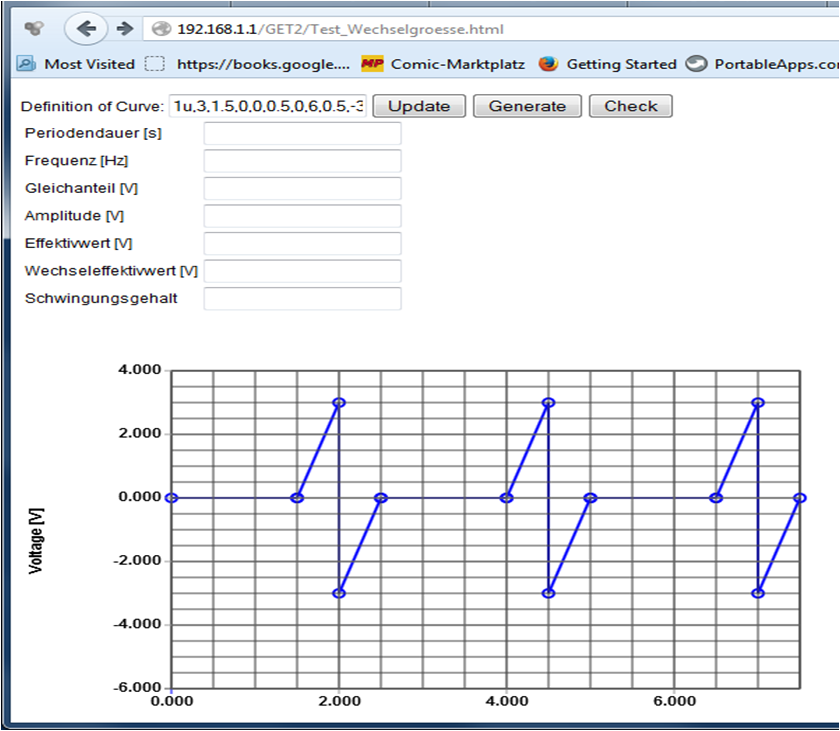
Charakteristische Größen:
Wie kann man obiges Signal beschreiben?
Was ist in dem Bild dargestellt?
Diskutieren Sie mit ihrem Nachbarn.
Wie kann man obiges Signal beschreiben?
Was ist in dem Bild dargestellt?
Diskutieren Sie mit ihrem Nachbarn.
Charakteristische Größen
|
|
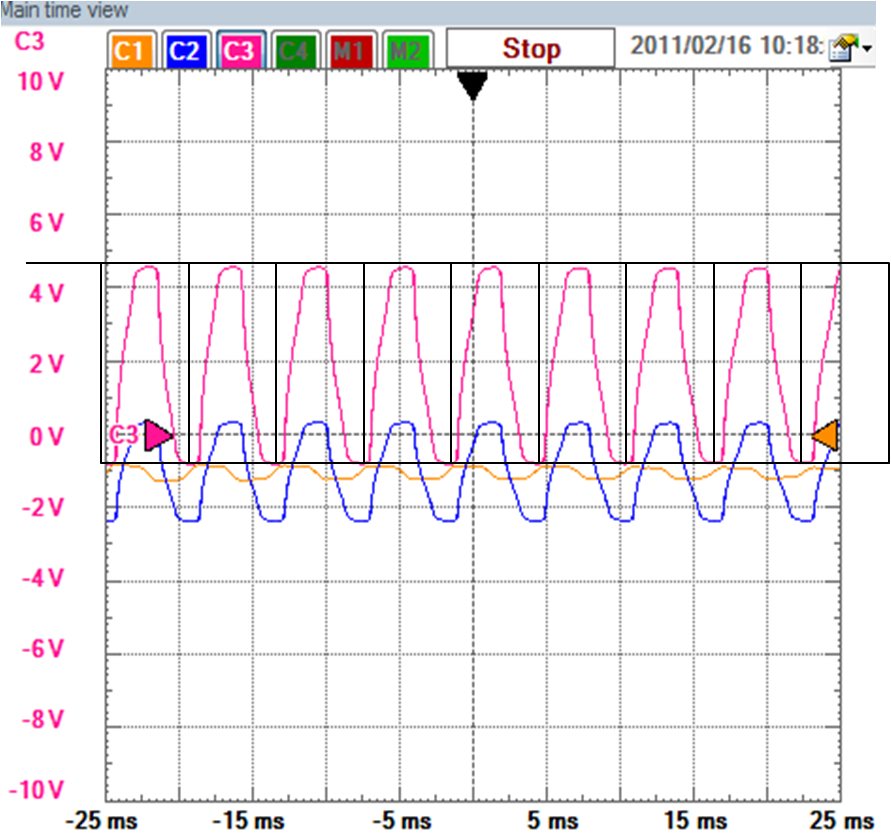
Das Signal nennt man eine periodische Schwingung.
Es kann Strom oder Spannung sein.
Der Maximalwert wird auch Scheitelwert genannt.
Die Schwingungsbreite nent man auch Spitze-Spitze-Wert (peak to peak value).
Es kann Strom oder Spannung sein.
Der Maximalwert wird auch Scheitelwert genannt.
Die Schwingungsbreite nent man auch Spitze-Spitze-Wert (peak to peak value).
Praxisbezug: Oszilloskop
Aufnahme schneller periodischer SignaleDie Triggereinheit bewirkt dabei, dass die Kurven immer ab dem selben Zeitpunkt aufgenommen werden.
→ Oszilloskop
Jedes Oszilloskop hat 3 Bereiche zur Einstellung vom
- Trigger
- der Zeitbasis (Time, x-Achse, horizontal)
- und für jeden Kanal einzeln des Eingangsbereiches (Vertical, y-Achse).
Praxisbezug: Oszilloskop
Aufnahme schneller periodischer SignaleDie Triggereinheit bewirkt dabei, dass die Kurven immer ab dem selben Zeitpunkt aufgenommen werden.
→ Oszilloskop
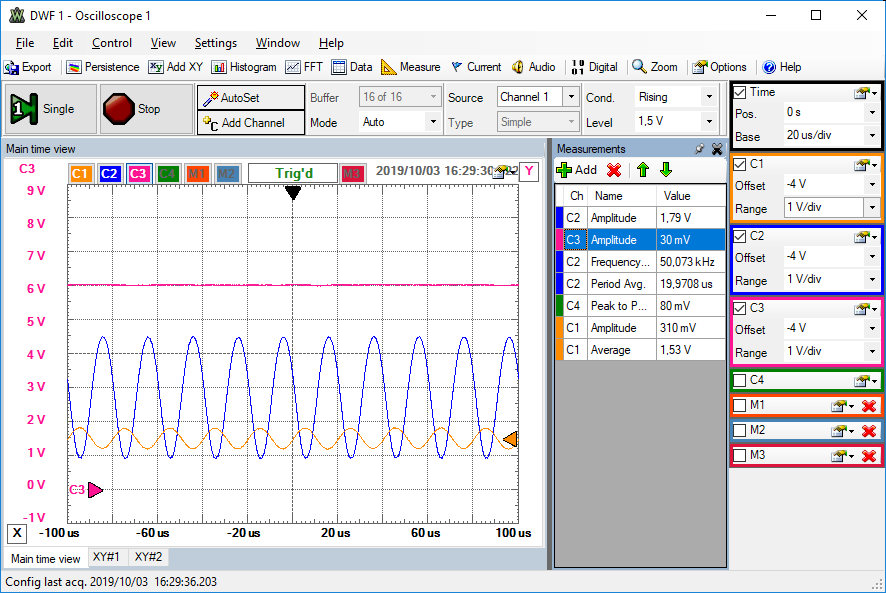
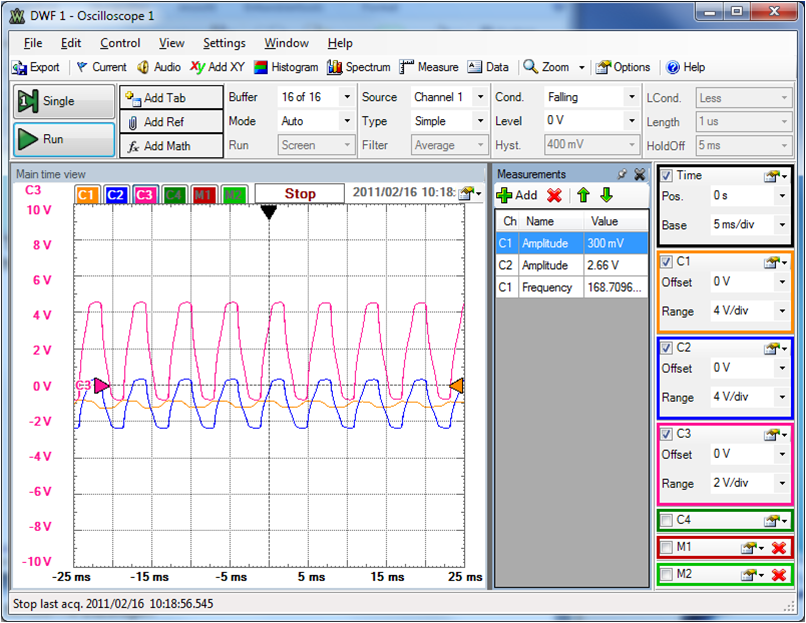
Hier wird ein Sinussignal dargestellt (blau, gelb).
Dazu gehört eine Gleichung:
\( u(t) = \hat{U} sin(\omega t) \)
ω ist die Kreisfrequenz in \( s^{-1} \).
Es gibt den Zusammenhang mit der Frequenz:
ω = 2 π f
Praxisbezug: Signalgenerator
|
Signalform Frequenz Amplitude Gleichanteil (Offset) Phase Duty Cyle (Symmetry) Drehregler |
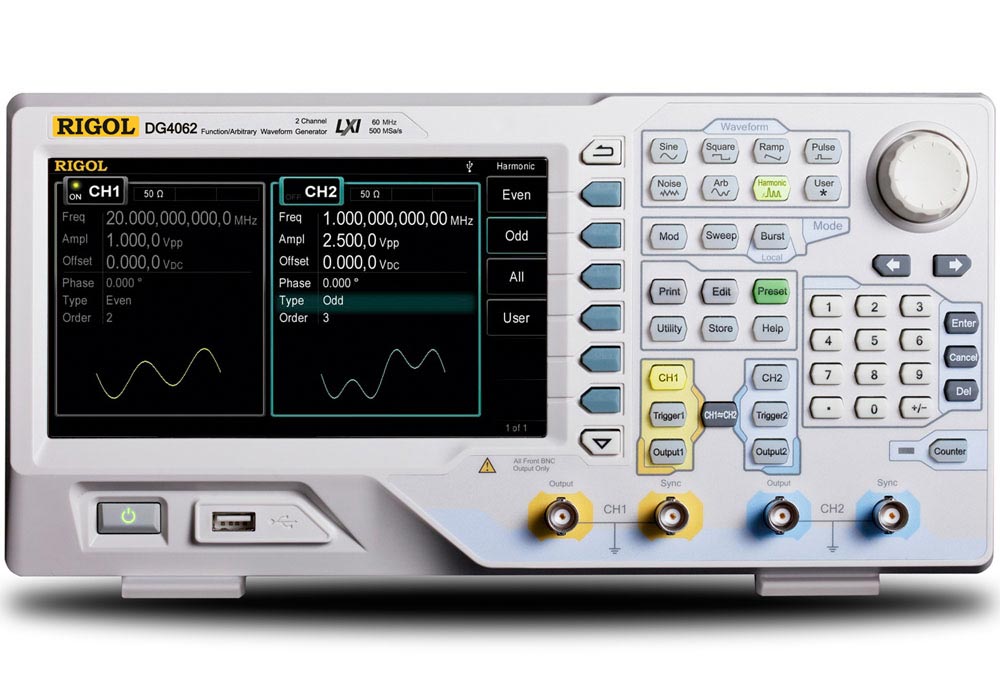 Signalgenerator Rigol |
|
Abbildung des Gerätes in Software Durch ein Screencopy kann man alle eingestellten Parameter sichern und dokumentieren. Damit ist es leichter eine Messung zu wiederholen und zu reproduzieren. Mögliche Fehleinstellungen werden sichtbar. |
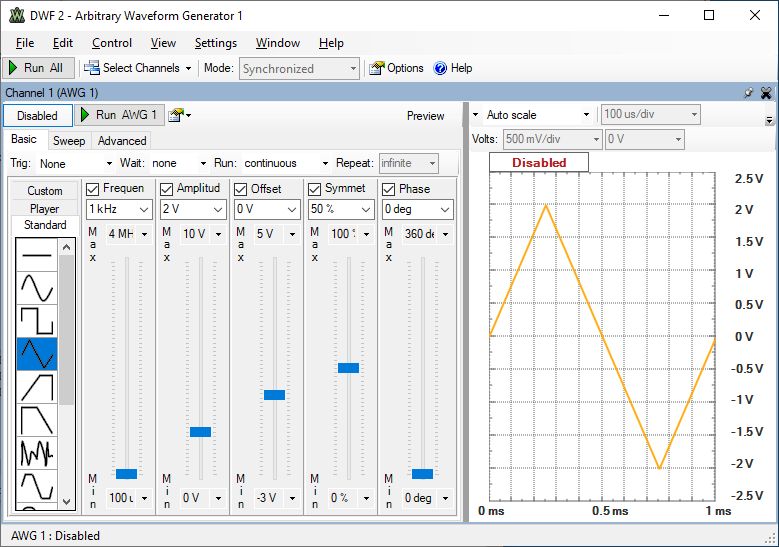 Signalgenerator Waveforms |
Periodische Schwingung
 |
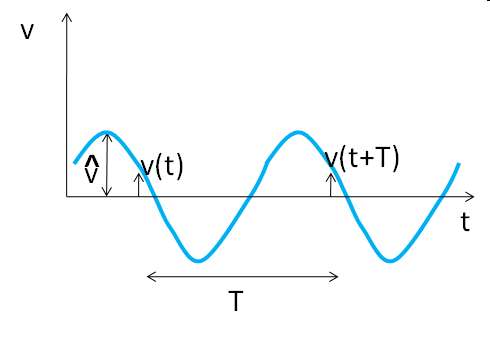Periodizitätv(t) = v(t +kT) k= 0,±1, ±2, ±3 |
|
SchwingungsbreiteSpitze Spitze Wert (peak-to-peak value) vpp = vmax - vmin |
Test 2
Geben Sie die Charakteristischen Größen der folgenden Spannungsmessung an:
Strommessung mit dem Oszilloskop
|
Der Spannungsabfall an einem Widerstand wird zur Strommessung verwendet. Der Strom wird dabei mit dem ohmschen Gesetz berechnet: \( I = \frac{U}{R_{mess}} \) |  | |
|
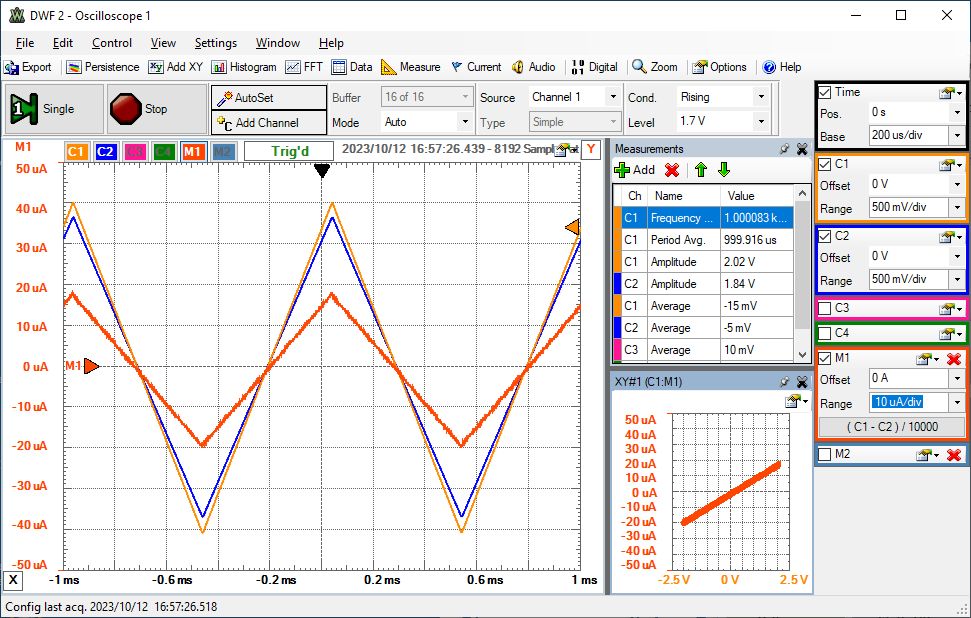
Eine Dreiecksspannung wird erzeugt. Die Spannungen am Messwiderstand werden mit 2 Messspitzen oder einer Differenzmessspitze gemessen. Mit einer Mathematikfunktion M1 = (C2 - C1) / RMESS wird der Strom dargestellt. Durch eine x-y Darstellung kann die Kennlinie angezeigt werden. |
| |
Man sieht links oben den Breadboardaufbau eines Spannungsteilers auf dem Electronic Explorer.
Rechts daneben ist der Schaltplan abgebildet.
Schaltplan und Aufbau stellen das mathematische Verhalten eines Spannungsteilers dar.
\( U_{C2DC} = U_{U1DC} \frac{R_2}{R_1 + R_2} \)
Dabei ist
\( U_{1DC} = V1 = U_{AWG1} \)
Darunter sieht man das Oszilloskopbild.
Man kann das Oszilloskopbild nur verstehen, wenn man die Messpunkte (Knoten) der dargestellten Signale kennt.
Dazu benötigt man den Aufbau und den Schaltplan. Der Schaltplan sollte geeignete Namen für Quellen, Bauteile, Spannungen und Ströme haben.
Strommessung
Der Strom kann mit der Spannungsdifferenz an R1 bestimmt werden.
\( I = \frac{U_{U1DC}-U_{U2DC}}{R_1}\)
Dabei wird ein Spannungspfeil vom Knoten U1DC nach U2DC und ein Strompfeil in der selben Richtung angenommen.
Diese sollte man in die Schaltung einzeichnen.
Ist der Messwiderstand R1 zu gross, ist die Spannungsdifferenz, der Spannungsabfall am Widerstand sehr gross und die Ausgangsspannungklein.
Ist der Messwiderstand R1 zu klein, ist die Spannungsdifferenz sehr klein und kaum messbar.
Der Messwiderstand muss für eine zu messende Schaltung optimiert werden.
Schaltplan, Breadboard und Oszilloskopkanäle
Signalgenerator(rot): ANALOG, AWG 1
Masseanschluss, GND, 0 V
Oszilloskop: SCOPE, 1, DC (C1DC)
Oszilloskop: SCOPE, 2, DC (C2DC)
Widerstandsreihenschaltung: 1 kΩ 10 kΩ