Elektronik

15 Diode

Prof. Dr. Jörg Vollrath

14 Schaltungsentwurf

Video der 22. Vorlesung 22.12.2020

Länge: 00:00:00

0:1:0 Diodenübersicht

0:2:46 Handtaschenlampe

0:5:50 Strom-Spannungskennlinie und Gleichung der Diode

0:13:50 Excel Diodenkennlinien

0:19:28 Serienwiderstand

0:25:8 SPICE Diodenmodell

0:30:8 LED blinkt im praktischen Aufbau

0:34:54 Bestimmung der Parameter, Strommessung mit Widerstand

0:36:33 Dreieckspannung

0:38:8 Oszilloskopbild

0:40:25 xy-Darstellung

0:43:18 Leuchtdiode als Beispiel

0:48:46 Strommesswiderstände

0:51:18 Diodenmesswerte zur Bestimmung von Diodenparametern

0:54:23 Arbeitsbereich und Gleichung

0:56:18 Sperrstrom und Sättigungsstrom

0:59:18 Exponentialbereich Berechnung von n

1:2:43 Berechnung Mathnotepad

1:4:14 Widerstandsbereich

1:5:44 2 Werte aus dem Exponentialbereich zur Bestimmung n, Is

1:11:54 Diodenschaltsymbole: Shottky, Zener, LED

1:13:18 Logarithmische Kennlinien verschiedener Dioden

1:16:56 Lineare Kennlinien und Durchbruch

Heute

Dioden Schaltsymbol und Ausführung
Kennlinie
Diodenparameter
Bestimmung der Diodenparameter
Diodensimulation
Gleichrichter und Diodenmessung

Praxisbeispiel: Dioden

Taschenlampe

2 Dioden
Gleichrichtung
Spannungsverdopplung

3 Leuchtdioden LED
Lichterzeugung

Quelle: Joerg Vollrath

Man sieht eine Handtaschenlampe (crank lamp). Dies ist ein typisches einfaches mechatronisches Gerät.
Ein mechanischer Hebel versetzt über eine Zahnradübersetzung und eine Fliehkraftkupplung einen Magneten in Rotation, der in einer Spule (Induktivität) eine Wechselspannung (AC, V1, sine) erzeugt (induziert).
Oben sieht man eine Vergrößerung der Platine mit den Leuchtdioden (mitte rot umrandet) und den Gleichrichterdioden (oben, unten rot umrandet).
Die Dioden dienen in der Taschenlampe zur Gleichrichtung des Wechselspannungssignals des Generators und zusammen mit der Kapazität C1 zur Spannungsverdoppelung.
Die Leuchtdioden erzeugen dann das Taschenlampenlicht.
Weiterhin kann man in grün noch einen Akku in der Taschenlampe sehen.
Im Schaltbild ist der Einschalter weg gelassen.

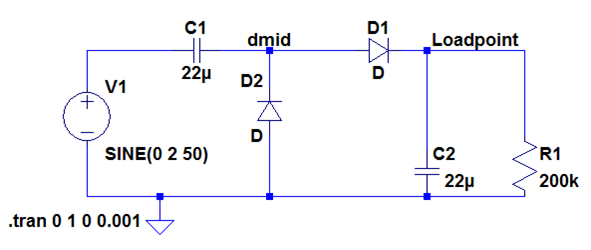
Strom-Spannungskennlinie der Diode

Diode_Symbol.asc

Version 4
SHEET 1 880 680
WIRE -32 48 -144 48
WIRE 144 48 32 48
SYMBOL diode 32 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D1
SYMATTR Value ""
TEXT 64 96 Left 2 !Anode
TEXT -144 96 Left 2 !Kathode
TEXT -16 -40 Left 2 ;U
TEXT -72 24 Left 2 ;I
LINE Normal -112 -16 -96 0
LINE Normal -96 -32 -112 -16
LINE Normal 96 -16 -112 -16
LINE Normal -96 48 -80 32
LINE Normal -80 64 -96 48

$I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

Vorwärtsbetrieb
Näherung für $\frac{U}{nU_T} \gt 1$ $I_D = I_S \left( e^{\frac{U}{nU_T}} \right)$
Temperaturspannung: $U_{T} = \frac{kT}{q} = 0.025 V$
für T=300K, Raumtemperatur
q = e = 1.6 · 10^-19 C
Elementarladung
k = 1.38 · 10^-23 J/K
Boltzmannkonstante
$10^{-18} A \lt I_S \lt 10^{-9} A$
Schleusenspannung oder Flussspannung
Darstellungen

Achsen linear

Strombereich für positive und negative Werte unterschiedlich

Stromachse logarithmisch

Stromwerte absolut
Kein Logarithmus einer negativen Zahl möglich
Ablesen des Exponenten

Quelle: Vollrath

Das Diodensymbol hat eine Anode und eine Kathode. Der Spannungspfeil geht von der Anode zur Kathode. Wenn an der Anode eine größere positive Spannung anliegt, fliesst ein Strom.
Um Schaltungen mit Dioden richtig zu berechnen und um die Herstellung einer Diode zu verbessern interessiert man sich für die Strom-Spannungs-Gleichung der Diode.
Man stellt eine exponentiellen Zusammenhang zwischen Strom und Spannung fest.
I_S und n hängen vom Material und dem Herstellungsprozess ab.
Anhand der Gleichung kann man auch eine Temperaturabhängigkeit von T sehen.
Auch der Strom I_S ist Temperaturabhängig.

Da die Gleichung sehr komplex ist, versucht man die Gleichung für Rechnungen durch Näherungen zu vereinfachen.

Die Gleichung ist rechts in verschiedenen Abbildungen dargestellt.
Die Grafik rechts oben hat für die positive x-Achse eine andere lineare Skalierung als die negative Achse, da die negativen Werte sehr klein sind.
In der Grafik unten wird der Absolutwert des Stromes logarithmisch aufgetragen.
Durch die positiven Werte kann man eine Gerade legen, wie man es von einer Exponentialfunktion erwartet.

SPICE Diodenmodell

.model Dx D(Is=2.52n Rs=.568 N=1.752)

.model 1N914 D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=20n Iave=200m Vpk=75 mfg=Motorola type=silicon)

DC Simulation

Is Saturation current
Rs Series Resistance
N Emission Coefficient
BV, IBV Breakdown voltage

AC, Transient Simulation

Cjo Zero bias junction capacitance
M Grading coefficient
Tt Transit time

Iave Current rating
Vpk Peak voltage rating
Type LED, zener, silicon, Shottky
Mfg Hersteller

$I_D = I_S\left( e^{\frac{q (U - I_D * R_S )}{nkT}}-1\right)$

DiodeModel.asc

Version 4
SHEET 1 880 680
WIRE 16 32 16 0
WIRE 144 112 16 112
WIRE 16 128 16 112
WIRE 144 144 144 112
WIRE 16 240 16 208
WIRE 144 240 144 208
WIRE 144 240 16 240
WIRE 16 272 16 240
SYMBOL res 0 16 R0
SYMATTR InstName RS
SYMATTR Value ""
SYMBOL current 16 128 R0
SYMATTR InstName BI
SYMATTR Value ID=F(VD)
SYMBOL cap 128 144 R0
WINDOW 0 -68 -52 Left 2
SYMATTR InstName C=Cj+CD
SYMATTR Value ""

Quelle: Vollrath

Zur Simulation benötigt man die elektrischen Parameter einer Diode.
Diese teilt man dem Simulationsprogram durch einen Text ('Edit','SPICE directive') mit.
Hier wird ein Modell einer Diode des Typs Dx und 1N914 dargestellt.
Die Diode Dx hat nur die wichtigsten Parameter Is, Rs, und n.
Für ein genaueres Modell fehlen Parameter für die default Werte eingesetzt werden.
Mit diesen berechnet SPICE das Strom-Spannungs-Verhalten.
Ein genaueres Modell mit mehr Parametern ist für die Diode 1N914 angegeben.

Bestimmung der Parameter der Diodengleichung

Es sollen von einer Diode Is, n und Rs bestimmt werden.

3 Unbekannte, 3 Gleichungen

Der Strom wird mit einem Widerstand gemessen.
Welche Widerstandswerte werden benötigt?

Das Spannungsmessgerät hat eine begrenzte Auflösung: 20mV
Die maximale Spannung der Spannungsversorgung beträgt 10V

$I = \frac{U}{R} = \frac{UOSC2 - UOSC1}{R1}$

R [ $\Omega$ ]	I_min	I_max
10
100
1k
1M

R [ $\Omega$ ]	I_min	I_max
10	2 mA	1 A
100	0.2 mA	100 mA
1k	20 $\mu$ A	10 mA
1M	20 nA	10 $\mu$ A

Man verwendet die minimale und maximale Spannung zur Bestimmung des Stroms.

DiodeR1.asc

Version 4
SHEET 1 1308 680
WIRE 176 80 80 80
WIRE 288 80 256 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 OSC1
FLAG 80 80 OSC2
SYMBOL voltage 80 112 R0
SYMATTR InstName V1
SYMATTR Value 1
SYMBOL res 272 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1
SYMATTR Value Dx
TEXT 64 296 Left 2 !.model Dx D(Is=10f Rs=0.0\n+ N=1.0 Cjo=0 M=0.5  tt=0  \n+Iave=200m Vpk=75 mfg=Motorola type=silicon)
TEXT 308 228 Left 2 !.dc V1 -1 1 0.01

1M

$\Omega$ ist der Eingangswiderstand des Multimeters/Oszilloskops.
Der Messwiderstand muss an den Strombereich angepasst werden.
Zur Messung sehr kleiner Ströme benötigt man sehr grosse Widerstandswerte.
Der sehr grosse Eingangswiderstand des Oszilloskops kann den Messstrom beeinflussen.

Beispiel: Diodenmessung

An einer idealen Diode mit einem Serienwiderstand RS werden folgende Messungen gemacht.

In welchen Arbeitsbereichen befindet sich die Diode bei den Messungen 1..4?
Bestimmen Sie näherungsweise Is, n und den Serienwiderstand RS. (UT=0.025V)

Messung	1	2	3	4
V_Diode	-2 V	0.5 V	1.4 V	1.6 V
I_Diode	-0.3 nA	11 uA	400 mA	600 mA
Arbeitsbereich

Messung 1:

$I_S = 0.3 nA$ Sättigungsstrom, Sperrstrom
Messung 2:

$I = I_S \left( e^{\frac{U}{n U_T}} \right)$

$n = \frac{U}{ U_T ln \left( \frac{I}{I_S} +1 \right)} = \frac{0.5 V}{ 0.025 V ln \left( \frac{11 \mu A}{0.3 nA} +1 \right)} = 1.9$
Messung 3 und 4:

$U_{Diode3} = n U_T ln \left( \frac{I}{I_S} + 1 \right)$

$= 1.9 \cdot 0.025 V ln \left( \frac{0.4}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_3 - U_{Diode3}}{I_3} = 1 \Omega$

$U_{Diode4} = 1.9 \cdot 0.025 V ln \left( \frac{0.6}{ 0.3 \cdot 10 ^{-9}} +1 \right) = 1 V$

$R_S = \frac{U_4 - U_{Diode4}}{I_4} = 0.97 \Omega$

$R_S = \frac{ \Delta U}{ \Delta I} = \frac{U_4 - U_3}{I_4 - I_3} = \frac{0.2 V}{200 mA} = 1 \Omega$
Wenn keine Messwerte für den Sperrstrom vorhanden sind, kann man eine Verhältnis von zwei Messungen im Durchlassbereich verwenden um n zu bestimmen:

$\frac{I_{1}}{I_{2}} = \frac{I_s e^{\frac{U_1}{n k T}}}{I_s e^{\frac{U_2}{n k T}}} = e^{\frac{U_1 - U_2}{n k T}}$
Mit n kann man dann für einen Messpunkt I_s bestimmen.

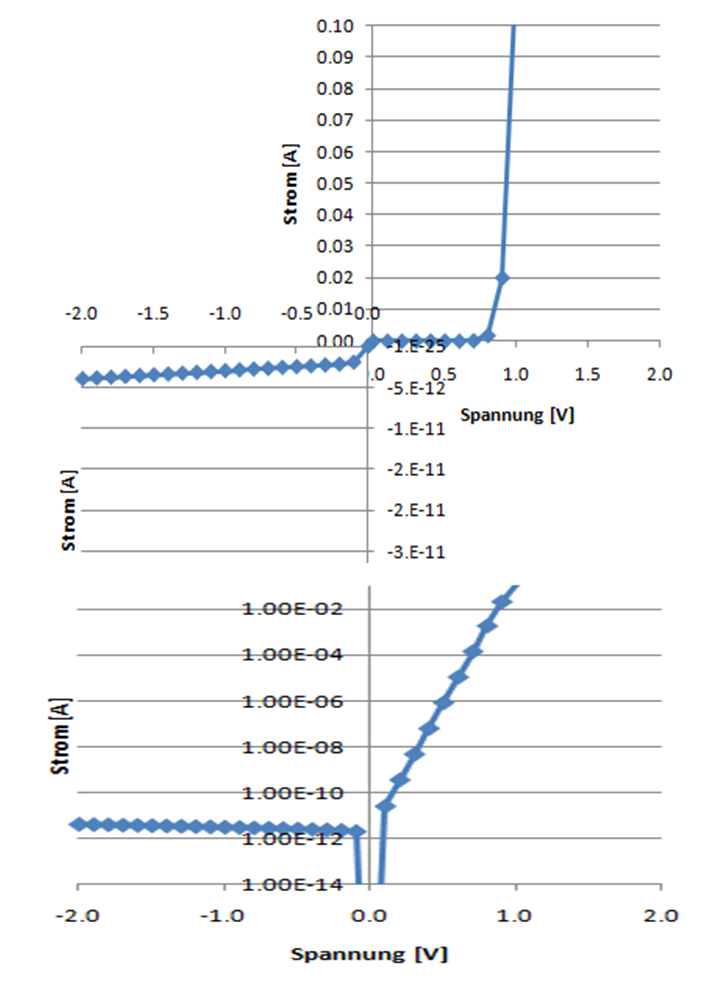
Diodenkennlinie

In der logarithmischen Darstellung sieht man 3 Bereiche.
Links den Sperrbreich der Strom ist näherungsweise konstant: I = I_s
In der Mitte der exponentielle Anstieg:

$I = I_S e^{\frac{U}{n U_T}}$
Rechts der Widerstandsbereich: dI = dU/R

Entsprechende Regressionsgleichungen (Trendlinien) sind im Graphen dargestellt.

x ist dabei die Diodenspannung, y ist der Diodenstrom.
Für sehr grosse Spannungen bestimmt man den inneren Serienwiderstand.
y = 1.1573 x - 1.1243

$R = \frac{d U}{d I} = \frac{d x}{d y} = \frac{1}{1.1573} \Omega = 0.86 \Omega$

Im Exponentialbereich bestimmt man Is und n. Der Strom ist so klein, dass der Spannungsabfall am Serienwiderstand vernachlässigbar ist.

$y = 3E-10e^{20.85x}$
Is = 3E-10

$\frac{1}{n U_T} = 20.85$

$n = \frac{1}{20.85 U_T} = 1.92$
Im Sperrbereich kann man den Strom Is bestimmen. Da dieser sehr klein ist, ist es sehr schwierig den Strom Is zu messen.

Excel Diodenkennlinie

Excel Arbeitsblatt Diodenkennlinie

Diodenkennlinie Messdatenfit

Diodensymbole (LTSPICE) und Gleichung

Vorwärtsbetrieb

$I_D = I_S \left( e^{\frac{q U}{n k T}} - 1 \right)$
Durchbruch

$U_D < BV$

$I_D = - I_S \left( e^{- \frac{q (U+BV)}{n k T}} - 1 + \frac{q BV}{k T} \right)$

Dioden_arten_01.asc

Version 4
SHEET 1 880 680
WIRE -288 -160 -336 -160
WIRE -144 -160 -288 -160
WIRE -288 -128 -288 -160
WIRE -144 -128 -144 -160
WIRE -288 -32 -288 -64
WIRE -144 -32 -144 -64
WIRE -288 16 -320 16
WIRE -128 16 -288 16
WIRE -288 32 -288 16
WIRE -128 32 -128 16
WIRE -288 128 -288 96
WIRE -128 128 -128 96
WIRE -288 160 -320 160
WIRE -128 160 -288 160
WIRE -128 176 -128 160
WIRE -288 192 -288 160
WIRE -288 272 -288 256
WIRE -128 272 -128 240
FLAG -336 -160 V1
FLAG -320 16 V1
FLAG -320 160 V1
FLAG -288 -32 0
FLAG -144 -32 0
FLAG -288 128 0
FLAG -128 128 0
FLAG -288 272 0
FLAG -128 272 0
SYMBOL diode -304 -128 R0
WINDOW 0 38 19 Left 2
WINDOW 3 42 47 Left 2
SYMATTR InstName D_Silicon
SYMATTR Value 1N914
SYMBOL schottky -160 -128 R0
WINDOW 0 50 17 Left 2
WINDOW 3 47 46 Left 2
SYMATTR InstName D_Shottky
SYMATTR Value MBR0520L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL zener -304 32 R0
WINDOW 0 41 21 Left 2
WINDOW 3 38 52 Left 2
SYMATTR InstName D_Zener
SYMATTR Value BZX84C10L
SYMATTR Description Diode
SYMATTR Type diode
SYMBOL diode -144 32 R0
WINDOW 0 48 12 Left 2
WINDOW 3 46 46 Left 2
SYMATTR InstName D_SiC
SYMATTR Value UPSC600
SYMBOL varactor -304 192 R0
WINDOW 0 39 21 Left 2
WINDOW 3 44 57 Left 2
SYMATTR InstName D_varactor
SYMATTR Value MV2201
SYMATTR Type diode
SYMBOL LED -144 176 R0
WINDOW 0 83 8 Left 2
WINDOW 3 85 42 Left 2
SYMATTR InstName D_LED
SYMATTR Value NSCW100
SYMATTR Description Diode
SYMATTR Type diode
TEXT -112 0 Left 2 !.dc V1 -2 4 0.1
TEXT -96 136 Left 2 !V1 V1 0 DC 1

Quelle: Vollrath

Auch eine Solarzelle ist eine Diode.

Im Schaltplan sind verschiedene Diodenarten abgebildet.
Eine Siliziumdiode, eine Shottkydiode, eine Zenerdiode, eine Siliziumkarbitdiode, eine Varactordiode und eine LED.
Diese haben sehr verschiedene Diodenparameter.

Im Sperrbereich gibt es eine Maximalspannung, bis zu der die Diode noch sperrt.
Diese Spannung bezeichnet man als Durchbruchsspannung.
Für diesen Bereich kann man die Diodengleichung erweitern.

Dioden in LTSPICE

Netzliste (netlist)
D_Silicon N001 0 1N914
D_Shottky N001 0 MBR0520L
D_Zener N001 0 BZX84C10L
D_SiC N001 0 UPSC600
D_varactor N001 0 MV2201
D_LED N001 0 NSCW100
V1 N001 0 1
.model D D
.lib c:\lib\cmp\standard.dio
.dc V1 -2 4 0.1
.backanno
.end
Dioden fangen in der Netzliste mit dem Buchstaben D an.
Es gibt eine Bibliothek (library) standard.dio mit Bauteileigenschaften.

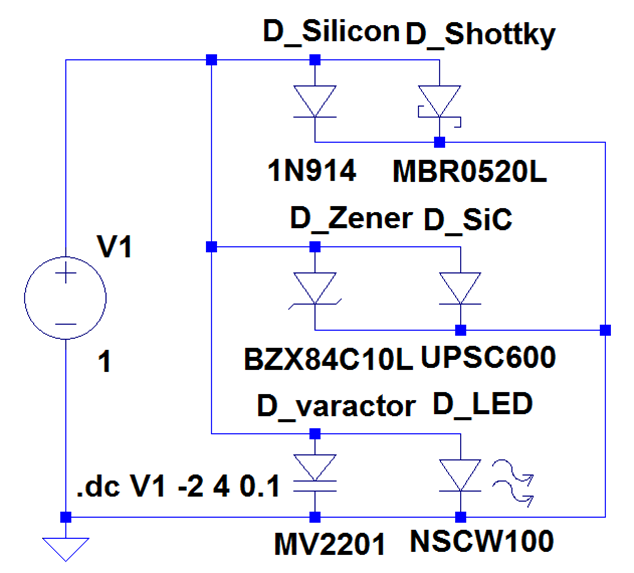Quelle: Vollrath

Dioden Kennlinie logarithmisch in LTSPICE

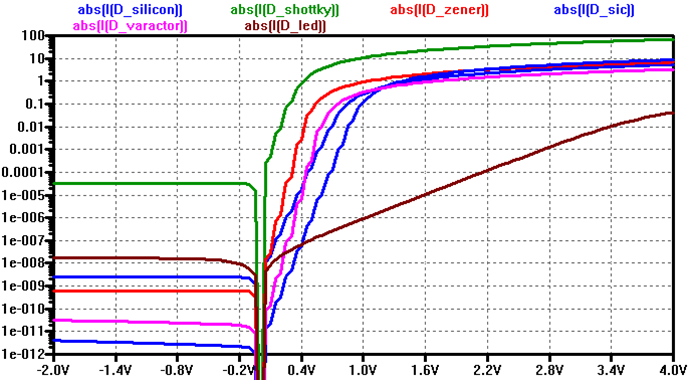
Quelle: Vollrath

	Silizium	Shottky	Zener	SiC	Varaktor	LED
I_s (A)	2.25n	31.7u	0.6n	2p	1.36p	16.9n
n	1.752	0.78	1	1.5	1	6.79
Rs (Ohm)	0.568	0.115	0.5	0.33	1	8.163

Dioden Kennlinie linear in LTSPICE

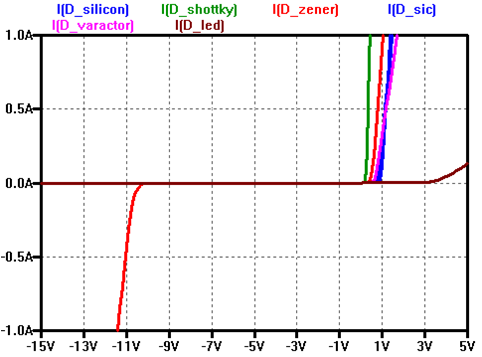
Quelle: Vollrath

Bei der Zenerdiode sieht man bei -10 V Sperrspannung einen Durchbruch, der Strom steigt an.
Zenerdioden sind für verschiedene Spannungen zur Spannungsstabilisierung erhältlich.
Die meisten Dioden haben eine Flussspannung um die 0.7 V. Nur die LED hat eine Flusspannung oberhalb von 3 V.

Ersatzschaltbilder

Warum benötigt man Ersatzschaltbilder?
Was sind Ersatzschaltbilder?
Wie kann man Ersatzschaltbilder klassifizieren?

Ein elektrisches Bauteil wird mit Hilfe von linearen Elementen: gesteuerten Quellen, Schaltern, Widerständen, Kapazitäten und Induktivitäten modelliert.
Schaltungen mit linearen Bauelementen kann man berechnen.

Kleinsignalersatzschaltbild

Was passiert bei kleinen Spannungs oder Stromänderungen um einen festen Arbeitspunkt?
Diodenspannung 1V
überlagertes Signal 10mV

Großsignalersatzschaltbild

Wie kann man die Diodengleichung durch ideale Bauteile annähern?

Ersatzschaltbild und Kleinsignalverhalten

Ein Widerstand R = 10

$\Omega$ und eine Diode sind in Reihe an einer Spannungsquelle V1 = 1 V angeschlossen.
Der Strom I soll berechnet werden?

$I = I_S\left( e^{\frac{q (V_1 - I * R )}{nkT}}-1\right)$
Dies ist eine nichtlineare Gleichung.
Die Lösung der Gleichung kann nur iterativ durch Ausprobieren erfolgen.

Näherungslösungen:

Grosssignalberechnung
Kleinsignalberechnung

Diode_Messaufbau.asc

Version 4
SHEET 1 880 680
WIRE 144 80 80 80
WIRE 288 80 224 80
WIRE 288 112 288 80
WIRE 80 128 80 80
WIRE 80 240 80 208
WIRE 176 240 80 240
WIRE 288 240 288 176
WIRE 288 240 176 240
WIRE 176 256 176 240
FLAG 176 256 0
FLAG 288 80 SCOPE1DC
FLAG 80 80 SCOPE2DC
SYMBOL voltage 80 112 R0
SYMATTR InstName VAWG1
SYMATTR Value 1
SYMBOL res 240 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL diode 272 112 R0
SYMATTR InstName D1
SYMATTR Value 1N914
TEXT 40 296 Left 2 !.dc VAWG1 0.2 1.0 0.05

Berechnung einer Diodenschaltung: Graphische Lösung

Graphische Lösung:

Was passiert wenn nur die Diode vorhanden wäre?
Wie groß ist der Strom durch den Widerstand bei verschiedenen Diodenspannungen?
Widerstandslastkennline
Wenn 0V an der Diode anliegt fliesst der maximale Strom

$I = \frac{1 V}{ 10 \Omega} = 100 mA$ .
Wenn 1V an der Diode anliegt fliesst kein Strom I = 0.
Zwischen diesen 2 Punkten ist die Kennlinie linear, da der Widerstand ein lineares Bauelement ist. Das Ohmsche Gesetz gilt.

Man kann nun den Arbeitspunkt der Schaltung aus dem Schnittpunkt der Kurven bestimmen.

$U_{Diode} = 0.75 V$ und

$I = 25 mA$

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Die Diodenkennlinie ist sehr steil.
Was passiert, wenn als Diodenspannung 0.7 V angenommen wird?
Dies entspricht einer Spannungsquelle von 0.7 V.

Diodenspannung	Strom
0.7 V	20 mA
0.75 V	25 mA
0.8 V	30 mA

Die Abweichungen zur graphischen Lösung sind gering.
Je größer die Spannung und der Widerstand sind, desto geringer ist die Abweichung.

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Was passiert mit dem Strom, wenn sich die Spannung V1 geringfügig ändert?

Man ersetzt die nichtlineare Diodenkennlinie durch eine Tangente im Arbeitspunkt.
Man ersetzt die Diode durch einen Widerstand.

$r_D = \frac{ \Delta U}{ \Delta I} = \frac{1}{\frac{\delta I}{ \delta U}} = \frac{1}{\frac{\delta I_S \left( e^{\frac{U}{n U_T}} -1 \right)}{ \delta U}}$

$r_D = \frac{1}{\frac{ I_S \left( e^{\frac{U}{n U_T}}\right)}{ n U_T}} = \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}}\right) }$

$r_D \approx \frac{ n U_T}{I_S \left( e^{\frac{U}{n U_T}} - 1 \right) } = \frac{n U_T}{I_{Diode}} = 1 \Omega$

Man kann nun die Stromänderung der Schaltung im Arbeitspunkt mit der Spannungsteilerregel bestimmen.

$\Delta I = \Delta U \cdot \frac{ r_D}{ R + r_D}$

$\Delta I = 0.2 V \cdot \frac{ 1 \Omega }{ 10 \Omega + 1 \Omega} =0.018 mA$

Ersatzschaltbilder

Grosssignalersatzschaltbild:

Diode_GESB.asc

Version 4
SHEET 1 880 680
WIRE 48 144 0 144
WIRE 128 144 96 144
WIRE 224 144 208 144
SYMBOL voltage 112 144 R270
WINDOW 0 32 56 VTop 2
WINDOW 3 -32 56 VBottom 2
SYMATTR InstName V1
SYMATTR Value 0.7 V
LINE Normal 96 144 48 112

Schalter mit Spannungsquelle (0.7 V)

In Durchlassrichtung Kleinsignalersatzschaltbild:

Diode_KESB.asc

Version 4
SHEET 1 880 680
WIRE 336 144 304 144
WIRE 448 144 416 144
SYMBOL res 432 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RD
SYMATTR Value ""

Widerstand

$r_D \approx \frac{n U_T}{I_{Diode}}$

Diodenmessung

DiodeAn.asc

Version 4
SHEET 1 880 680
WIRE 64 48 32 48
WIRE 224 48 144 48
WIRE 32 80 32 48
WIRE 224 80 224 48
WIRE 32 176 32 160
WIRE 224 176 224 144
WIRE 80 240 32 240
WIRE 224 240 144 240
WIRE 224 272 224 240
WIRE 224 368 224 352
FLAG 224 176 0
FLAG 32 176 0
FLAG 32 48 C1
FLAG 224 48 C2
FLAG 224 368 0
FLAG 32 240 C1
FLAG 224 240 C3
SYMBOL res 160 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL diode 208 80 R0
SYMATTR InstName D1
SYMATTR Value 1N914
SYMBOL voltage 32 64 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value SINE(0 3 1k)
SYMBOL res 240 368 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName R2
SYMATTR Value 1k
SYMBOL diode 80 256 R270
WINDOW 0 32 32 VTop 2
WINDOW 3 0 32 VBottom 2
SYMATTR InstName D2
SYMATTR Value 1N914
TEXT 174 408 Left 2 !.tran 1m

Schaltung zur Diodenkennlinie
Schaltung zur Durchlass- und Sperrrichtung

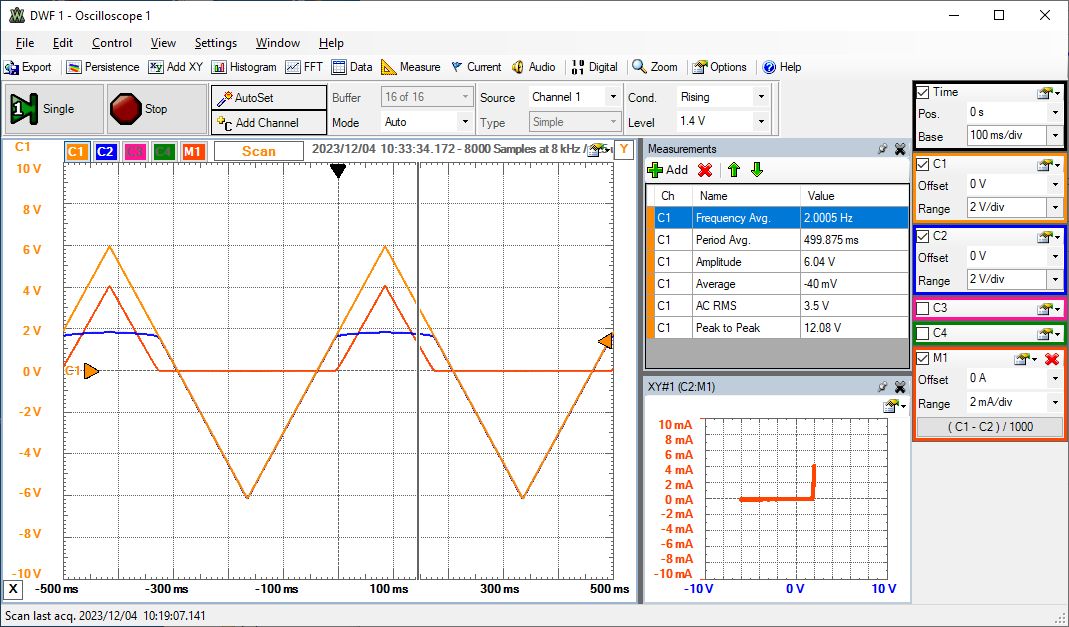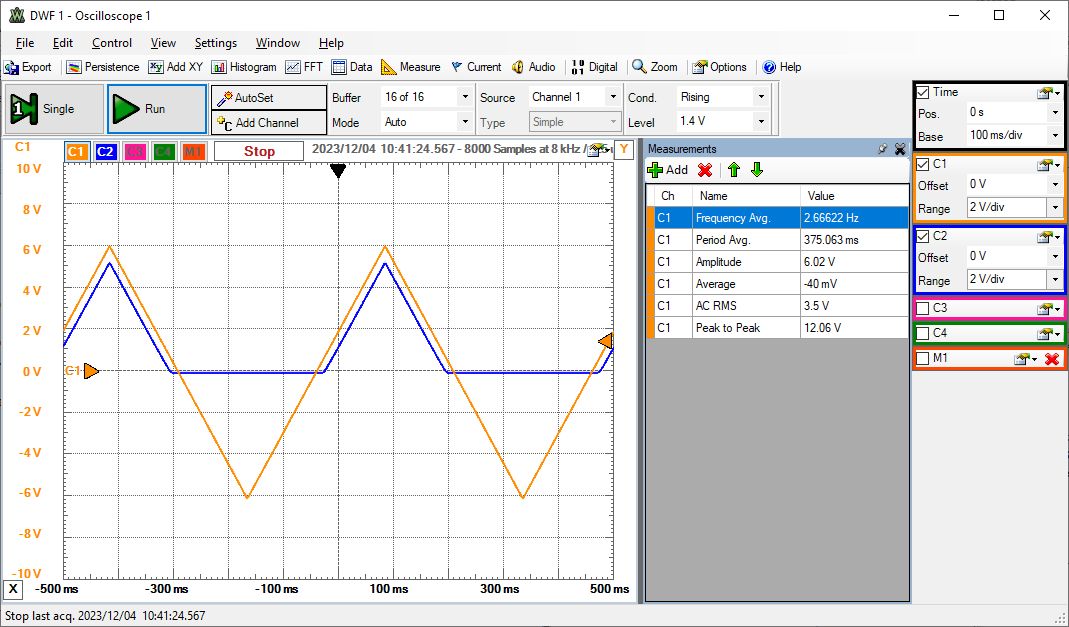Diodenkennlinie

Das Oszilloskopbild (rechts oben) der Spannungen an einer Reihenschaltung von Widerstand und Diode zeigt eine Dreiecksform der Spannung des Generators AWG1(C1 orange).
Die blaue Kurve C2 zeigt die Spannung an der Diode. Sobald eine Strom fliesst, bleibt die Spannung an der Diode nahezu konstant.
Der Strom wird als Differenz (C1 - C2) / 1000 für den 1000 Ω Messwiderstand berechnet und erreicht maximal 4 mA.
Die Diodenkennlinie kann man als xy Darstellung im kleinen Fenster sehen.

Durchlass- und Sperrverhalten

In dieser Schaltung ist die Reihenfolge von Widerstand und Diode vertauscht.
Man sieht wieder die Eingangsspannung (C1, orange) und die Spannung zwischen Diode und Widerstand.
Die Eingangsspannung wird in Durchlassrichtung um eine Diodenspannung verringert. Bei negativen Eingangsspannungen sperrt die Diode und am Widerstand liegen Null Volt an.
Man spricht von einer Gleichrichtung der Eingangsspannung.
Diese Schaltung wird benutzt, um aus einer Wechselspannung eine Gleichspannung zu erzeugen.
Ein Kondensator parallel zum Widerstand kann das Pulsieren der Ausgangsspannung verkleinern.

Temperaturverhalten der Diode

Sperrstrom und Durchlassstrom steigen mit der Temperatur.

$I_D = I_S \left( e^{\frac{U}{nU_T}} -1 \right)$

$I_S \sim B·T^3·exp^{-\frac{W_g}{kT}}$

$U_T \sim T$

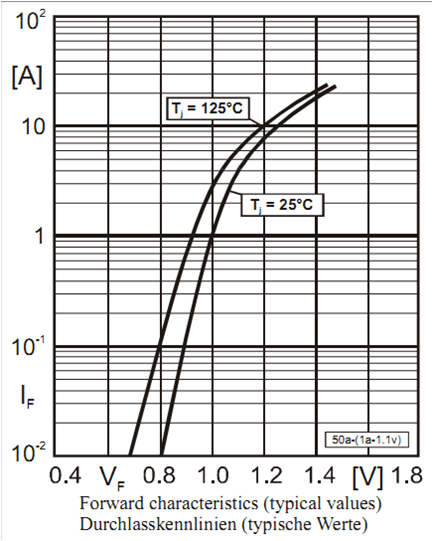Quelle: Datenblatt

Beim automatischen Testen von integrierten Schaltkreisen könen die Schutzdioden an den Pins zur Messung der Testtemperatur benutzt werden. Bei einem konstanten Strom wird die Spannung gemessen.
Dadurch wird sichergestellt, dass man wirklich die Solltemperatur für den Test erreicht hat.

Diodengleichungen

Symbol

Diode_Symbol.asc

Diodenstrom

$I_D = I_S\left( e^{\frac{q U - I_D R_S}{nkT}}-1\right)$

ohne Serienwiderstand:

$I_D = I_S\left( e^{\frac{q U}{nkT}}-1\right)$

in Flussrichtung U >> U_T:

$I_D = I_S e^{\frac{q U}{nkT}}$

in Sperrrichtung U < 0:

$I_D = - I_S$

Temperaturspannung

$U_T = \frac{kT}{q}$

$U_T(RT = 300 K = 27 °C) = 25mV$

Lernziele

Sie kennen die Strom-Spannungs-Diodengleichung und ihre Parameter.
Sie können eine Diode simulieren und messen.
Sie können aus Simulationsdaten oder Messdaten die Diodenparameter bestimmen.
Sie können mit einem Ersatzschaltbild einer Diode Spannungen und Ströme berechnen.
Sie können eine Diode als Gleichrichter verwenden.

Auch eine Solarzelle ist eine Diode.

Nächste Vorlesung:

Was ist ein MOSFET?
Bauteilparameter
Strom, Spannungskennlinie
MOSFET als Schalter und Verstärker

16 MOSFET

2024 11 25 15 Diode Elektronik Prof. Dr. Joerg Vollrath

Elektronik

15 Diode

Prof. Dr. Jörg Vollrath

Video der 22. Vorlesung 22.12.2020

Heute

Praxisbeispiel: Dioden

Strom-Spannungskennlinie der Diode

SPICE Diodenmodell

Bestimmung der Parameter der Diodengleichung

Beispiel: Diodenmessung

Diodenkennlinie

Diodensymbole (LTSPICE) und Gleichung

Dioden in LTSPICE

Dioden Kennlinie logarithmisch in LTSPICE

Dioden Kennlinie linear in LTSPICE

Ersatzschaltbilder

Ersatzschaltbild und Kleinsignalverhalten

Berechnung einer Diodenschaltung: Graphische Lösung

Berechnung einer Diodenschaltung: Grosssignalersatzschaltbild

Grosssignalersatzschaltbild und Rechnung.

Berechnung einer Diodenschaltung: Kleinsignalersatzschaltbild

Ersatzschaltbilder

Diodenmessung

Diodenkennlinie

Durchlass- und Sperrverhalten

Temperaturverhalten der Diode

Diodengleichungen

Lernziele

Nächste Vorlesung: